A huszadik század elején a Göttingeni Egyetem a világ egyik legjobb matematikai kutatóközpontja volt. A matematikus David Hilbert elismert professzor volt ott, és 1924-25 téli félévében előadássorozatot tartott a matematikában, fizikában és csillagászatban a végtelenről. (Ezek és Hilbert más előadásai ma már könyv formájában is megjelentek a Springer-Verlag kiadónál. A könyv az IAS könyvtárában fordításban és eredeti német nyelven is elérhető). Az egyik ilyen előadásban egy példán keresztül magyarázta el a véges és a végtelen halmazok közötti döntő különbséget: egy véges számú szobával rendelkező szállodában, ha minden szoba foglalt, akkor nincs hely új vendégek számára. Egy végtelen sok szobával rendelkező szállodában azonban ez nem jelent problémát: ha minden szoba foglalt, és új vendég érkezik, egyszerűen minden régi vendéget áthelyezünk egy szobával arrébb, és az első szoba üresen marad az újonnan érkező vendég számára. Hasonló érvvel bármilyen véges számú, sőt végtelen sok újonnan érkező vendéget el tudunk helyezni.”

George Gamow (a fizikai kozmológia területén híres Alpher-Bethe-Gamow-dolgozat szerzője) néhány évvel ezen előadások után nyári posztdoktorandusz volt a Göttingeni Egyetemen, és valószínűleg ott ismerte meg Hilbert példáját a végtelen szállodáról. Ő népszerűsítette azt 1947-ben megjelent, Egy kettő három… végtelen című népszerű tudományos könyvében: Facts and Speculations of Science (elérhető a Princeton University könyvtárában).

Kanyarodjunk vissza Hilbert szállodájához. A rend kedvéért mondjuk, hogy a szálloda végtelen sok szobája az 1, 2, 3, 4, 5, . . . számozott. Egyik este mindegyik foglalt, de érkezik egy új vendég. Mint már mondtuk, az 1-es szobában lévő vendéget egyszerűen áthelyezzük a 2-es szobába, a 2-es szobában lévőt a 3-as szobába, a 3-as szobában lévőt a 4-es szobába, és általában az n-es szobában lévő vendéget az n+1-es szobába, így az 1-es szobában üres hely keletkezik az új vendég számára, de az eredeti vendégek egyike sem marad hajléktalan.

Tegyük fel, hogy nem csak egy, hanem húsz új vendég érkezik. A korábban használt trükk ugyanúgy működik: az 1-es szobában lévő vendéget helyezzük át a 21-es szobába, a 2-es szobában lévő vendéget a 22-es szobába, és általában az n-es szobában lévő vendéget az n + 20-as szobába. Így húsz szoba marad üresen és készen áll a húsz új vendég számára.

De mi van akkor, ha végtelen sok új vendég érkezik egy végtelen buszon? Módosíthatjuk az előző érvelést úgy, hogy az ebben a helyzetben is működjön: osszuk el a már a szállodában lévő vendégeket úgy, hogy csak minden második szobát foglalják el. Matematikailag fogalmazva: az n-es szobában lévő vendéget helyezzük át a 2n-es szobába, így az összes páros számú szoba foglalt lesz. Így minden más szoba (végtelen sok!) üresen marad, és készen áll a busszal érkező (végtelen sok!) ember befogadására. A buszon az n-es számú ülésen ülő személynek az n-edik páratlan számú szobába kell költöznie, ami a 2n-1-es számú szoba.

Mi van, ha kilencvenkilenc végtelen számú busz érkezik? Egyszerűen helyezzük át az eredeti szállóvendégeket a 100, 200, 300 stb. szobába, az első busz utasait az 1, 101, 201 stb. szobába, a második busz utasait a 2, 102, 202 stb. szobába, és így tovább a többi busz esetében. Ez a szálloda összes szobáját elfoglalja, miközben egyetlen vendég sem marad szoba nélkül. Ha a buszok utasai maguk is az 1, 2, 3, 4, 5, … számmal lennének ellátva. (és ne tegyünk különbséget, és nevezzük a szálloda eredeti vendégeit is utasoknak – gondolhatunk arra, hogy az összes eredeti vendéget kiköltöztetjük a szállodából egy közvetlenül a szálloda előtt parkoló díszes buszba, amelyet nevezhetünk 0. számú busznak), akkor azt látnánk, hogy a szálloda első száz szobáját az 1-es számú utasok töltik meg, a szálloda második száz szobáját a 2-es számú utasok, és így tovább.

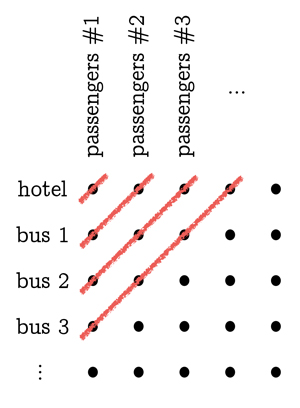
A következő szinten végtelen sok végtelen busszal kell foglalkozni (minden busz végtelen sok utassal). Az első teendő, hogy a szállodából és a buszokból mindenkit kiviszünk, és a parkolóban, vagy egy papírlapon rácsszerű alakzatba rendezünk: a szálloda eredeti vendégei (vagyis a 0. busz utasai) sorakozzanak fel, balról jobbra, egy sort alkotva. Az első busz utasai alkossanak egy másik sort közvetlenül alatta, a második busz utasai pedig egy sorral alatta, stb. A sorokat úgy állítsuk egymás mellé, hogy az egyes buszok 1-es számú utasai egy oszlopban sorakozzanak fel, a 2-es számú utasok az attól jobbra lévő oszlopban, és így tovább. Ha most elkezdjük feltölteni az 1-es, 2-es, 3-as, 4-es, … szállodai szobákat az első sorból érkező emberekkel, soha nem fogjuk befejezni, és továbblépünk a második sorba, és ugyanígy, ha az első oszloppal próbáljuk kezdeni. A trükk az, hogy átlós vonalakra kell gondolni, amelyek a rácson balról balra lentről jobbra fentre futnak. Ezen átlós vonalak közül a legbal oldali csak egy bal felső személyt érint (0. busz, 1. utas): ezt a személyt az 1. szobába tesszük. A következő átlós vonal két személyt érint (1. busz, 1. utas és 0. busz, 2. utas): ezt a két személyt a 2. és 3. szobába tesszük. A következő átlós vonal három személyt érint: helyezzük őket a következő három üres szobába, a 4, 5, 6-osba. Ezt a mintát folytatva végül a parkolóban türelmesen ácsorgó emberek mindegyikéhez rendelünk egy-egy szobát.

Mélyebbre mehetünk a végtelenbe, mélyebbre, mint a végtelen sok végtelen busz? Igen, tudunk: képzeljük el, hogy Hilbert szállodája mellett közvetlenül egy parkolóház van. Az első emeleten, közvetlenül a szálloda ajtaja mellett áll a már ismert végtelen sok végtelen buszunk. De aztán észrevesszük: a garázsnak végtelen sok emelete van, mindegyikben végtelen sok végtelen busz. Meg tud-e birkózni a Hilbert-hotel a végtelenségnek ezzel a plusz rétegével? A válasz igen! Elképzelhetjük, hogy az előző módszerrel a parkolóház minden emeletén egyetlen utascsoportot hozunk létre, majd minden egyes utascsoportnak azt mondjuk, hogy szálljon be egy-egy végtelen buszba. Most visszavezettük a problémát végtelen sok végtelen buszra, amelyekről tudjuk, hogy elférnek a szállodában.

Mi van, ha a végtelenség egy újabb rétegét adjuk hozzá? Például, ha végtelen sok parkolóház van, mindegyikben végtelen sok emelet, minden emeleten végtelen sok busz, minden buszban végtelen sok utas? Ez a végtelenség négy rétege, és a válasz még mindig igen! Sőt, a válasz még a végtelenség négyezer rétegére is igen. Megáll valaha is? Hilbert szállodája valaha nem tud újabb vendégeket fogadni? Van olyan végtelen, ami túl nagy Hilbert szállodája számára?

Igen, van. Valóban, ha a végtelenségnek végtelen sok rétege lenne, akkor az összes embert nem lehetne Hilbert szállodájában elhelyezni. Akkor …mi történik? Kiderül, hogy az összes leírt végtelenség, egészen az utolsóig, ugyanolyan méretű. Ezt a méretet ℵ0-nak (alef nulla) nevezzük, ez a ℕ = {1, 2, 3, 4, …} halmaz mérete, és az, hogy hány szoba van Hilbert szállodájában. Georg Cantor volt az, aki 1874-ben bevezette azt a gondolatot, hogy hogyan lehet összehasonlítani a végtelen mennyiségek méretét, és megmutatta, hogy léteznek különböző méretű végtelen mennyiségek. Több jelentős matematikus (Poincaré, Kronecker, később Weyl) határozottan ellenezte elképzeléseit, akárcsak néhány teológus – ők azt állították, hogy Cantor elképzelései megkérdőjelezik Isten abszolút végtelenségének egyediségét. Hilbert viszont támogatta és védelmezte Cantort.

A végtelen halmazok méretének összehasonlítása nem sokban különbözik a véges halmazok méretének összehasonlításától: ahhoz, hogy megtudjuk, több szék vagy több ember van-e egy előadóteremben, nem kell megszámolni az embereket és a székeket, és összehasonlítani a két számot. Elég egy pillantást vetni a teremre, és megnézni, hogy vannak-e üres székek (több szék, mint ember) vagy állva maradt emberek (több ember, mint szék): ha minden egyes ember egy székben ül, és nincsenek üres székek, akkor a székek halmaza és az emberek halmaza azonos méretű. Hasonlóképpen, ha a buszokon minden utas kap egy szobát Hilbert szállodájában, és egyetlen szoba sem marad üresen, akkor az utasok halmaza ugyanolyan méretű végtelen, mint Hilbert szállodájában a szobák halmaza, ℵ0. Cantor ezt a gondolatot arra használta, hogy megmutassa, hogy a valós számok halmaza, ℝ, szigorúan nagyobb, mint a természetes számok halmaza, ℕ; gyönyörű érvelése “Cantor átlója” néven vált ismertté. Cantor azt is feltételezte – és megpróbálta bizonyítani, de nem sikerült -, hogy létezik a kontinuus hipotézis: nincs olyan végtelen halmaz, amely szigorúan nagyobb, mint ℕ, de szigorúan kisebb, mint ℝ. Hilbert annak bizonyítását, hogy ez az állítás igaz vagy hamis, első problémaként szerepeltette azon a híres huszonhárom problémából álló listán, amelyet az 1900-as párizsi Nemzetközi Matematikus Kongresszuson mutatott be, és amely a következő évtizedekre meghatározta a matematikai kutatások irányát. A válasz az, hogy ez a hipotézis nem bizonyítható hamisnak (Gödel, 1940-es évek), de azt sem lehet bizonyítani, hogy igaz (Cohen, 1960-as évek): ez egy eldönthetetlen probléma!”

Hilbert híres mondása Cantor végtelenséggel kapcsolatos elképzeléseiről és mindarról az új matematikáról, amit ezek hoztak: “Senki sem űzhet ki minket abból a paradicsomból, amelyet Cantor teremtett.”