A principios del siglo XX, la Universidad de Gotinga era uno de los principales centros de investigación matemática del mundo. El matemático David Hilbert era un profesor consolidado allí, y durante el semestre de invierno de 1924-25 dio una serie de conferencias sobre el infinito en matemáticas, física y astronomía. (Estas y otras conferencias de Hilbert han sido publicadas en forma de libro por Springer-Verlag. El libro está disponible en la biblioteca del IAS en traducción y en el original alemán). En una de estas conferencias, utilizó un ejemplo para explicar la diferencia crucial entre los conjuntos finitos e infinitos: en un hotel con un número finito de habitaciones, si todas las habitaciones están ocupadas, no hay espacio para nuevos huéspedes. Pero en un hotel con un número infinito de habitaciones esto no es un problema: si todas las habitaciones están ocupadas y llega un nuevo huésped, basta con trasladar a cada uno de los antiguos huéspedes una habitación más allá, dejando la primera habitación libre para el huésped recién llegado. Un argumento similar nos permite acomodar cualquier número finito, e incluso infinito, de huéspedes recién llegados.

George Gamow (del famoso artículo de Alpher-Bethe-Gamow en el campo de la cosmología física) fue un postdoc de verano en la Universidad de Göttingen unos años después de que ocurrieran estas conferencias y probablemente conoció allí el ejemplo de Hilbert del hotel infinito. Lo popularizó en su libro de divulgación científica de 1947, titulado One Two Three…Infinity: Facts and Speculations of Science (disponible en la biblioteca de la Universidad de Princeton).

Volvamos al hotel de Hilbert. Para hacer las cosas más claras, digamos que las infinitas habitaciones del hotel están numeradas 1, 2, 3, 4, 5, … . Una noche, todas están ocupadas pero llega un nuevo huésped. Como dijimos antes, simplemente trasladamos el huésped de la habitación 1 a la 2, el de la 2 a la 3, el de la 3 a la 4 y, en general, el de la habitación n a la n + 1, creando así una vacante en la habitación 1 para el nuevo huésped, pero sin dejar a ninguno de los huéspedes originales sin hogar.

Digamos ahora que llegan veinte nuevos huéspedes en lugar de uno solo. El truco utilizado antes funciona igual de bien: trasladar el huésped de la habitación 1 a la 21, el de la 2 a la 22 y, en general, el de la n a la n + 20. Esto dejará veinte habitaciones vacías y listas para los veinte nuevos huéspedes.

¿Pero qué pasa si llegan infinitos huéspedes nuevos a bordo de un autobús infinito? Podemos modificar el argumento anterior de modo que siga funcionando para esta situación: espaciar los huéspedes que ya están en el hotel de modo que sólo ocupen una de cada dos habitaciones. Matemáticamente hablando, hay que trasladar al huésped de la habitación n a la 2n, de modo que todas las habitaciones pares estén ocupadas. Esto deja todas las demás habitaciones (¡infinitamente numerosas!) vacías y listas para alojar a las (¡infinitamente numerosas!) personas que lleguen en el autobús. La persona sentada en el asiento número n del autobús debe trasladarse a la nª habitación impar, que es la habitación número 2n – 1.

¿Y si llegan noventa y nueve autobuses infinitos? Basta con trasladar a los huéspedes originales del hotel a las habitaciones 100, 200, 300, etc., a los pasajeros del primer autobús a las habitaciones 1, 101, 201, etc., a los pasajeros del segundo autobús a las habitaciones 2, 102, 202, etc., y así sucesivamente para el resto de los autobuses. Así se ocuparán todas las habitaciones del hotel sin dejar a ningún huésped sin habitación. Si los pasajeros de los autobuses estuvieran numerados 1, 2, 3, 4, 5, … (y no hagamos distinción y llamemos también pasajeros a los huéspedes originales del hotel -podemos pensar que se trata de trasladar a todos los huéspedes originales fuera del hotel y a un autobús decorativo aparcado justo fuera del hotel, al que podemos llamar autobús número 0), entonces veríamos que las primeras cien habitaciones del hotel se llenan con los pasajeros número 1, las segundas cien habitaciones del hotel se llenan con los pasajeros número 2, y así sucesivamente.

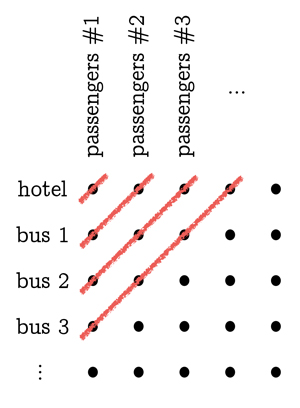
El siguiente nivel es tratar con infinitos autobuses infinitos (cada autobús con infinitos pasajeros). Lo primero que hay que hacer es sacar a todo el mundo del hotel y de los autobuses y organizarlo en forma de cuadrícula en el aparcamiento, o en un papel: haz que los huéspedes originales del hotel (es decir, los pasajeros del autobús 0) se alineen en orden, de izquierda a derecha, formando una fila. Haz que los pasajeros del primer autobús formen otra fila justo debajo, y los del segundo autobús una fila debajo de ésta, etc. Haz que las filas se alineen entre sí de manera que los pasajeros número 1 de cada autobús se alineen en una columna, los pasajeros número 2 se alineen en una columna a la derecha de ésta, y así sucesivamente. Ahora bien, si empezamos a llenar las habitaciones del hotel 1, 2, 3, 4, . . . con gente de la primera fila, nunca la terminaremos y pasaremos a la segunda fila, y lo mismo si intentamos empezar por la primera columna. El truco consiste en pensar en líneas diagonales que van de abajo a arriba en la cuadrícula. La más a la izquierda de estas líneas diagonales sólo alcanza a la persona de arriba a la izquierda (autobús 0, pasajero 1): pon a esa persona en la habitación 1. La siguiente línea diagonal alcanza a dos personas (autobús 1, pasajero 1 y autobús 0, pasajero 2): pon a esas dos personas en las habitaciones 2 y 3. La siguiente línea diagonal alcanza a tres personas: colócalas en las siguientes tres habitaciones vacías, la 4, la 5 y la 6. Siguiendo este patrón, acabaremos asignando una habitación a cada una de las personas que están pacientemente paradas en el aparcamiento.

¿Podemos profundizar en el infinito, más allá de infinitos autobuses infinitos? Sí podemos: imaginemos que justo al lado del hotel de Hilbert hay un aparcamiento. En la primera planta, justo al lado de la puerta del hotel, están nuestros ya conocidos infinitos autobuses infinitos. Pero entonces nos damos cuenta: el garaje tiene infinitas plantas, cada una con infinitos autobuses infinitos. ¿Puede el hotel Hilbert hacer frente a esta capa añadida de infinidad? La respuesta es sí. Puedes imaginar que utilizas el método anterior para hacer una sola fila de pasajeros en cada planta del aparcamiento, y luego decirle a cada fila que entre en un autobús infinito. Ahora hemos reducido el problema de nuevo a infinitos autobuses infinitos, que sabemos que se pueden acomodar en el hotel.

¿Y si añadimos otra capa de infinito? Por ejemplo, ¿si hay infinitos aparcamientos, cada uno con infinitas plantas, cada planta con infinitos autobuses, cada autobús con infinitos pasajeros? Son cuatro capas de infinito, ¡y la respuesta sigue siendo sí! De hecho, la respuesta es sí incluso para cuatro mil capas de infinito. ¿Se detiene alguna vez? ¿El hotel de Hilbert nunca deja de acoger a nuevos huéspedes? ¿Hay algún infinito que sea demasiado grande para el hotel de Hilbert?

Sí, lo hay. De hecho, si tuviéramos infinitas capas de infinito, todas esas personas no podrían alojarse en el hotel de Hilbert. Entonces… ¿qué ocurre? Resulta que todos los infinitos descritos, hasta este último, tienen el mismo tamaño. Ese tamaño se llama ℵ0 (aleph nought), el tamaño del conjunto ℕ = {1, 2, 3, 4, …} y cuántas habitaciones hay en el hotel de Hilbert. Fue Georg Cantor quien en 1874 introdujo la idea de cómo comparar los tamaños de los infinitos, y demostró que existen infinitos de diferentes tamaños. Varios matemáticos importantes (Poincaré, Kronecker y, más tarde, Weyl) se opusieron firmemente a sus ideas, al igual que algunos teólogos, que afirmaban que las ideas de Cantor ponían en tela de juicio la unicidad de la infinidad absoluta de Dios. Hilbert, en cambio, apoyó y defendió a Cantor.

Comparar tamaños de conjuntos infinitos no es tan diferente de comparar tamaños de conjuntos finitos: para saber si hay más sillas o más personas en una sala de conferencias, no hay que contar personas y sillas y comparar los dos números. Basta con echar un vistazo a la sala y ver si hay sillas vacías (más sillas que personas) o gente de pie (más personas que sillas): si todas las personas están sentadas en una silla y no hay sillas vacías, entonces el conjunto de las sillas y el conjunto de las personas tienen el mismo tamaño. Del mismo modo, si a cada pasajero de los autobuses se le asigna una habitación en el hotel de Hilbert y no queda ninguna vacía, entonces el conjunto de pasajeros es un infinito del mismo tamaño que el conjunto de habitaciones del hotel de Hilbert, ℵ0. Cantor utilizó esta idea para demostrar que el conjunto de los números reales, ℝ, es estrictamente mayor que el conjunto de los números naturales, ℕ; su hermoso argumento se conoció como «la diagonal de Cantor». Cantor también conjeturó -y trató de demostrar, pero no lo consiguió- la Hipótesis del Continuo: que no existe un conjunto infinito estrictamente mayor que ℕ pero estrictamente menor que ℝ. Hilbert incluyó la demostración de que esa afirmación es verdadera o falsa como el primer problema de la famosa lista de veintitrés problemas que presentó en el Congreso Internacional de Matemáticos de 1900 en París, que marcaría la dirección de la investigación matemática durante décadas. La respuesta es que no se puede demostrar que esta hipótesis sea falsa (Gödel, década de 1940), pero tampoco se puede demostrar que sea verdadera (Cohen, década de 1960): ¡es un problema indecidible!

Hilbert dijo célebremente, acerca de las ideas de Cantor sobre el infinito y toda la nueva matemática que aportaron: «Nadie nos expulsará del paraíso que Cantor ha creado»

.