Zu Beginn des zwanzigsten Jahrhunderts war die Universität Göttingen eine der führenden Forschungsstätten für Mathematik in der Welt. Der Mathematiker David Hilbert war dort ein etablierter Professor, und im Wintersemester 1924-25 hielt er eine Reihe von Vorlesungen über das Unendliche in Mathematik, Physik und Astronomie. (Diese und andere Vorlesungen von Hilbert sind jetzt in Buchform im Springer-Verlag erschienen. Das Buch ist in der IAS-Bibliothek in Übersetzung und im deutschen Original erhältlich). In einer dieser Vorlesungen erläuterte er anhand eines Beispiels den entscheidenden Unterschied zwischen endlichen und unendlichen Mengen: Wenn in einem Hotel mit einer endlichen Anzahl von Zimmern alle Zimmer belegt sind, gibt es keinen Platz für neue Gäste. In einem Hotel mit unendlich vielen Zimmern ist dies jedoch kein Problem: Wenn alle Zimmer belegt sind und ein neuer Gast eintrifft, wird einfach jedes alte Zimmer um ein weiteres Zimmer verschoben, so dass das erste Zimmer für den neu eingetroffenen Gast frei bleibt. Mit einem ähnlichen Argument können wir jede endliche Anzahl und sogar unendlich viele neu ankommende Gäste unterbringen.

George Gamow (der Verfasser des berühmten Alpher-Bethe-Gamow-Papiers auf dem Gebiet der physikalischen Kosmologie) war ein paar Jahre nach diesen Vorlesungen als Postdoc an der Universität Göttingen tätig und hat dort wahrscheinlich von Hilberts Beispiel des unendlichen Hotels erfahren. Er popularisierte es 1947 in seinem populärwissenschaftlichen Buch mit dem Titel One Two Three…Infinity: Fakten und Spekulationen der Wissenschaft (erhältlich in der Bibliothek der Princeton University).

Lassen Sie uns zu Hilberts Hotel zurückkehren. Der Einfachheit halber nehmen wir an, dass die unendlich vielen Zimmer des Hotels mit 1, 2, 3, 4, 5, … nummeriert sind. Eines Abends sind sie alle belegt, aber ein neuer Gast kommt an. Wie schon gesagt, verlegen wir einfach den Gast in Zimmer 1 in Zimmer 2, den in Zimmer 2 in Zimmer 3, den in Zimmer 3 in Zimmer 4 und ganz allgemein den Gast in Zimmer n in Zimmer n + 1, wodurch in Zimmer 1 ein Platz für den neuen Gast frei wird, aber keiner der ursprünglichen Gäste obdachlos wird.

Sagen wir nun, es kommen zwanzig neue Gäste an, statt nur einem. Der zuvor angewandte Trick funktioniert genauso gut: Der Gast in Zimmer 1 wird in Zimmer 21 untergebracht, der Gast in Zimmer 2 in Zimmer 22 und generell der Gast in Zimmer n in Zimmer n + 20. Auf diese Weise bleiben zwanzig Zimmer frei und sind bereit für zwanzig neue Gäste.

Was aber, wenn unendlich viele neue Gäste an Bord eines unendlichen Busses ankommen? Wir können das vorherige Argument so abändern, dass es auch in diesem Fall funktioniert: Wir verteilen die bereits im Hotel befindlichen Gäste so, dass sie nur jedes zweite Zimmer belegen. Mathematisch ausgedrückt: Verlegen Sie den Gast in Zimmer n in Zimmer 2n, so dass alle geradzahligen Zimmer belegt sind. Damit bleibt jedes andere Zimmer (unendlich viele!) frei und bereit, die (unendlich vielen!) Personen aufzunehmen, die mit dem Bus ankommen. Die Person, die im Bus auf dem Platz Nummer n sitzt, sollte in das n-te ungerade nummerierte Zimmer ziehen, also in das Zimmer Nummer 2n – 1.

Was ist, wenn neunundneunzig unendliche Busse ankommen? Man bringt die ursprünglichen Hotelgäste in die Zimmer 100, 200, 300 usw., die Passagiere des ersten Busses in die Zimmer 1, 101, 201 usw., die Passagiere des zweiten Busses in die Zimmer 2, 102, 202 usw., und so weiter für die restlichen Busse. Auf diese Weise werden alle Zimmer des Hotels belegt, ohne dass ein Gast ohne Zimmer bleibt. Wenn die Fahrgäste in den Bussen selbst mit den Nummern 1, 2, 3, 4, 5, … (und lassen Sie uns keinen Unterschied machen und die ursprünglichen Gäste des Hotels ebenfalls als Passagiere bezeichnen – wir können uns das so vorstellen, dass alle ursprünglichen Gäste aus dem Hotel in einen dekorativen Bus gebracht werden, der direkt vor dem Hotel geparkt ist und den wir Bus Nummer 0 nennen können), dann würden wir sehen, dass die ersten hundert Zimmer des Hotels mit Passagieren Nummer 1 gefüllt sind, die zweiten hundert Zimmer des Hotels mit Passagieren Nummer 2 und so weiter.

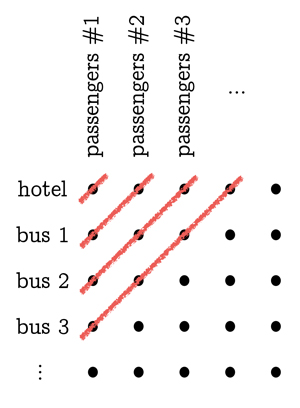
Die nächste Stufe ist der Umgang mit unendlich vielen unendlichen Bussen (jeder Bus mit unendlich vielen Passagieren). Als Erstes müssen alle aus dem Hotel und aus den Bussen herausgeholt und auf dem Parkplatz oder auf einem Blatt Papier gitterförmig angeordnet werden: Die ursprünglichen Gäste des Hotels (d.h. die Fahrgäste von Bus 0) sollen sich in einer Reihe von links nach rechts aufstellen und eine Reihe bilden. Die Fahrgäste des ersten Busses sollen eine weitere Reihe direkt darunter bilden, die Fahrgäste des zweiten Busses eine Reihe darunter, usw. Stellen Sie die Reihen so aneinander, dass die Fahrgäste mit der Nummer 1 jedes Busses in einer Spalte stehen, die Fahrgäste mit der Nummer 2 in einer Spalte rechts von dieser und so weiter. Wenn wir nun damit beginnen, die Hotelzimmer 1, 2, 3, 4, … mit Leuten aus der ersten Reihe zu füllen, werden wir nie fertig und müssen mit der zweiten Reihe weitermachen, und das Gleiche gilt, wenn wir mit der ersten Spalte beginnen. Der Trick besteht darin, sich diagonale Linien vorzustellen, die auf dem Raster von unten links nach oben rechts verlaufen. Die äußerste linke dieser diagonalen Linien trifft nur die eine Person oben links (Bus 0, Fahrgast 1): Setzen Sie diese Person in Raum 1. Die nächste diagonale Linie trifft zwei Personen (Bus 1, Fahrgast 1 und Bus 0, Fahrgast 2): Setzen Sie diese beiden Personen in die Räume 2 und 3. Die nächste diagonale Linie trifft drei Personen: Stecken Sie sie in die nächsten drei leeren Räume 4, 5, 6. Wenn wir dieses Muster fortsetzen, werden wir schließlich jeder der geduldig auf dem Parkplatz stehenden Personen ein Zimmer zuweisen.

Können wir noch tiefer in die Unendlichkeit gehen, tiefer als unendlich viele unendliche Busse? Ja, das können wir: Stellen Sie sich vor, dass sich direkt neben Hilberts Hotel ein Parkhaus befindet. Im ersten Stock, direkt neben der Hoteltür, stehen unsere bereits bekannten unendlich vielen unendlichen Busse. Doch dann stellen wir fest: Das Parkhaus hat unendlich viele Stockwerke, auf denen jeweils unendlich viele unendliche Busse stehen. Kann das Hilbert-Hotel mit dieser zusätzlichen Ebene der Unendlichkeit umgehen? Die Antwort lautet: Ja! Man kann sich vorstellen, dass man mit der vorherigen Methode auf jeder Etage des Parkhauses eine einzelne Reihe von Fahrgästen bildet und dann jeder einzelnen Reihe sagt, dass sie in einen unendlichen Bus einsteigen soll. Jetzt haben wir das Problem auf unendlich viele unendliche Busse reduziert, von denen wir wissen, dass sie im Hotel untergebracht werden können.

Was, wenn wir eine weitere Ebene der Unendlichkeit hinzufügen? Zum Beispiel, wenn es unendlich viele Parkhäuser gibt, jedes mit unendlich vielen Stockwerken, jedes Stockwerk mit unendlich vielen Bussen, jeder Bus mit unendlich vielen Fahrgästen? Das sind vier Schichten der Unendlichkeit, und die Antwort ist immer noch ja! Tatsächlich ist die Antwort sogar für viertausend Schichten der Unendlichkeit ja. Hört das jemals auf? Kann Hilberts Hotel jemals keine neuen Gäste mehr aufnehmen? Gibt es eine Unendlichkeit, die zu groß für Hilberts Hotel ist?

Ja, die gibt es. Wenn wir nämlich unendlich viele Schichten der Unendlichkeit hätten, könnten all diese Menschen unmöglich in Hilberts Hotel untergebracht werden. Also … was passiert hier? Es stellt sich heraus, dass alle beschriebenen Unendlichkeiten, bis auf diese letzte, die gleiche Größe haben. Diese Größe wird ℵ0 (aleph nought) genannt, die Größe der Menge ℕ = {1, 2, 3, 4, …} und wie viele Zimmer es in Hilberts Hotel gibt. Es war Georg Cantor, der 1874 die Idee vorstellte, wie man die Größe von Unendlichkeiten vergleichen kann, und zeigte, dass es Unendlichkeiten unterschiedlicher Größe gibt. Mehrere bedeutende Mathematiker (Poincaré, Kronecker und später Weyl) widersprachen seinen Ideen heftig, ebenso wie einige Theologen, die behaupteten, Cantors Ideen würden die Einzigartigkeit der absoluten Unendlichkeit Gottes in Frage stellen. Hilbert hingegen unterstützte und verteidigte Cantor.

Der Vergleich der Größe unendlicher Mengen unterscheidet sich nicht so sehr von dem Vergleich der Größe endlicher Mengen: Um zu wissen, ob es mehr Stühle oder mehr Personen in einem Hörsaal gibt, muss man nicht die Personen und Stühle zählen und die beiden Zahlen vergleichen. Man kann einfach einen Blick in den Raum werfen und sehen, ob es leere Stühle (mehr Stühle als Personen) oder stehende Personen (mehr Personen als Stühle) gibt: Wenn jede einzelne Person auf einem Stuhl sitzt und es keine leeren Stühle gibt, dann sind die Menge der Stühle und die Menge der Personen gleich groß. Ähnlich verhält es sich, wenn jeder Fahrgast in den Bussen ein Zimmer in Hilberts Hotel zugewiesen bekommt und kein Zimmer leer bleibt, dann ist die Menge der Fahrgäste eine Unendlichkeit von derselben Größe wie die Menge der Zimmer in Hilberts Hotel, ℵ0. Cantor nutzte diese Idee, um zu zeigen, dass die Menge der reellen Zahlen, ℝ, streng größer ist als die Menge der natürlichen Zahlen, ℕ; sein schönes Argument wurde als „Cantors Diagonale“ bekannt. Cantor vermutete auch die Kontinuumshypothese, die er zu beweisen versuchte, aber scheiterte: dass es keine unendliche Menge gibt, die streng größer als ℕ, aber streng kleiner als ℝ ist. Hilbert stellte den Beweis, ob diese Aussage wahr oder falsch ist, als erstes Problem auf die berühmte Liste von dreiundzwanzig Problemen, die er 1900 auf dem Internationalen Mathematikerkongress in Paris vorstellte und die die Richtung der mathematischen Forschung für die nächsten Jahrzehnte bestimmen sollte. Die Antwort ist, dass diese Hypothese nicht als falsch bewiesen werden kann (Gödel, 1940er Jahre), aber sie kann auch nicht als wahr bewiesen werden (Cohen, 1960er Jahre): es ist ein unentscheidbares Problem!

Hilbert sagte berühmt über Cantors Ideen über die Unendlichkeit und all die neue Mathematik, die sie hervorgebracht haben: „Niemand wird uns aus dem Paradies vertreiben, das Cantor geschaffen hat.“