All’inizio del ventesimo secolo, l’Università di Gottinga era uno dei migliori centri di ricerca di matematica del mondo. Il matematico David Hilbert era un professore affermato e durante il semestre invernale del 1924-25 tenne una serie di conferenze sull’infinito in matematica, fisica e astronomia. (Queste e altre conferenze di Hilbert sono ora pubblicate in forma di libro da Springer-Verlag. Il libro è disponibile presso la biblioteca IAS in traduzione e nell’originale tedesco). In una di queste lezioni, ha usato un esempio per spiegare la differenza cruciale tra insiemi finiti e infiniti: in un hotel con un numero finito di stanze, se tutte le stanze sono occupate allora non c’è spazio per nuovi ospiti. Ma in un hotel con un numero infinito di stanze questo non è un problema: se tutte le stanze sono occupate e arriva un nuovo ospite, basta spostare ogni vecchio ospite di una stanza, lasciando la prima stanza libera per il nuovo ospite. Un argomento simile ci permette di ospitare qualsiasi numero finito, e anche infinito, di nuovi ospiti.

George Gamow (autore del famoso documento Alpher-Bethe-Gamow nel campo della cosmologia fisica) era un postdoc estivo all’Università di Göttingen pochi anni dopo queste conferenze e probabilmente ha imparato lì l’esempio di Hilbert dell’hotel infinito. Lo rese popolare nel suo libro di divulgazione scientifica del 1947 intitolato One Two Three…Infinity: Facts and Speculations of Science (disponibile presso la biblioteca dell’Università di Princeton).

Torniamo all’hotel di Hilbert. Per rendere le cose più chiare, diciamo che le infinite stanze dell’hotel sono numerate 1, 2, 3, 4, 5, . . . Una notte sono tutte occupate ma arriva un nuovo ospite. Come abbiamo detto prima, spostiamo semplicemente l’ospite della stanza 1 nella stanza 2, quello della stanza 2 nella stanza 3, quello della stanza 3 nella stanza 4 e, in generale, l’ospite della stanza n nella stanza n + 1, creando così un posto libero nella stanza 1 per il nuovo ospite, ma non lasciando nessuno degli ospiti originali senza casa.

Ora diciamo che arrivano venti nuovi ospiti invece di uno solo. Il trucco usato prima funziona altrettanto bene: spostate l’ospite della stanza 1 nella stanza 21, l’ospite della stanza 2 nella stanza 22 e, in generale, l’ospite della stanza n nella stanza n + 20. Questo lascerà venti stanze libere e pronte per i venti nuovi ospiti.

Ma cosa succede se infiniti nuovi ospiti arrivano a bordo di un autobus infinito? Possiamo modificare il ragionamento precedente in modo che funzioni ancora per questa situazione: distanziare gli ospiti già presenti nell’hotel in modo che occupino solo ogni altra stanza. Matematicamente parlando, spostiamo l’ospite della stanza n nella stanza 2n, in modo che tutte le stanze pari siano occupate. Questo lascia tutte le altre stanze (infinitamente tante!) libere e pronte ad accogliere le persone (infinitamente tante!) che arrivano con l’autobus. La persona seduta nel posto numero n sull’autobus dovrebbe spostarsi nell’ennesima stanza dispari, che è la stanza numero 2n – 1.

E se arrivano novantanove autobus infiniti? Basta spostare gli ospiti originali dell’hotel nelle camere 100, 200, 300, ecc., i passeggeri del primo autobus nelle camere 1, 101, 201, ecc., i passeggeri del secondo autobus nelle camere 2, 102, 202, ecc. e così via per gli altri autobus. Ciò occuperà tutte le stanze dell’hotel senza lasciare nessun ospite senza stanza. Se i passeggeri degli autobus fossero essi stessi numerati 1, 2, 3, 4, 5, . . . (e non facciamo distinzioni e chiamiamo passeggeri anche gli ospiti originali dell’hotel: possiamo pensare a questo come a spostare tutti gli ospiti originali fuori dall’hotel e in un autobus decorativo parcheggiato proprio fuori dall’hotel, che possiamo chiamare autobus numero 0), allora vedremmo le prime cento stanze dell’hotel riempirsi di passeggeri numero 1, le seconde cento stanze dell’hotel riempirsi di passeggeri numero 2, e così via.

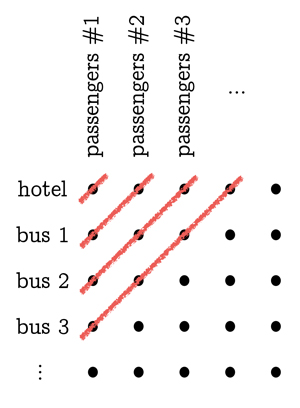
Il livello successivo è trattare con infiniti autobus infiniti (ogni autobus con infiniti passeggeri). La prima cosa da fare è far uscire tutti dall’hotel e dagli autobus e organizzarli in forma di griglia nel parcheggio, o su un pezzo di carta: fai allineare gli ospiti originali dell’hotel (cioè i passeggeri dell’autobus 0) in ordine, da sinistra a destra, formando una fila. Fai in modo che i passeggeri del primo autobus formino un’altra fila appena sotto, e i passeggeri del secondo autobus una fila sotto quella, ecc. Fate in modo che le file si allineino tra loro in modo che i passeggeri numero 1 di ogni autobus si allineino in una colonna, i passeggeri numero 2 si allineino in una colonna a destra di quella, e così via. Ora, se iniziamo a riempire le camere d’albergo 1, 2, 3, 4, . . . con persone della prima fila, non la finiremo mai e passeremo alla seconda fila, e allo stesso modo se cerchiamo di iniziare con la prima colonna. Il trucco è pensare a linee diagonali che corrono dal basso a sinistra all’alto a destra sulla griglia. La più a sinistra di queste linee diagonali colpisce solo una persona in alto a sinistra (bus 0, passeggero 1): metti quella persona nella stanza 1. La linea diagonale successiva colpisce due persone (bus 1, passeggero 1 e bus 0, passeggero 2): metti quelle due persone nelle stanze 2 e 3. La prossima linea diagonale colpisce tre persone: mettile nelle prossime tre stanze vuote, 4, 5, 6. Continuando questo schema alla fine assegneremo una stanza a ciascuna delle persone che stanno pazientemente in piedi nel parcheggio.

Possiamo andare più a fondo nell’infinito, più a fondo di infiniti autobus infiniti? Sì, possiamo: immaginate che proprio accanto all’hotel di Hilbert ci sia un parcheggio. Al primo piano, proprio accanto alla porta dell’hotel, ci sono i nostri già noti infiniti autobus infiniti. Ma poi notiamo: il garage ha infiniti piani, ognuno con infiniti infiniti autobus. Può l’hotel Hilbert gestire questo strato di infinito aggiunto? La risposta è sì! Si può immaginare di usare il metodo precedente per fare una singola fila di passeggeri su ogni piano del garage, e poi dire ad ogni singola fila di andare in un autobus infinito. Ora abbiamo ridotto il problema a un numero infinito di autobus infiniti, che sappiamo poter ospitare nell’hotel.

E se aggiungessimo un altro livello di infinito? Per esempio, se ci sono infiniti parcheggi, ognuno con infiniti piani, ogni piano con infiniti autobus, ogni autobus con infiniti passeggeri? Sono quattro strati di infinito, e la risposta è ancora sì! In effetti, la risposta è sì anche per quattromila strati di infinito. Si ferma mai? L’hotel di Hilbert non riesce mai ad accogliere nuovi ospiti? Esiste un infinito troppo grande per l’hotel di Hilbert?

Sì, esiste. Infatti, se avessimo infiniti strati di infinito, tutte quelle persone non potrebbero essere ospitate nell’hotel di Hilbert. Quindi… cosa sta succedendo? Si scopre che tutti gli infiniti descritti, fino a quest’ultimo, hanno la stessa dimensione. Questa dimensione si chiama ℵ0 (aleph nought), la dimensione dell’insieme ℕ = {1, 2, 3, 4, . . .} e quante stanze ci sono nell’hotel di Hilbert. Fu Georg Cantor che nel 1874 introdusse l’idea di come confrontare le dimensioni degli infiniti, e mostrò che esistono infiniti di dimensioni diverse. Diversi matematici importanti (Poincaré, Kronecker, e più tardi Weyl) si opposero fortemente alle sue idee, così come alcuni teologi – questi sostenevano che le idee di Cantor sfidavano l’unicità dell’infinito assoluto di Dio. Hilbert, d’altra parte, sostenne e difese Cantor.

Confrontare le dimensioni di insiemi infiniti non è così diverso dal confrontare le dimensioni di insiemi finiti: per sapere se ci sono più sedie o più persone in una sala conferenze, non è necessario contare le persone e le sedie e confrontare i due numeri. Si può semplicemente dare un’occhiata alla stanza e vedere se ci sono sedie vuote (più sedie che persone) o persone rimaste in piedi (più persone che sedie): se ogni singola persona è seduta su una sedia e non ci sono sedie vuote, allora l’insieme delle sedie e l’insieme delle persone sono della stessa dimensione. Allo stesso modo, se ad ogni passeggero degli autobus viene assegnata una stanza nell’hotel di Hilbert e nessuna stanza rimane vuota, allora l’insieme dei passeggeri è un infinito della stessa dimensione dell’insieme delle stanze dell’hotel di Hilbert, ℵ0. Cantor usò questa idea per dimostrare che l’insieme dei numeri reali, ℝ, è strettamente più grande dell’insieme dei numeri naturali, ℕ; il suo bellissimo argomento divenne noto come “diagonale di Cantor”. Cantor ha anche congetturato e cercato di dimostrare, ma senza successo, l’Ipotesi del Continuo: che non esiste un insieme infinito strettamente più grande di ℕ ma strettamente più piccolo di ℝ. Hilbert incluse la dimostrazione che questa affermazione è vera o falsa come primo problema nella famosa lista di ventitré problemi che presentò al Congresso Internazionale dei Matematici di Parigi del 1900, che avrebbe plasmato la direzione della ricerca matematica per i decenni a venire. La risposta è che questa ipotesi non può essere dimostrata come falsa (Gödel, anni ’40) ma non può nemmeno essere dimostrata come vera (Cohen, anni ’60): è un problema indecidibile!

Hilbert disse notoriamente, a proposito delle idee di Cantor sull’infinito e di tutta la nuova matematica che esse portarono: “Nessuno ci espellerà dal paradiso che Cantor ha creato”

.