Ospitalitate la hotelul Hilbert
La începutul secolului al XX-lea, Universitatea din Göttingen era unul dintre cele mai importante centre de cercetare în domeniul matematicii din lume. Matematicianul David Hilbert era un profesor bine stabilit acolo, iar în timpul semestrului de iarnă din 1924-25 a ținut o serie de prelegeri despre infinitul în matematică, fizică și astronomie. (Aceste prelegeri și alte prelegeri ale lui Hilbert sunt publicate în prezent sub formă de carte de către Springer-Verlag. Cartea este disponibilă la biblioteca IAS în traducere și în originalul german). Într-una dintre aceste prelegeri, el a folosit un exemplu pentru a explica diferența crucială dintre seturile finite și infinite: într-un hotel cu un număr finit de camere, dacă toate camerele sunt ocupate, atunci nu există loc pentru noi oaspeți. Dar într-un hotel cu un număr infinit de camere, acest lucru nu reprezintă o problemă: dacă toate camerele sunt ocupate și sosește un nou oaspete, pur și simplu se mută fiecare oaspete vechi cu o cameră mai încolo, lăsând prima cameră liberă pentru oaspetele nou sosit. Un argument similar ne permite să găzduim orice număr finit și chiar infinit de mulți oaspeți nou sosiți.
George Gamow (autorul celebrei lucrări Alpher-Bethe-Gamow în domeniul cosmologiei fizice) a fost postdoctorand de vară la Universitatea din Göttingen la câțiva ani după ce au avut loc aceste prelegeri și, probabil, a aflat de exemplul lui Hilbert al hotelului infinit acolo. El l-a popularizat în cartea sa de popularizare a științei din 1947, intitulată One Two Three…Infinity: Facts and Speculations of Science (disponibilă la biblioteca Universității Princeton).
Să ne întoarcem la hotelul lui Hilbert. Pentru a face lucrurile mai ordonate, să spunem că infinit de multe camere ale hotelului sunt numerotate cu 1, 2, 3, 3, 4, 5, … … . Într-o noapte, toate sunt ocupate, dar sosește un nou oaspete. Așa cum am spus mai devreme, pur și simplu mutăm oaspetele din camera 1 în camera 2, cel din camera 2 în camera 3, cel din camera 3 în camera 4 și, în general, oaspetele din camera n în camera n + 1, creând astfel un loc liber în camera 1 pentru noul oaspete, dar fără ca niciunul dintre oaspeții inițiali să rămână fără adăpost.
Să spunem acum că sosesc douăzeci de oaspeți noi în loc de unul singur. Trucul folosit anterior funcționează la fel de bine: mutați oaspetele din camera 1 în camera 21, oaspetele din camera 2 în camera 22 și, în general, oaspetele din camera n în camera n + 20. Acest lucru va lăsa douăzeci de camere libere și pregătite pentru cei douăzeci de oaspeți noi.
Dar ce se întâmplă dacă la bordul unui autobuz infinit sosesc infinit de mulți oaspeți noi? Putem modifica argumentul anterior astfel încât să funcționeze în continuare pentru această situație: spațiați oaspeții care se află deja în hotel astfel încât să ocupe doar o cameră din două. Matematic vorbind, mutați oaspetele din camera n în camera 2n, astfel încât toate camerele cu numere pare să fie ocupate. Astfel, toate celelalte camere (infinit de multe!) rămân libere și pregătite să găzduiască (infinit de multe!) persoanele care sosesc cu autobuzul. Persoana care stă pe locul cu numărul n din autobuz ar trebui să se mute în a n-a cameră cu număr impar, care este camera cu numărul 2n – 1.
Ce se întâmplă dacă sosesc nouăzeci și nouă de autobuze infinite? Pur și simplu mutați oaspeții hotelului inițial în camerele 100, 200, 300 etc., pasagerii din primul autobuz în camerele 1, 101, 201 etc., pasagerii din al doilea autobuz în camerele 2, 102, 202 etc. și așa mai departe pentru restul autobuzelor. Astfel, toate camerele hotelului vor fi ocupate, fără ca vreun client să rămână fără cameră. În cazul în care pasagerii din autobuze ar fi numerotați cu 1, 2, 3, 4, 5, . . . (și să nu facem nicio distincție și să-i numim pasageri și pe oaspeții inițiali ai hotelului – ne putem gândi la aceasta ca și cum i-am muta pe toți oaspeții inițiali din hotel într-un autobuz decorativ parcat chiar în fața hotelului, pe care îl putem numi autobuzul cu numărul 0), atunci vom vedea că primele o sută de camere ale hotelului sunt ocupate de pasagerii cu numărul 1, a doua sută de camere ale hotelului sunt ocupate de pasagerii cu numărul 2, și așa mai departe.
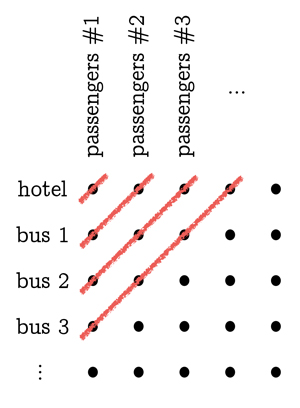
Nivelul următor se ocupă de un număr infinit de autobuze infinite (fiecare autobuz cu un număr infinit de pasageri). Primul lucru care trebuie făcut este să îi scoatem pe toți din hotel și din autobuze și să îi organizăm în formă de grilă în parcare sau pe o bucată de hârtie: puneți-i pe oaspeții inițiali ai hotelului (a.k.a., pasagerii autobuzului 0) să se alinieze în ordine, de la stânga la dreapta, formând un rând. Puneți-i pe pasagerii de la primul autobuz să formeze un alt rând chiar sub acesta, iar pe pasagerii de la al doilea autobuz un rând sub acesta, etc. Faceți ca rândurile să se alinieze între ele, astfel încât pasagerii cu numărul 1 din fiecare autobuz să se alinieze într-o coloană, pasagerii cu numărul 2 să se alinieze într-o coloană la dreapta acesteia și așa mai departe. Acum, dacă începem să umplem camerele de hotel 1, 2, 3, 4, . . . . cu persoane din primul rând, nu le vom termina niciodată și vom trece la al doilea rând, și la fel dacă încercăm să începem cu prima coloană. Trucul este să ne gândim la linii diagonale, care merg de jos în stânga până sus în dreapta pe grilă. Cea mai din stânga dintre aceste linii diagonale atinge doar o singură persoană din stânga sus (autobuzul 0, pasagerul 1): puneți acea persoană în camera 1. Următoarea linie diagonală atinge două persoane (autobuzul 1, pasagerul 1 și autobuzul 0, pasagerul 2): puneți aceste două persoane în camerele 2 și 3. Următoarea linie diagonală atinge trei persoane: așezați-le în următoarele trei camere goale, 4, 5, 6. Continuând acest tipar, în cele din urmă vom atribui câte o cameră fiecăruia dintre oamenii care stau răbdători în parcare.
Pot fi mai adânc în infinit, mai adânc decât infinit de multe autobuze infinite? Da, putem: imaginați-vă că chiar lângă hotelul lui Hilbert se află o parcare. La primul etaj, chiar lângă ușa hotelului, se află autobuzele noastre deja cunoscute, infinit de multe autobuze infinite. Dar apoi observăm: garajul are un număr infinit de etaje, fiecare cu un număr infinit de autobuze infinite. Poate hotelul Hilbert să se descurce cu acest strat suplimentar de infinitate? Răspunsul este da! Vă puteți imagina că puteți folosi metoda anterioară pentru a face un singur rând de pasageri la fiecare etaj al parcării, apoi spuneți-i fiecărui rând să urce într-un autobuz infinit. Acum am redus problema înapoi la un număr infinit de autobuze infinite, despre care știm că pot fi găzduite în hotel.
Ce se întâmplă dacă adăugăm un alt strat de infinit? De exemplu, dacă există infinit de multe parcări, fiecare cu infinit de multe etaje, fiecare etaj cu infinit de multe autobuze, fiecare autobuz cu infinit de mulți pasageri? Asta înseamnă patru straturi de infinit, iar răspunsul este tot da! De fapt, răspunsul este da chiar și pentru patru mii de straturi de infinit. Se oprește vreodată? Oare hotelul lui Hilbert nu reușește vreodată să găzduiască noi oaspeți? Există un infinit care să fie prea mare pentru hotelul lui Hilbert?
Da, există. Într-adevăr, dacă am avea infinit de multe straturi de infinit, toți acești oameni nu ar putea fi cazați în hotelul lui Hilbert. Deci …ce se întâmplă? Se pare că toate infiniturile descrise, până la acesta din urmă, sunt de aceeași mărime. Această dimensiune se numește ℵ0 (aleph zero), dimensiunea setului ℕ = {1, 2, 3, 3, 4, . . .} și câte camere există la hotelul lui Hilbert. Georg Cantor a fost cel care, în 1874, a introdus ideea de a compara dimensiunile infinitelor și a arătat că există infinite de dimensiuni diferite. Mai mulți matematicieni importanți (Poincaré, Kronecker și, mai târziu, Weyl) s-au opus cu vehemență ideilor sale, la fel ca și unii teologi – aceștia au susținut că ideile lui Cantor contestau unicitatea infinitului absolut al lui Dumnezeu. Hilbert, pe de altă parte, l-a susținut și apărat pe Cantor.
Compararea mărimilor unor seturi infinite nu este atât de diferită de compararea mărimilor unor seturi finite: pentru a ști dacă sunt mai multe scaune sau mai multe persoane într-o sală de lectură, nu trebuie să numărați persoanele și scaunele și să comparați cele două numere. Puteți doar să aruncați o privire în sală și să vedeți dacă există scaune goale (mai multe scaune decât persoane) sau persoane rămase în picioare (mai multe persoane decât scaune): dacă fiecare persoană este așezată pe un scaun și nu există scaune goale, atunci setul de scaune și setul de persoane au aceeași dimensiune. În mod similar, dacă fiecărui pasager din autobuze i se atribuie o cameră în hotelul lui Hilbert și nu rămâne nicio cameră goală, atunci setul de pasageri este un infinit de aceeași mărime ca și setul de camere din hotelul lui Hilbert, ℵ0. Cantor a folosit această idee pentru a demonstra că setul numerelor reale, ℝ, este strict mai mare decât setul numerelor naturale, ℕ; frumosul său argument a devenit cunoscut sub numele de „diagonala lui Cantor”. De asemenea, Cantor a conchis – și a încercat să demonstreze, dar nu a reușit – Ipoteza Continuumului: că nu există un set infinit strict mai mare decât ℕ, dar strict mai mic decât ℝ. Hilbert a inclus demonstrarea faptului că această afirmație este adevărată sau falsă drept prima problemă de pe faimoasa listă de douăzeci și trei de probleme pe care a prezentat-o la Congresul Internațional al Matematicienilor din 1900 de la Paris, care avea să modeleze direcția cercetării matematice pentru deceniile următoare. Răspunsul este că această ipoteză nu poate fi dovedită ca fiind falsă (Gödel, anii 1940), dar nici că nu poate fi dovedită ca fiind adevărată (Cohen, anii 1960): este o problemă indecidabilă!
Hilbert a spus celebru, despre ideile lui Cantor despre infinit și despre toată matematica nouă pe care acestea au adus-o. „Nu este o problemă indecidabilă: „Nimeni nu ne va alunga din paradisul pe care Cantor l-a creat.”
.