Hospitalité à l’hôtel Hilbert
Au début du vingtième siècle, l’université de Göttingen était l’un des meilleurs centres de recherche en mathématiques au monde. Le mathématicien David Hilbert y était un professeur bien établi et, pendant le semestre d’hiver 1924-25, il a donné une série de conférences sur l’infini en mathématiques, en physique et en astronomie. (Ces conférences et d’autres de Hilbert sont maintenant publiées sous forme de livre par Springer-Verlag. Le livre est disponible à la bibliothèque de l’IAS en traduction et en version originale allemande). Dans l’une de ces conférences, il a utilisé un exemple pour expliquer la différence cruciale entre les ensembles finis et infinis : dans un hôtel avec un nombre fini de chambres, si toutes les chambres sont occupées, il n’y a pas de place pour de nouveaux clients. Mais dans un hôtel avec un nombre infini de chambres, ce n’est pas un problème : si toutes les chambres sont occupées et qu’un nouveau client arrive, il suffit de déplacer chaque ancien client d’une chambre, laissant la première chambre vacante pour le nouveau client. Un argument similaire nous permet d’accueillir n’importe quel nombre fini, et même infini, d’invités nouvellement arrivés.
George Gamow (du célèbre article Alpher-Bethe-Gamow dans le domaine de la cosmologie physique) était un postdoc d’été à l’Université de Göttingen quelques années après ces conférences et a probablement appris l’exemple de l’hôtel infini de Hilbert là-bas. Il l’a popularisé dans son livre de vulgarisation scientifique de 1947 intitulé One Two Three…Infinity : Facts and Speculations of Science (disponible à la bibliothèque de l’université de Princeton).
Revenons à l’hôtel de Hilbert. Pour rendre les choses nettes, disons que les chambres de l’hôtel, infiniment nombreuses, sont numérotées 1, 2, 3, 4, 5, … . Une nuit, elles sont toutes occupées mais un nouveau client arrive. Comme nous l’avons dit précédemment, il suffit de déplacer le client de la chambre 1 vers la chambre 2, celui de la chambre 2 vers la chambre 3, celui de la chambre 3 vers la chambre 4, et en général, le client de la chambre n vers la chambre n + 1, créant ainsi une place libre dans la chambre 1 pour le nouveau client, mais ne laissant aucun des clients d’origine sans abri.
Disons maintenant que vingt nouveaux clients arrivent au lieu d’un seul. L’astuce utilisée précédemment fonctionne tout aussi bien : déplacez l’invité de la chambre 1 vers la chambre 21, l’invité de la chambre 2 vers la chambre 22, et en général, l’invité de la chambre n vers la chambre n + 20. Cela laissera vingt chambres vacantes et prêtes à accueillir les vingt nouveaux invités.
Mais que faire si une infinité de nouveaux invités arrivent à bord d’un bus infini ? Nous pouvons modifier l’argument précédent pour qu’il fonctionne toujours pour cette situation : espacer les clients déjà présents dans l’hôtel pour qu’ils n’occupent qu’une chambre sur deux. Mathématiquement parlant, déplacez le client de la chambre n vers la chambre 2n, de sorte que toutes les chambres paires soient occupées. Ainsi, toutes les autres chambres (infiniment nombreuses !) sont libres et prêtes à accueillir les personnes (infiniment nombreuses !) qui arrivent en bus. La personne assise sur le siège numéro n du bus doit s’installer dans la nième chambre impaire, qui est la chambre numéro 2n – 1.
Que faire si quatre-vingt-dix-neuf bus infinis arrivent ? Il suffit de déplacer les clients initiaux de l’hôtel dans les chambres 100, 200, 300, etc…, les passagers du premier bus dans les chambres 1, 101, 201, etc…, les passagers du deuxième bus dans les chambres 2, 102, 202, etc…, et ainsi de suite pour le reste des bus. Cela permet d’occuper toutes les chambres de l’hôtel tout en ne laissant aucun client sans chambre. Si les passagers des bus étaient eux-mêmes numérotés 1, 2, 3, 4, 5, …. (et ne faisons pas de distinction et appelons les clients d’origine de l’hôtel des passagers également – nous pouvons penser que cela revient à déplacer tous les clients d’origine hors de l’hôtel et dans un bus décoratif garé juste à l’extérieur de l’hôtel, que nous pouvons appeler le bus numéro 0), alors nous verrions les cent premières chambres de l’hôtel remplies par les passagers numéro 1, les cent secondes chambres de l’hôtel remplies par les passagers numéro 2, et ainsi de suite.
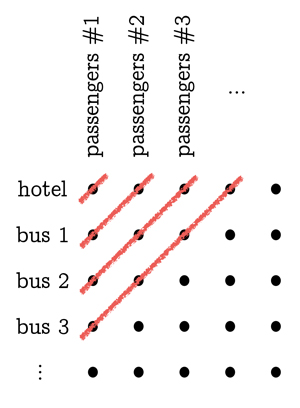
Le niveau suivant consiste à traiter une infinité de bus infinis (chaque bus ayant une infinité de passagers). La première chose à faire est de faire sortir tout le monde de l’hôtel et des bus et de les organiser sous forme de grille dans le parking, ou sur une feuille de papier : demandez aux clients d’origine de l’hôtel (alias les passagers du bus 0) de s’aligner dans l’ordre, de gauche à droite, en formant une rangée. Demandez aux passagers du premier bus de former une autre rangée juste en dessous, et aux passagers du deuxième bus une rangée en dessous de celle-là, etc. Faites en sorte que les rangées s’alignent les unes avec les autres de sorte que les passagers numéro 1 de chaque bus s’alignent dans une colonne, les passagers numéro 2 s’alignent dans une colonne à droite de celle-ci, et ainsi de suite. Maintenant, si nous commençons à remplir les chambres d’hôtel 1, 2, 3, 4, … avec les personnes de la première rangée, nous ne pourrons jamais la terminer et passerons à la deuxième rangée, et il en va de même si nous essayons de commencer par la première colonne. L’astuce consiste à penser à des lignes diagonales, allant du bas à gauche au haut à droite de la grille. La ligne diagonale la plus à gauche ne touche que la personne en haut à gauche (bus 0, passager 1) : mettez cette personne dans la pièce 1. La ligne diagonale suivante touche deux personnes (bus 1, passager 1 et bus 0, passager 2) : mettez ces deux personnes dans les pièces 2 et 3. La ligne diagonale suivante rencontre trois personnes : mettez-les dans les trois pièces vides suivantes, 4, 5, 6. En continuant ce schéma, nous finirons par attribuer une chambre à chacune des personnes qui se tiennent patiemment sur le parking.
Pouvons-nous aller plus loin dans l’infini, plus loin qu’une infinité de bus infinis ? Oui, nous pouvons : imaginez que juste à côté de l’hôtel d’Hilbert se trouve un parking. Au premier étage, juste à côté de la porte de l’hôtel, se trouvent nos infiniment nombreux bus infinis déjà connus. Mais nous remarquons ensuite que le garage a une infinité d’étages, chacun avec une infinité de bus infinis. L’hôtel de Hilbert peut-il gérer cette nouvelle couche d’infini ? La réponse est oui ! Vous pouvez imaginer utiliser la méthode précédente pour créer une file unique de passagers à chaque étage du parking, puis demander à chaque file unique de monter dans un bus infini. Maintenant, nous avons ramené le problème à une infinité de bus infinis, dont nous savons qu’ils peuvent être logés dans l’hôtel.
Et si nous ajoutons une autre couche d’infini ? Par exemple, s’il y a une infinité de parkings, chacun avec une infinité d’étages, chaque étage avec une infinité de bus, chaque bus avec une infinité de passagers ? Cela fait quatre couches d’infini, et la réponse est toujours oui ! En fait, la réponse est oui même pour quatre mille couches d’infini. Cela s’arrête-t-il un jour ? L’hôtel de Hilbert ne peut-il jamais accueillir de nouveaux clients ? Y a-t-il un infini trop grand pour l’hôtel de Hilbert ?
Oui, il y en a un. En effet, si nous avions une infinité de couches d’infini, il serait impossible de loger tous ces gens dans l’hôtel de Hilbert. Alors … que se passe-t-il ? Il s’avère que tous les infinis décrits, jusqu’à ce dernier, sont de la même taille. Cette taille est appelée ℵ0 (aleph nought), la taille de l’ensemble ℕ = {1, 2, 3, 4, … } et le nombre de chambres de l’hôtel de Hilbert. C’est Georg Cantor qui, en 1874, a introduit l’idée de comparer les tailles des infinis et a montré qu’il existe des infinis de tailles différentes. Plusieurs mathématiciens importants (Poincaré, Kronecker et, plus tard, Weyl) se sont vivement opposés à ses idées, de même que certains théologiens – qui prétendaient que les idées de Cantor remettaient en cause l’unicité de l’infinité absolue de Dieu. Hilbert, en revanche, a soutenu et défendu Cantor.
Comparer les tailles d’ensembles infinis n’est pas si différent de comparer les tailles d’ensembles finis : pour savoir s’il y a plus de chaises ou plus de personnes dans une salle de conférence, vous n’avez pas besoin de compter les personnes et les chaises et de comparer les deux nombres. Il suffit de regarder la salle et de voir s’il y a des chaises vides (plus de chaises que de personnes) ou des personnes debout (plus de personnes que de chaises) : si chaque personne est assise sur une chaise et qu’il n’y a pas de chaises vides, alors l’ensemble des chaises et l’ensemble des personnes ont la même taille. De même, si chaque passager des bus se voit attribuer une chambre dans l’hôtel de Hilbert et qu’aucune chambre ne reste vide, alors l’ensemble des passagers est une infinité de même taille que l’ensemble des chambres de l’hôtel de Hilbert, ℵ0. Cantor a utilisé cette idée pour montrer que l’ensemble des nombres réels, ℝ, est strictement plus grand que l’ensemble des nombres naturels, ℕ ; son bel argument est devenu connu sous le nom de » diagonale de Cantor. » Cantor a également conjecturé – et tenté de prouver mais sans succès – l’hypothèse du continuum : qu’il n’existe pas d’ensemble infini strictement plus grand que ℕ mais strictement plus petit que ℝ. Hilbert a inclus la preuve de la véracité ou de la fausseté de cette affirmation comme premier problème de la célèbre liste de vingt-trois problèmes qu’il a présentée au Congrès international des mathématiciens de 1900 à Paris, qui allait façonner l’orientation de la recherche en mathématiques pour les décennies à venir. La réponse est que cette hypothèse ne peut pas être prouvée fausse (Gödel, années 1940) mais elle ne peut pas non plus être prouvée vraie (Cohen, années 1960) : c’est un problème indécidable !
Hilbert a dit de façon célèbre, à propos des idées de Cantor sur l’infini et de toutes les nouvelles mathématiques qu’elles ont engendrées : « Personne ne nous chassera du paradis que Cantor a créé. »