Gościnność w hotelu Hilberta
Na początku dwudziestego wieku Uniwersytet w Getyndze był jednym z najlepszych ośrodków badawczych matematyki na świecie. Matematyk David Hilbert był tam uznanym profesorem i w semestrze zimowym 1924-25 wygłosił serię wykładów o nieskończoności w matematyce, fizyce i astronomii. (Te i inne wykłady Hilberta są obecnie opublikowane w formie książkowej przez Springer-Verlag. Książka jest dostępna w bibliotece IAS w tłumaczeniu i w oryginalnej wersji niemieckiej). W jednym z tych wykładów Hilbert posłużył się przykładem, aby wyjaśnić zasadniczą różnicę między zbiorami skończonymi i nieskończonymi: w hotelu o skończonej liczbie pokoi, jeśli wszystkie pokoje są zajęte, to nie ma miejsca dla nowych gości. Ale w hotelu z nieskończenie wieloma pokojami nie stanowi to problemu: jeśli wszystkie pokoje są zajęte, a przyjeżdża nowy gość, wystarczy przenieść każdego starego gościa o jeden pokój dalej, pozostawiając pierwszy pokój wolny dla nowo przybyłego gościa. Podobny argument pozwala nam pomieścić dowolną skończoną liczbę, a nawet nieskończenie wielu nowo przybyłych gości.
George Gamow (autor słynnej pracy Alpher-Bethe-Gamow w dziedzinie kosmologii fizycznej) był letnim postdocem na Uniwersytecie w Getyndze kilka lat po tych wykładach i prawdopodobnie poznał tam przykład nieskończonego hotelu Hilberta. Spopularyzował go w swojej popularnonaukowej książce z 1947 roku zatytułowanej One Two Three…Infinity: Facts and Speculations of Science (dostępna w bibliotece Princeton University).
Powróćmy do hotelu Hilberta. Aby wszystko było jasne, powiedzmy, że nieskończenie wiele pokoi w hotelu ma numery 1, 2, 3, 4, 5, … . Pewnej nocy wszystkie są zajęte, ale przyjeżdża nowy gość. Jak powiedzieliśmy wcześniej, po prostu przenosimy gościa z pokoju 1 do pokoju 2, tego z pokoju 2 do pokoju 3, tego z pokoju 3 do pokoju 4, i ogólnie rzecz biorąc, gościa z pokoju n do pokoju n + 1, tworząc w ten sposób wolne miejsce w pokoju 1 dla nowego gościa, ale nie pozostawiając żadnego z oryginalnych gości bez domu.
Teraz powiedzmy, że przybyło dwudziestu nowych gości, a nie tylko jeden. Sztuczka użyta wcześniej działa równie dobrze: przenieś gościa w pokoju 1 do pokoju 21, gościa w pokoju 2 do pokoju 22, a ogólnie rzecz biorąc, gościa w pokoju n do pokoju n + 20. To pozostawi dwadzieścia pokoi wolnych i gotowych dla dwudziestu nowych gości.
Ale co jeśli nieskończenie wielu nowych gości przybywa na pokładzie nieskończonego autobusu? Możemy zmodyfikować poprzedni argument tak, że nadal działa dla tej sytuacji: rozmieść gości już w hotelu tak, że zajmują tylko co drugi pokój. Mówiąc matematycznie, przenieś gościa z pokoju n do pokoju 2n, tak aby wszystkie pokoje o numerach parzystych były zajęte. Pozostawia to każdy inny pokój (nieskończenie wiele!) wolny i gotowy na przyjęcie (nieskończenie wiele!) osób przyjeżdżających autobusem. Osoba siedząca na miejscu numer n w autobusie powinna przenieść się do n-tego nieparzyście numerowanego pokoju, który jest pokojem numer 2n – 1.
Co jeśli dziewięćdziesiąt dziewięć nieskończonych autobusów przyjeżdża? Po prostu przenieś oryginalnych gości hotelowych do pokoi 100, 200, 300, etc., pasażerów pierwszego autobusu do pokoi 1, 101, 201, etc., pasażerów drugiego autobusu do pokoi 2, 102, 202, etc., i tak dalej dla reszty autobusów. W ten sposób zostaną zajęte wszystkie pokoje w hotelu, a jednocześnie żaden z gości nie pozostanie bez pokoju. Jeśli pasażerowie autobusów sami byliby ponumerowani 1, 2, 3, 4, 5, …. (i nie róbmy rozróżnienia i nazwijmy oryginalnych gości hotelu pasażerami, jak również możemy myśleć o tym jako o przeniesieniu wszystkich oryginalnych gości z hotelu i do ozdobnego autobusu zaparkowanego tuż przed hotelem, który możemy nazwać autobusem numer 0), wtedy zobaczylibyśmy, że pierwsze sto pokoi w hotelu jest wypełnione pasażerami numer 1, drugie sto pokoi w hotelu jest wypełnione pasażerami numer 2, i tak dalej.
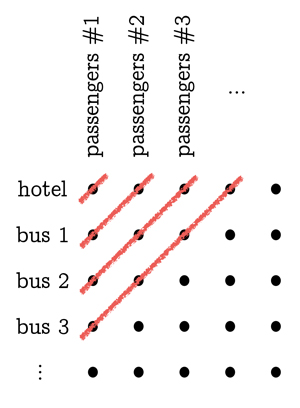
Następny poziom to radzenie sobie z nieskończenie wieloma nieskończonymi autobusami (każdy autobus z nieskończenie wieloma pasażerami). Pierwszą rzeczą, którą należy zrobić, to wydostać wszystkich z hotelu i z autobusów i zorganizować ich w formie siatki na parkingu lub na kartce papieru: niech pierwotni goście hotelu (np. pasażerowie autobusu nr 0) ustawią się w kolejności od lewej do prawej, tworząc rząd. Niech pasażerowie z pierwszego autobusu ustawią się w rzędzie tuż pod nim, a pasażerowie z drugiego autobusu w rzędzie pod nim, itd. Ustaw rzędy tak, aby pasażerowie z numerem 1 z każdego autobusu ustawili się w kolumnie, pasażerowie z numerem 2 w kolumnie na prawo od niej, itd. Teraz, jeśli zaczniemy zapełniać pokoje hotelowe 1, 2, 3, 4, … ludźmi z pierwszego rzędu, nigdy go nie skończymy i przejdziemy do drugiego rzędu, i podobnie, jeśli spróbujemy zacząć od pierwszej kolumny. Sztuczka polega na tym, aby pomyśleć o ukośnych liniach, biegnących z dołu do góry na lewo i z góry na prawo na siatce. Najbardziej wysunięta na lewo z tych ukośnych linii trafia tylko w jedną osobę na górze po lewej stronie (autobus 0, pasażer 1): umieść tę osobę w pokoju 1. Następna ukośna linia trafia w dwie osoby (autobus 1, pasażer 1 i autobus 0, pasażer 2): umieść te dwie osoby w pokojach 2 i 3. Następna linia ukośna trafia na trzy osoby: umieść je w kolejnych trzech pustych pokojach, 4, 5, 6. Kontynuując ten wzór, w końcu przydzielimy pokój każdemu z ludzi cierpliwie stojących na parkingu.
Czy możemy pójść głębiej w nieskończoność, głębiej niż nieskończenie wiele nieskończonych autobusów? Tak, możemy: wyobraźmy sobie, że tuż obok hotelu Hilberta znajduje się parking. Na pierwszym piętrze, tuż przy drzwiach hotelu, stoi nasz znany już nieskończenie wiele nieskończonych autobusów. Ale potem zauważamy: garaż ma nieskończenie wiele pięter, a na każdym z nich nieskończenie wiele nieskończonych autobusów. Czy hotel Hilberta poradzi sobie z tą dodatkową warstwą nieskończoności? Odpowiedź brzmi: tak! Możesz sobie wyobrazić użycie poprzedniej metody, aby zrobić pojedynczy plik pasażerów na każdym piętrze garażu, a następnie powiedzieć każdemu pojedynczemu plikowi, aby wszedł do jednego nieskończonego autobusu. Teraz zmniejszyliśmy problem z powrotem do nieskończenie wielu nieskończonych autobusów, które wiemy, że mogą być zakwaterowane w hotelu.
Co jeśli dodamy kolejną warstwę nieskończoności? Na przykład, jeśli istnieje nieskończenie wiele garaży parkingowych, każdy z nieskończenie wieloma piętrami, każde piętro z nieskończenie wieloma autobusami, każdy autobus z nieskończenie wieloma pasażerami? To są cztery warstwy nieskończoności, a odpowiedź wciąż brzmi tak! W rzeczywistości, odpowiedź jest twierdząca nawet dla czterech tysięcy warstw nieskończoności. Czy to się kiedykolwiek zatrzyma? Czy hotel Hilberta nie jest w stanie przyjąć nowych gości? Czy istnieje nieskończoność, która jest zbyt duża dla hotelu Hilberta?
Tak, istnieje. W rzeczy samej, gdybyśmy mieli nieskończenie wiele warstw nieskończoności, wszyscy ci ludzie nie mogliby być zakwaterowani w hotelu Hilberta. Więc …co się dzieje? Okazuje się, że wszystkie opisane nieskończoności, aż do tej ostatniej, mają ten sam rozmiar. Wielkość ta nazywa się ℵ0 (alef nought), jest to wielkość zbioru ℕ = {1, 2, 3, 4, …} i tyle jest pokoi w hotelu Hilberta. To Georg Cantor w 1874 roku wprowadził pomysł, jak porównywać wielkości nieskończoności i pokazał, że istnieją nieskończoności o różnych wielkościach. Kilku ważnych matematyków (Poincaré, Kronecker, a później Weyl) ostro sprzeciwiało się jego pomysłom, podobnie jak niektórzy teologowie – twierdzili oni, że pomysły Cantora podważają wyjątkowość absolutnej nieskończoności Boga. Hilbert, z drugiej strony, wspierał i bronił Cantora.
Porównywanie rozmiarów zbiorów nieskończonych nie różni się tak bardzo od porównywania rozmiarów zbiorów skończonych: aby wiedzieć, czy w sali wykładowej jest więcej krzeseł czy więcej ludzi, nie trzeba liczyć ludzi i krzeseł i porównywać tych dwóch liczb. Można po prostu rzucić okiem na salę i zobaczyć, czy są puste krzesła (więcej krzeseł niż ludzi) lub ludzie stojący (więcej ludzi niż krzeseł): jeśli każda osoba siedzi na krześle i nie ma pustych krzeseł, to zbiór krzeseł i zbiór ludzi są tej samej wielkości. Podobnie, jeśli każdemu pasażerowi autobusu zostanie przydzielony pokój w hotelu Hilberta i żaden pokój nie pozostanie pusty, to zbiór pasażerów jest nieskończonością o tym samym rozmiarze co zbiór pokoi w hotelu Hilberta, ℵ0. Cantor wykorzystał tę ideę, by pokazać, że zbiór liczb rzeczywistych ℝ jest ściśle większy od zbioru liczb naturalnych ℕ; jego piękny wywód stał się znany jako „przekątna Cantora”. Cantor wysunął też przypuszczenie – i próbował je udowodnić, ale nie udało mu się – że nie istnieje nieskończony zbiór ściśle większy od ℕ, ale ściśle mniejszy od ℝ. Udowodnienie prawdziwości lub fałszywości tego twierdzenia Hilbert umieścił jako pierwszy problem na słynnej liście dwudziestu trzech problemów, którą przedstawił na Międzynarodowym Kongresie Matematyków w Paryżu w 1900 roku, a która miała kształtować kierunek badań matematycznych przez następne dziesięciolecia. Odpowiedź brzmi: hipotezy tej nie można udowodnić, że jest fałszywa (Gödel, lata czterdzieste XX wieku), ale nie można też udowodnić, że jest prawdziwa (Cohen, lata sześćdziesiąte XX wieku): jest to problem niedecydowalny!
Hilbert sławnie powiedział, o ideach Cantora dotyczących nieskończoności i całej nowej matematyce, którą przyniosły: „Nikt nas nie wyrzuci z raju, który stworzył Cantor”
.