Quantenmechanik
Terminologie
Physikalische Systeme werden nach ihren unveränderlichen (oder „zustandsunabhängigen“) Eigenschaften in Typen eingeteilt, und der Zustand eines Systems zu einem bestimmten Zeitpunkt besteht aus einer vollständigen Spezifikation derjenigen seiner Eigenschaften, die sich mit der Zeit ändern (seine „zustandsabhängigen“ Eigenschaften). Um ein System vollständig zu beschreiben, müssen wir also sagen, um welche Art von System es sich handelt und wie sein Zustand zu jedem Zeitpunkt seiner Geschichte ist.
Eine physikalische Größe ist eine sich gegenseitig ausschließende und gemeinsam erschöpfende Familie von physikalischen Eigenschaften (für diejenigen, die diese Redeweise kennen, ist es eine Familie von Eigenschaften mit der Struktur der Zellen in einer Partition). Wenn wir wissen, welche Werte eine Menge annimmt, können wir viel über die Beziehungen zwischen den Eigenschaften, aus denen sie besteht, erfahren. Die Werte einer zweiwertigen Menge bilden beispielsweise eine Menge mit zwei Mitgliedern; die Werte einer reellen Menge bilden eine Menge mit der Struktur der reellen Zahlen. Dies ist ein spezieller Fall von etwas, das wir immer wieder sehen werden, nämlich,dass das Wissen, welche Art von mathematischen Objekten die Elemente in einer Menge repräsentieren (hier die Werte einer physikalischen Größe; später die Zustände, die ein System annehmen kann, oder die zu ihm gehörenden Größen), uns sehr viel (ja, wohl alles, was es zu wissen gibt) über die Beziehungen zwischen ihnen verrät.
In quantenmechanischen Zusammenhängen wird der Begriff „beobachtbar“ austauschbar mit „physikalische Größe“ verwendet und sollte als Fachbegriff mit derselben Bedeutung behandelt werden. Es ist kein Zufall, dass die frühen Entwickler der Theorie diesen Begriff wählten, aber die Wahl wurde aus Gründen getroffen, die heute nicht mehr allgemein anerkannt sind. Der Zustandsraum eines Systems ist der Raum, der durch die Menge seiner möglichen Zustände gebildet wird, d. h. die physikalisch möglichen Kombinationsmöglichkeiten der Werte von Größen, die das System intern charakterisieren. In klassischen Theorien wird eine Menge von Größen, die eine Supervenienzbasis für den Rest bildet, typischerweise als „grundlegend“ oder „fundamental“ bezeichnet, und da jede mathematisch mögliche Art der Kombination ihrer Werte eine physikalische Möglichkeit darstellt, kann der Zustandsraum einfach dadurch erhalten werden, dass man diese als Koordinaten nimmt. So ist beispielsweise der Zustandsraum eines klassischen mechanischen Systems, das aus \(n\) Teilchen besteht und durch die Angabe der Werte von\(6n\) reellwertigen Größen – drei Positionskomponenten und drei Impulskomponenten für jedes Teilchen des Systems – erhalten wird, ein\(6n\)-dimensionaler Koordinatenraum. Jeder mögliche Zustand eines solchen Systems entspricht einem Punkt in diesem Raum, und jeder Punkt in diesem Raum entspricht einem möglichen Zustand eines solchen Systems. In der Quantenmechanik ist die Situation etwas anders, denn hier gibt es mathematisch beschreibbare Möglichkeiten, die Werte der Mengen zu kombinieren, die keine physikalisch möglichen Zustände darstellen. Wie wir sehen werden, handelt es sich bei den Zustandsräumen der Quantenmechanik um spezielle Arten von Vektorräumen, die als Hilbert-Räume bezeichnet werden, und sie haben mehr innere Struktur als ihre klassischen Gegenstücke.
Eine Struktur ist eine Menge von Elementen, auf denen bestimmte Operationen und Beziehungen definiert sind, eine mathematische Struktur ist einfach eine Struktur, in der die Elemente mathematische Objekte (Zahlen, Mengen, Vektoren) und die Operationen mathematische sind, und ein Modell ist eine mathematische Struktur, die verwendet wird, um eine physikalisch bedeutsame Struktur in der Welt darzustellen.
Das Herz und die Seele der Quantenmechanik sind in den Hilberts-Räumen enthalten, die die Zustandsräume quantenmechanischer Systeme darstellen: die internen Beziehungen zwischen den Zuständen und Mengen und alles, was dies über das Verhalten quantenmechanischer Systeme aussagt, sind in die Struktur dieser Räume eingewoben, verkörpert durch die Beziehungen zwischen den mathematischen Objekten, die sie darstellen. Das bedeutet, dass das Verständnis, wie sich ein System gemäß der Quantenmechanik verhält, untrennbar mit der Kenntnis der internen Struktur dieser Räume verbunden ist. Wenn man sich im Hilbert-Raum auskennt und mit den dynamischen Gesetzen vertraut ist, die die Wege beschreiben, die Vektoren durch ihn zurücklegen, dann weiß man alles, was es in den von der Theorie bereitgestellten Begriffen über die Systeme zu wissen gibt, die sie beschreibt.
Mit „sich im Hilbert-Raum auskennen“ meine ich etwas mehr als nur eine Beschreibung oder eine Karte davon zu besitzen; jeder, der ein Lehrbuch der Quantenmechanik in seinem Regal stehen hat, weiß das. Ich meine, dass man sich in ihm auskennt, so wie man sich in der Stadt, in der man lebt, auskennt. Dies ist eine praktische Art von Wissen, das man sich schrittweise aneignet und am besten dadurch, dass man lernt, Probleme dieser Art zu lösen: Wie komme ich von A nach B? Kann ich dorthin gelangen, ohne durch C zu fahren? Und was ist der kürzeste Weg? Doktoranden der Physik verbringen lange Jahre damit, sich mit den Ecken und Winkeln des Hilbert-Raums vertraut zu machen, vertraute Orientierungspunkte zu finden, die ausgetretenen Pfade zu beschreiten, zu lernen, wo Geheimgänge und Sackgassen liegen, und ein Gefühl für die Gesamtlage des Landes zu entwickeln. Sie lernen, sich im Hilbert-Raum zurechtzufinden, so wie ein Taxifahrer lernt, sich in seiner Stadt zurechtzufinden.
Wie viel von dieser Art von Wissen ist erforderlich, um die mit der Theorie verbundenen philosophischen Probleme anzugehen? Am Anfang nicht sehr viel: nur die allgemeinsten Fakten über die Geometrie der Landschaft (die im Gegensatz zu der der meisten Städte sehr schön organisiert ist) und die Wege, die (die Vektoren, die die Zustände der) Systeme durch sie hindurchgehen. Das ist es, was hier eingeführt wird: zuerst ein bisschen einfache Mathematik, und dann, in Kürze, die Theorie.
Mathematik
2.1 Vektoren und Vektorräume
Ein Vektor \(A\), geschrieben ‚\(\ket{A}\)‘, ist ein mathematisches Objekt, das durch eine Länge, \(|A|\), und eine Richtung gekennzeichnet ist. Ein normalisierter Vektor ist ein Vektor der Länge 1, d. h. \(|A| = 1\). Vektoren können addiert, mit Konstanten (einschließlich komplexer Zahlen) multipliziert und miteinander multipliziert werden. Die Vektoraddition bildet ein beliebiges Vektorpaar auf einen anderen Vektor ab, und zwar auf den Vektor, den man erhält, wenn man den zweiten Vektor so verschiebt, dass sein Ende mit der Spitze des ersten zusammenfällt, ohne die Länge oder Richtung eines der beiden Vektoren zu ändern, und dann das Ende des ersten Vektors an die Spitze des zweiten anschließt. Diese Additionsregel ist als Parallelogrammgesetz bekannt. So ergibt beispielsweise die Addition der Vektoren \(\ket{A}\) und \(\ket{B}\) den Vektor \(\ket{C} (= \ket{A} + \ket{B})\) wiein Abbildung 1:
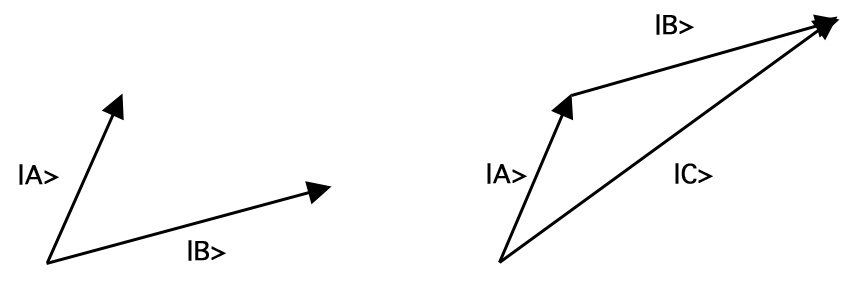
Abbildung 1.Vektoraddition
Multipliziert man einen Vektor \(\ket{A}\) mit \(n\), wobei \(n\) eine Konstante ist, so erhält man einen Vektor, der die gleiche Richtung hat wie \(\ket{A}\), dessen Länge aber \(n\) mal die Länge von \(\ket{A}\) ist.
In einem reellen Vektorraum ist das (innere oder Punkt-)Produkt eines Paares von Vektoren \(\ket{A}\) und \(\ket{B}\), geschrieben’\(\braket{A}{B}\)‘, ein Skalar gleich dem Produkt ihrer Längen (oder ‚Normen‘) mal dem Kosinus des Winkels,\(\theta\), zwischen ihnen:
\
Lassen Sie \(\ket{A_1}\) und \(\ket{A_2}\) Vektoren der Länge 1 („Einheitsvektoren“) sein, so dass \(\braket{A_1}{A_2} = 0\). (Der Winkel zwischen diesen beiden Einheitsvektoren muss 90 Grad betragen.) Dann können wir jeden zweidimensionalen Vektor \(\ket{B}\) in Form unserer Einheitsvektoren wie folgt darstellen:
\
Das folgende Diagramm zeigt zum Beispiel, wie \(\ket{B}\) als Summe der beiden Einheitsvektoren \(\ket{A_1}\) und \(\ket{A_2}\) dargestellt werden kann:
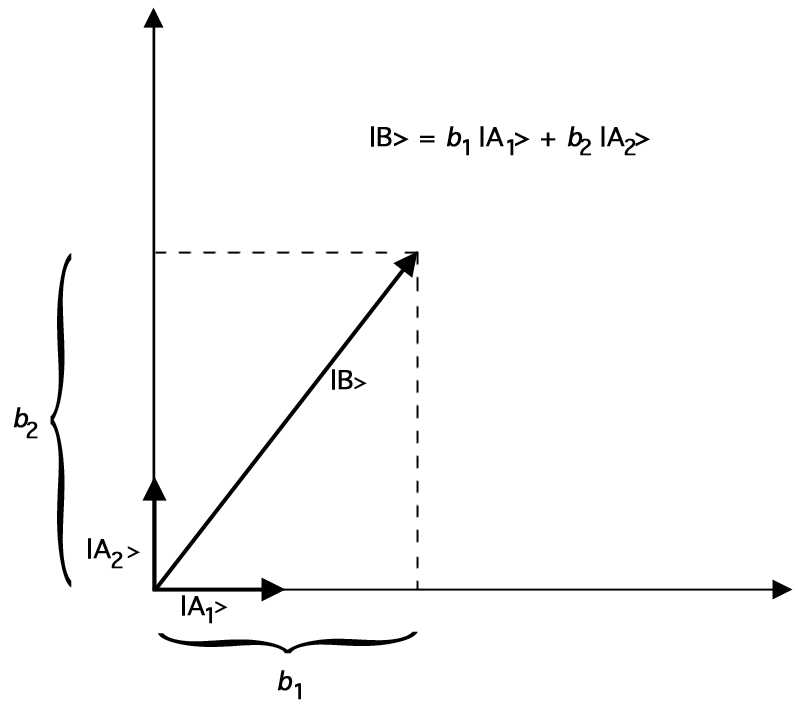
Abbildung 2.Darstellung von \(\ket{B}\) durch Vektoraddition von Einheitsvektoren
Nun muss die Definition des inneren Produkts \(\braket{A}{B}\) modifiziert werden, um sie auf komplexe Räume anzuwenden. Sei \(c^*\) das komplexe Konjugat von \(c\). (Wenn \(c\) eine komplexe Zahl der Form \(a \pm bi\) ist, dann ist das komplex Konjugierte\(c^*\) von \(c\) wie folgt definiert:
\^* = a-bi \\^* = a+bi\]
So ist für alle komplexen Zahlen \(c\), \(^* = c\), aber \(c^* = c\) nur für den Fall, dass \(c\) reell ist.) Die Definition des inneren Produkts von \(\ket{A}\) und \(\ket{B}\) für komplexe Räume kann nun wie folgt in Form der Konjugierten der komplexen Koeffizienten angegeben werden. Wobei \(\ket{A_1}\) und \(\ket{A_2}\) die zuvor beschriebenen Einheitsvektoren sind, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}\) und \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}\), dann
\
Der allgemeinste und abstrakteste Begriff eines inneren Produkts, von dem wir jetzt zwei Spezialfälle definiert haben, ist der folgende. \(\braket{A}{B}\) ist ein inneres Produkt auf einem Vektorraum \(V\) nur für den Fall
- \(\braket{A}{A} = |A|^2\), und \(\braket{A}{A}=0\) wenn und nur wenn \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}^*\)
- \(\braket{B}{A+C}=\braket{B}{A} + \braket{B}{C}\).
Daraus folgt, dass
- die Länge von \(\ket{A}\) die Quadratwurzel des Innenprodukts von \(\ket{A}\) mit sich selbst ist, d.h.,\
und
- \(\ket{A}\) und \(\ket{B}\) sind zueinander senkrecht oder orthogonal, wenn, und nur wenn, \(\braket{A}{B}\).
Ein Vektorraum ist eine Menge von Vektoren, die unter Addition und Multiplikation mit Konstanten geschlossen ist, ein Raum mit innerem Produkt ist ein Vektorraum, auf dem die Operation der Vektormultiplikation definiert ist, und die Dimension eines solchen Raums ist die maximale Anzahl von orthogonalen Vektoren ungleich Null, die er enthält.
Jede Sammlung von \(N\) zueinander orthogonalen Vektoren der Länge 1 in einem\(N\)-dimensionalen Vektorraum bildet eine Orthonormalbasis für diesen Raum. Sei \(\ket{A_1}, \ldots, \ket{A_N}\) eine solche Sammlung von Einheitsvektoren. Dann kann jeder Vektor in diesem Raum als eine Summe der Form:
\
ausgedrückt werden, wobei \(b_i = \braket{B}{A_i}\). Die \(b_i\)’s sind hier als \(B\)’s Expansionskoeffizienten in der \(A\)-Basis bekannt.
Beachte das:
- für alle Vektoren \(A\), \(B\) und \(C\) in einem gegebenen Raum,\
- für alle Vektoren \(M\) und \(Q\), ausgedrückt in der \(A\)-Basis,\
und
\
Es gibt noch eine andere Art, Vektoren zu schreiben, nämlich indem man die Expansionskoeffizienten (relativ zu einer gegebenen Basis) in eine Spalte schreibt, wie z.B.:
\
wobei \(q_i = \braket{Q}{A_i}\) und \(A_i\) die gewählten Basisvektoren sind.
Wenn wir es mit Vektorräumen von unendlicher Dimension zu tun haben, können wir nicht die gesamte Spalte der Expansionskoeffizienten aufschreiben, die für einen Vektor benötigt wird, da sie unendlich lang sein müsste, also schreiben wir stattdessen die Funktion auf (die für \(Q\) als „Wellenfunktion“ bezeichnet wird, gewöhnlich dargestellt als \(\psi(i))\), die diese Koeffizienten als Werte hat. Wir schreiben also die Funktion auf:
\
Gibt man einen beliebigen Vektor in einem Vektorraum und eine beliebige Basis dafür, so erhält man die Wellenfunktion des Vektors in dieser Basis; und gibt man eine Wellenfunktion für einen Vektor in einer bestimmten Basis an, so kann man den Vektor konstruieren, dessen Wellenfunktion er ist. Da sich herausstellt, dass die meisten wichtigen Operationen an Vektoren einfachen algebraischen Operationen an ihren Wellenfunktionen entsprechen, ist dies der übliche Weg zur Darstellung von Zustandsvektoren.
Wenn zwei physikalische Systeme miteinander interagieren, bilden sie ein zusammengesetztes System, und in der Quantenmechanik wie in der klassischen Mechanik gibt es eine Regel, um den Zustandsraum eines zusammengesetzten Systems aus dem seiner Komponenten zu konstruieren, eine Regel, die uns sagt, wie wir aus den Zustandsräumen \(H_A\) und \(H_B\) für \(A\) bzw. \(B\) den Zustandsraum – das so genannte „Tensorprodukt“ von \(H_A\) und \(H_B\) – des Paares erhalten können, und die geschrieben wird (H_A mal H_B\). Diese Regel ist in zweierlei Hinsicht wichtig: Erstens ist \(H_A\) und \(H_B\) ein Hilbert-Raum, solange es sich um Hilbert-Räume handelt, und zweitens gibt es einige Fakten über die Art und Weise, wie sich \(H_A \otimes H_B\) zu \(H_A\) und \(H_B\) verhält, die überraschende Konsequenzen für die Beziehungen zwischen dem komplexen System und seinen Teilen haben. Insbesondere stellt sich heraus, dass der Zustand eines zusammengesetzten Systems nicht eindeutig durch die Zustände seiner Komponenten definiert ist. Das bedeutet, oder zumindest scheint es so, dass es nach der Quantenmechanik Fakten über zusammengesetzte Systeme gibt (und nicht nur Fakten über ihre räumliche Konfiguration), die nicht von Fakten über ihre Komponenten abhängen; es bedeutet, dass es Fakten über Systeme als Ganzes gibt, die nicht von Fakten über ihre Teile und die Art und Weise, wie diese Teile im Raum angeordnet sind, abhängen. Die Bedeutung dieses Merkmals der Theorie kann nicht überbewertet werden; es ist auf die eine oder andere Weise in die meisten ihrer schwierigsten Probleme verwickelt.
Ein wenig ausführlicher: Wenn \(\{v_{i}^A\}) eine orthonormale Basis für \(H_A\) und \(\{u_{j}^B\}) eine orthonormale Basis für \(H_B\) ist, dann wird die Menge der Paare \((v_{i}^A, u_{j}^B)\) als eine orthonormale Basis für den Tensorproduktraum \(H_A \mal H_B\) betrachtet. Für das Paar \((v_{i}^A,u_{j}^B)\) wird die Bezeichnung \(v_i^A,u_{j}^B)\) verwendet, und das innere Produkt auf \(H_A \otimes H_B\) ist definiert als:
\
Es ist ein Ergebnis dieser Konstruktion, dass, obwohl jeder Vektor in \(H_A \mal H_B\) eine lineare Summe von Vektoren ist, die in der Form \(v_{i}^A \mal u^B\) ausgedrückt werden können, nicht jeder Vektor im Raum selbst in dieser Form ausgedrückt werden kann, und es stellt sich heraus, dass
- jeder zusammengesetzte Zustand eindeutig die Zustände seiner Komponenten definiert.
- Wenn die Zustände von \(A\) und \(B\) rein sind (d.h., darstellbar durch die Vektoren \(v^A\) bzw. \(u^B\)), dann ist der Zustand von \((A+B)\) rein und wird dargestellt durch\(v^A \mal u^B\), und
- wenn der Zustand von \((A+B)\) rein ist und in der Form \(v^A \otimes u^B\) ausgedrückt werden kann, dann sind die Zustände von \(A\) und \(B\) rein, aber
- wenn die Zustände von \(A\) und \(B\) nicht rein sind, d. h.e., wenn sie gemischte Zustände sind (diese werden weiter unten definiert), definieren sie nicht eindeutig den Zustand von \((A+B)\); insbesondere kann es ein reiner Zustand sein, der nicht in der Form \(v^A \mal u^B\) ausgedrückt werden kann.
2.2 Operatoren
Ein Operator \(O\) ist eine Abbildung eines Vektorraums auf sich selbst; er überträgt einen beliebigen Vektor \(\ket{B}\) in einem Raum auf einen anderen Vektor \(\ket{B‘}\), der sich ebenfalls in diesem Raum befindet; \(O \ket{B} = \ket{B‘}\). Lineare Operatoren sind Operatoren, die die folgenden Eigenschaften haben:
- \(O(\ket{A} + \ket{B}) = O \ket{A} + O \ket{B}\), und
- \(O(c \ket{A}) = c(O \ket{A})\).
Gleich wie jeder Vektor in einem \(N\)-dimensionalen Raum durch eine Spalte von \(N\)-Zahlen dargestellt werden kann, relativ zu einer gewählten Basis für den Raum, kann jeder lineare Operator auf dem Raum in einer Spaltenschreibweise durch\(N^2\) Zahlen dargestellt werden:
\
wobei \(O_{ij} = \braket{A_i}{O \mid A_j}\) und die \(A_N\) die Basisvektoren des Raumes sind. Die Wirkung des linearen Operators \(O\) auf den Vektor\(B\) ist dann gegeben durch
\
Zwei weitere Definitionen, bevor wir sagen können, was Hilbert-Räume sind, und dann können wir uns der Quantenmechanik zuwenden. \(\ket{B}\) ist ein Eigenvektor von \(O\) mit dem Eigenwert \(a\), wenn, und nur wenn, \(O \ket{B} = a \ket{B}\).Verschiedene Operatoren können verschiedene Eigenvektoren haben, aber die Beziehung zwischen Eigenvektoren und Operator hängt nur von dem betreffenden Operator und den Vektoren ab und nicht von der jeweiligen Basis, in der sie ausgedrückt werden; die Beziehung zwischen Eigenvektoren und Operator ist also invariant bei Änderung der Basis. Ein Hermite’scher Operator ist ein Operator, der die Eigenschaft hat, dass es eine Orthonormalbasis gibt, die aus seinen Eigenvektoren besteht und dass diese Eigenwerte alle real sind.
Ein Hilbert-Raum schließlich ist ein Vektorraum, auf dem ein inneres Produkt definiert ist und der vollständig ist, d.h. so, dass jede Cauchy-Folge von Vektoren im Raum zu einem Vektor im Raum konvergiert. Alle endlich-dimensionalen inneren Produkträume sind vollständig, und ich werde mich auf diese beschränken. Der unendliche Fall bringt einige Komplikationen mit sich, auf die hier nicht eingegangen werden soll.
Quantenmechanik
Vier Grundprinzipien der Quantenmechanik sind:
(3.1)
Physikalische Zustände.Jedes physikalische System ist mit einem Hilbert-Raum assoziiert, jeder Einheitsvektor im Raum entspricht einem möglichen reinen Zustand des Systems und jeder mögliche reine Zustand einem Vektor im Raum.
(3.2)
Physikalische Größen.Hermitsche Operatoren im Hilbert-Raum, der mit einem System assoziiert ist, repräsentieren physikalische Größen, und ihre Eigenwerte repräsentieren die möglichen Ergebnisse von Messungen dieser Größen.
Es gibt einen Operator, den sogenannten Hamiltonian, der in der Quantentheorie eine besondere Rolle spielt, weil die Dynamik eines Systems durch die Verfolgung seiner Entwicklung einfach formuliert werden kann. Der Hamiltonian – geschrieben \(H\), oder \(\hat{H}\) – steht für die Gesamtenergie des Systems. Seine Eigenwerte sind die möglichen Ergebnisse, die bei Messungen der Gesamtenergie erzielt werden können. Sie ergibt sich aus der Summierung der kinetischen und potentiellen Energien der Komponenten des Systems.
(3.3)
Zusammensetzung: Der Hilbertraum eines komplexen Systems ist das Tensorprodukt der Tensorprodukte der einfachen Systeme (in der nichtrelativistischen Standardtheorie: der einzelnen Teilchen), aus denen es sich zusammensetzt.
(3.4) Dynamik. a.
Zusammenhänge des Typs 1: Ausgehend vom Zustand eines Systems zum Zeitpunkt \(t\) und den Kräften und Zwängen, denen es unterworfen ist, gibt es eine Gleichung, die „Schrödingergleichung“, die den Zustand zu jedem anderen Zeitpunkt \(U\ket{v_t} \rightarrow \ket{v_{t‘}}\) liefert. Die für unsere Zwecke wichtigen Eigenschaften von \(U\) sind, dass sie deterministisch ist, d. h., dass sie den Zustand eines Systems zu einem bestimmten Zeitpunkt in einen eindeutigen Zustand zu jedem anderen Zeitpunkt überführt, dass sie unitär ist, d. h., dass sie ein Automorphismus des Hilbert-Raums ist, auf den sie wirkt (d. h., Abbildung dieses Raums auf sich selbst, die die lineare Raumstruktur und das innere Produkt bewahrt), und sie ist linear, d. h., wenn sie einen Zustand \(\ket{A}\) auf den Zustand\(\ket{A‘}\) überträgt, und sie den Zustand \(\ket{B}\) auf den Zustand\(\ket{B‘}\) überträgt, dann überträgt sie jeden Zustand der Form \(\alpha \ket{A} +\beta \ket{B}\) auf den Zustand \(\alpha \ket{A‘} + \beta\ket{B‘}\).
b.
Kontexte vom Typ 2 („Messkontexte“):Die Durchführung einer „Messung“ einer Beobachtungsgröße \(B\) an einem System im Zustand \(\ket{A}\) bewirkt, dass das System in einen \(B\)-Eigenzustand kollabiert, der dem beobachteten Eigenwert entspricht. Dies ist als Kollapspostulat bekannt. In welchen \(B\)-Eigenzustand es kollabiert, ist eine Frage der Wahrscheinlichkeit, und die Wahrscheinlichkeiten sind durch eine Regel gegeben, die als Bornsche Regel bekannt ist:
\
Es gibt zwei wichtige Punkte, die bei diesen beiden Arten von Zusammenhängen zu beachten sind:
- Die Unterscheidung zwischen Kontexten des Typs 1 und 2 ist quantenmechanisch noch nicht geklärt; niemand hat es geschafft, in den Begriffen, die die Theorie zur Verfügung stellt, vollständig zufriedenstellend zu sagen, welche Kontexte Messkontexte sind, und
- Selbst wenn die Unterscheidung geklärt ist, ist es eine offene Interpretationsfrage, ob es Kontexte des Typs 2 gibt, d. h.e., es ist eine offene Interpretationsfrage, ob es Kontexte gibt, in denen Systeme von einer anderen dynamischen Regel als der Schrödinger-Gleichung beherrscht werden.
Strukturen im Hilbert-Raum
Ich habe oben bemerkt, dass in der gleichen Weise, wie alle Informationen, die wir über die Beziehungen zwischen Orten in einer Stadt haben, in den räumlichen Beziehungen zwischen den Punkten auf einer Karte verkörpert sind, die sie repräsentieren, alle Informationen, die wir über die internen Beziehungen zwischen (und zwischen) Zuständen und Größen in der Quantenmechanik haben, in den mathematischen Beziehungen zwischen den Vektoren und Operatoren verkörpert sind, die sie repräsentieren. Was die Quantenmechanik aus mathematischer Sicht wirklich von ihren klassischen Vorgängern unterscheidet, ist, dass die Zustände und Größen eine reichere Struktur haben; sie bilden Familien mit einem interessanteren Netzwerk von Beziehungen zwischen ihren Mitgliedern.
Alle physikalisch bedeutsamen Merkmale des Verhaltens quantenmechanischer Systeme sind Folgen mathematischer Eigenschaften dieser Beziehungen, und die wichtigsten davon lassen sich leicht zusammenfassen:
(P1)
Jede Art, Vektoren in einem Hilbert-Raum zu addieren oder mit Skalaren zu multiplizieren, ergibt einen Vektor, der ebenfalls in diesem Raum liegt. Ist der Vektor normalisiert, so repräsentiert er nach (3.1) einen möglichen Zustand des Systems, und ist er die Summe eines Paares von Eigenvektoren einer Beobachtungsgröße \(B\) mit unterschiedlichen Eigenwerten, so ist er nicht selbst ein Eigenvektor von \(B\), sondern nach (3.4b) mit einem Satz von Wahrscheinlichkeiten für das eine oder das andere Ergebnis bei \(B\)-Messungen verknüpft.
(P2)
Für jeden hermiteschen Operator auf einem Hilbert-Raum gibt es andere auf demselben Raum, mit denen er keinen vollständigen Satz von Eigenvektoren gemeinsam hat; in der Tat ist es leicht zu zeigen, dass es andere solche Operatoren gibt, mit denen er keine Eigenvektoren gemeinsam hat.
Wenn wir ein paar zusätzliche interpretierende Annahmen machen, können wir mehr sagen. Nehmen wir zum Beispiel an, dass
(4.1)
Jeder hermitesche Operator auf dem Hilbert-Raum, der mit einem System assoziiert ist, eine bestimmte Beobachtung repräsentiert, und (daher) jeder normalisierte Vektor einen bestimmten Zustand, und
(4.2)
Ein System hat einen Wert für die Beobachtung \(A\), wenn, und nur wenn, der Vektor, der seinen Zustand repräsentiert, ein Eigenzustand des \(A\)-Operators ist. Der Wert, den es in einem solchen Fall hat, ist einfach der Eigenwert, der mit diesem Eigenzustand assoziiert ist.
Aus (P2) folgt durch (3.1), dass kein quantenmechanischer Zustand ein Eigenzustand aller Observablen ist (und dass es tatsächlich Observablen gibt, die keine gemeinsamen Eigenzustände haben), und daher, durch (3.2), dass kein quantenmechanisches System jemals gleichzeitige Werte für alle zu ihm gehörenden Größen hat (und dass es sogar Paare von Größen gibt, denen kein Zustand gleichzeitige Werte zuordnet).
Es gibt hermitsche Operatoren auf dem Tensorprodukt\(H_1 \mal H_2\) eines Paares von Hilberträumen\(H_1\) und \(H_2\) … Für den Fall, dass \(H_1\) und \(H_2\) die Zustandsräume der Systeme \(S1\) und \(S2\) sind, ist \(H_1 \mal H_2\) der Zustandsraum des komplexen Systems \((S1+S2)\). Aus (4.1) folgt, dass es zu \((S1+S2)\) gehörende Observablen gibt, deren Werte nicht durch die Werte der zu den beiden gehörenden Observablen bestimmt sind.
Dies sind alles direkte Konsequenzen daraus, dass man Vektoren und Operatoren im Hilbert-Raum nimmt, um Zustände bzw. Observablen zu repräsentieren, und die Bornsche Regel (und später (4.1) und (4.2)) anwendet, um den Zustandszuordnungen empirische Bedeutung zu verleihen. Die eigentliche Schwierigkeit beim Verständnis der Quantenmechanik besteht darin, ihre physikalischen, metaphysischen und erkenntnistheoretischen Implikationen in den Griff zu bekommen.
Jeder, der versucht, zu verstehen, was die Quantenmechanik über die Welt aussagt, muss sich mit einer verbleibenden Tatsache auseinandersetzen. Dieses Problem hat nichts mit Hilbert-Räumen zu tun, sondern mit der Dynamik – den Regeln, die die Bahnen beschreiben, die Systeme durch den Raum ziehen. Aus physikalischer Sicht ist es weitaus problematischer als alles bisher Gesagte. Es stellt nicht nur jemanden vor Schwierigkeiten, der versucht, eine Interpretation der Theorie zu liefern, sondern scheint auch auf eine logische Inkonsistenz in den Grundlagen der Theorie hinzuweisen.
Angenommen, wir haben ein System \(S\) und ein Gerät \(S^*\), das eine Beobachtungsgröße \(A\) auf \(S\) mit Werten \(\{a_1,a_2, a_3, …\}\) misst. Dann gibt es einen Zustand von \(S^*\) (den „Grundzustand“) und eine Beobachtungsgröße \(B\) mit Werten \(\{b_1, b_2,b_3, …\}\), die zu \(S^*\) gehört (seine „Zeiger-Beobachtungsgröße“, so genannt, weil sie die Rolle des Zeigers auf einer Skala an der Vorderseite eines schematischen Messinstruments bei der Registrierung des Ergebnisses des Experiments spielt), die so beschaffen sind, dass, wenn \(S^*\) in seinem Grundzustand gestartet wird und in geeigneter Weise mit \(S\) wechselwirkt, und wenn der Wert von \(A\) unmittelbar vor der Wechselwirkung gleich\(a_1\) ist, der Wert von \(B\) unmittelbar danach gleich\(b_1\) ist. Wenn jedoch der Wert von \(A\) unmittelbar vor der Interaktion \(a_2\) ist, dann ist der Wert von \(B\) unmittelbar danach \(b_2\); wenn der Wert von \(A\) unmittelbar vor der Interaktion \(a_3\) ist, dann ist der Wert von \(B\) unmittelbar danach \(b_3\), und so weiter. Das ist genau das, was es bedeutet, wenn man sagt, dass \(S^*\) \(A\) misst. Wenn wir also den gemeinsamen, partiellen Zustand von \(S\) und \(S^*\) (nur den Teil davon, der den Wert der Beobachtungsgröße spezifiziert, deren Werte den gemeinsamen Zuweisungen von Werten an die gemessene Beobachtungsgröße auf \(S\) und die Zeiger-Beobachtungsgröße auf \(S^*\) entsprechen) durch den Vektor\(\ket{A=a_i}_s \ket{B=b_i}_{s^*}\) darstellen, und lassen wir „\(\rightarrow\)“ für die dynamische Beschreibung der Wechselwirkung zwischen den beiden stehen, so bedeutet die Aussage, dass \(S^*\) ein Messinstrument für \(A\) ist, dass die dynamischen Gesetze dies bedingen,
\
und so weiter.
Intuitiv ist \(S^*\) ein Messinstrument für ein beobachtbares \(A\), wenn es irgendeine beobachtbare Eigenschaft von \(S^*\) gibt (es spielt keine Rolle, was, nur etwas, dessen Werte durch das Betrachten des Geräts festgestellt werden können), die mit den \(A\)-Werten von Systemen, die ihm zugeführt werden, so korreliert ist, dass wir diese Werte aus dem beobachtbaren Zustand von \(S^*\) nach der Interaktion ablesen können. Im philosophischen Sprachgebrauch ist \(S^*\) ein Messinstrument für \(A\), für den Fall, dass es irgendeine beobachtbare Eigenschaft von \(S^*\) gibt, die die \(A\)-Werte von Systemen, mit denen es interagiert, in geeigneter Weise verfolgt oder anzeigt.
Aus (3.1) folgt nun, dass es Zustände von \(S\) gibt (zu viele, um sie aufzuzählen), die keine Eigenzustände von \(A\) sind, und wenn wir betrachten, was die Schrödinger-Gleichung über die gemeinsame Entwicklung von \(S\) und \(S^*\) aussagt, wenn \(S\) in einem dieser Zustände gestartet wird, stellen wir fest, dass der Zustand des Paares nach der Wechselwirkung eine Überlagerung von Eigenzuständen von ist. Es spielt keine Rolle, welche Beobachtungsgröße an \(S\) gemessen wird, und es spielt keine Rolle, in welcher speziellen Überlagerung \(S\) beginnt; wenn es in ein Messgerät für diese Beobachtungsgröße eingespeist wird, wenn die Wechselwirkung korrekt durch die Schrödingersche Sequenz beschrieben wird, folgt allein aus der Linearität des \(U\) in dieser Gleichung, dem Operator, der die Transformation vom früheren zum späteren Zustand des Paares bewirkt, dass der gemeinsame Zustand von \(S\) und dem Gerät nach der Wechselwirkung eine Überlagerung von Eigenzuständen dieser Beobachtungsgröße auf dem gemeinsamen System ist.
Angenommen, wir beginnen \(S^*\) in seinem Grundzustand und \(S\) im Zustand
\
Es ist eine Folge der Regeln zur Gewinnung des Zustandsraums des zusammengesetzten Systems, dass der gemeinsame Zustand des Paares
\
ist, und es folgt aus der Tatsache, dass \(S^*\) ein Messinstrument für \(A\) ist,und der Linearität von \(U\), dass ihr kombinierter Zustand nach der Wechselwirkung
\
ist, ist jedoch unvereinbar mit der dynamischen Regel für Kontexte des Typs 2, denn die dynamische Regel für Kontexte des Typs 2 (und wenn es solche Kontexte gibt, dann ist dies einer) beinhaltet, dass der Zustand des Paares nach der Interaktion entweder
\
oder
\
ist, es bedeutet, dass es eine genaue Wahrscheinlichkeit von \(\frac{1}{2}\) gibt, dass es im ersten Zustand endet, und eine Wahrscheinlichkeit von \(\frac{1}{2}\), dass es im zweiten Zustand endet.
Wir können versuchen, die logische Konsistenz wiederherzustellen, indem wir die dynamische Regel für Kontexte vom Typ 2 aufgeben (oder, was auf dasselbe hinausläuft, indem wir leugnen, dass es solche Kontexte überhaupt gibt), aber dann haben wir das Problem der Konsistenz mit der Erfahrung. Denn es war kein bloßer Fehler, dass diese Regel in die Theorie aufgenommen wurde; wir wissen, wie ein System aussieht, wenn es sich in einem Eigenzustand einer gegebenen Observablen befindet, und wir wissen aus der Anschauung, dass sich der Messapparat nach der Messung in einem Eigenzustand der Zeigerobservablen befindet. Und so wissen wir von Anfang an, dass eine Theorie, die uns etwas anderes über die Zustände der Messgeräte nach der Messung sagt, was auch immer dieses andere ist, falsch ist.
Das ist, kurz gesagt, das Messproblem in der Quantenmechanik; jede Interpretation der Theorie, jede detaillierte Geschichte darüber, wie die Welt nach der Quantenmechanik aussieht, und insbesondere jene Teile der Welt, in denen Messungen stattfinden, muss sich damit auseinandersetzen.
Lose Enden
Gemischte Zustände sind gewichtete Summen reiner Zustände, und sie können verwendet werden, um die Zustände von Ensembles darzustellen, deren Komponenten sich in verschiedenen reinen Zuständen befinden, oder Zustände einzelner Systeme, über die wir nur teilweise Bescheid wissen. Im ersten Fall spiegelt das Gewicht, das einem gegebenen reinen Zustand zugeordnet ist, die Größe der Komponente des Ensembles wider, die sich in diesem Zustand befindet (und damit die objektive Wahrscheinlichkeit, dass ein beliebiges Mitglied des Ensembles sich in diesem Zustand befindet); im zweiten Fall spiegeln sie die epistemische Wahrscheinlichkeit wider, dass sich das fragliche System, dem der Zustand zugeordnet ist, in diesem Zustand befindet.
Wenn wir die Unterscheidung zwischen reinen und gemischten Zuständen nicht verlieren wollen, brauchen wir eine Möglichkeit, die gewichtete Summe einer Menge von reinen Zuständen (äquivalent, der mit ihnen verbundenen Wahrscheinlichkeitsfunktionen) darzustellen, die sich von der Addition der (geeignet gewichteten) Vektoren, die sie repräsentieren, unterscheidet, und das bedeutet, dass wir entweder eine alternative Möglichkeit brauchen, gemischte Zustände darzustellen, oder eine einheitliche Möglichkeit, sowohl reine als auch gemischte Zustände darzustellen, die die Unterscheidung zwischen ihnen bewahrt.In Hilbert-Räumen gibt es eine Art von Operator, den sogenannten Dichteoperator, der sich gut für die letztgenannte Funktion eignet, und es stellt sich heraus, dass es nicht schwer ist, alles, was über Zustandsvektoren gesagt wurde, in Form von Dichteoperatoren wiederzugeben. Obwohl es üblich ist, von reinen Zuständen zu sprechen, die durch Vektoren dargestellt werden, lautet die offizielle Regel, dass Zustände – sowohl reine als auch gemischte – in der Quantenmechanik durch Dichteoperatoren dargestellt werden.
Obwohl gemischte Zustände, wie gesagt, verwendet werden können, um unsere Unkenntnis über die Zustände von Systemen darzustellen, die sich tatsächlich in dem einen oder anderen reinen Zustand befinden, und obwohl dies vielen als eine angemessene Art und Weise erschienen ist, Mischungen in klassischen Zusammenhängen zu interpretieren, gibt es ernsthafte Hindernisse, dies allgemein auf quantenmechanische Mischungen anzuwenden. Diese werden in den anderen Einträgen zur Quantenmechanik in der Enzyklopädie ausführlich erörtert.
Alles, was über Observablen gesagt wurde, gilt streng genommen nur für den Fall, dass die Werte der Observablen eine diskrete Menge bilden; die mathematischen Feinheiten, die erforderlich sind, um sie auf den Fall kontinuierlicher Observablen zu verallgemeinern, sind kompliziert und werfen Probleme eher technischer Natur auf. Auch diese sollten am besten einer ausführlichen Diskussion überlassen werden.
Dies sollte die gesamte anfängliche Vorbereitung sein, die man braucht, um sich der philosophischen Diskussion der Quantenmechanik zu nähern, aber es ist nur ein erster Schritt. Je mehr man über die Beziehungen zwischen Vektoren und Operatoren im Hilbert-Raum, über die Beziehung zwischen den Räumen einfacher Systeme und denen komplexer Systeme und über die Gleichung, die die Bewegung der Zustandsvektoren durch den Raum beschreibt, lernt, desto besser wird man sowohl die Natur als auch die Schwierigkeit der mit der Theorie verbundenen Probleme verstehen. Das Komische an der Quantenmechanik, das, was sie für einen Philosophen unendlich spannend macht, ist, dass die Probleme umso schwieriger werden, je mehr man lernt.