Quantum Mechanics
Terminology
物理システムは、その不変の性質(あるいは「状態非依存性」)によってタイプ分けされており、ある時間におけるシステムの状態は、時間とともに変化する性質(その「状態依存性」)を完全に特定することによって構成されています。 システムの完全な記述を行うには、それがどのようなタイプのシステムであり、その歴史の各瞬間においてどのような状態であるかを言う必要があるのである。
物理量とは、物理的性質の相互排他的かつ共同網羅的な族(この言い方を知っている人は、パーティションのセルの構造を持つ性質の族)である。 ある量がどのような値をとるかを知ることは、その量が構成する性質の関係について多くのことを教えてくれる。 例えば、2価の量の値は2つのメンバーからなる集合を形成し、実数値の量の値は実数の構造を持つ集合を形成する。 これは、私たちが何度も繰り返し見ていることの特別なケースである。量子力学の文脈では、「観測可能」という用語は「物理量」と同じ意味で使われ、同じ意味を持つ専門用語として扱われる必要があります。 この理論の初期の開発者がこの用語を選んだのは偶然ではありませんが、この選択がなされた理由は、現在では一般に受け入れられていないものです。 システムの状態空間とは、そのシステムが取りうる状態の集合によって形成される空間であり、すなわち、そのシステムを内部的に特徴づける量の値の組み合わせの物理的に可能な方法である。 古典的な理論では、残りの量の超越的な基礎を形成する量のセットは、通常、「基本」または「基本」と呼ばれ、その値の組み合わせの数学的に可能な方法はすべて物理的可能性であるので、状態空間はこれらを単に座標として取ることによって得ることができる。 したがって、例えば、実数値の量である位置の3成分、運動量の3成分の値を指定することによって得られる、古典力学系の状態空間がa\(6n)-dimensional座標空間である。 このような系の各可能な状態は、空間内の点に対応し、空間内の各点は、このような系の可能な状態に対応する。 量子力学では少し状況が異なり、物理的に可能な状態を表さない量の値の組み合わせが、数学的に記述可能な方法で存在する。 これから見るように、量子力学の状態空間はヒルベルト空間と呼ばれる特殊なベクトル空間であり、古典的なものよりも内部構造を持っています。
構造は、ある操作と関係が定義されている要素のセットであり、数学構造は、要素が数学的オブジェクト(数、セット、ベクトル)であり操作が数学的である構造であり、モデルは世界内の物理的に重要な構造を表すのに用いられる数学構造であります。
数学
2.1 ベクトルとベクトル空間
ベクトル(A)(「 \ket{A} 」の意)は、長さと方向で特徴づけられる数学的な物体であり、(|A |)であると同時に、(|A)であるとともに、(|A)である。 正規化されたベクトルは長さ1のベクトル、つまり \(|A| = 1ờng) です。 ベクトルには、加算、定数(複素数を含む)乗算、乗算があります。 ベクトル加算は、任意のベクトル対を別のベクトルに写すもので、具体的には、長さや方向を変えずに2番目のベクトルの尾を1番目のベクトルの先端に一致させ、1番目のベクトルの尾を2番目のベクトルの先端に結合したものである。 この足し算の法則は平行四辺形の法則と呼ばれる。 したがって、例えば、ベクトル \(\ket{A}) と( \ket{B}) を足すと、ベクトル \(\ket{C}) ができます。 (= \ket{A} + \ket{B})\) Figure 1:
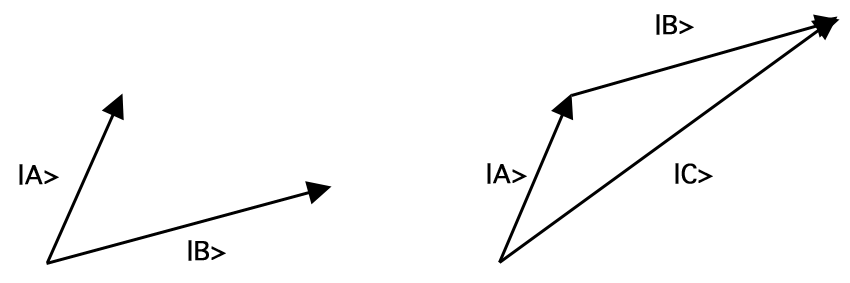
Figure 1.のようになる。ベクトル加算
あるベクトル( \ket{A}) に(n)を掛けると、(n)を定数としたとき、(n)と同じ方向で長さが(n)に(㊟)の倍のベクトルになります。
実数ベクトル空間において、2つのベクトル( \ket{A}, \ket{B}) の内積(ドットプロダクト)は、それらの長さの積にそれらの間の角度のコサイン( \theta\)をかけたスカラーであり、’North’ と呼ばれることがあります。
Ltd. (\ket{A_1}) and \(\ket{A_2}) be vectors of length 1 (“unit vectors”) such that \(braket{A_1}{A_2} = 0ครื่อม). (この2つの単位ベクトルのなす角は90度である。)すると、任意の2次元ベクトルⒶを単位ベクトルで表すと次のようになります。
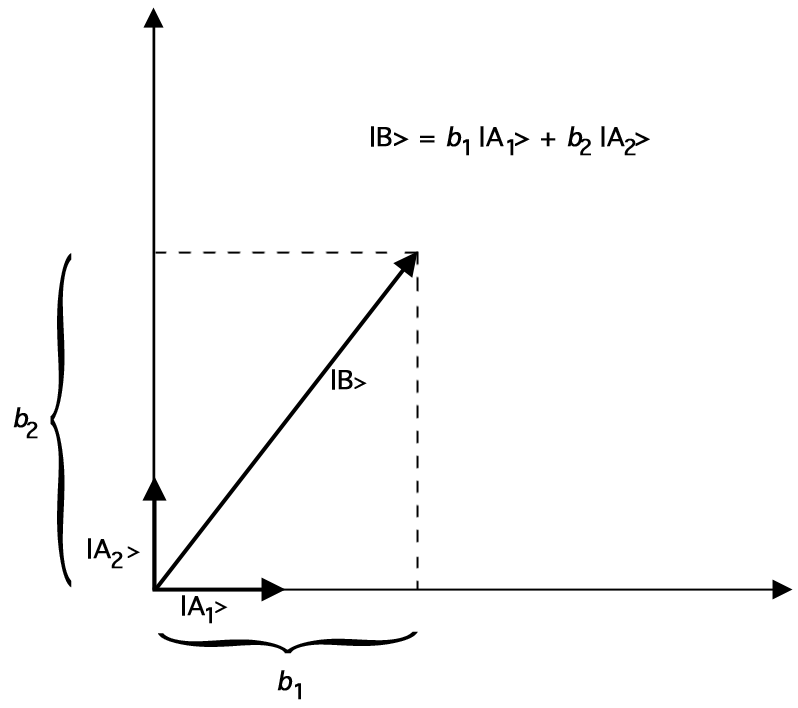
Figure 2.Representing \(\ket{B}) by Vector Addition of Unit Vectors
ここで内積の定義を複素空間に適用するために修正する必要がある。 \(c^*) is the complexconjugate of \(c). (ここで、(C)が複素数の場合、(C)の複素共役(c^*) は次のように定義されます。[
Θ^* = a-bi \^* = a+bi]
したがって、すべての複素数の場合、 \(^* = c)、ただし \(c^* = c) が実数の場合のみ) ここで、複素数空間の内積の定義ですが、複素係数の共役で次のように与えられます。 ここで、♪♪♪は先ほどの単位ベクトル、♪♪♪は(♪♪)=a_1 ♪♪+ a_2 ♪♪♪は(♪♪)、♪♪♪は(♪♪)=b_1 ♪♪+ b_2 ♪♪♪は(♪♪)です。 とすると、
内積の最も一般的で抽象的な概念は、今2つの特殊なケースを定義しましたが、次のようになります。 \braket{A}{B}} = |A|^2} のとき、aninner product on a vector space \(V}) is just in case
- [(\braket{A}{A} = |A|^2} ]。 and \(A=0} if and only if \(A=0})
- \(\braket{B}{A} = \braket{A}{B}^*)
- \(\braket{B}{A+C}=পbraket{B}{A} + \braket{B}{C}) {}.
これより、
- the length of \(\ket{A}) is the square root of innerproduct of \(\ket{A}) with itself, e.g.,,\
ベクトル空間とは、加算と定数による乗算で閉じたベクトルの集合であり、内積空間とはベクトルの乗算が定義されたベクトル空間であり、その空間の次元とは0以外の互いに直交するベクトルの最大個数である。
Any collection of \(N) mutually orthogonal vectors of length 1 in an(N)dimensional vector space constitutes an orthonormalbasis for that space.これは、ある次元ベクトル空間において、長さ1の互いに直交するベクトル(gucci)の任意の集まりである。 このような単位ベクトルの集まりを \(\ket{A_1}, \ldots, \ket{A_N}) とすると、以下のようになります。 すると、空間内のすべてのベクトルは次のような和で表現されます:
ここで、 \(b_i = \braket{B}{A_i}) ここでいう \(b_i) は \(B) の展開係数のA面における値です。
Notice that:
- for all vectors \(A), \(B), and \(C) in a given space, \
- for any vectors \(M) and \(Q), expressed in terms of the \(A)-basis,\ ベクトルにはもう一つの書き方があって、それは展開係数を(与えられた基底に対して)列で書くことである。
無限次元のベクトル空間を扱う場合、ベクトルを取り出すのに必要な展開係数の列を全部書くと無限に長くなるので、代わりにその係数を値として持つ関数(Thomas(Q)は「波動関数」といい、通常 \(psi(i))\ と表す)を書き下ろします。 あるベクトル空間の任意のベクトルとその基底が与えられると、その基底におけるそのベクトルの波動関数が得られます。また、ある基底におけるあるベクトルの波動関数が与えられると、その波動関数のベクトルを構成できます。 ベクトルに対する重要な操作のほとんどは、その波動関数に対する簡単な代数操作に対応することが判明したので、これは状態ベクトルを表現する通常の方法です。
物理システムのペアが相互作用するとき、それらは複合システムを形成します。古典力学と同様に量子力学でも、複合システムの状態空間をそのコンポーネントのものから構築するためのルールが存在します。 という状態空間から、そのペアの状態空間(the tensorproduct of \(H_A**) and \(H_B**), written(H_A**otimes H_B**))を求めることができるルールです。 このルールには2つの重要なことがあります。1つ目は、su long as long as \(H_A) and Neither(H_B) are Hilbert spaces, will be same as well, second, there are some facts about the way (H_A \otimes H_B} relates to \(H_A) and Neither(H_B), that have surprising consequences for the relationsbetween the complex system and its parts. 特に、複合システムの状態はその構成要素の状態によって一意に定義されないことが判明した。 このことは、量子力学によれば、複合システムに関する事実(その空間的構成に関する事実だけではない)には、その構成要素に関する事実の上位に来ないものがあるということであり、全体としてのシステムに関する事実には、その部分に関する事実やそれらの部分の配置の仕方に上位に来ないものがあるということである。 この理論のこの特徴の重要性は軽視できない。この特徴は、何らかの形で、この理論の最も困難な問題のほとんどに関与している。
もう少し詳しく説明する。 \(v_{i}^A}) is an orthonormal basisfor \(H_A}) and \(u_{j}^B}) is an orthonormal basis for \(H_B}), then theset of pairs \((v_{i}^A, u_{j}^B)\) to form anorthonormal basis for the tensor product space \(H_A \otimes H_B)≒THANGLE_HIGH! また、テンソル積空間の内積は次のように定義されます。
It is a linear sum of vectors in (H_A \otimes H_Biia) although every vector in the space is itselfexible in the form (v^A \otimes u^B), and it turns out that
- any composite state defines uniquely the states of itscomponents.この構築から、全てのベクトルはこの形式で表せるものの、この形式のベクトルが全て定義されないことが判明した。
- if the states of \(A) and \(B) are pure (i.e……), corresponding byvector \(v^A) and \(u^B),respectively), then the state of \((A+B)\) is pure and represented by (v^A \otimes u^B).This is pure and representing the \((A+B)), and
- if state of \((A+B)\) is pure and expressible in form \(v^A \otimes u^B), then the states of \(A) and \(B) are pure, but
- if states of \(A) and \(B) are not pure, i.m., then the \(B) as well, but, the \(A) as well, and \(B) as well.e., の状態が純粋でない場合、つまりmixedstates(これらは以下で定義)である場合、それらはuniquelyにof \((A+B)\) を定義せず、特にform \(v^A \otimes u^B) で表現できない純粋な状態である可能性があります
2.2 Operators
演算子はベクトル空間の自分自身への写像で、ある空間内の任意のベクトル Ⓐ(\ket{B}) を同じくその空間内の別のベクトルⒷ(\ket{B’}) に取り込むものです。 線型演算子とは、以下の性質を持つ演算子です。
- Think(O(\ket{A} + \ket{B}) = O \ket{A}) + O \ket{B}), and
- (O(c \ket{A}) = c(O \ket{A})\).
Just as any vector in an \(N}-dimensional space can be represented by acolumn of \(N} numbers, relative to a choice of basis for the space, anylinear operator on the space can be represented in a column notation by a N^2) numbers.The only gonna be replaced in the space:
ヒルベルト空間とは何かという前にもう2つ定義して、量子力学に移ります。 \(O) witheigenvalue \(a) if, and only if, \(O \ket{B} = a \ket{B}).異なる演算子は異なる固有ベクトルを持つことができますが、固有ベクトルと演算子の関係は、演算子とベクトルにのみ依存し、それらが表現される特定の基底には依存しません。 エルミート演算子とは、その固有ベクトルからなる正規直交基底が存在し、それらの固有値がすべて実数であるという性質を持つ演算子である。
最後に、ヒルベルト空間とは、内積が定義され、完全である、すなわち、空間内のベクトルの任意のコーシー列が空間内のベクトルに収束するようなベクトル空間である。 有限次元の内積空間はすべて完全であり、ここではこれに限定して説明する。 無限次元の場合は、この段階では有益に入らないいくつかの複雑さを含んでいる。
量子力学
量子力学の4つの基本原理は以下の通りである。
(3.1)
物理的状態:すべての物理系はヒルベルト空間に関連付けられ、空間内のすべての単位ベクトルは系の可能な純粋状態に対応し、すべての可能な純粋状態は、空間内のいくつかのベクトルに対応します。
ハミルトニアンと呼ばれる演算子があり、これは量子論において特別な役割を担っています。 ハミルトニアンとは、系の全エネルギーを表す演算子で、”heat “と “hat “の2種類があります。 その固有値は全エネルギーを測定したときに得られる可能性のある結果です。
(3.3)
合成複雑な系のヒルベルト空間は、それを構成する単純な系(非相対論的な標準理論では個々の粒子)のテンソル積である。
(3.4) Dynamics. a.
Contexts of type 1: ある系の状態 at(t) とそれが受ける力と制約が与えられたとき、他の任意の時間における状態を与える方程式 ‘Schrödinger’sequation’ が存在する \(Uket{v_t} \rightarrow \{v_t’}}). の重要な特性は、決定論的であること、つまり、ある時点のシステムの状態を他の時点でも一意な状態にすること、ユニタリーであること、つまり、それが作用するヒルベルト空間のオートモーフィズム(すなわち。 amapping of that space onto itself that preserves the linear spacestructure and inner product), and it is linear, that if it takes a state \(\ket{A}) on the state(\ket{A’}), という状態であり、かつ、it takes the state(\ket{B’}) on the state(\alpha \{A} +beta \{B}) という形式の任意の状態をit takes the state(\alpha \{A’} + \beta ◇) on the state(\alpha ◇)。
b. タイプ2の文脈(”Measurement Contexts”):観測物質であるⒶの「測定」を行うと、その固有値に対応するⒶの固有状態に崩れ落ちる作用がある。 これはCollapsePostulateとして知られています。 このとき、どのような固有状態になるかは確率の問題であり、その確率はBornの法則と呼ばれるルールによって与えられます。
- タイプ 1 とタイプ 2 のコンテキストの区別は、量子力学用語ではまだ解明されていない。e., すなわち、システムがシュレーディンガー方程式以外の力学的規則によって支配される文脈が存在するかどうかは、解釈上未解決の問題である。
Structures on Hilbert Space
都市における場所間の関係に関するすべての情報が、それらを表す地図上の点間の空間関係によって具体化されているのと同様に、量子力学における状態および量の内部関係に関するすべての情報が、それらを表すベクトルおよび演算子の間の数学的関係によって具体化されていると私は上で言及しました。 数学的な観点から見ると、量子力学が古典的な先行研究と本当に異なるのは、状態や量がより豊かな構造を持っていることであり、それらはメンバー間の関係のより興味深いネットワークを持つファミリーを形成していることです。
量子力学系の振る舞いの物理的に重要な特徴はすべて、それらの関係の数学的性質の結果であり、その中で最も重要なものを簡単に要約すると、
(P1)
ヒルベルト空間内のベクトルの加算やスカラーによる乗算は、その空間にもあるベクトルを生み出すことになる。 そのベクトルが正規化されている場合は(3.1)からシステムの可能な状態を表し、固有値の異なる観測量(supported eigenvector of an observable \(B○○))の2つの固有値の和である場合は、それ自体は(B○○) の固有ベクトルではなく、(3.4b)から、supported a probabilities of showing one oranother result in \(B○○) measurementと関連付けられることになります。
(P2)
ヒルベルト空間上の任意のエルミート演算子について、同じ空間上に、固有ベクトルの完全なセットを共有しない他の演算子が存在する。実際、固有ベクトルを共有しない他の演算子が存在することは容易に示すことができる。 例えば、
(4.1)
Every Hermitian operator on the Hilbert spaceassociated with a system represents a distinct observable, and (hence) every normalized vector, a distinct state, and
(4.2)
A system has a value for observable \(Axx) if and only if thevector representing its state is an eigen-state of the \(Axx) opator.であると仮定している。 (P2)から(3.1)により、量子力学的状態はすべての観測値の固有状態ではないこと(実際、固有状態が共通でない観測値が存在する)、また(3.)により、その系が持つ値はちょうどその固有状態の固有値となる。2)により、量子力学系がそれに関連するすべての量に対して同時値を持つことはない(実際、どの状態も同時値を割り当てない量の組が存在する)。
There are Hermitian operators on the tensor product(H_1 \otimes H_2) of a pair of Hilbert spaces ◇(H_1) and ◇(H_2) …。 このことから、(4.1)により、(S1+S2)に係る観測値でその値が決まらない(There are observables pertaining to \((S1+S2)\))ことが分かる。
これらはすべてヒルベルト空間のベクトルと演算子をそれぞれ状態、観測値とし、Bornの法則(および後の (4.1), (4.2) )を適用して状態の割り当てに経験則を与えて得られたわかりやすい結果である。 量子力学を理解する上での真の困難は、その物理的、形而上学的、認識論的な意味合いを理解することにある。 この問題は、ヒルベルト空間の問題ではなく、力学、つまり、システムが空間を通してたどる軌跡を記述するルールの問題である。 物理学的な観点からは、これまで議論されてきたものよりもはるかに厄介な問題である。
System \(S) and a device \(S^*) that measures anobservable \(A) on \(S) with values \(a_1,a_2, a_3, …\}) があったとします。 Then there is somestate of \(S^***) (the ‘ground state’), and some observable \(B**) with values \(b_1, b_2,b_3, …).\(ポインタオブザーバブル。測定器の前面にあるダイヤルのポインタのような役割を果たすのでこう呼ばれる)を持つ観測変数があります。 と相互作用し、相互作用の直前の \(A) の値が a_1 であれば、その直後の \(B) の値は b_1 となるようなものである。 しかし、もし相互作用の直前の(A)の値が(a_2)であれば、その後の(B)の値は(b_2)、 相互作用の直前の(A)の値が(a_3)であれば、(B)の値は(b_3)、などである。 これがまさに \(S^***) measures \(A) ということです。 ということで、”the joint, partial state of \(S) and \(S^*)” (just the part of it that specifiest the value of , whose values-corresponding to joint assignments of values to the measured observable on (S) and the pointer observable on \(S^*)) by the vector (\ket{A=a_i}_s \{B=b_i}_{s^*}).と表されるとすると、このベクトルは”(S) “と” (S^) “の間にある軌跡を表しています。 を力学的記述とすると、”the \(S^****) is a measuring instrument for \(A) is that the dynamical laws entail that,
Gen
and so on…となる。
Intuitively is a measuring instrument for an observable \(A) just incase that some observable feature of \(S^*) (it doesn’t matter what, just something whose values can be ascertained by looking at thedevice), that is correlated with the \(A)-values of systems fed into it in such a way to we can read those value off of \(S^*)’s observablestate after the interaction. philosophy parlance is ameasuring instrument for \(S^***) just in case of some observablefeatures that tracks or indicate the \(A) -values of systems which which interactions in an appropriate way.
さて、上記の(3.1)から、(tomany to count) that are not eigenstates of \(A), and whatSchrödinger’s equation tells us about the joint evolution of \(S} and {tm(S^*) when \(S} is started out in one of these, if we think we the Schrödinger’s equation will us that the state of the pair after interaction are a superposition of eigenstates of .net は、相互作用後のペアの状態は(Sp*)の状態との重ね合わせであることが分かります。 このとき、on \(S) on what observable is being measuredd, and it doesn’t matter what particular superposition \(S) startsout in; when it is fed into a measurement instrument for that observable, if the interaction is correctly described by Schrödinger’sequation, that equation in the \(U), the operator that affect the transformation from the earlier to the later state of the pair, that joint state of \(S) and the apparatus after the interaction is a superposition of eigenstates of thisobservable on the joint system.とあるように、その状態から、その観測値の測定器への入力が正しく行われていれば、その方程式中のlinearityから、その観測値の固有状態の重ね合わせが得られるのです。
例えば、we start \(S^***) in its ground state, and \(S} in the state
It is the rules for obtaining the state-space of the composite system is
and it follows from fact that \(S^**) is a measuring instrument for Aœœiarchy…これは、the combined state of the pair is [複合系が合成されている状態]の取得のための規則の帰結で、”supported “は “conposite “の意味です。となり、その結合状態は
となる。 というのは、タイプ2の文脈の力学的規則(そのような文脈があるとすれば、これはその一つである)は、相互作用後のペアの状態が
または
Indeedのいずれかであることを必要とするからである。 という正確な確率と、後者になる確率が存在することを意味します。
タイプ2の文脈に対するdynamicalruleを放棄することで(あるいは同じことだが、そのような文脈があることを否定することで)論理的整合性を回復しようとできるが、その場合、経験との整合性の問題が発生する。 なぜなら、その規則が理論に含まれたのは単なる不手際ではなく、我々はシステムが与えられた観測可能性の固有状態にあるときどのように見えるかを知っており、測定後の測定装置がポインタ観測可能性の固有状態にあることを見た目で知っているのである。 5992>
これが量子力学における測定問題であり、理論の解釈、量子力学による世界のあり方、特に測定が行われている世界の断片についての詳細な物語は、この問題に取り組まなければならない。
Loose Ends
混合状態は純粋状態の加重和であり、異なる純粋状態を構成要素とするアンサンブルの状態や、部分的な知識しかない個々のシステムの状態を表すのに使用されることがある。 最初のケースでは、与えられた純粋状態に付けられた重みは、その状態にあるアンサンブルの構成要素の大きさ(したがって、アンサンブルの任意のメンバーがそうであるという客観的確率)を反映している。2番目のケースでは、状態が割り当てられた問題のシステムがその状態にあるという認識的確率を反映します。
純粋状態と混合状態の区別を失いたくないのであれば、純粋状態の集合の加重和(等価的に、それらに関連する確率関数)を表現する方法が必要であり、それは混合状態を表現する代替方法か、純粋状態と混合状態の区別を維持する統一的な表現方法のいずれかが必要なことを意味します。ヒルベルト空間には密度演算子と呼ばれる演算子があり、この演算子は後者に適しており、これまで状態ベクトルについて述べてきたことをすべて密度演算子という言葉で言い直すことは難しいことではありません。 つまり、純粋な状態がベクトルで表現されるかのように言われることがありますが、量子力学では純粋な状態も混合した状態も、密度演算子で表現されるというのが公式のルールです。
混合状態は、私が言ったように、実際には1つまたは別の純粋な状態にあるシステムの状態に対する我々の無知を表すために使用することができ、これは古典的な文脈で混合物を解釈するための適切な方法であると多くの人に思われてきたが、それを量子力学の混合物に一般的に適用するには深刻な障害がある。 これらは、この百科事典の量子力学の他の項目で詳しく説明します。
これまで観測値について述べてきたことは、厳密に言えば、観測値の値が離散集合を形成する場合にのみ適用されるもので、連続観測値の場合にこれを一般化するために必要な数学的巧妙さは複雑で、より技術的な問題を提起します。 5992>
これで、量子力学の哲学的議論に取り組むための最初の準備はすべて整ったはずですが、これは最初の一歩にすぎません。 ヒルベルト空間におけるベクトルと作用素の関係、単純な系の空間と複雑な系の空間の関係、そして状態ベクトルの空間内での移動を記述する方程式について学べば学ぶほど、この理論に関連する問題の性質と難しさの両方を理解することができるようになるのです。 量子力学の面白いところは、哲学者が限りなく夢中になれるところですが、学べば学ぶほど、問題が難しくなっていくところです
。