Kvantová mechanika
Terminologie
Fyzikální systémy se dělí na typy podle svých neměnných (neboli „stavově nezávislých“) vlastností a stav systému v daném čase se skládá z úplné specifikace těch jeho vlastností, které se s časem mění (jeho „stavově závislé“ vlastnosti). Chceme-li tedy podat úplný popis systému, musíme říci, o jaký typ systému se jedná a jaký je jeho stav v každém okamžiku jeho historie.
Fyzikální veličina je vzájemně se vylučující a společně vyčerpávající rodina fyzikálních vlastností (pro ty, kteří znají tento způsob mluvení, je to rodina vlastností se strukturou buněk v oddíle). Znalost toho, jaké druhy hodnot veličina nabývá, nám může hodně napovědět o vztazích mezi vlastnostmi, z nichž se skládá. Hodnoty bivalentní veličiny například tvoří množinu se dvěma členy; hodnoty reálně vyjádřených veličin tvoří množinu se strukturou reálných čísel. To je zvláštní případ něčeho, s čím se budeme setkávat opakovaně, totiž..,že když víme, jaké matematické objekty představují prvky v nějaké množině (zde hodnoty fyzikální veličiny; později stavy, které může systém nabývat, nebo veličiny, které se k němu vztahují), řekne nám to velmi mnoho (ba dokonce pravděpodobně vše, co je třeba vědět) o vztazích mezi nimi.
V kvantově mechanických souvislostech se termín „pozorovatelná veličina“ používá zaměnitelně s termínem „fyzikální veličina“ a měl by se považovat za technický termín se stejným významem. Není náhodou, že první tvůrci teorie zvolili tento termín, ale volba byla učiněna z důvodů, které dnes nejsou obecně přijímány. Stavový prostor systému je prostor tvořený množinou jeho možných stavů, tj. fyzikálně možných způsobů kombinace hodnot veličin, které jej vnitřně charakterizují. V klasických teoriích se množina veličin, která tvoří supervenienční základnu pro ostatní, obvykle označuje jako „základní“ nebo „fundamentální“, a protože každý matematicky možný způsob kombinace jejich hodnot je fyzikálně možný, lze stavový prostor získat tak, že je jednoduše vezmeme za souřadnice. Tak například stavový prostor klasického mechanického systému složeného z \(n\) částic, získaný zadáním hodnot\(6n\) reálně vyjádřených veličin – tří složek polohy a tří složek hybnosti pro každou částici v systému – je\(6n\) rozměrný souřadnicový prostor. Každý možný stav takového systému odpovídá bodu v prostoru a každý bod v prostoru odpovídá možnému stavu takového systému. Trochu jiná situace je v kvantové mechanice, kde existují matematicky popsatelné způsoby kombinování hodnot veličin, které nepředstavují fyzikálně možné stavy. Jak uvidíme, stavové prostory kvantové mechaniky jsou speciálními druhy vektorových prostorů, známých jako Hilbertovy prostory, a mají větší vnitřní strukturunež jejich klasické protějšky.
Struktura je množina prvků, na které jsou definovány určitéoperace a vztahy, matematickástruktura je právě struktura, ve které jsou prvkymatematické objekty (čísla, množiny, vektory) a operacematematické, a model je matematickástruktura používaná k reprezentaci nějaké fyzikálně významné strukturyve světě.
Srdce a duše kvantové mechaniky je obsaženo v Hilbertově prostoru, který reprezentuje stavové prostory kvantově mechanických systémů. vnitřní vztahy mezi stavy a veličinami a vše, co z toho vyplývá o způsobech chování kvantově mechanických systémů, jsou vetkány do struktury těchto prostorů, ztělesněny ve vztazích mezi matematickými objekty, které je reprezentují. To znamená, že pochopení toho, jak se systém podle kvantové mechaniky chová, je neoddělitelné od znalosti vnitřní struktury těchto prostorů. Znáte-li Hilbertův prostor a seznámíte-li se s dynamickými zákony, které popisují dráhy, jimiž se vektory v něm pohybují, víte o systémech, které popisuje, vše, co je třeba vědět, v termínech stanovených teorií.
Pod pojmem „znát Hilbertův prostor“ mám na mysli něco víc než vlastnit jeho popis nebo mapu; to má každý, kdo má na poličce učebnici kvantové mechaniky. Myslím tím, že se v něm vyznáte tak, jako se vyznáte ve městě, ve kterém žijete. Jedná se o praktický druh znalostí, které přicházejí postupně a nejlépe se získávají tím, že se učíte řešit problémy této formy: Jak se dostanu z bodu A do bodu B? Mohu se tam dostat, aniž bych musel projítC? A jaká je nejkratší cesta? Postgraduální studenti fyziky tráví dlouhá léta tím, že se seznamují se zákoutími hilberského prostoru, vyhledávají známé orientační body, prošlapávají vyšlapané cestičky, učí se, kde leží tajné chodby a slepé uličky, a rozvíjejí si smysl pro celkovou orientaci v terénu. Učí se orientovat v Hilbertově prostoru způsobem, jakým se taxikář učí orientovat ve svém městě.
Kolik takových znalostí je zapotřebí k tomu, aby bylo možné přistoupit k filozofickým problémům spojeným s teorií? Na začátku ne příliš mnoho: jen nejobecnější fakta o geometrii krajiny (která je v každém případě, na rozdíl od většiny měst, krásně uspořádaná) a o cestách, které (vektory reprezentující stavy) systémů procházejí. To je to, co zde bude představeno: nejprve trocha jednoduché matematiky a pak v kostce teorie.
Matematika
2.1 Vektory a vektorové prostory
Vektor \(A\), psáno „\(\ket{A}\)“, je matematický objekt charakterizovaný délkou, \(|A|\), a směrem. Anormalizovaný vektor je vektor délky 1, tj. \(|A| = 1\). Vektory lze sčítat, násobit konstantami (včetně komplexních čísel) a násobit. Sčítání vektorů mapuje libovolnou dvojici vektorů na jiný vektor, konkrétně takový, který získáte posunutím druhého vektoru tak, aby se jeho ocas shodoval s vrcholem prvního, aniž by se změnila délka nebo směr obou vektorů, a následným připojením ocasu prvního vektoru k vrcholu druhého. Toto pravidlo sčítání je známé jako zákon rovnoběžníku. Tak například sčítáním vektorů \(\ket{A}\) a \(\ket{B}}) získáme vektor \(\ket{C}). (= \ket{A} + \ket{B})\) podle obrázku 1:
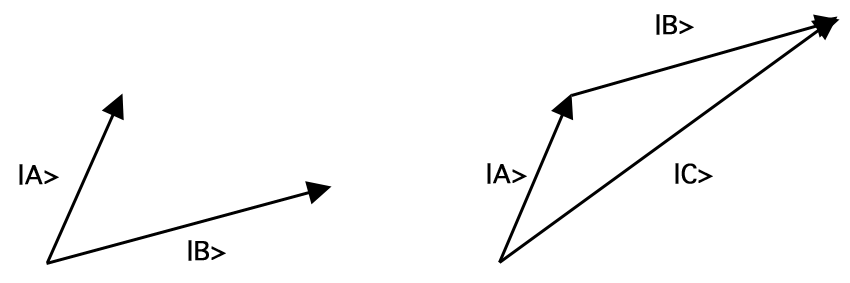
Obrázek 1.Sčítání vektorů
Sčítáním vektoru \(\ket{A}\) s \(n\), kde \(n\) je konstanta, získáme vektor, který má stejný směr jako \(\ket{A}\), ale jehož délka je \(n\) krát délka \(\ket{A}\).
V reálném vektorovém prostoru je (vnitřní nebo tečkový) součin dvojice vektorů \(\ket{A}\) a \(\ket{B}}), psáno „\(\braket{A}{B}\)“, skalár rovný součinu jejich délek (nebo „norem“) krát kosinus úhlu \(\theta\) mezi nimi:
\
Nechť \(\ket{A_1}\) a \(\ket{A_2}\) jsou vektory délky 1 („jednotkové vektory“) takové, že \(\braket{A_1}{A_2} = 0\). (Úhel mezi těmito dvěma jednotkovými vektory musí být 90 stupňů.) Pak můžeme jakýkoli dvourozměrný vektor \(\ket{B}\) znázornit pomocí našich jednotkových vektorů takto:
\
Například zde je graf, který ukazuje, jak lze \(\ket{B}\) reprezentovat jako součet dvou jednotkových vektorů \(\ket{A_1}\) a \(\ket{A_2}\):
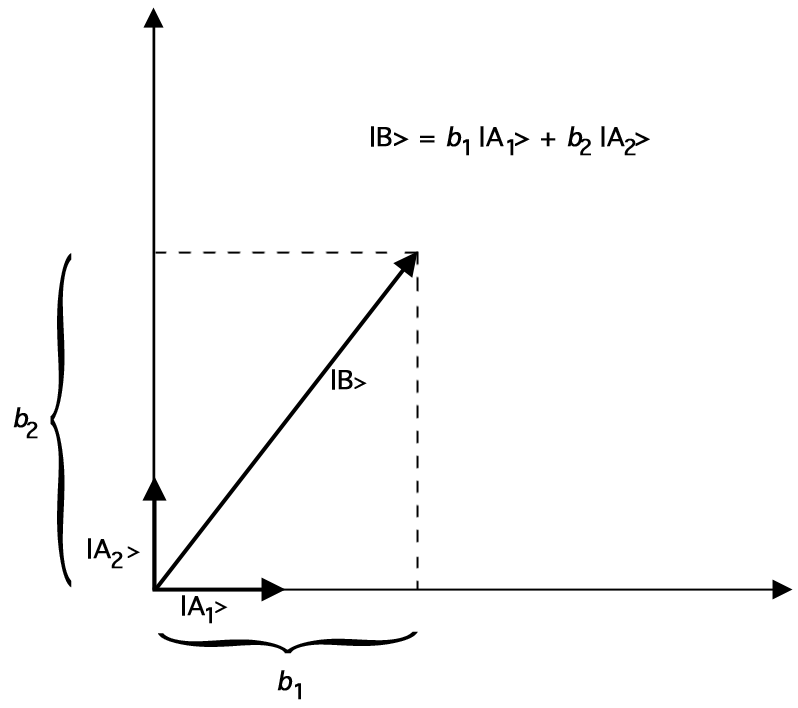
Obrázek 2. Zobrazení \(\ket{B}\) vektorovým součtem jednotkových vektorů
Nyní je třeba upravit definici vnitřního součinu \(\braket{A}{B}\) tak, aby platila pro komplexní prostory. Nechť \(c^*\) je komplexní konjugát \(c\). (Je-li \(c\) komplexní číslo tvaru \(a \pm bi\), pak je komplexní konjugát\(c^*\) \(c\) definován takto:
\^* = a-bi \\^* = a+bi\]
Takže pro všechna komplexní čísla \(c\) platí \(^* = c\),ale \(c^* = c\) jen v případě, že \(c\) je reálné.). Nyní lze definovat vnitřní součin \(\ket{A}\) a \(\ket{B}\) pro komplexní prostory pomocí konjugátů komplexních koeficientů takto. Kde \(\ket{A_1}\) a \(\ket{A_2}\) jsou dříve popsané jednotkové vektory, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}\) a \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}), pak
\
Nejobecnější a nejabstraktnější pojem vnitřního součinu, jehož dva speciální případy jsme nyní definovali, je následující. \(\braket{A}{B}\) je vnitřní součin na vektorovém prostoru \(V\) právě v případě
- \(\braket{A}{A} = |A|^2\), a \(\braket{A}{A}=0\) tehdy a jen tehdy, když \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}^*\)
- \(\braket{B}{A+C}=\braket{B}{A} + \braket{B}{C}).
Z toho vyplývá, že
- délka \(\ket{A}}\) je odmocninou vnitřního součinu \(\ket{A}}\) se sebou samým, tj,\
a
- \(\ket{A}}) a \(\ket{B}}) jsou navzájem kolmé nebo pravoúhlé tehdy a jen tehdy, když \(\braket{A}{B}).
Vektorový prostor je množina vektorů uzavřená při sčítání a násobení konstantami, vnitřní součinový prostor je vektorový prostor, na kterém byla definována operace násobení vektorů, a dimenze takového prostoru je maximální počet nenulových, vzájemně ortogonálních vektorů, které obsahuje.
Každý soubor \(N\) vzájemně ortogonálních vektorů délky 1 v\(N\)-rozměrném vektorovém prostoru představuje ortonormální základnu tohoto prostoru. Nechť \(\ket{A_1}, \ldots, \ket{A_N}\) je takový soubor jednotkových vektorů. Pak každý vektor v prostoru lze vyjádřit jako součet tvaru:
\
kde \(b_i = \braket{B}{A_i}\). Hodnoty \(b_i\) jsou zde známé jako koeficienty rozšíření \(B\) v bázi \(A\).
Všimněte si, že:
- pro všechny vektory \(A\), \(B\) a \(C\) v daném prostoru,\
- pro všechny vektory \(M\) a \(Q\), vyjádřené v termínech \(A\)-báze,\
a
\
Existuje i jiný způsob zápisu vektorů, a to zápisem koeficientůrozšíření (vzhledem k dané bázi) ve sloupci, např:
\
kde \(q_i = \braket{Q}{A_i}\) a \(A_i\) jsou vektory zvolené báze.
Když máme co do činění s vektorovými prostory nekonečné dimenze, protože nemůžeme zapsat celý sloupec expanzních koeficientů potřebných k vytipování vektoru, protože by musel být nekonečně dlouhý, tak místo toho zapíšeme funkci (nazývanou „vlnová funkce“ pro\(Q\), obvykle reprezentovanou \(\psi(i))\), která má tyto koeficienty jako hodnoty. Zapíšeme tedy funkci:
\
Při zadání libovolného vektoru a libovolné báze vektorového prostoru můžeme získat vlnovou funkci vektoru v této bázi; a při zadání vlnové funkce pro vektor v určité bázi můžeme sestrojit vektor, jehož vlnová funkce to je. Protože se ukazuje, že většina důležitých operací s vektory odpovídá jednoduchým algebraickým operacím s jejich vlnovými funkcemi, je to obvyklý způsob reprezentace stavových vektorů.
Když dvojice fyzikálních systémů interaguje, tvoří složený systém a v kvantové mechanice, stejně jako v klasické mechanice, existuje pravidlo pro konstrukci stavového prostoru složeného systému z prostorů jeho složek, pravidlo, které nám říká, jak ze stavových prostorů \(H_A\) a \(H_B\) pro \(A\) a \(B\) získat stavový prostor – nazývaný „tenzorový součin“ \(H_A\) a \(H_B\) a zapsaný\(H_A \krát H_B\) – této dvojice. Na tomto pravidle jsou důležité dvě věci: zaprvé, dokud jsou \(H_A\) a\(H_B\) Hilbertovými prostory, bude jimi i \(H_A \otimes H_B\), a zadruhé, existují některé skutečnosti o tom, jak se \(H_A \otimes H_B\) vztahuje k \(H_A\) a\(H_B\), které mají překvapivé důsledky pro vztahy mezi komplexním systémem a jeho částmi. Zejména se ukazuje, že stav složeného systému není jednoznačně definován stavem jeho složek. To znamená, nebo se to tak alespoň jeví, že podle kvantové mechaniky existují fakta o složených systémech (a nejen fakta o jejich prostorové konfiguraci), která nejsou nadřazena faktům o jejich součástech; to znamená, že existují fakta o systémech jako celcích, která nejsou nadřazena faktům o jejich částech a způsobu, jakým jsou tyto části uspořádány. Význam tohoto rysu teorie nelze bagatelizovat; tak či onak se podílí na většině jejích nejobtížnějších problémů.
Trochu podrobněji: Pokud je \(\{v_{i}^A\}\) ortonormální bází pro \(H_A\) a \(\{u_{j}^B\}\) je ortonormální bází pro \(H_B\), pak množina dvojic \((v_{i}^A, u_{j}^B)\) tvoří ortonormální bázi pro prostor tenzorového součinu \(H_A \otimes H_B\). Označení \(v_i^A \otimes u_j^B\) se používá pro dvojici \((v_{i}^A,u_{j}^B)\) a vnitřní součin na \(H_A \otimes H_B\) je definován jako:
\
Výsledkem této konstrukce je, že ačkoli každý vektor v\(H_A \otimes H_B\) je lineárním součtem vektorů vyjádřitelných ve tvaru\(v^A \otimes u^B\), ne každý vektor v prostoru je vyjádřitelný v tomto tvaru a ukazuje se, že
- každý složený stav jednoznačně definuje stavy svých složek.
- Jestliže jsou stavy \(A\) a \(B\) čisté (tj, reprezentovatelné vektory \(v^A\) a \(u^B\), v tomto pořadí), pak stav \((A+B)\) je čistý a reprezentovaný vektorem \(v^A \otimes u^B\), a
- pokud je stav \((A+B)\) čistý a vyjádřitelný ve tvaru \(v^A \otimes u^B\), pak jsou stavy \(A\) a \(B\) čisté, ale
- pokud stavy \(A\) a \(B\) čisté nejsou, tj.e., jsou-li to smíšené stavy (ty jsou definovány níže), nedefinují jednoznačně stav \((A+B)\); zejména může jít o čistý stav, který není vyjádřitelný ve tvaru \(v^A \otimes u^B\).
2.2 Operátory
Operátor \(O\) je mapování vektorového prostoru na sebe sama; přenáší libovolný vektor \(\ket{B}\) v prostoru na jiný vektor \(\ket{B‘}\) rovněž v prostoru; \(O \ket{B} = \ket{B‘}\). Lineární operátory jsou operátory, které mají následující vlastnosti:
- \(O(\ket{A} + \ket{B}) = O \ket{A}.
- \(O(c \ket{A}) = c(O \ket{A})\).
Stejně jako lze jakýkoli vektor v \(N\)-rozměrném prostoru reprezentovat sloupcem \(N\) čísel, vzhledem k volbě báze prostoru, lze jakýkoli lineární operátor v prostoru reprezentovat ve sloupcovém zápisu pomocí\(N^2\) čísel:
\
kde \(O_{ij} = \braket{A_i}{O \mid A_j}\) a \(A_N\) jsou bázové vektory prostoru. Vliv lineárního operátoru \(O\) na vektor\(B\) je pak dán vztahem
\
Dvě další definice, než budeme moci říci, co jsou Hilbertovy prostory, a pak se můžeme věnovat kvantové mechanice. \(\ket{B}\) je vlastním vektorem \(O\) s vlastní hodnotou \(a\) tehdy a jen tehdy, když \(O \ket{B} = a \ket{B}\).Různé operátory mohou mít různé vlastní vektory, ale vztah vlastního vektoru a operátoru závisí pouze na daném operátoru a vektorech, nikoli na konkrétní bázi, ve které jsou vyjádřeny; vztah vlastního vektoru a operátoru je, to znamená, invariantní při změně báze. Hermitovský operátor je operátor, který má tu vlastnost, že existuje ortonormální báze složená z jeho vlastních vektorů a že tato vlastní čísla jsou všechna reálná.
Hilbertův prostor je konečně vektorový prostor, na kterém je definován vnitřní součin a který je úplný, tj. který je takový, že každá Cauchyho posloupnost vektorů v prostoru konverguje k vektoru v prostoru. Všechny konečněrozměrné prostory vnitřního součinu jsouúplné a já se na ně omezím. Nekonečný případobsahuje některé komplikace, do kterých není v této fázi účelné vstupovat.
Kvantová mechanika
Čtyři základní principy kvantové mechaniky jsou:
(3.1)
Fyzikální stavy.Každý fyzikální systém je spojen s Hilbertovým prostorem, každý jednotkový vektor v prostoru odpovídá možnému čistému stavu systému a každý možný čistý stav nějakému vektoru v prostoru.
(3.2)
Fyzikální veličiny.Hermitovské operátory v Hilbertově prostoru spojené se systémemreprezentují fyzikální veličiny a jejich vlastní hodnoty představujímožné výsledky měření těchto veličin.
Existuje operátor, nazývaný Hamiltonián, který hraje v kvantové teorii zvláštní roli, protože dynamiku systému lze pohodlně formulovat sledováním jeho vývoje. Hamiltonián – psáno \(H\) nebo \(\hat{H}\) – znamená celkovou energii systému. Jeho vlastní hodnoty jsou možné výsledky, které lze získat při měření celkové energie. Je dána součtem kinetických a potenciálních energií složek systému.
(3.3)
Kompozice.Hilbertův prostor spojený s komplexním systémem je tenzorovým součinem prostorů spojených s jednoduchými systémy (ve standardní, nerelativistické teorii: jednotlivými částicemi), z nichž se skládá.
(3.4) Dynamika. a.
Souvislosti typu 1: Vzhledem ke stavu systému v čase \(t\) a silám a omezením, kterým podléhá, existuje rovnice, „Schrödingerova sekvence“, která udává stav v libovolném jiném čase \(U\ket{v_t} \rightarrow \ket{v_{t‘}}\). Důležité vlastnosti \(U\) pro naše účely jsou, že je deterministická, což znamená, že přenáší stav systému v jednom čase do jednoznačného stavu v každém jiném čase, je unitární, což znamená, že je automorfismem Hilbertova prostoru, na kterém působí (tj, je to přenesení tohoto prostoru na sebe sama, které zachovává lineární prostorovou strukturu a vnitřní součin), a je lineární, což znamená, že pokud přenáší stav \(\ket{A}\) na stav\(\ket{A‘}\), a bere stav \(\ket{B}\) na stav \(\ket{B‘}\), pak bere jakýkoli stav tvaru \(\alfa \ket{A} + \beta \ket{B}\) na stav \(\alfa \ket{A‘} + \beta \ket{B‘}\).
b.
Kontexty typu 2 („kontexty měření“): Provedení „měření“ pozorovatelné veličiny \(B\) na systému ve stavu \(\ket{A}\) má za následek zhroucení systému do vlastního stavu \(B\), který odpovídá pozorované vlastní hodnotě. Tomuto jevu se říká kolapsový postulát. Do kterého konkrétního \(B\)-vlastního stavu se systém zhroutí, je otázkou pravděpodobnosti a pravděpodobnost je dána pravidlem známým jako Bornovo pravidlo:
\
U těchto dvou druhů souvislostí je třeba si povšimnout dvou důležitých bodů:
- Rozlišení mezi kontexty typu 1 a 2 zůstává v kvantově mechanických termínech nevyjasněno; nikomu se nepodařilo zcela uspokojivě říci, v termínech stanovených teorií, které kontexty jsou kontexty měření, a
- I když je rozlišení vyjasněno, je otevřenou interpretační otázkou, zda existují kontexty typu 2; tj.e., je otevřenou interpretační otázkou, zda existují kontexty, v nichž se systémy řídí jiným dynamickým pravidlem než Schrödingerovou rovnicí.
Struktury na Hilbertově prostoru
Výše jsem poznamenal, že stejně jako jsou všechny informace, které máme o vztazích mezi místy ve městě, obsaženy v prostorových vztazích mezi body na mapě, které je reprezentují, jsou všechny informace, které máme o vnitřních vztazích mezi stavy a veličinami v kvantové mechanice (a mezi nimi), obsaženy v matematických vztazích mezi vektory a operátory, které je reprezentují. Z matematického hlediska se kvantová mechanika od svých klasických předchůdců liší tím, že stavy a veličiny mají bohatší strukturu; tvoří rodiny se zajímavější sítí vztahů mezi jejich členy.
Všechny fyzikálně důsledné vlastnosti chování kvantově mechanických systémů jsou důsledky matematických vlastností těchto vztahů a nejdůležitější z nich lze snadno shrnout:
(P1)
Každý způsob sčítání vektorů v Hilbertově prostoru nebo jejich násobení skaláry dá vektor, který je také v tomto prostoru. V případě, že je vektor normalizovaný, bude z (3.1) představovat možný stav systému a v případě, že je součtem dvojice vlastních vektorů pozorovatelné veličiny \(B\) s různými vlastními hodnotami, nebude sám o sobě vlastním vektorem \(B\), ale bude z (3.4b) spojen se souborem pravděpodobností, že se při měření \(B\) projeví ten či onen výsledek.
(P2)
Pro každý hermitovský operátor na Hilbertově prostoru existují na stejném prostoru jiné, s nimiž nesdílí úplnou množinu vlastních vektorů; je totiž snadné ukázat, že existují jiné takové operátory, s nimiž nemá žádné vlastní vektory společné.
Přijmeme-li několik dalších interpretačních předpokladů, můžeme říci více. Předpokládejme například, že
(4.1)
Každý hermitovský operátor na Hilbertově prostoruasociovaný se systémem reprezentuje určitou pozorovatelnou veličinu a (tedy)každý normalizovaný vektor určitý stav a
(4.2)
Systém má hodnotu pozorovatelné veličiny \(A\) tehdy a jen tehdy, když vektor reprezentující jeho stav je vlastním vektorem operátoru \(A\)-. Hodnota, kterou má, je v takovém případě právě vlastní hodnota spojená s tímto vlastním stavem.
Z (P2) vyplývá podle (3.1), že žádný kvantově mechanický stav není vlastním stavem všech pozorovatelných veličin (a že skutečně existují pozorovatelné veličiny, které nemají žádné společné vlastní stavy), a tak podle (3.2) platí, že žádný kvantově mechanický stav není vlastním stavem všech pozorovatelných veličin.2), že žádný kvantově mechanický systém nikdy nemá současné hodnoty všech veličin, které se k němu vztahují (a že skutečně existují dvojice veličin, kterým žádný stav nepřiřazuje současné hodnoty).
Existují hermitovské operátory na tenzorovém součinu\(H_1 \otimes H_2\) dvojice Hilbertových prostorů\(H_1\) a \(H_2\) … V případě, že \(H_1\) a\(H_2\) jsou stavové prostory systémů \(S1\) a \(S2\),\(H_1 \otimes H_2\) je stavový prostor komplexního systému \((S1+S2)\). Z toho podle (4.1) vyplývá, že existují pozorovatelné veličiny vztahující se k \((S1+S2)\), jejichž hodnoty nejsou určeny hodnotami pozorovatelných veličin vztahujících se k oběma jednotlivě.
To vše jsou přímé důsledky toho, že vektory a operátory v Hilbertově prostoru reprezentují stavy a pozorovatelné veličiny a že se použije Bornovo pravidlo (a později (4.1) a (4.2)), aby se přiřazením stavů dal empirický význam. To vše je dokonale pochopeno; skutečný problém v pochopení kvantové mechaniky spočívá ve vypořádání se s jejich důsledky – fyzikálními, metafyzickými a epistemologickými.
Každý, kdo se snaží dospět k pochopení toho, co kvantová mechanika říká o světě, se musí vypořádat s jednou zbývající skutečností. Tentoproblém se netýká Hilbertových prostorů, ale dynamiky – pravidel, která popisují trajektorie, jimiž systémy procházejí prostorem. Z fyzikálního hlediska je to mnohem nebezpečnější než cokoli, o čem se doposud hovořilo. Nejenže představuje obtíže pro někoho, kdo se snaží poskytnout interpretaci teorie, ale také se zdá, že ukazuje na logickou nekonzistenci v základech teorie.
Předpokládejme, že máme systém \(S\) a zařízení \(S^*\), které měří pozorovanou veličinu \(A\) na \(S\) s hodnotami \(\{a_1,a_2, a_3, …\}\). Pak existuje nějaký stav \(S^*\) („základní stav“) a nějaká pozorovatelná veličina \(B\) s hodnotami \(\{b_1, b_2,b_3, …).\}\) vztahující se k \(S^*\) (jeho „pozorovatelný ukazatel“, nazývaný tak proto, že hraje roli ukazatele na číselníku na přední straně schematického měřicího přístroje při registraci výsledku experimentu), které jsou takové, že pokud je \(S^*\) spuštěn v základním stavu a vhodným způsobem interaguje s \(S\) a pokud hodnota \(A\) bezprostředně před interakcí je\(a_1\), pak hodnota \(B\) bezprostředně poté je\(b_1\). Je-li však hodnota \(A\) bezprostředně před interakcí \(a_2\), pak hodnota \(B\) po ní je \(b_2\); je-li hodnota \(A\) bezprostředně před interakcí \(a_3\), pak hodnota \(B\) bezprostředně po ní je \(b_3\) atd. Právě to znamená, že \(S^*\) měří \(A\). Pokud tedy znázorníme společný, částečný stav \(S\) a \(S^*\) (jen tu jeho část, která určuje hodnotu , pozorovatelné, jejíž hodnoty odpovídají společnému přiřazení hodnot měřené pozorovatelné na \(S\) a ukazující pozorovatelné na \(S^*\)) vektorem \(\ket{A=a_i}_s \ket{B=b_i}_{s^*}\), a nechť „\(\rightarrow\)“ znamená dynamický popis interakce mezi nimi, říci, že \(S^*\) je měřicím přístrojem pro \(A\), znamená říci, že dynamické zákony znamenají, že,
\
a tak dále.
Intuitivně je \(S^*\) měřicím přístrojem pro pozorovatelné \(A\) jen v případě, že existuje nějaká pozorovatelná vlastnost \(S^*\) (nezáleží na tom jaká, jen něco, co lze zjistit pohledem na přístroj), která koreluje s hodnotami \(A\) systémů, které jsou do něj přiváděny tak, že tyto hodnoty můžeme odečíst z pozorovatelného stavu \(S^*\) po interakci. Ve filosofické řeči je \(S^*\) měřícím nástrojem pro \(A\) v případě, že existuje nějaká pozorovatelná vlastnost \(S^*\), která sleduje nebo indikuje hodnoty \(A\) systémů, s nimiž vhodným způsobem interaguje.
Nyní z výše uvedeného (3.1) vyplývá, že existují stavy \(S\) (je jich příliš mnoho na to, abychom je spočítali), které nejsou vlastními stavy \(A\), a pokud uvážíme, co nám říká Schrödingerova rovnice o společném vývoji \(S\) a \(S^*\), když \(S\) začíná v jednom z nich, zjistíme, že stav dvojice po interakci je superpozicí vlastních stavů . Nezáleží na tom, jaká pozorovatelná veličina na \(S\) je měřena, a nezáleží na tom, v jaké konkrétní superpozici \(S\) začíná; pokud je interakce správně popsána Schrödingerovou sekvencí, vyplývá z linearity \(U\) v této rovnici, operátoru, který provádí transformaci z dřívějšího do pozdějšího stavu dvojice, že společný stav \(S\) a přístroje po interakci je superpozicí vlastních stavů této pozorovatelné ve společném systému.
Předpokládejme například, že začínáme \(S^*\) v základním stavu a \(S\) ve stavu
\
Z pravidel pro získání stavového prostoru složené soustavy vyplývá, že kombinovaný stav dvojice je
\
a vyplývá z toho, že \(S^*\) je měřicím přístrojem pro \(A\),a linearity \(U\), že jejich kombinovaný stav po interakci je
\
To však, je v rozporu s dynamickým pravidlem pro kontexty typu 2, neboť dynamické pravidlo pro kontexty typu 2 (a pokud existují nějaké takové kontexty, pak je to tento) znamená, že stav dvojice po interakci je buď
\
nebo
\
Indeed, znamená, že existuje přesná pravděpodobnost \(\frac{1}{2}\), že skončí v prvním případě, a pravděpodobnost \(\frac{1}{2}\), že skončí v druhém případě.
Můžeme se pokusit obnovit logickou konzistenci tím, že se vzdáme dynamického pravidla pro kontexty typu 2 (nebo, což je totéž, popřeme, že nějaké takové kontexty existují), ale pak máme problém konzistence se zkušeností. Nebylo totiž pouhou chybou, že toto pravidlo bylo do teorie zahrnuto; víme, jak systém vypadá, když je v eigenstatech dané pozorovatelné veličiny, a od pohledu víme, že měřicí aparatura po měření je v eigenstatech ukazované pozorovatelné veličiny. A tak od počátku víme, že pokud nám teorie říká něco jiného o stavech měřicích aparátů po měření, ať už je to cokoli jiného, je to špatně.
To je v kostce problém měření v kvantové mechanice; jakákoli interpretace teorie, jakýkoli podrobný příběh o tom, jak vypadá svět podle kvantové mechaniky, a zejména ty části světa, ve kterých probíhá měření, se s ním musí vypořádat.
Volné konce
Smíšené stavy jsou vážené součty čistých stavů a lze je použít k reprezentaci stavů souborů, jejichž složky jsou v různých čistých stavech, nebo stavů jednotlivých systémů, o nichž máme jen částečné znalosti. V prvním případě váha přiřazená danému čistému stavu odráží velikost složky souboru, která se v tomto stavu nachází (a tedy objektivní pravděpodobnost, že se v něm nachází libovolný člen souboru); v druhém případě odráží epistemickou pravděpodobnost, že se v tomto stavu nachází dotazovaný systém, kterému je stav přiřazen.
Pokud nechceme ztratit rozdíl mezi čistými a smíšenými stavy, potřebujeme způsob reprezentace váženého součtu souboru čistých stavů (ekvivalentně pravděpodobnostních funkcí s nimi spojených), který se liší od sčítání (vhodně vážených) vektorů, které je reprezentují, a to znamená, že potřebujeme buď alternativní způsob reprezentace smíšených stavů, nebo jednotný způsob reprezentace čistých i smíšených stavů, který zachová rozdíl mezi nimi.V Hilbertových prostorech existuje druh operátoru, který se nazývá operátor hustoty, který dobře slouží v této druhé funkci, a ukazuje se, že není těžké přeformulovat vše, co bylo řečeno o stavových vektorech, v termínech operátorů hustoty. Ačkoli se tedy běžně hovoří o tom, že čisté stavy jsou reprezentovány vektory, oficiálním pravidlem je, že stavy – jak čisté, tak smíšené – jsou v kvantové mechanice reprezentovány operátory hustoty.
Ačkoli smíšené stavy mohou být, jak jsem řekl, použity k vyjádření naší neznalosti stavů systémů, které jsou ve skutečnosti v jednom nebo druhém čistém stavu, a ačkoli se to mnohým zdálo jako vhodný způsob interpretace směsí v klasickém kontextu, existují vážné překážky pro jeho obecné použití na kvantově mechanické směsi. Ty jsou ponechány na podrobnou diskusi v jiných heslech o kvantové mechanice v Encyklopedii.
Vše, co bylo řečeno o pozorovatelných veličinách, se přísně vzato vztahuje pouze na případ, kdy hodnoty pozorovatelné veličiny tvoří diskrétní množinu; matematické jemnosti, které jsou potřebné k zobecnění na případ spojitých pozorovatelných veličin, jsou komplikované a vyvolávají problémy spíše technické povahy. I ty je nejlépe ponechat na podrobnou diskusi.
Toto by měla být veškerá počáteční příprava, kterou člověk potřebuje, aby mohl přistoupit k filozofické diskusi o kvantové mechanice, ale je to jen první krok. Čím více se člověk dozví o vztazích mezi vektory a operátory v Hilbertově prostoru a mezi nimi, o tom, jak souvisí prostory jednoduchých systémů s prostory složitých systémů, a o rovnici, která popisuje, jak se stavové vektory pohybují v prostoru, tím lépe pochopí povahu i obtížnost problémů spojených s touto teorií. Legrační na kvantové mechanice je to, že čím více se člověk učí, tím jsou problémy těžší.