Mécanique quantique
Terminologie
Les systèmes physiques sont divisés en types selon leurs propriétés immuables (ou « indépendantes de l’état »), et l’état d’un système à un moment donné consiste en une spécification complète de celles de ses propriétés qui changent avec le temps (ses propriétés « dépendantes de l’état »). Pour donner une description complète d’un système, il faut donc dire de quel type de système il s’agit et quel est son état à chaque moment de son histoire.
Une quantité physique est une famille mutuellement exclusive et conjointement exhaustive de propriétés physiques (pour ceux qui connaissent cette façon de parler, c’est une famille de propriétés ayant la structure des cellules d’une partition). Le fait de connaître les types de valeurs d’une quantité peut nous en apprendre beaucoup sur les relations entre les propriétés qui la composent. Les valeurs d’une quantité bivalente, par exemple, forment un ensemble à deux membres ; les valeurs d’une quantité à valeurs réelles forment un ensemble ayant la structure des nombres réels. Il s’agit d’un cas particulier d’une chose que nous verrons encore et encore, à savoir..,que le fait de savoir quel type d’objets mathématiques représente les éléments d’un certain ensemble (ici, les valeurs d’une quantité physique ; plus tard, les états qu’un système peut prendre, ou les quantités qui s’y rapportent) nous en dit très long (en fait, on peut soutenir que c’est tout ce qu’il y a à savoir) sur les relations entre eux.
Dans les contextes de la mécanique quantique, le terme « observable » est utilisé de manière interchangeable avec « quantité physique », et devrait être traité comme un terme technique ayant la même signification. Ce n’est pas un hasard si les premiers développeurs de la théorie ont choisi ce terme, mais ce choix a été fait pour des raisons qui ne sont pas, de nos jours, généralement acceptées. L’espace d’état d’un système est l’espace formé par l’ensemble de ses états possibles, c’est-à-dire les manières physiquement possibles de combiner les valeurs des quantités qui le caractérisent intérieurement. Dans les théories classiques, un ensemble de quantités qui forme une base de supervision pour le reste est généralement désigné comme « de base » ou « fondamental » et, puisque toute façon mathématiquement possible de combiner leurs valeurs est une possibilité physique, l’espace d’état peut être obtenu en prenant simplement ces quantités comme coordonnées. Ainsi, par exemple, l’espace d’état d’un système mécanique classique composé de \(n\) particules, obtenu en spécifiant les valeurs de \(6n\) quantités à valeurs réelles – trois composantes de position, et trois de quantité de mouvement pour chaque particule du système – est un espace de coordonnées à \(6n\) dimensions. Chaque état possible d’un tel système correspond à un point de cet espace, et chaque point de cet espace correspond à un état possible d’un tel système. La situation est un peu différente en mécanique quantique, où il existe des moyens mathématiquement descriptibles de combiner les valeurs des quantités qui ne représentent pas des états physiquement possibles. Comme nous le verrons, les espaces d’état de la mécanique quantique sont des types spéciaux d’espaces vectoriels, connus sous le nom d’espaces de Hilbert, et ils ont plus de structure interne que leurs homologues classiques.
Une structure est un ensemble d’éléments sur lesquels certaines opérations et relations sont définies, une structure mathématique est juste une structure dans laquelle les éléments sont des objets mathématiques (nombres, ensembles, vecteurs) et les opérations des objets mathématiques, et un modèle est une structure mathématique utilisée pour représenter une certaine structure physiquement significative dans le monde.
Le cœur et l’âme de la mécanique quantique sont contenus dans les espaces de Hilberts qui représentent les espaces d’état des systèmes mécaniques quantiques.Les relations internes entre les états et les quantités, et tout ce que cela implique sur la façon dont les systèmes mécaniques quantiques se comportent, sont tous tissés dans la structure de ces espaces, incarnés dans les relations entre les objets mathématiques qui les représentent. Cela signifie que la compréhension du comportement d’un système selon la mécanique quantique est inséparable de la connaissance de la structure interne de ces espaces. Connaissez votre chemin autour de l’espace de Hilbert, et devenez familier avec les lois dynamiques qui décrivent les chemins que les vecteurs parcourent à travers lui, et vous savez tout ce qu’il y a à savoir, dans les termes fournis par la théorie, sur les systèmes qu’elle décrit.
Par « connaître votre chemin autour » de l’espace de Hilbert, je veux dire quelque chose de plus que posséder une description ou une carte de celui-ci ; toute personne qui a un manuel de mécanique quantique sur son étagère a cela. Je veux dire qu’il faut s’y retrouver, comme on se retrouve dans la ville où l’on vit. Il s’agit d’un type de connaissance pratique qui s’acquiert progressivement et qui s’acquiert le mieux en apprenant à résoudre des problèmes de ce type : Comment puis-je aller de A à B ? Puis-je y arriver sans passer par C ? Et quel est le chemin le plus court ? Les étudiants diplômés en physique passent de longues années à se familiariser avec les coins et recoins de l’espace de Hilbert, à repérer les points de repère familiers, à emprunter les sentiers battus, à apprendre où se trouvent les passages secrets et les impasses, et à développer un sens de la configuration générale du terrain. Ils apprennent à naviguer dans l’espace de Hilbert de la même manière qu’un chauffeur de taxi apprend à naviguer dans sa ville.
Quelle quantité de ce type de connaissances est nécessaire pour aborder les problèmes philosophiques associés à la théorie ? Au début, pas grand chose : juste les faits les plus généraux sur la géométrie du paysage terrestre (qui est, de toute façon, contrairement à celui de la plupart des villes, magnifiquement organisé), et les chemins que (les vecteurs représentant les états des) systèmes parcourent à travers eux. C’est ce qui seraintroduit ici : d’abord un peu de mathématiques faciles, puis, en résumé, la théorie.
Mathématiques
2.1 Vecteurs et espaces vectoriels
Un vecteur \(A\), écrit ‘\(\ket{A}\)’, est un objet mathématique caractérisé par une longueur, \(|A|\), et une direction. Un vecteur normalisé est un vecteur de longueur 1, c’est-à-dire \(|A| = 1\). Les vecteurs peuvent être additionnés, multipliés par des constantes (y compris les nombres complexes) et multipliés entre eux. L’addition vectorielle fait correspondre une paire de vecteurs à un autre vecteur, plus précisément celui que l’on obtient en déplaçant le second vecteur de sorte que sa queue coïncide avec la pointe du premier, sans modifier la longueur ou la direction de l’un ou l’autre, puis en joignant la queue du premier à la pointe du second. Cette règle d’addition est connue sous le nom de loi du parallélogramme. Ainsi, par exemple, l’addition des vecteurs \(\ket{A}\) et \(\ket{B}\) donne le vecteur \(\ket{C} (= \ket{A} + \ket{B})\) comme dans la Figure 1 :
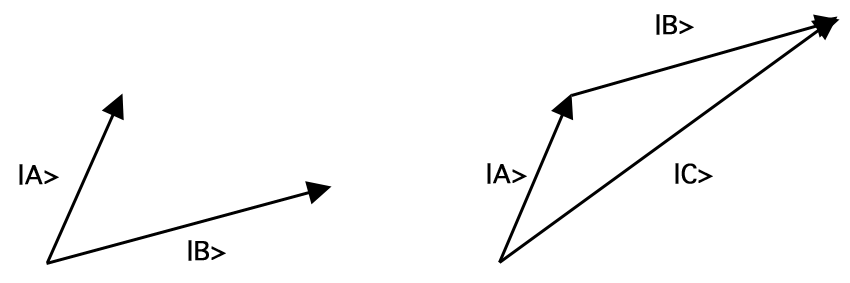
Figure 1.Addition de vecteurs
Multiplier un vecteur \(\ket{A}\) par \(n\), où \(n\) est une constante, donne un vecteur qui a la même direction que \(\ket{A}\) mais dont la longueur est \(n\) fois la longueur de \(\ket{A}\).
Dans un espace vectoriel réel, le produit (interne ou scalaire) d’une paire de vecteurs \(\ket{A}\) et \(\ket{B}\), écrit « \(\braket{A}{B}\) » est un scalaire égal au produit de leurs longueurs (ou « normes ») par le cosinus de l’angle,\(\theta\), entre eux :
Disons que \(\ket{A_1}\) et \(\ket{A_2}\) sont des vecteurs de longueur 1(« vecteurs unitaires ») tels que \(\braket{A_1}{A_2} = 0\). (L’angle entre ces deux vecteurs unitaires doit être de 90 degrés.) Nous pouvons alors représenter tout vecteur bidimensionnel \(\ket{B}\) en termes de nos vecteurs unitaires comme suit :
Par exemple, voici un graphique qui montre comment \(\ket{B}\) peut être représenté comme la somme des deux vecteurs unitaires \(\ket{A_1}\) et \(\ket{A_2}\) :
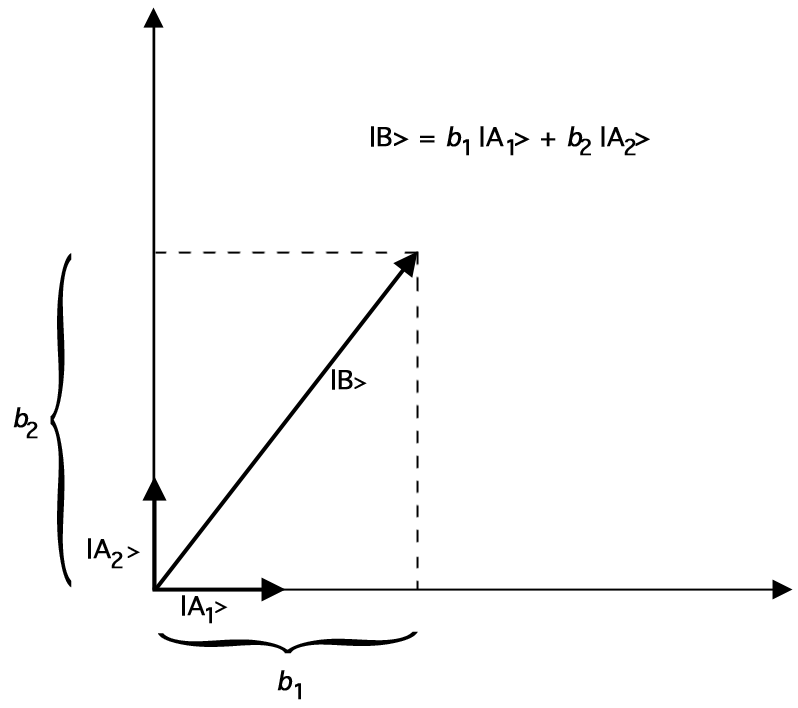
Figure 2.Représentation de \(\ket{B}\) par addition de vecteurs unitaires
Maintenant la définition du produit interne \(\braket{A}{B}\) doit être modifiée pour s’appliquer aux espaces complexes. Soit \(c^*\) le complexe-conjugué de \(c\). (Lorsque \(c\) est un nombre complexe de la forme \(a \pm bi\), alors le conjugué complexe \(c^*\) de \(c\) est défini comme suit:
\^* = a-bi \^* = a+bi\]
Donc, pour tous les nombres complexes \(c\), \(^* = c\),mais \(c^* = c\) juste au cas où \(c\) est réel.) Maintenant, la définition du produit interne de \(\ket{A}\) et \(\ket{B}\) pour les espaces complexes peut être donnée en termes de conjugués de coefficients complexes comme suit. Où \(\ket{A_1}\) et \(\ket{A_2}\) sont les vecteurs unitaires décrits précédemment, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}\) et \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}\), alors
\
La notion la plus générale et la plus abstraite d’un produit interne, dont nous avons maintenant défini deux cas particuliers, est la suivante. \(\braket{A}{B}\) est un produit interne sur un espace vectoriel \(V\) au cas où
- \(\braket{A}{A} = |A|^2\), et \(\braket{A}{A}=0\) si et seulement si \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}^*\)
- \(\braket{B}{A+C}=\braket{B}{A} + \braket{B}{C}\).
Il en résulte que
- la longueur de \(\ket{A}\) est la racine carrée du produit interne de \(\ket{A}\) avec lui-même, c’est-à-dire,\
et
- \(\ket{A}\) et \(\ket{B}\) sont mutuellement perpendiculaires, ou orthogonales, si, et seulement si, \(\braket{A}{B}\).
Un espace vectoriel est un ensemble de vecteurs fermés sous l’addition, et la multiplication par des constantes, un espace de produit interne est un espace vectoriel sur lequel l’opération de vectormultiplication a été définie, et la dimension d’un tel espace est le nombre maximum de vecteurs non nuls, mutuellement orthogonaux qu’il contient.
Toute collection de \(N\) vecteurs mutuellement orthogonaux de longueur 1 dans un espace vectoriel \(N\)-dimensionnel constitue une base orthonormale pour cet espace. Soit \(\ket{A_1}, \ldots, \ket{A_N}\) une telle collection de vecteurs unitaires. Alors chaque vecteur dans l’espace peut être exprimé comme une somme de la forme:
\
où \(b_i = \braket{B}{A_i}\). Les \(b_i\) sont ici connus comme les coefficients d’expansion de \(B\) dans la base \(A\).
Notez que :
- pour tous les vecteurs \(A\), \(B\), et \(C\) dans un espace donné,\
- pour tous les vecteurs \(M\) et \(Q\), exprimés en termes de la base \(A\),\
et
\
Il existe une autre façon d’écrire les vecteurs, à savoir en écrivant les coefficients d’expansion (par rapport à une base donnée) dans une colonne, commeo :
\
où \(q_i = \braket{Q}{A_i}\) et les \(A_i\) sont les vecteurs de base choisis.
Lorsqu’on a affaire à des espaces vectoriels de dimension infinie, comme on ne peut pas écrire toute la colonne des coefficients de dilatation nécessaires pour compléter un vecteur puisqu’elle devrait être infiniment longue, on écrit à la place la fonction (appelée « fonction d’onde » pour\(Q\), généralement représentée \(\psi(i))\) qui a ces coefficients comme valeurs. Nous écrivons, c’est-à-dire, la fonction :
\
Pour tout vecteur dans, et toute base pour, un espace vectoriel, nous pouvons obtenir la fonction d’onde du vecteur dans cette base ; et pour une fonction d’onde pour un vecteur, dans une base particulière, nous pouvons construire le vecteur dont c’est la fonction d’onde. Puisqu’il s’avère que la plupart des opérations importantes sur les vecteurs correspondent à des opérations algébriques simples sur leurs fonctions d’onde, c’est la façon habituelle de représenter les vecteurs d’état.
Lorsqu’une paire de systèmes physiques interagissent, ils forment un système composite, et, en mécanique quantique comme en mécanique classique, il existe une règle pour construire l’espace d’état d’un système composite à partir de ceux de ses composants, une règle qui nous dit comment obtenir, à partir des espaces d’état, \(H_A\) et \(H_B\) pour \(A\) et \(B\), respectivement, l’espace d’état – appelé le « produit tensoriel » de \(H_A\) et \(H_B\), et écrit \(H_A \otimes H_B\) – de la paire. Il y a deux choses importantes à propos de cette règle : premièrement, tant que \(H_A\) et \(H_B\) sont des espaces de Hilbert, \(H_A \otimes H_B\) le sera aussi, et deuxièmement, il y a certains faits concernant la façon dont \(H_A \otimes H_B\) se rapporte à \(H_A\) et \(H_B\), qui ont des conséquences surprenantes sur les relations entre le système complexe et ses parties. En particulier, il s’avère que l’état d’un système composite n’est pas uniquement défini par ceux de ses composants. Ce que cela signifie, ou du moins ce que cela semble signifier, c’est qu’il existe, selon la mécanique quantique, des faits concernant les systèmes composites (et pas seulement des faits concernant leur configuration spatiale) qui ne supervisent pas les faits concernant leurs composants ; cela signifie qu’il existe des faits concernant les systèmes en tant qu’ensembles qui ne supervisent pas les faits concernant leurs parties et la façon dont ces parties sont disposées. L’importance de cette caractéristique de la théorie ne peut être surestimée ; elle est, d’une manière ou d’une autre, impliquée dans la plupart de ses problèmes les plus difficiles.
En un peu plus de détails : si \(\{v_{i}^A\}\) est une base orthonormée pour \(H_A\) et \(\{u_{j}^B\}\) est une base orthonormée pour \(H_B\), alors l’ensemble des paires \((v_{i}^A, u_{j}^B)\) est considéré comme formant une base orthonormée pour l’espace du produit tensoriel \(H_A \otimes H_B\). La notation \(v_i^A \otimes u_j^B\) est utilisée pour la paire \((v_{i}^A,u_{j}^B)\), et le produit interne sur \(H_A \otimes H_B\)est défini comme :
\
Il résulte de cette construction que bien que chaque vecteur dans \(H_A \otimes H_B\) soit une somme linéaire de vecteurs exprimables sous la forme\(v^A \otimes u^B\), tous les vecteurs de l’espace ne sont pas eux-mêmes exprimables sous cette forme, et il s’avère que
- tout état composite définit uniquement les états de sescomposants.
- si les états de \(A\) et \(B\) sont purs (c’est-à-dire, représentables par les vecteurs \(v^A\) et \(u^B\),respectivement), alors l’état de \((A+B)\) est pur et représenté par\(v^A \otimes u^B\), et
- si l’état de \((A+B)\) est pur et exprimable sous la forme \(v^A \otimes u^B\), alors les états de \(A\) et de \(B\) sont purs, mais
- si les états de \(A\) et de \(B\) ne sont pas purs, c’est-à-dire quee., s’il s’agit d’états mixtes (ceux-ci sont définis ci-dessous), ils ne définissent pas de manière unique l’état de \((A+B)\) ; en particulier, il peut s’agir d’un état pur non exprimable sous la forme \(v^A \otimes u^B\).
2.2. Opérateurs
Un opérateur \(O\) est une application d’un espace vectoriel sur lui-même ; il prend tout vecteur \(\ket{B}\) dans un espace sur un autre vecteur \(\ket{B’}\) également dans l’espace ; \(O \ket{B} = \ket{B’}\). Les opérateurs linéaires sont des opérateurs qui ont les propriétés suivantes :
- \(O(\ket{A} + \ket{B}) = O \ket{A} O \ket{A} + O \ket{B}\), et
- \(O(c \ket{A}) = c(O \ket{A})\).
De même que tout vecteur dans un espace à \(N\)-dimension peut être représenté par une colonne de \(N\) nombres, par rapport à un choix de base pour l’espace, tout opérateur linéaire sur l’espace peut être représenté dans une notation en colonne par des \(N^2\) nombres :
\
où \(O_{ij} = \braket{A_i}{O \mid A_j}\) et les \(A_N\) sont les vecteurs de base de l’espace. L’effet de l’opérateur linéaire \(O\) sur le vecteur \(B\) est, alors, donné par
\
Deux autres définitions avant de pouvoir dire ce que sont les espaces de Hilbert, et ensuite nous pouvons nous tourner vers la mécanique quantique. \(\ket{B}\) est un vecteur propre de \(O\) avec la valeur propre \(a\) si, et seulement si, \(O \ket{B} = a \ket{B}\).Des opérateurs différents peuvent avoir des vecteurs propres différents, mais la relation vecteur propre/opérateur ne dépend que de l’opérateur et des vecteurs en question, et non de la base particulière dans laquelle ils sont exprimés ; la relation vecteur propre/opérateur est, c’est-à-dire, invariante sous changement de base. Un opérateur hermite est un opérateur qui a la propriété qu’il existe une base orthonormée constituée de ses vecteurs propres et que ces valeurs propres sont toutes réelles.
Un espace de Hilbert, enfin, est un espace vectoriel surlequel un produit interne est défini, et qui est complet, c’est-à-dire qui est tel que toute séquence de Cauchy de vecteurs dans l’espace converge vers avecteur dans l’espace. Tous les espaces à produit interne de dimension finie sont complets, et je me limiterai à ceux-ci. Le cas infiniinvoque certaines complications dans lesquelles il n’est pas fructueux d’entrer à ce stade.
Mécanique quantique
Quatre principes de base de la mécanique quantique sont :
(3.1)
États physiques.Tout système physique est associé à un espace de Hilbert, chaque vecteur unitaire dans l’espace correspond à un état pur possible du système, et chaque état pur possible, à un vecteur quelconque dans l’espace.
(3.2)
Garanties physiques.Les opérateurs hermitiens dans l’espace de Hilbert associé à un système représentent des quantités physiques, et leurs valeurs propres représentent les résultats possibles des mesures de ces quantités.
Il existe un opérateur, appelé hamiltonien, qui joue un rôle particulier dans la théorie quantique car la dynamique d’un système peut être commodément formulée en suivant son évolution. L’hamiltonien – écrit \(H\), ou \(\hat{H}\) – représente l’énergie totale du système. Ses valeurs propres sont les résultats possibles que l’on peut obtenir en mesurant l’énergie totale. Elle est donnée en additionnant les énergies cinétique et potentielle des composants du système.
(3.3)
Composition.L’espace de Hilbert associé à un système complexe est le produit tensoriel de ceux associés aux systèmes simples (dans la théorie standard, non relativiste : les particules individuelles) dont il est composé.
(3.4) Dynamique. a.
Contextes de type 1 : Étant donné l’état d’un système à\(t\) et les forces et contraintes auxquelles il est soumis, il existe une équation, la « séquation de Schrödinger », qui donne l’état à tout autre moment \(U\ket{v_t} \rightarrow \ket{v_{t’}}\). Les propriétés importantes de \(U\) pour nos objectifs sont qu’il est déterministe, c’est-à-dire qu’il transforme l’état d’un système à un moment donné en un état unique à tout autre moment, qu’il est unitaire, ce qui signifie qu’il est un automorphisme de l’espace de Hilbert sur lequel il agit (c’est-à-dire, (c’est-à-dire une application de cet espace sur lui-même qui préserve la structure spatiale linéaire et le produit interne), et elle est linéaire, c’est-à-dire que si elle prend un état \(\ket{A}\) sur l’état \(\ket{A’}\), et qu’elle prend l’état \(\ket{B}\) sur l’état \(\ket{B’}\), alors elle prend tout état de la forme \(\alpha \ket{A} + \beta \ket{B}\) sur l’état \(\alpha \ket{A’} + \beta \ket{B’}\).
b.
Contextes de type 2 (« Contextes de mesure »):Effectuer une « mesure » d’une observable \(B\) sur un système dans un état \(\ket{A}\) a pour effet d’effondrer le système dans un état propre \(B\) correspondant à la valeur propre observée. C’est ce qu’on appelle le postulat d’effondrement. Dans quel état \(B\)-propre particulier il s’effondre est une question de probabilité, et les probabilités sont données par une règle connue sous le nom de règle de Born :
\
Il y a deux points importants à noter concernant ces deux types de contextes :
- La distinction entre les contextes de type 1 et 2 reste à faire en termes de mécanique quantique ; personne n’a réussi à dire de façon complètement satisfaisante, dans les termes fournis par la théorie, quels sont les contextes de mesure, et
- Même si la distinction est faite, c’est une question d’interprétation ouverte de savoir s’il existe des contextes de type 2 ; c’est-à-dire que les contextes de type 1 sont des contextes de mesure.e., c’est une question interprétative ouverte de savoir s’il existe des contextes dans lesquels les systèmes sont régis par une règle dynamique autre que l’équation deSchrödinger.
Structures sur l’espace de Hilbert
J’ai remarqué plus haut que de la même manière que toute l’information que nous avons sur les relations entre les lieux d’une ville est incarnée dans les relations spatiales entre les points d’une carte qui les représentent, toute l’information que nous avons sur les relations internes entre (et entre) les états et les quantités en mécanique quantique est incarnée dans les relations mathématiques entre les vecteurs et les opérateurs qui les représentent. D’un point de vue mathématique, ce qui distingue vraiment la mécanique quantique de ses prédécesseurs classiques, c’est que les états et les quantités ont une structure plus riche ; ils forment des familles avec un réseau plus intéressant de relations entre leurs membres.
Toutes les caractéristiques physiquement conséquentes des comportements des systèmes de mécanique quantique sont des conséquences des propriétés mathématiques de ces relations, et les plus importantes d’entre elles sont facilement résumées:
(P1)
Toute façon d’additionner des vecteurs dans un espace de Hilbert ou de les multiplier par des scalaires donnera un vecteur qui est aussi dans cet espace. Dans le cas où le vecteur est normalisé, il représentera, d’après (3.1), un état possible du système, et dans le cas où il est la somme d’une paire de vecteurs propres d’une observable \(B\) avec des valeurs propres distinctes, il ne sera pas lui-même un vecteur propre de \(B\), mais seraassocié, d’après (3.4b), à un ensemble de probabilités de montrer un ou l’autre résultat dans les mesures de \(B\).
(P2)
Pour tout opérateur hermitien sur un espace de Hilbert, il en existe d’autres, sur le même espace, avec lesquels il ne partage pas un ensemble complet de vecteurs propres ; en effet, il est facile de montrer qu’il existe d’autres opérateurs de ce type avec lesquels il n’a aucun vecteur propre en commun.
Si nous faisons quelques hypothèses interprétatives supplémentaires, nous pouvons en dire plus. Supposons, par exemple, que
(4.1)
Chaque opérateur hermitien sur l’espace de Hilbertassocié à un système représente une observable distincte, et (donc)chaque vecteur normalisé, un état distinct, et
(4.2)
Un système a une valeur pour l’observable \(A\) si, et seulement si, le vecteur représentant son état est un état propre de l’opérateur \(A\). La valeur qu’il a, dans ce cas, est juste la valeur propre associée à cet état propre.
Il résulte de (P2), par (3.1), qu’aucun état de la mécanique quantique n’est un état propre de toutes les observables (et en effet qu’il existe des observables qui n’ont aucun état propre en commun), et donc, par (3.2), qu’aucun système mécanique quantique n’a jamais de valeurs simultanées pour toutes les grandeurs qui le concernent (et en fait qu’il existe des couples de grandeurs auxquels aucun état n’attribue de valeurs simultanées).
Il existe des opérateurs hermitiens sur le produit tensoriel\(H_1 \otimes H_2\) d’une paire d’espaces de Hilbert\(H_1\) et \(H_2\) … Dans le cas où \(H_1\) et \(H_2\) sont les espaces d’état des systèmes \(S1\) et \(S2\),\(H_1 \otimes H_2\) est l’espace d’état du système complexe \((S1+S2)\). Il en découle par (4.1) qu’il existe des observables appartenant à \((S1+S2)\) dont les valeurs ne sont pas déterminées par les valeurs des observables appartenant aux deux individuellement.
Ce sont toutes des conséquences directes de la prise de vecteurs et d’opérateurs dans l’espace de Hilbert pour représenter, respectivement, des états et des observables, et de l’application de la règle de Born (et plus tard (4.1) et (4.2)), pour donner une signification empirique aux affectations d’état. Cette partie est parfaitement bien comprise ; la véritable difficulté de la compréhension de la mécanique quantique réside dans la maîtrise de ses implications – physiques, métaphysiques et épistémologiques.
Quiconque essaie de comprendre ce que la mécanique quantique dit du monde doit se débattre avec un fait restant. Ceproblème ne concerne pas les espaces de Hilbert, mais la dynamique – les règles qui décrivent les trajectoires que les systèmes suivent à travers l’espace. D’un point de vue physique, ce problème est bien plus grave que tout ce qui a été discuté jusqu’à présent. Non seulement elle présente des difficultés pour quelqu’un qui essaie de fournir une interprétation de la théorie, mais elle semble également indiquer une incohérence logique dans les fondements de la théorie.
Supposons que nous ayons un système \(S\) et un dispositif \(S^*\) qui mesure une observable \(A\) sur \(S\) avec des valeurs \(\{a_1,a_2, a_3, …\}\). Il existe alors un état de \(S^*\) (l' »état fondamental »), et une observable \(B\)avec des valeurs \(\{b_1, b_2, b_3, …\}\) appartenant à \(S^*\) (son « observable de l’aiguille », appelée ainsi parce que c’est ce qui joue le rôle de l’aiguille sur un cadran à l’avant d’un instrument de mesure schématique en enregistrant le résultat de l’expérience), qui sont telles que, si \(S^*\) est lancé dans son état fondamental et interagit de manière appropriée avec \(S\), et si la valeur de \(A\) immédiatement avant l’interaction est \(a_1\), alors la valeur de \(B\) immédiatement après est \(b_1\). Si, par contre, la valeur de \(A\) immédiatement avant l’interaction est \(a_2\), alors la valeur de \(B\) immédiatement après est \(b_2\) ; si la valeur de \(A\) immédiatement avant l’interaction est \(a_3\), alors la valeur de \(B\) immédiatement après est \(b_3\), et ainsi de suite. C’est exactement ce que cela signifie de dire que \(S^*\) mesure \(A\). Donc, si nous représentons l’état partiel conjoint de \(S\) et \(S^*\) (juste la partie qui spécifie la valeur de , l’observable dont les valeurs correspondent aux affectations conjointes de valeurs à l’observable mesuré sur \(S\) et à l’observable pointeur sur \(S^*\)) par le vecteur\(\ket{A=a_i}_s \ket{B=b_i}_{s^*}\), et que « \(\rightarrow\) « représente la description dynamique de l’interaction entre les deux, dire que \(S^*\) est un instrument de mesure pour \(A\) c’est dire que les lois dynamiques impliquent que,
\
et ainsi de suite.
Intuitivement, \(S^*\) est un instrument de mesure pour une \(A\) observable juste au cas où il y a une certaine caractéristique observable de \(S^*\) (peu importe quoi, juste quelque chose dont les valeurs peuvent être vérifiées en regardant l’appareil), qui est corrélée avec les valeurs de \(A\) des systèmes alimentés en lui de telle manière que nous pouvons lire ces valeurs sur l’état observable de \(S^*\) après l’interaction. En langage philosophique, \(S^*\) est un instrument de mesure de \(A\) juste au cas où il y a une certaine caractéristique observable de \(S^*\) qui suit ou indique les valeurs de \(A\) des systèmes avec lesquels il interagit d’une manière appropriée.
Maintenant, il découle de (3.1), ci-dessus, qu’il existe des états de \(S\) (trop nombreux pour être comptés) qui ne sont pas des états propres de \(A\), et si nous considérons ce que l’équation de Schrödinger nous dit sur l’évolution conjointe de \(S\) et \(S^*\) lorsque \(S\) est démarré dans l’un de ceux-ci, nous trouvons que l’état de la paire après interaction est une superposition d’états propres de . Peu importe quelle observable sur \(S\) est mesurée, et peu importe dans quelle superposition particulière \(S\) commence ; lorsqu’il est introduit dans un instrument de mesure de cette observable,si l’interaction est correctement décrite par la séquation de Schrödinger, il s’ensuit juste de la linéarité du \(U\) dans cette équation,l’opérateur qui effectue la transformation de l’état antérieur à l’état postérieur de la paire, que l’état conjoint de \(S\) et de l’appareil après l’interaction est une superposition des états propres de cette observable sur le système conjoint.
Supposons, par exemple, que nous commençons \(S^*\) dans son état fondamental, et \(S\) dans l’état
\
C’est une conséquence des règles pour obtenir l’espace d’état du système composite que l’état combiné de la paire est
\
et cela découle du fait que \(S^*\) est un instrument de mesure pour \(A\),et de la linéarité de \(U\) que leur état combiné après interaction, est
Ceci, cependant, est incompatible avec la règle dynamique pour les contextes de type 2, car la règle dynamique pour les contextes de type 2 (et s’il existe de tels contextes, celui-ci en est un) implique que l’état de la paire après interaction est soit
\
soit
\
En effet, elle implique qu’il existe une probabilité précise de \(\frac{1}{2}\) qu’elle se retrouve dans le premier cas, et une probabilité de \(\frac{1}{2}\) qu’elle se retrouve dans le second.
On peut essayer de rétablir la cohérence logique en renonçant à la règle dynamique pour les contextes de type 2 (ou, ce qui revient au même, en niant l’existence de tels contextes), mais on se heurte alors au problème de la cohérence avec l’expérience. En effet, ce n’est pas par hasard que cette règle a été incluse dans la théorie ; nous savons à quoi ressemble un système lorsqu’il est dans un état propre d’une observable donnée, et nous savons par expérience que l’appareil de mesure après mesure est dans un état propre de l’observable pointeur. Et donc nous savons dès le départ que si une théorie nous dit autre chose sur les états post-mesure des appareils de mesure, quel que soit cet autre chose, c’est faux.
C’est, en un mot, le problème de la mesure en mécanique quantique ; toute interprétation de la théorie, toute histoire détaillée sur ce qu’est le monde selon la mécanique quantique, et enparticulier ces morceaux de monde dans lesquels les mesures se déroulent, doit s’y colleter.
Loose Ends
Les états mixtes sont des sommes pondérées d’états purs, etils peuvent être utilisés pour représenter les états d’ensembles dont les composants sont dans différents états purs, ou les états de systèmes individuels dont nous n’avons qu’une connaissance partielle. Dans le premier cas, le poids attaché à un état pur donné reflète la taille de la composante de l’ensemble qui est dans cet état (et donc la probabilité objective qu’un membre arbitraire de l’ensemble le soit) ; dans le second cas, ils reflètent la probabilité épistémique que le système en question auquel l’état est attribué soit dans cet état.
Si nous ne voulons pas perdre la distinction entre les états purs et les états mixtes, nous avons besoin d’une manière de représenter la somme pondérée d’un ensemble d’états purs (de manière équivalente, des fonctions de probabilité qui leur sont associées) qui soit différente de l’addition des vecteurs (convenablement pondérés) qui les représentent, et cela signifie que nous avons besoin soit d’une autre manière de représenter les états mixtes, soit d’une manière uniforme de représenter à la fois les états purs et les états mixtes qui préserve la distinction entre eux.Il existe un type d’opérateur dans les espaces de Hilbert, appelé opérateur de densité, qui remplit bien cette dernière fonction, et il n’est pas difficile de reformuler tout ce qui a été dit sur les vecteurs d’état en termes d’opérateurs de densité. Ainsi, même s’il est courant de parler comme si les états purs étaient représentés par des vecteurs, la règle officielle est que les états – purs ou mixtes – sont représentés en mécanique quantique par des opérateurs de densité.
Bien que les états mixtes puissent, comme je l’ai dit, être utilisés pour représenter notre ignorance des états de systèmes qui sont en fait dans l’un ou l’autre état pur, et bien que cela ait semblé à beaucoup une manière adéquate d’interpréter les mélanges dans des contextes classiques, il y a de sérieux obstacles à l’appliquer généralement aux mélanges de la mécanique quantique. Tout ce qui a été dit sur les observables, à proprement parler, ne s’applique qu’au cas où les valeurs de l’observable forment un ensemble discret ; les subtilités mathématiques qui sont nécessaires pour le généraliser au cas des observables continues sont compliquées et soulèvent des problèmes de nature plus technique. Il est préférable de laisser ces problèmes pour une discussion détaillée.
Ceci devrait être la préparation initiale dont on a besoin pour aborder la discussion philosophique de la mécanique quantique, mais ce n’est qu’un premier pas. Plus on en apprend sur les relations entre et parmi les vecteurs et les opérateurs dans l’espace de Hilbert, sur la façon dont les espaces des systèmes simples sont liés à ceux des systèmes complexes, et sur l’équation qui décrit comment les vecteurs d’état se déplacent dans l’espace, plus on appréciera à la fois la nature et la difficulté des problèmes associés à la théorie. Ce qui est amusant avec la mécanique quantique, ce qui la rend infiniment absorbante pour un philosophe, c’est que plus on apprend, plus les problèmes deviennent difficiles.