Kvantmekanik
Terminologi
Fysiska system delas in i olika typer beroende på deras oföränderliga (eller ”tillståndsoberoende”) egenskaper, och tillståndet hos ett system vid en viss tidpunkt består av en fullständig specifikation av de av dess egenskaper som förändras med tiden (dess ”tillståndsberoende” egenskaper). För att ge en fullständig beskrivning av ett system måste vi alltså säga vilken typ av system det är och vilket tillstånd det har vid varje tidpunkt i sin historia.
En fysikalisk kvantitet är en ömsesidigt uteslutande och gemensamt uttömmande familj av fysikaliska egenskaper (för dem som känner till detta sätt att tala är det en familj av egenskaper med strukturen av cellerna i en skiljevägg). Genom att veta vilka typer av värden en kvantitet har kan vi få veta en hel del om förhållandena mellan de egenskaper som den är sammansatt av. Värdena för en bivalent kvantitet, till exempel, bildar en mängd med två medlemmar; värdena för en realvärdeskvantitet bildar en mängd med de reella talens struktur. Detta är ett specialfall av något som vi kommer att se om och om igen, nämligen,att vetskapen om vilken typ av matematiska objekt som representerar elementen i en viss mängd (här värdena för en fysikalisk kvantitet, senare de tillstånd som ett system kan anta, eller de kvantiteter som hör till det) säger oss mycket mycket (ja, förmodligen allt som finns att veta) om relationerna mellan dem.
I kvantmekaniska sammanhang används begreppet ”observerbar” omväxlande med ”fysikalisk kvantitet”, och det bör behandlas som en teknisk term med samma innebörd. Det är ingen tillfällighet att de tidiga utvecklarna av teorin valde denna term, men valet gjordes av skäl som numera inte är allmänt accepterade. Ett systems tillståndsutrymme är det utrymme som utgörs av mängden av dess möjliga tillstånd, dvs. de fysiskt möjliga sätten att kombinera värdena på de storheter som kännetecknar det internt. I klassiska teorier betecknas en uppsättning storheter som utgör en superveniensbas för resten vanligen som ”grundläggande” eller ”fundamental”, och eftersom varje matematiskt möjligt sätt att kombinera deras värden är en fysisk möjlighet, kan tillståndsrummet erhållas genom att helt enkelt ta dessa som koordinater. Tillståndsrummet för ett klassiskt mekaniskt system bestående av \(n\) partiklar, som erhålls genom att ange värdena för\(6n\) realvärderade storheter – tre positionskomponenter och tre rörelsemängdskomponenter för varje partikel i systemet – är ett\(6n\)-dimensionellt koordinatrum. Varje möjligt tillstånd i ett sådant system motsvarar en punkt i rummet, och varje punkt i rummet motsvarar ett möjligt tillstånd i ett sådant system. Situationen är lite annorlunda inom kvantmekaniken, där det finns matematiskt beskrivbara sätt att kombinera värdena för de kvantiteter som inte representerar fysiskt möjliga tillstånd. Som vi kommer att se är kvantmekanikens tillståndsrum speciella typer av vektorrum, så kallade Hilbert-rum, och de har mer inre struktur än sina klassiska motsvarigheter.
En struktur är en uppsättning element på vilka vissa operationer och relationer är definierade, en matematisk struktur är bara en struktur där elementen är matematiska objekt (tal, uppsättningar, vektorer) och operationerna är matematiska och en modell är en matematisk struktur som används för att representera någon fysikaliskt viktig struktur i världen.
Kvantmekanikens hjärta och själ finns i de Hilbert-rum som representerar de kvantmekaniska systemens tillståndsrum.De interna relationerna mellan tillstånd och kvantiteter, och allt detta innebär om hur kvantmekaniska system beter sig, är alla invävda i strukturen hos dessa rum, förkroppsligade i relationerna mellan de matematiska objekt som representerar dem. Detta innebär att förståelsen av hur ett system är enligt kvantmekaniken är oskiljaktig från att känna till den interna strukturen hos dessa rum. Om man känner till Hilbertrymden och blir bekant med de dynamiska lagar som beskriver de vägar som vektorerna färdas genom den, vet man allt som finns att veta, i de termer som teorin tillhandahåller, om de system som den beskriver.
Med ”känna till Hilbertrymden” menar jag något mer än att ha en beskrivning eller en karta över den; alla som har en lärobok i kvantmekanik i sin hylla har det. Jag menar att man känner till den på samma sätt som man känner till den stad man bor i. Detta är en praktisk typ av kunskap som kommer i flera steg och som man bäst förvärvar genom att lära sig att lösa problem av denna typ: Hur tar jag mig från A till B? Kan jag ta mig dit utan att passera genom C? Och vilken är den kortaste vägen? Doktorander i fysik tillbringar långa år med att bli förtrogna med Hilbert-rummets vrår och vrår, lokalisera välkända landmärken, beträda dess upptrampade stigar, lära sig var hemliga passager och återvändsgränder finns, och utveckla en känsla för hur det hela ser ut. De lär sig att navigera i Hilbert-rummet på samma sätt som en taxichaufför lär sig att navigera i sin stad.
Hur mycket av denna typ av kunskap behövs för att närma sig de filosofiska problem som är förknippade med teorin? I början inte särskilt mycket: bara de mest allmänna fakta om landskapets geometri (som i alla fall, till skillnad från de flesta städer, är vackert organiserad) och de vägar som (de vektorer som representerar systemens tillstånd) färdas genom dem. Det är detta som kommer att introduceras här: först lite enkel matematik och sedan, i ett nötskal, teorin.
Matematik
2.1 Vektorer och vektorrum
En vektor \(A\), som skrivs \(\(\ket{A}\)) är ett matematiskt objekt som kännetecknas av en längd, \(|A|\), och en riktning. En anormaliserad vektor är en vektor med längden 1, dvs. \(|A| = 1\). Vektorer kan adderas, multipliceras med konstanter (inklusive komplexa tal) och multipliceras med varandra. Vektoraddition mappar varje par av vektorer till en annan vektor, närmare bestämt den som du får genom att flytta den andra vektorn så att dess svans sammanfaller med den första vektorns spets, utan att ändra längden eller riktningen på någon av dem, och sedan sammanfoga den första vektorns svans med den andra vektorns spets. Denna additionsregel är känd som parallellogramlagen. Om man till exempel adderar vektorerna \(\ket{A}\) och \(\ket{B}\) får man vektorn \(\ket{C}). (= \ket{A} + \ket{B})\) enligt figur 1:
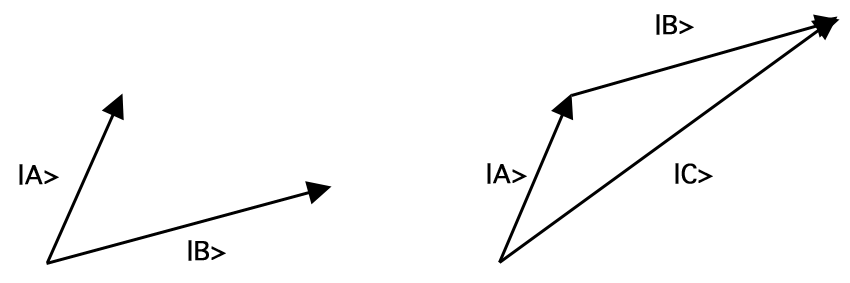
Figur 1.Vektoraddition
Multiplicering av en vektor \(\ket{A}\) med \(n\), där \(n\) är konstant, ger en vektor som har samma riktning som \(\ket{A}\) men vars längd är \(n\) gånger \(\ket{A}\)’s längd.
I ett reellt vektorrum är den inre produkten (eller punktprodukten) av ett vektorpar \(\ket{A}\) och \(\ket{B}\), som skrivs \(\(\braket{A}{B}\)), en skalär som är lika med produkten av deras längder (eller ”normer”) gånger cosinus av vinkeln \(\theta\), mellan dem:
Låt \(\ket{A_1}\) och \(\ket{A_2}\) vara vektorer med längden 1 (”enhetsvektorer”) så att \(\(\braket{A_1}{A_2}{A_2} = 0\). (Vinkeln mellan dessa två enhetsvektorer måste vara 90 grader.) Då kan vi representera varje tvådimensionell vektor \(\ket{B}\) i termer av våra enhetsvektorer på följande sätt:
\
Här är till exempel en graf som visar hur \(\ket{B}\) kan representeras som summan av de två enhetsvektorerna \(\ket{A_1}\) och \(\ket{A_2}\):
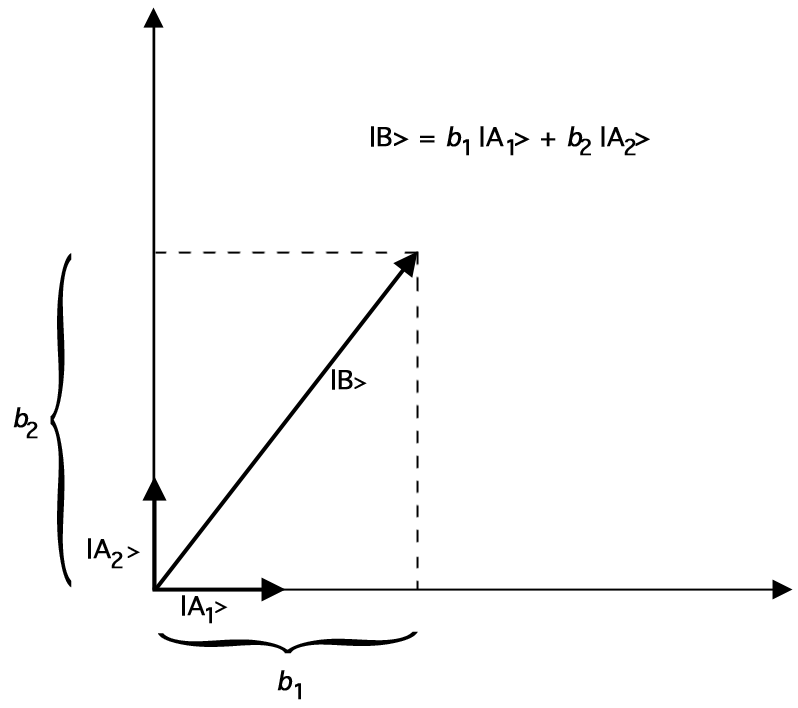
Figur 2.Representation av \(\ket{B}\) genom vektoraddition av enhetsvektorer
Nu måste definitionen av den inre produkten \(\braket{A}{B}\) ändras så att den gäller för komplexa rum. Låt \(c^*\) vara den komplexa konjugerade delen av \(c\). (När \(c\) är ett komplext tal av formen \(a \pm bi\), definieras det komplexa konjugatet\(c^*\) till \(c\) på följande sätt:
\^* = a-bi \\^* = a+bi\]
För alla komplexa tal \(c\) gäller alltså \(^* = c\), men \(c^* = c\) bara för det fall \(c\) är verkligt.) Definitionen av den inre produkten av \(\ket{A}\) och \(\ket{B}\) för komplexa rum kan nu ges i termer av konjugerade komplexa koefficienter enligt följande. Där \(\ket{A_1}\) och \(\ket{A_2}\) är de tidigare beskrivna enhetsvektorerna, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}\) och \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}\), då
\
Det mest allmänna och abstrakta begreppet för en inre produkt, som vi nu har definierat två specialfall av, är följande. \(\braket{A}{B}\) är en inre produkt på ett vektorrum \(V\) just i det fall
- \(\braket{A}{A}{A} = |A|^2\), och \(\braket{A}{A}=0\) om och endast om \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}{B}^*\)
- \(\braket{B}{A+C}=\braket{B}{A}{A} + \braket{B}{C}\).
Det följer av detta att
- längden av \(\ket{A}\) är kvadratroten av innerprodukten av \(\ket{A}\) med sig själv, dvs,\
och
- \(\ket{A}\) och \(\ket{B}\) är vinkelräta mot varandra, eller ortogonala, om, och endast om, \(\braket{A}{B}\).
En vektorrymd är en uppsättning vektorer som är slutna under addition och multiplikation med konstanter, en inre produktrymd är en vektorrymd där operationen för vektormultiplikation har definierats, och dimensionen av en sådan rymd är det maximala antalet icke-noll, ömsesidigt ortogonala vektorer som den innehåller.
En samling av \(N\) ömsesidigt ortogonala vektorer av längd 1 i ett\(N\)-dimensionellt vektorrum utgör en ortonormal bas för det rummet. Låt \(\ket{A_1}, \ldots, \ket{A_N}\) vara en sådan samling av enhetsvektorer. Då kan varje vektor i utrymmet uttryckas som en summa av formen:
\
varvid \(b_i = \braket{B}{A_i}\). \(b_i\) är här kända som \(B\)s expansionskoefficienter i \(A\)-basen.
Visa att:
- för alla vektorer \(A\), \(B\) och \(C\) i ett givet rum,\
- för alla vektorer \(M\) och \(Q\), uttryckt i termer av \(A\)-basen,\
och
\
Det finns ett annat sätt att skriva vektorer, nämligen genom att skriva expansionskoefficienterna (i förhållande till en given bas) i en kolumn, till exempel:
\
där \(q_i = \braket{Q}{A_i}\) och \(A_i\) är de valda basvektorerna.
När vi har att göra med vektorrum av oändlig dimension, eftersom vi inte kan skriva hela kolumnen med expansionskoefficienter som behövs för att peka ut en vektor eftersom den skulle bli oändligt lång, så skriver vi i stället ner den funktion (kallad ”vågfunktion” för\(Q\), vanligen representerad \(\psi(i))\) som har dessa koefficienter som värden. Vi skriver ner funktionen:
\
Genom en vektor i, och en bas för, ett vektorrum kan vi få fram vektorns vågfunktion i den basen, och genom att ge en vågfunktion för en vektor i en viss bas kan vi konstruera den vektor vars vågfunktion det är. Eftersom det visar sig att de flesta viktiga operationer på vektorer motsvarar enkla algebraiska operationer på deras vågfunktioner, är detta det vanliga sättet att representera statsvektorer.
När ett par fysiska system interagerar bildar de ett sammansatt system, och inom kvantmekaniken liksom inom den klassiska mekaniken finns det en regel för att konstruera ett sammansatt systems tillståndsrum från dess komponenters tillståndsrum, En regel som talar om för oss hur vi från de två tillståndsrummen \(H_A\) och \(H_B\) för \(A\) respektive \(B\) ska få fram tillståndsrummet – som kallas ”tensorprodukten” av \(H_A\) och \(H_B\), och som skrivs \(H_A \otimes H_B\) – för paret. Det finns två viktiga saker med regeln; för det första, så länge \(H_A\) och \(H_B\) är Hilbert-rum, kommer \(H_A \otimes H_B\) också att vara det, och för det andra finns det några fakta om hur \(H_A \otimes H_B\) förhåller sig till \(H_A\) och \(H_B\), som har överraskande konsekvenser för relationerna mellan det komplexa systemet och dess delar. I synnerhet visar det sig att tillståndet i ett sammansatt system inte entydigt definieras av tillstånden i dess delar. Vad detta betyder, eller åtminstone vad det verkar betyda, är att det enligt kvantmekaniken finns fakta om sammansatta system (och inte bara fakta om deras rumsliga konfiguration) som inte är överordnade fakta om deras komponenter; det betyder att det finns fakta om system som helhet som inte är överordnade fakta om deras delar och det sätt på vilket dessa delar är arrangerade i rymden. Betydelsen av denna egenskap hos teorin kan inte överdrivas; den är på ett eller annat sätt inblandad i de flesta av teorins svåraste problem.
Lite mer detaljerat: Om \(\(\{v_{{i}^A\}\) är en ortonormal bas för \(H_A\) och \(\(\{u_{j}^B\}\) är en ortonormal bas för \(H_B\), så anses uppsättningen av par \((v_{i}^A, u_{j}^B)\) bilda en ortonormal bas för tensorproduktutrymmet \(H_A \otimes H_B\). Beteckningen \(v_i^A \otimes u_j^B\) används för paret \((v_{i}^A,u_{j}^B)\), och inre produkt på \(H_A \otimes H_B\) definieras som:
\
Det är ett resultat av denna konstruktion att även om varje vektor i\(H_A \otimes H_B\) är en linjär summa av vektorer som kan uttryckas i formen\(v^A \otimes u^B\), så är inte varje vektor i utrymmet själv uttryckbar i den formen, och det visar sig att
- något sammansatt tillstånd unikt definierar tillstånden för sina komponenter.
- Om tillstånden för \(A\) och \(B\) är rena (dvs, representeras av vektorerna \(v^A\) och \(u^B\), så är tillståndet \((A+B)\) rent och representeras av \(v^A \otimes u^B\), och
- om tillståndet i \((A+B)\) är rent och kan uttryckas i formen \(v^A \otimes u^B\), då är tillstånden \(A\) och \(B\) rena, men
- om tillstånden \(A\) och \(B\) inte är rena, dvs.e., om de är blandade tillstånd (dessa definieras nedan), definierar de inte entydigt tillståndet \((A+B)\); i synnerhet kan det vara ett rent tillstånd som inte kan uttryckas i formen \(v^A \otimes u^B\).
2.2 Operatorer
En operatör \(O\) är en avbildning av ett vektorrum på sig själv; den tar varje vektor \(\ket{B}\) i ett rum till en annan vektor \(\ket{B’}\) också i rummet; \(O \ket{B} = \ket{B’}\). Linjära operatörer är operatörer som har följande egenskaper:
- \(O(\ket{A} + \ket{B}) = O \ket{A}
- \(O(c \ket{A}) = c(O \ket{A})\).
Såsom varje vektor i ett \(N\)-dimensionellt rum kan representeras av en kolumn av \(N\)-tal, i förhållande till ett val av bas för rummet, kan varje linjär operatör på rummet representeras i en kolumnnotering av \(N^2\)-tal:
\
där \(O_{ij} = \braket{A_i}{O \mid A_j}\) och \(A_N\) är rummets basvektorer. Effekten av den linjära operatören \(O\) på vektorn\(B\) ges då av
\
Två definitioner till innan vi kan säga vad Hilbertrymder är, och sedan kan vi övergå till kvantmekanik. \(\ket{B}\) är en egenvektor till \(O\) med egenvärdet \(a\) om, och endast om, \(O \ket{B} = a \ket{B}\).Olika operatörer kan ha olika egenvektorer, men förhållandet mellan egenvektor och operatör beror endast på operatören och vektorerna i fråga, och inte på den särskilda bas i vilken de uttrycks; förhållandet mellan egenvektor och operatör är, det vill säga, invariant vid byte av bas. En hermitisk operatör är en operatör som har egenskapen att det finns en ortonormal bas som består av dess egenvektorer och att dessa egenvärden alla är verkliga.
En Hilbertrymd är slutligen en vektorrymd där en inre produkt är definierad och som är fullständig, dvs. som är sådan att varje Cauchy-sekvens av vektorer i rummet konvergerar till en vektor i rummet. Alla finitdimensionella inre produktrum är kompletta, och jag kommer att begränsa mig till dessa. Det oändliga fallet innebär vissa komplikationer som det inte är fruktbart att gå in på i detta skede.
Kvantmekanik
Fyra grundläggande principer för kvantmekanik är:
(3.1)
Fysiska tillstånd: Varje fysiskt system är associerat med ett Hilbert-rum, varje enhetsvektor i rummet motsvarar ett möjligt rent tillstånd hos systemet, och varje möjligt rent tillstånd motsvarar någon vektor i rummet.
(3.2)
Fysiska storheter: Hermitiska operatorer i Hilbert-rummet som är associerat med ett system representerar fysiska storheter, och deras egenvärden representerar de möjliga resultaten av mätningar av dessa storheter.
Det finns en operatör, kallad Hamiltonianen, som spelar en särskild roll i kvantteorin eftersom ett systems dynamik kan formuleras på ett smidigt sätt genom att följa dess utveckling. Hamiltonianen – som skrivs \(H\), eller \(\hat{H}\) – står för systemets totala energi. Dess egenvärden är de möjliga resultat som kan erhållas vid mätningar av den totala energin. Den ges genom att summera de kinetiska och potentiella energierna hos systemets komponenter.
(3.3)
Sammansättning: Det Hilbertrum som är förknippat med ett komplext system är tensorprodukten av dem som är förknippade med de enkla system (i den standardiserade, icke-relativistiska teorin: de enskilda partiklarna) som det är sammansatt av.
(3.4) Dynamik. a.
Sammanhang av typ 1: Givet ett systems tillstånd vid\(t\) och de krafter och begränsningar som det är utsatt för, finns det en ekvation, ”Schrödingers sekvens”, som ger tillståndet vid varje annan tidpunkt \(U\ket{v_t} \rightarrow \{v_{t’}}\). De viktiga egenskaperna hos \(U\) för våra syften är att den är deterministisk, det vill säga att den omvandlar ett systems tillstånd vid en tidpunkt till ett unikt tillstånd vid varje annan tidpunkt, att den är enhetlig, det vill säga att den är en automorfism av det Hilbert-rum som den verkar på (dvs, Det är en Hilbert-mekanism, dvs. en överföring av det utrymmet på sig självt som bevarar den linjära rymdstrukturen och den inre produkten, och den är linjär, vilket innebär att om den tar ett tillstånd \(\ket{A}\) till tillståndet \(\ket{A’}\), och tar tillståndet \(\ket{B}\) till tillståndet \(\ket{B’}\), så tar den varje tillstånd av formen \(\alpha \ket{A} +\beta \ket{B}\) till tillståndet \(\alpha \ket{A’} + \beta \ket{B’}\).
b.
Sammanhang av typ 2 (”mätningssammanhang”): Att utföra en ”mätning” av en observerbar \(B\) på ett system i ett tillstånd \(\ket{A}\) har effekten att systemet kollapsar till ett \(B\)-eigentillstånd som motsvarar det observerade egenvärdet. Detta är känt som kollapspostulatet. Vilket \(B\)-eigentillstånd det kollapsar till är en fråga om sannolikhet, och sannolikheterna ges av en regel som kallas Borns regel:
\
Det finns två viktiga punkter att notera om dessa två typer av sammanhang:
- Den kvantmekaniska distinktionen mellan sammanhang av typ 1 och 2 återstår att klargöra; ingen har lyckats säga på ett helt tillfredsställande sätt, i de termer som teorin tillhandahåller, vilka sammanhang som är mätkontexter, och
- Även om distinktionen klargörs är det en öppen tolkningsfråga om det finns sammanhang av typ 2, dvs.e., det är en öppen tolkningsfråga om det finns några sammanhang där system styrs av en annan dynamisk regel än Skrödingers ekvation.
Strukturer på Hilbert Space
Jag anmärkte ovan att på samma sätt som all den information vi har om relationerna mellan platser i en stad är förkroppsligad i de rumsliga relationerna mellan de punkter på en karta som representerar dem, så är all den information vi har om de interna relationerna mellan (och mellan) tillstånd och storheter i kvantmekaniken förkroppsligad i de matematiska relationerna mellan de vektorer och operatörer som representerar dem. Ur matematisk synvinkel är det som verkligen skiljer kvantmekaniken från dess klassiska föregångare att tillstånden och storheterna har en rikare struktur; de bildar familjer med ett mer intressant nätverk av relationer mellan medlemmarna.
Alla de fysikaliska konsekvenserna av beteendena hos kvantmekaniska system är konsekvenser av matematiska egenskaper hos dessa relationer, och de viktigaste av dem kan enkelt sammanfattas:
(P1)
Varje sätt att addera vektorer i en Hilbert-rymd eller multiplicera dem med skalarer kommer att ge en vektor som också finns i denna rymd. Om vektorn är normaliserad kommer den, enligt (3.1), att representera ett möjligt tillstånd i systemet, och om den är summan av ett par egenvektorer av en observerbar \(B\) med distinkta egenvärden, kommer den i sig själv inte att vara en egenvektor av \(B\), utan kommer enligt (3.4b) att vara associerad med en uppsättning sannolikheter för att visa det ena eller det andra resultatet i \(B\)-mätningar.
(P2)
För varje hermitisk operatör på ett Hilbert-rum finns det andra, på samma rum, med vilka den inte delar en fullständig uppsättning egenvektorer; det är i själva verket lätt att visa att det finns andra sådana operatörer med vilka den inte har några egenvektorer gemensamt.
Om vi gör ett par ytterligare tolkningsantaganden kan vi säga mer. Anta till exempel att
(4.1)
Varje hermitisk operatör på Hilbertrymden som är associerad med ett system representerar en distinkt observerbar, och (därmed)varje normaliserad vektor, ett distinkt tillstånd, och
(4.2)
Ett system har ett värde för den observerbara \(A\) om, och endast om, den vektor som representerar dess tillstånd är en egenstat av \(A\)-operatorn. Värdet som det har i ett sådant fall är bara det egenvärde som är associerat med detta egentillstånd.
Det följer av (P2), genom (3.1), att inget kvantmekaniskt tillstånd är ett egentillstånd för alla observabler (och att det faktiskt finns observabler som inte har några gemensamma egentillstånd), och därför, genom (3.2), att inget kvantmekaniskt system någonsin har samtidiga värden för alla storheter som hör till det (och att det faktiskt finns par av storheter som inget tillstånd tilldelar samtidiga värden).
Det finns hermitiska operatörer på tensorprodukten\(H_1 \otimes H_2\) av ett par Hilbertrymder\(H_1\) och \(H_2\) … Om \(H_1\) och \(H_2\) är tillståndsrummen för systemen \(S1\) och \(S2\), är \(H_1 \otimes H_2\) tillståndsrummet för det komplexa systemet \((S1+S2)\). Av detta följer genom (4.1) att det finns observabler som hör till \((S1+S2)\) vars värden inte bestäms av värdena för observabler som hör till de två enskilda systemen.
Detta är alla enkla konsekvenser av att man tar vektorer och operatörer i Hilbert-rummet som representanter för tillstånden respektive observablerna och att man tillämpar Borns regel (och senare (4.1) och (4.2)), för att ge tillståndstilldelningarna en empirisk innebörd. Den verkliga svårigheten när det gäller att förstå kvantmekaniken är att komma till rätta med dess implikationer – fysiska, metafysiska och epistemologiska.
Var och en som försöker komma till rätta med vad kvantmekaniken säger om världen måste ta itu med ett återstående faktum. Detta problem handlar inte om Hilbert-rummen, utan om dynamiken – de regler som beskriver de banor som systemen följer genom rummet. Ur fysikalisk synvinkel är det mycket mer bekymmersamt än allt som diskuterats hittills. Det innebär inte bara svårigheter för någon som försöker ge en tolkning av teorin, utan tycks också peka på en logisk inkonsekvens i teorins grunder.
Antag att vi har ett system \(S\) och en anordning \(S^*\) som mäter en observerbar \(A\) på \(S\) med värden \(\{a_1,a_2,a_3, …\}\). Då finns det ett tillstånd på \(S^*\) (grundtillståndet) och en observabel \(B\) med värden \(\{b_1, b_2, b_3, …\}\\\) som hör till \(S^*\) (dess ”pekarobservabel”, som kallas så eftersom det är det som spelar rollen som pekaren på en ratt på framsidan av ett schematiskt mätinstrument när det gäller att registrera resultatet av experimentet), som är sådana att om \(S^*\) startas i sitt grundtillstånd och interagerar på ett lämpligt sätt med \(S\), och om värdet av \(A\) omedelbart före interaktionen är \(a_1\), så är \(B\):s värde omedelbart därefter \(b_1\). Om däremot \(A\):s värde omedelbart före interaktionen är \(a_2\) är \(B\):s värde därefter \(b_2\); om \(A\):s värde omedelbart före interaktionen är \(a_3\) är \(B\):s värde omedelbart därefter \(b_3\), och så vidare. Det är precis vad det betyder att säga att \(S^*\) mäter \(A\). Så om vi representerar det gemensamma, partiella tillståndet för \(S\\) och \(S^*\) (bara den del av det som specificerar värdet av , den observabel vars värden motsvarar gemensamma tilldelningar av värden till den uppmätta observabeln på \(S\) och pekarobservabeln på \(S^*\))) genom vektorn \(\ket{A=a_i}_s \ket{B=b_i}_{s^*}\), och låt ”\(\rightarrow\)” stå för den dynamiska beskrivningen av interaktionen mellan de två, att säga att \(S^*\) är ett mätinstrument för \(A\) är att säga att de dynamiska lagarna medför att,
\
och så vidare.
Intuitivt är \(S^*\) ett mätinstrument för en observerbar \(A\) bara om det finns någon observerbar egenskap hos \(S^*\) (det spelar ingen roll vad, bara något vars värden kan fastställas genom att titta på apparaten), som är korrelerad med \(A\)-värdena hos de system som matas in i apparaten på ett sådant sätt att vi kan avläsa dessa värden från \(S^*\)’s observerbara tillstånd efter interaktionen. I filosofiskt språkbruk är \(S^*\\) ett mätinstrument för \(A\), ifall det finns någon observerbar egenskap hos \(S^*\) som spårar eller indikerar \(A\)-värdena hos de system som den interagerar med på ett lämpligt sätt.
Nu följer det av (3.1) ovan att det finns tillstånd hos \(S\) (för många för att räknas) som inte är egentillstånd hos \(A\), och om vi betraktar vad Skrödingers ekvation säger oss om den gemensamma utvecklingen av \(S\) och \(S^*\) när \(S\) börjar i ett av dessa, finner vi att parets tillstånd efter interaktion är en superposition av egentillstånd hos . Det spelar ingen roll vilken observabel på \(S\) som mäts, och det spelar ingen roll vilken särskild superposition \(S\) börjar i; När den matas in i ett mätinstrument för den observabeln, om växelverkan beskrivs korrekt genom Schrödingers sekvens, följer det bara av linjäriteten hos \(U\) i den ekvationen, den operatör som åstadkommer omvandlingen från det tidigare till det senare tillståndet i paret, att det gemensamma tillståndet för \(S\) och apparaten efter växelverkan är en överlagring av egentillstånden för denna observabel på det gemensamma systemet.
Antag till exempel att vi börjar \(S^*\) i sitt grundtillstånd och \(S\) i tillståndet
Det är en följd av reglerna för att erhålla tillståndsrummet för det sammansatta systemet att parets kombinerade tillstånd är
och det följer av det faktum att \(S^*\) är ett mätinstrument för \(A\),och linjäriteten hos \(U\) att deras kombinerade tillstånd efter växelverkan är
\
Detta, dock, är oförenligt med den dynamiska regeln för sammanhang av typ 2, för den dynamiska regeln för sammanhang av typ 2 (och om det finns några sådana sammanhang är detta ett) innebär att parets tillstånd efter interaktion är antingen
\
eller
\
Indeed, innebär det att det finns en exakt sannolikhet på \(\frac{1}{2}{2}\) att det kommer att hamna i det förstnämnda fallet, och en sannolikhet på \(\frac{1}{2}{2}\) att det kommer att hamna i det sistnämnda fallet.
Vi kan försöka återställa den logiska konsekvensen genom att ge upp den dynamiska regeln för sammanhang av typ 2 (eller, vilket är samma sak, genom att förneka att det finns några sådana sammanhang), men då har vi problemet med konsekvens med erfarenheten. Vi vet hur ett system ser ut när det befinner sig i ett egentillstånd för en viss observabel, och vi vet genom att titta att mätutrustningen efter mätningen befinner sig i ett egentillstånd för pekarobservabeln. Därför vet vi redan från början att om en teori berättar något annat om mätutrustningars tillstånd efter mätningen, vad det än är för något annat, så är det fel.
Detta är i ett nötskal mätproblemet inom kvantmekaniken; alla tolkningar av teorin, alla detaljerade berättelser om hur världen ser ut enligt kvantmekaniken, och i synnerhet de delar av världen där mätningar pågår, måste ta itu med det.
Lösa ändar
Blandade tillstånd är viktade summor av rena tillstånd, och de kan användas för att representera tillstånden hos ensembler vars komponenter befinner sig i olika rena tillstånd, eller tillstånden hos enskilda system som vi bara har partiell kunskap om. I det första fallet återspeglar den vikt som är knuten till ett givet rent tillstånd storleken på den del av ensemblen som befinner sig i det tillståndet (och därmed den objektiva sannolikheten att en godtycklig medlem av ensemblen befinner sig i det tillståndet); i det andra fallet återspeglar de den epistemiska sannolikheten för att det system i fråga som tillståndet är knutet till befinner sig i det tillståndet.
Om vi inte vill förlora skillnaden mellan rena och blandade tillstånd behöver vi ett sätt att representera den viktade summan av en uppsättning rena tillstånd (motsvarande de sannolikhetsfunktioner som är förknippade med dem) som skiljer sig från att addera de (lämpligt viktade) vektorer som representerar dem, och det innebär att vi antingen behöver ett alternativt sätt att representera blandade tillstånd, eller ett enhetligt sätt att representera både rena och blandade tillstånd som bevarar skillnaden mellan dem.Det finns en typ av operatör i Hilbertrymder, en s.k. täthetsoperatör, som fungerar väl i den senare egenskapen, och det visar sig inte vara svårt att omformulera allt som sagts om tillståndsvektorer i termer av täthetsoperatörer. Så även om det är vanligt att tala som om rena tillstånd representeras av vektorer, är den officiella regeln att tillstånd – både rena och blandade – i kvantmekaniken representeras av täthetsoperatörer.
Och även om blandade tillstånd, som jag sa, kan användas för att representera vår okunskap om tillstånden hos system som faktiskt befinner sig i ett eller ett annat rent tillstånd, och även om detta har tyckts vara ett adekvat sätt att tolka blandningar i klassiska sammanhang, finns det allvarliga hinder för att tillämpa det generellt på kvantmekaniska blandningar. Dessa får diskuteras i detalj i de andra posterna om kvantmekanik i uppslagsverket.
Allt som har sagts om observabler gäller strängt taget bara för det fall där värdena för observabeln utgör en diskret mängd; de matematiska finesser som behövs för att generalisera detta till fallet med kontinuerliga observabler är komplicerade och ger upphov till problem av mer teknisk natur. Även dessa bör lämnas till en detaljerad diskussion.
Detta borde vara all den inledande förberedelse man behöver för att närma sig den filosofiska diskussionen om kvantmekanik, men det är bara ett första steg. Ju mer man lär sig om förhållandet mellan vektorer och operatörer i Hilbert-rummet, om hur enkla systemens rum förhåller sig till komplexa system och om ekvationen som beskriver hur tillståndsvektorer rör sig i rummet, desto bättre kommer man att förstå både arten och svårigheten av de problem som är förknippade med teorin. Det lustigt bakvända med kvantmekaniken, det som gör den oändligt fascinerande för en filosof, är att ju mer man lär sig, desto svårare blir problemen.