Kvanttimekaniikka
Terminologia
Fyysiset systeemit jaetaan tyyppeihin niiden muuttumattomien (tai ”tilasta riippumattomien”) ominaisuuksien mukaan, ja systeemin tila koostuu niiden ominaisuuksien täydellisestä määrittelystä, jotka muuttuvat ajan mittaan (sen ”tilasta riippuvat” ominaisuudet). Systeemin täydellisen kuvauksen antamiseksi on siis kerrottava, minkä tyyppinen systeemi se on ja mikä sen tila on kullakin hetkellä sen historiassa.
Fysikaalinen suure on toisiaan poissulkeva ja yhteisesti tyhjentävä fysikaalisten ominaisuuksien perhe (niille, jotka tuntevat tämän puhetavan, se on ominaisuuksien perhe, jolla on osion solujen rakenne). Kun tiedämme, millaisia arvoja suure ottaa, voimme tietää paljon niiden ominaisuuksien välisistä suhteista, joista se koostuu. Esimerkiksi kaksiarvoisen suureen arvot muodostavat joukon, jossa on kaksi jäsentä; reaaliarvoisen suureen arvot muodostavat joukon, jolla on reaalilukujen rakenne. Tämä on erikoistapaus asiasta, jonka tulemme näkemään yhä uudelleen, nimittäin..,että kun tiedämme, millaiset matemaattiset objektit edustavat jonkin joukon elementtejä (tässä fysikaalisen suureen arvot; myöhemmin systeemin mahdolliset tilat tai siihen liittyvät suureet), tiedämme hyvin paljon (ja luultavasti kaiken, mitä on tiedettävä) niiden välisistä suhteista.
Kvanttimekaanisissa yhteyksissä termiä ”havaittavissa oleva” käytetään vaihtelevasti ”fysikaalisen suureen” kanssa, ja sitä olisi käsiteltävä teknisenä terminä, jolla on sama merkitys. Ei ole sattumaa, että teorian varhaiset kehittäjät valitsivat tämän termin, mutta valinta tehtiin syistä, jotka eivät nykyään ole yleisesti hyväksyttyjä. Systeemin tila-avaruus on avaruus, jonka muodostaa sen mahdollisten tilojen joukko eli fysikaalisesti mahdolliset tavat yhdistää systeemiä sisäisesti luonnehtivien suureiden arvot. Klassisissa teorioissa joukko suureita, jotka muodostavat valvontaperustan muille suureille, nimetään tavallisesti ”perusjoukoksi” tai ”fundamentaalijoukoksi”, ja koska mikä tahansa matemaattisesti mahdollinen tapa yhdistää niiden arvot on fysikaalinen mahdollisuus, tilatila-avaruus saadaan yksinkertaisesti ottamalla ne koordinaateiksi. Esimerkiksi \(n\)-hiukkasista koostuvan klassisen mekaanisen systeemin tila-avaruus, joka saadaan määrittelemällä \(6n\)-reaaliarvoisten suureiden arvot – kolme sijaintikomponenttia ja kolme impulssikomponenttia jokaiselle systeemin hiukkaselle – on \(6n\)-ulotteinen koordinaattiavaruus. Tällaisen systeemin jokainen mahdollinen tila vastaa pistettä avaruudessa, ja jokainen piste avaruudessa vastaa tällaisen systeemin mahdollista tilaa. Tilanne on hieman erilainen kvanttimekaniikassa, jossa on olemassa matemaattisesti kuvattavia tapoja yhdistää sellaisten kvantiteettien arvoja, jotka eivät edusta fyysisesti mahdollisia tiloja. Kuten tulemme näkemään, kvanttimekaniikan tila-avaruudet ovat erityyppisiä vektoriavaruuksia, joita kutsutaan Hilbert-avaruuksiksi, ja niillä on enemmän sisäistä rakennetta kuin niiden klassisilla vastineilla.
Rakenne on joukko elementtejä, joille on määritelty tietyt operaatiot ja suhteet, matemaattinenrakenne on vain rakenne, jossa elementit ovat matemaattisia objekteja (lukuja, joukkoja, vektoreita) ja operaatiot matemaattisia, ja malli on matemaattinenrakenne, jota käytetään kuvaamaan jotakin fysikaalisesti merkitsevää rakennetta maailmassa.
Kvanttimekaniikan sydän ja sielu sisältyvät Hilberts-avaruuksiin, jotka edustavat kvanttimekaanisten systeemien tila-avaruuksia.Tilojen ja suureiden sisäiset suhteet ja kaikki se, mitä tämä merkitsee kvanttimekaanisten systeemien käyttäytymisestä, on kaikki kietoutunut näiden tilojen rakenteeseen, ja ne ovat ruumiillistuneet näitä tiloja edustavien matemaattisten objektien välisiin suhteisiin. Tämä tarkoittaa, että sen ymmärtäminen, millainen systeemi on kvanttimekaniikan mukaan, on erottamaton osa näiden tilojen sisäisen rakenteen tuntemusta. Kun tuntee Hilbert-avaruuden ja tutustuu dynaamisiin lakeihin, jotka kuvaavat vektoreiden kulkemia reittejä sen läpi, tietää kaiken, mitä teorian antamien ehtojen mukaan on tiedettävä systeemeistä, joita se kuvaa.
Hilbert-avaruuden tuntemisella tarkoitan jotakin muutakin kuin sen kuvauksen tai kartan hallussapitoa; kuka tahansa, jolla on hyllyssään kvanttimekaniikan oppikirja, tietää sen. Tarkoitan, että tunnet sen samalla tavalla kuin tunnet sen kaupungin, jossa asut. Tämä on käytännöllistä tietoa, joka tulee asteittain, ja se hankitaan parhaiten opettelemalla ratkaisemaan kyseiseen muotoon liittyviä ongelmia: Miten pääsen paikasta A paikkaan B? Pääsenkö sinne kulkematta C:n kautta? Entä mikä on lyhin reitti? Fysiikan jatko-opiskelijat viettävät pitkiä vuosia tutustumalla Hilberts-avaruuden nurkkiin ja kolkkiin, etsimällä tuttuja maamerkkejä, kulkemalla sen tallattuja polkuja, oppimalla, missä salakäytävät ja umpikujat sijaitsevat, ja kehittämällä käsityksen alueen yleisestä sijainnista. He oppivat navigoimaan Hilbertin avaruudessa samalla tavalla kuin taksinkuljettaja oppii navigoimaan kaupungissaan.
Miten paljon tällaista tietoa tarvitaan teoriaan liittyvien filosofisten ongelmien lähestymiseksi? Aluksi ei kovin paljon: vain yleisimmät tosiasiat maiseman geometriasta (joka on joka tapauksessa, toisin kuin useimmat kaupungit, kauniisti järjestetty) ja poluista, joita (systeemien tiloja edustavat vektorit) kulkevat niiden läpi. Tämä on se, mitä tässä esitellään: ensin hiukan helppoa matematiikkaa ja sitten pähkinänkuoressa teoriaa.
Matematiikka
2.1 Vektorit ja vektoriavaruudet
Vektori \(A\), joka kirjoitetaan ’\(\ket{A}\)’, on matemaattinen objekti, jolle on ominaista pituus, \(|A|\), ja suunta. Anormalisoitu vektori on vektori, jonka pituus on 1, eli \(|A| = 1\). Vektorit voidaan laskea yhteen, kertoa vakioilla (myös kompleksiluvuilla) ja kertoa keskenään. Vektorien yhteenlasku kuvaa minkä tahansa vektoriparin toiseen vektoriin, tarkemmin sanottuna toiseen vektoriin, joka saadaan siirtämällä toista vektoria niin, että sen pyrstö osuu ensimmäisen vektorin kärkeen muuttamatta kummankaan vektorin pituutta tai suuntaa, ja liittämällä sitten ensimmäisen vektorin pyrstö toisen vektorin kärkeen. Tämä yhteenlaskusääntö tunnetaan nimellä parallelogrammilaki. Esimerkiksi vektoreiden \(\ket{A}\) ja \(\ket{B}\) yhteenlasku antaa vektorin \(\ket{C}). (= \ket{A} + \ket{B})\) kuten kuvassa 1:
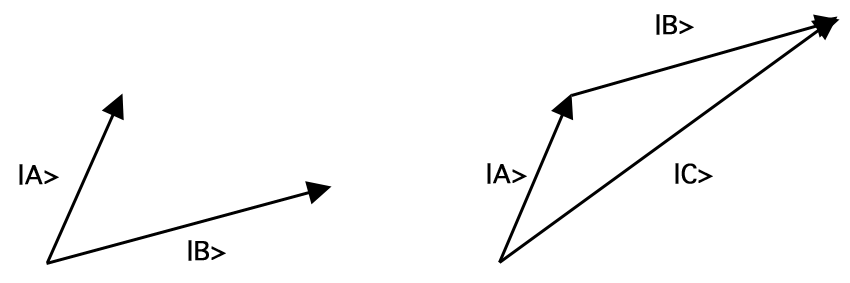
Kuva 1. Vektorien yhteenlasku.Vektorien yhteenlasku
Kertomalla vektori \(\ket{A}\) luvulla \(n\), jossa \(n\) on vakio, saadaan vektori, joka on samansuuntainen kuin \(\ket{A}\) mutta jonka pituus on \(n\) kertaa \(\ket{A}\):n pituus.
Reaalisessa vektoriavaruudessa vektoriparin \(\ket{A}\) ja \(\ket{B}\) (sisä- tai pistetuotto), kirjoitettuna’\(\braket{A}{B}\)’, on skalaari, joka on yhtä suuri kuin niiden pituuksien (tai ’normien’) tulo kerrottuna niiden välisen kulman kosinuksella \(\(\theta\)):
\\
Olkoot \(\ket{A_1}\) ja \(\ket{A_2}\) vektorit, joiden pituus on 1(”yksikkövektorit”) siten, että \(\braket{A_1}{A_2} = 0\). (Näiden kahden yksikkövektorin välisen kulman on oltava 90 astetta.) Tällöin voimme esittää minkä tahansa kaksiulotteisen vektorin \(\ket{B}\) yksikkövektoriemme avulla seuraavasti:
\
Tässä on esimerkiksi kuvaaja, joka osoittaa, miten \(\ket{B}\) voidaan esittää kahden yksikkövektorin \(\ket{A_1}\) ja \(\ket{A_2}\) summana:
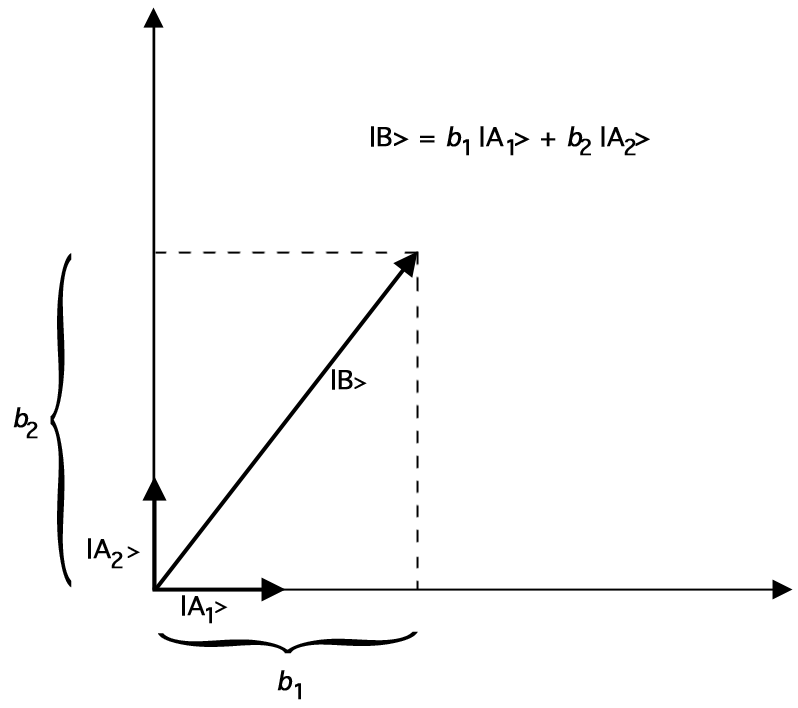
Kuvio 2. \(\ket{B}\) esittäminen yksikkövektoreiden vektorilisäyksellä
Nyt sisäisen tuotteen \(\braket{A}{B}\) määritelmää on muutettava, jotta sitä voidaan soveltaa kompleksiavaruuksiin. Olkoon \(c^*\) \(c\):n kompleksikonjugaatti. (Kun \(c\) on kompleksiluku muodossa \(a \pm bi\), niin \(c\):n kompleksikonjugaatti\(c^*\) määritellään seuraavasti:
\^* = a-bi \\\^* = a+bi\]
Siten kaikille kompleksiluvuille \(c\), \(^* = c\),mutta \(c^* = c\) vain siinä tapauksessa, että \(c\) on reaalinen). Nyt \(\ket{A}\) ja \(\ket{B}\) sisäisen tuotteen määritelmä kompleksiavaruuksille voidaan antaa kompleksikertoimien konjugaattien avulla seuraavasti. Jossa \(\ket{A_1}\) ja \(\ket{A_2}\) ovat aiemmin kuvatut yksikkövektorit, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}\) ja \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}\), silloin
\\
Sisätuotteen yleisin ja abstraktimpi käsite, josta olemme nyt määritelleet kaksi erikoistapausta, on seuraava. \(\braket{A}{B}\) on sisäinen tuote vektoriavaruudessa \(V\) juuri siinä tapauksessa, että
- \(\braket{A}{A} = |A|^2\), ja \(\braket{A}{A}=0\) jos ja vain jos \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}^*\)
- \(\braket{B}{A+C}=\braket{B}{A} + \braket{B}{C}\).
Tästä seuraa, että
- pituus \(\ket{A}\) on neliöjuuri \(\ket{A}\):n sisätuotosta itsensä kanssa, ts,\
ja
- \(\ket{A}\) ja \(\ket{B}\) ovat toisiinsa nähden kohtisuorassa eli kohtisuorassa, jos ja vain jos \(\braket{A}{B}\).
Vektoriavaruus on vektoreiden joukko, joka on suljettu yhteenlaskun ja vakioilla kertomisen suhteen, sisäinen tuotosavaruus on vektoriavaruus, jolle on määritelty vektoreiden kertomisen operaatio, ja tällaisen avaruuden ulottuvuus on sen sisältämien nollasta poikkeavien, toisiinsa nähden kohtisuorassa olevien vektoreiden enimmäismäärä.
Jokainen \(N\)-ulotteisen vektoriavaruuden \(N\)-ulotteisten \(N\)-ulotteisten \(N\)-ulotteisten, keskenään ortonormaalien, pituudeltaan 1:n pituisten vektoreiden kokoelma muodostaa ortonormaalipohjan kyseiselle avaruudelle. Olkoon \(\ket{A_1}, \ldots, \ket{A_N}\) tällainen yksikkövektorien kokoelma. Tällöin jokainen avaruuden vektori voidaan ilmaista summana muodossa:
\\
jossa \(b_i = \braket{B}{A_i}\). \(b_i\):t tunnetaan tässä \(B\):n laajenemiskertoimina \(A\)-perustassa.
Huomaa, että:
- kaikille vektoreille \(A\), \(B\) ja \(C\) tietyssä avaruudessa,\
- kaikille vektoreille \(M\) ja \(Q\) ilmaistuna \(A\)-perustassa,\
ja
\
On toinenkin tapa kirjoittaa vektorit, nimittäin kirjoittamalla laajennuskertoimet (suhteessa tiettyyn perustaan) sarakkeeseen, kuten esim: \(q_i = \braket{Q}{A_i}\) ja \(A_i\) ovat valitut perusvektorit.
Kun käsittelemme äärettömän mittaisia vektoriavaruuksia, koska emme voi kirjoittaa koko paisuntakertoimien saraketta, jota tarvitaan vektorin poimimiseen, koska sen pitäisi olla äärettömän pitkä, joten sen sijaan kirjoitamme ylös funktion (jota kutsutaan aaltofunktioksi \(Q\), joka yleensä esitetään muodossa \(\psi(i))\), jolla on nämä kertoimet arvoina. Kirjoitamme ylös siis funktion:
\\
Jos meillä on mikä tahansa vektori ja mikä tahansa perusta vektoriavaruudessa, voimme saada vektorin aaltofunktion kyseisessä perustassa; ja jos meillä on vektorin aaltofunktio tietyssä perustassa, voimme rakentaa vektorin, jonka aaltofunktio se on. Koska käy ilmi, että useimmat tärkeät operaatiot vektoreille vastaavat yksinkertaisia algebrallisia operaatioita niiden aaltofunktioille, tämä on tavallinen tapa esittää tilavektorit.
Kun pari fysikaalista systeemiä on vuorovaikutuksessa keskenään, ne muodostavat yhdistetyn systeemin, ja niin kvanttimekaniikassa kuin klassisessa mekaniikassakin on olemassa sääntö, jonka mukaan yhdistetyn systeemin tilatila-avaruus muodostetaan sen komponenttien tilatiloista, Sääntö, joka kertoo, miten tilatiloista \(H_A\) ja \(H_B\) saadaan \(A\):n ja \(B\):n tilatiloista parin tilatila, jota kutsutaan \(H_A\):n ja \(H_B\):n ”tensorituotteeksi” ja joka on kirjoitettu \(H_A \ kertaa H_B\). Sääntöön liittyy kaksi tärkeää asiaa: ensinnäkin niin kauan kuin \(H_A\) ja \(H_B\) ovat Hilbert-avaruuksia, myös \(H_A \ kertaa H_B\) on sellainen, ja toiseksi on olemassa joitakin tosiasioita, jotka koskevat tapaa, jolla \(H_A \ kertaa H_B\) liittyy \(H_A\) ja \(H_B\), ja joilla on yllättäviä seurauksia kompleksisen systeemin ja sen osien välisille suhteille. Erityisesti käy ilmi, että komposiittijärjestelmän tila ei ole yksiselitteisesti määritelty sen osien tilan perusteella. Tämä tarkoittaa, tai ainakin vaikuttaa siltä, että kvanttimekaniikan mukaan on olemassa komposiittisysteemejä koskevia tosiasioita (eikä vain niiden tilakokoonpanoa koskevia tosiasioita), jotka eivät ole riippuvaisia niiden osia koskevista tosiasioista; se tarkoittaa, että on olemassa systeemejä kokonaisuuksina koskevia tosiasioita, jotka eivät ole riippuvaisia tosiasioista, jotka koskevat niiden osia ja tapaa, jolla nuo osat on järjestetty avaruudessa. Tämän teorian ominaisuuden merkitystä ei voi vähätellä; se liittyy tavalla tai toisella useimpiin teorian vaikeimpiin ongelmiin.
Hieman yksityiskohtaisemmin: Jos \(\(\{v_{i}^A\}\) on ortonormaali perusta \(H_A\):lle ja \(\(\{u_{j}^B\}\) on ortonormaali perusta \(H_B\):lle, parien \((v_{i}^A, u_{j}^B)\)\) joukon katsotaan muodostavan ortonormaalin perustan tensorituotantoavaruudelle \(H_A \times H_B\). Parista \((v_{i}^A,u_{j}^B)\) käytetään merkintää \(v_{i}^A,u_{j}^B)\), ja sisäinen tuote \(H_A \ kertaa H_B\) määritellään seuraavasti:
\
Konstruktiosta seuraa, että vaikka jokainen vektori \(H_A \ kertaa H_B\) on lineaarinen summa vektoreista, jotka ovat ilmaistavissa muodossa \(v^A \ kertaa u^B\), eivät kaikki avaruuden vektorit ole itse ilmaistavissa kyseisessä muodossa, ja käy ilmi, että
- yhdistelmätila määrittelee yksikäsitteisesti komponenttiensa tilat.
- jos \(A\) ja \(B\) tilat ovat puhtaita (ts, edustettavissa vektoreilla \(v^A\) ja \(u^B\)), silloin \((A+B)\) tila on puhdas ja sitä edustaa\(v^A \ kertaa u^B\), ja
- jos \((A+B)\):n tila on puhdas ja ilmaistavissa muodossa \(v^A \ kertaa u^B\), niin \(A\):n ja \(B\):n tilat ovat puhtaita, mutta
- jos \(A\):n tilat eivät ole puhtaita, i.e., jos ne ovat sekatiloja (nämä määritellään jäljempänä), ne eivät yksiselitteisesti määrittele tilaa \((A+B)\); erityisesti se voi olla puhdas tila, jota ei voida ilmaista muodossa \(v^A \ kertaa u^B\).
2.2 Operaattorit
Operaattori \(O\) on vektoriavaruuden kuvaaminen itseensä; se vie minkä tahansa vektorin \(\ket{B}\) avaruudessa toiseen vektoriin \(\ket{B’}\), joka on myös avaruudessa; \(O \ket{B} = \ket{B’}\). Lineaariset operaattorit ovat operaattoreita, joilla on seuraavat ominaisuudet:
- \(O(\ket{A} + \ket{B}) = O \ket{A}). + O \ket{B}\), ja
- \(O(c \ket{A}) = c(O \ket{A})\).
Aivan kuten mikä tahansa vektori \(N\)-ulotteisessa avaruudessa voidaan esittää \(N\)-lukujen sarakkeella, suhteutettuna valittuun avaruuden perustaan, mikä tahansa lineaarinen operaattori voidaan esittää sarakkeellisessa merkintätapauksessa \(N ^2\)-lukujen avulla:
\
jossa \(O_{ij} = \braket{A_i}{O \mid A_j}\) ja \(A_N\) ovat avaruuden perusvektorit. Lineaarisen operaattorin \(O\) vaikutus vektoriin\(B\) on siis
\
Kaksi määritelmää vielä ennen kuin voimme sanoa, mitä Hilbert-avaruudet ovat, ja sitten voimme siirtyä kvanttimekaniikkaan. \(\ket{B}\) on \(O\):n ominaisvektori, jonka ominaisarvo on \(a\), jos ja vain jos \(O \ket{B} = a \ket{B}\).Eri operaattoreilla voi olla erilaisia ominaisvektoreita, mutta ominaisvektorin ja operaattorin suhde riippuu vain kyseisestä operaattorista ja vektoreista eikä siitä, millä perusteella ne on ilmaistu; ominaisvektorin ja operaattorin suhde on toisin sanoen muuttumaton perustan vaihtuessa. Hermite-operaattori on operaattori, jolla on se ominaisuus, että on olemassa ortonormaali perusta, joka koostuu sen ominaisvektoreista, ja että nämä ominaisarvot ovat kaikki todellisia.
Hilbertin avaruus on vektoriavaruus, jolle on määritelty sisäinen tulo ja joka on täydellinen eli sellainen, että mikä tahansa avaruuden vektoreiden Cauchy-sarja konvergoi avaruuden vektoriin. Kaikki äärellisulotteiset sisäisen tuotteen tilat ovat täydellisiä, ja rajoitun näihin. Äärettömään tapaukseen liittyy joitakin komplikaatioita, joihin ei tässä vaiheessa ole hedelmällistä puuttua.
Kvanttimekaniikka
Kvanttimekaniikan neljä perusperiaatetta ovat:
(3.1)
Fysikaaliset tilat.Jokaiseen fysikaaliseen systeemiin liittyy Hilbert-avaruus, jonka jokainen yksikkövektori vastaa systeemin mahdollista puhdasta tilaa ja jokainen mahdollinen puhdas tila jotakin avaruuden vektoria.
(3.2)
Fysikaaliset suureet.Systeemiin liittyvässä Hilbert-avaruudessa esiintyvät hermeettiset operaattorit edustavat fysikaalisia suureita, ja niiden ominaissuureet edustavat mahdollisten mittausten tuloksia noista suureista.
On olemassa operaattori, jota kutsutaan Hamiltonianiksi, jolla on erityinen rooli kvanttiteoriassa, koska systeemin dynamiikka voidaan muotoilla kätevästi seuraamalla sen kehitystä. Hamiltonian – kirjoitettuna \(H\) tai \(\hat{H}\) – tarkoittaa systeemin kokonaisenergiaa. Sen ominaisarvot ovat mahdollisia tuloksia, jotka voidaan saada kokonaisenergian mittauksissa. Se saadaan laskemalla yhteen systeemin komponenttien kineettiset ja potentiaalienergiat.
(3.3)
Kompositio.Monimutkaiseen systeemiin liittyvä Hilbert-avaruus on niiden yksinkertaisten systeemien (standardissa, ei-relativistisessa teoriassa: yksittäisten hiukkasten), joista systeemi koostuu, Hilbert-avaruuden tensoritulos.
(3.4) Dynamiikka. a.
Tyypin 1 kontekstit: Kun systeemin tila hetkellä \(t\) ja siihen kohdistuvat voimat ja rajoitukset ovat tiedossa, on olemassa yhtälö, ”Schrödingerin sekvenssi”, joka antaa tilan millä tahansa muulla ajanhetkellä \(\(U\ket{v_t} \rightarrow \ket{v_{t’}}\). Tarkoituksemme kannalta \(U\):n tärkeät ominaisuudet ovat, että se on deterministinen eli se muuttaa systeemin yhden ajanhetken tilan yksikäsitteiseksi toisen ajanhetken tilaksi, se on unitaarinen eli se on sen Hilbert-avaruuden automorfismi, johon se vaikuttaa (ts, se on lineaarinen, eli jos se vie tilan \(\ket{A}\) tilaan\(\ket{A’}\), se on lineaarinen,) ja se ottaa tilan \(\ket{B}\) tilaan\(\ket{B’}\), niin se ottaa minkä tahansa tilan muodossa \(\alpha \ket{A} +\beta \ket{B}\) tilaan \(\alpha \ket{A’} + \beta\ket{B’}\).
b.
Tyypin 2 kontekstit (”Mittauskontekstit”): Havaittavan \(B\) ”mittauksen” suorittaminen systeemille, joka on tilassa \(\ket{A}\), vaikuttaa siten, että systeemi luhistuu havaittua ominaistilaa vastaavaan \(B\)-ominaisarvotilaan. Tämä tunnetaan nimellä CollapsePostulate. Se, mihin tiettyyn \(B\)-eigeenitilaan se luhistuu, on todennäköisyyskysymys, ja todennäköisyydet annetaan Bornin säännön avulla:
\
Näistä kahdesta kontekstityypistä on huomioitava kaksi tärkeää seikkaa:
- Tyypin 1 ja 2 kontekstien välinen ero on kvanttimekaanisesti vielä selvittämättä; kukaan ei ole onnistunut sanomaan täysin tyydyttävällä tavalla teorian tarjoamilla termeillä, mitkä kontekstit ovat mittauskonteksteja, ja
- Jopa jos ero on selvillä, on tulkinnallisesti avoin kysymys, onko olemassa tyypin 2 konteksteja; i.e., on avoin tulkinnallinen kysymys, onko olemassa konteksteja, joissajärjestelmiä hallitsee jokin muu dynaaminen sääntö kuin Schrödingerin yhtälö.
Rakenteet Hilbert-avaruudessa
Huomautin edellä, että samalla tavalla kuin kaikki tieto, jota meillä on kaupungin paikkojen välisistä suhteista, sisältyy niitä esittävien karttapisteiden välisiin paikkasuhteisiin, kaikki tieto, jota meillä on kvanttimekaniikan tilojen ja suureiden välisistä (ja niiden välisistä) sisäisistä suhteista, sisältyy niitä esittävien vektoreiden ja operaattoreiden välisiin matemaattisiin suhteisiin. Matemaattisesta näkökulmasta kvanttimekaniikka eroaa klassisista edeltäjistään siinä, että tilat ja suureet ovat rakenteeltaan rikkaampia; ne muodostavat perheitä, joiden jäsenten välillä on mielenkiintoisempi suhteiden verkosto.
Kvanttimekaanisten systeemien käyttäytymisen kaikki fysikaalisesti merkittävät piirteet ovat seurauksia näiden suhteiden matemaattisista ominaisuuksista, ja tärkeimmät niistä ovat helposti tiivistettävissä:
(P1)
Millä tahansa tavalla laskemalla yhteen vektoreita Hilbert-avaruudessa tai kertomalla niitä skalaareilla saadaan vektori, joka on myös kyseisessä avaruudessa. Jos vektori on normalisoitu, se edustaa (3.1) perusteella systeemin mahdollista tilaa, ja jos se on havaittavissa olevan \(B\) ominaisvektoriparin summa, jolla on erilaiset ominaisarvot, se ei itsessään ole \(B\):n ominaisvektori, vaan siihen liittyy (3.4b) perusteella joukko todennäköisyyksiä, joilla voidaan näyttää yhtä tai toista tulosta \(B\)-mittauksissa.
(P2)
Mille tahansa Hilbert-avaruuden hermeettiselle operaattorille on olemassa muita, samassa avaruudessa olevia operaattoreita, joiden kanssa se ei jaa täyttä omakohtaisten vektoreiden joukkoa; itse asiassa on helppo osoittaa, että on olemassa muita sellaisia operaattoreita, joiden kanssa sillä ei ole yhtään yhteistä omakohtaista vektoria.
Jos teemme pari ylimääräistä tulkintaoletusta, voimme sanoa enemmän. Oletetaan esimerkiksi, että
(4.1)
Jokainen systeemiin assosioituvan Hilbert-avaruuden hermeettinen operaattori edustaa erillistä havaintokohtaa ja (siten)jokainen normalisoitu vektori erillistä tilaa, ja
(4.2)
Systeemillä on arvo havaintokohteelle \(A\), jos ja vain jos sen tilaa edustava vektori on ominaistilanne operaattorille \(A\). Arvo, joka sillä on tällaisessa tapauksessa, on vain kyseiseen ominaistilaan liittyvä ominaisarvo.
Kohdasta (P2) seuraa (3.1), että mikään kvanttimekaaninen tila ei ole kaikkien havaintomuuttujien ominaistila (ja itse asiassa on olemassa havaintomuuttujia, joilla ei ole yhteisiä ominaistiloja), ja näin ollen (3.2) kohdan (2.1) mukaisesti.2), että millään kvanttimekaanisella systeemillä ei koskaan ole samanaikaisia arvoja kaikille siihen kuuluville suureille (ja että on olemassa sellaisia suurepareita, joille mikään tila ei anna samanaikaisia arvoja).
On olemassa hermeettisiä operaattoreita parin Hilbert-avaruuden tensorituotteelle \(H_1 \ kertaa H_2\) \(H_1\) ja \(H_2\) … Jos \(H_1\) ja\(H_2\) ovat järjestelmien \(S1\) ja \(S2\) tilaavaruuksia,\(H_1 \ kertaa H_2\) on kompleksisen järjestelmän \((S1+S2)\) tilaavaruus. Tästä seuraa (4.1) avulla, että on olemassa \((S1+S2)\):iin kuuluvia havaintomuuttujia, joiden arvot eivät määräydy kahteen erilliseen \((S1+S2)\):iin kuuluvien havaintomuuttujien arvojen perusteella.
Nämä kaikki ovat suoraviivaisia seurauksia siitä, että Hilbertin avaruuden vektoreiden ja operaattoreiden otetaan edustamaan tiloja ja havaintomuuttujia, ja että tilojen osoittamiselle annetaan empiirinen merkitys soveltamalla Bornin sääntöä (ja myöhempiä kohtia (4.1) ja (4.2)). Kvanttimekaniikan ymmärtämisen todellinen vaikeus on sen fyysisten, metafyysisten ja epistemologisten implikaatioiden ymmärtämisessä.
Jokainen, joka yrittää ymmärtää, mitä kvanttimekaniikka kertoo maailmasta, joutuu kamppailemaan yhden jäljellä olevan tosiasian kanssa. Tämä ongelma ei liity Hilbert-avaruuteen, vaan dynamiikkaan – sääntöihin, jotka kuvaavat systeemien kulkureittejä avaruuden läpi. Fysikaalisesta näkökulmasta se on paljon huolestuttavampi kuin mikään tähän mennessä käsitelty. Se ei ainoastaan aiheuta vaikeuksia jollekin, joka yrittää tarjota teorian tulkintaa, vaan näyttää myös viittaavan loogiseen epäjohdonmukaisuuteen teorian perusteissa.
Oletetaan, että meillä on systeemi \(S\) ja laite \(S^*\), joka mittaa havaittavaa \(A\) \(S\) \(S\):ssä, jonka arvot ovat \(\(\{a_1,a_2,a_2, a_3, …\\}\). Sitten on olemassa jokin \(S^*\) tila (”perustila”) ja jokin havaintomuuttuja \(B\), jonka arvot ovat \(\(\{b_1, b_2,b_3, …\}\), joka liittyy \(S^*\):iin (sen ”osoitinhavaittavuus”, jota kutsutaan niin, koska se on se, joka toimii osoittimena skemaattisen mittauslaitteen etupuolella olevan asteikon osoittimessa, joka rekisteröi kokeen tuloksen), jotka ovat sellaisia, että jos \(S^*\) käynnistetään perustilassaan ja vuorovaikutetaan sopivalla tavalla \(S\):n kanssa ja jos \(A\):n arvo välittömästi ennen vuorovaikutusta on \(a_1\), niin \(B\):n arvo välittömästi vuorovaikutuksen jälkeen on \(b_1\). Jos taas \(A\):n arvo välittömästi ennen vuorovaikutusta on \(a_2\), \(B\):n arvo välittömästi sen jälkeen on \(b_2\); jos \(A\):n arvo välittömästi ennen vuorovaikutusta on \(a_3\), \(B\):n arvo välittömästi sen jälkeen on \(b_3\) jne. Juuri tätä tarkoittaa, että \(S^*\) mittaa \(A\). Jos siis esitämme \(S\):n ja \(S^*\):n yhteisen, osittaisen tilan (vain sen osan, joka määrittelee sen havaintokohteen arvon, jonka arvot vastaavat mitatun havaintokohteen \(S\):n ja osoitinhavaintokohteen \(S^*\):n yhteisiä arvoja) vektorilla\(\ket{A=a_i}_s \ket{B=b_i}_{s^*}\), ja ”\(\rightarrow\) ”edustaa näiden kahden välisen vuorovaikutuksen dynaamista kuvausta, ja jos sanotaan, että \(S^*\) on \(A\):n mittauslaite, on sanottava, että dynaamiset lait johtavat siihen,
\
ja niin edelleen.
Intuitiivisesti \(S^*\) on mittauslaite havaittavalle \(A\):lle vain siinä tapauksessa, että \(S^*\):lla on jokin havaittava ominaisuus (ei ole väliä mikä, kunhan vain jokin, jonka arvot voidaan todeta katsomalla laitetta), joka korreloi siihen syötettävien systeemien \(A\)-arvojen kanssa siten, että voimme lukea nuo arvot vuorovaikutussuhteen päätyttyä havaittavasta \(A \):n tilasta. Filosofisessa kielenkäytössä \(S^*\) on \(A\):n mittausväline vain siinä tapauksessa, että \(S^*\):llä on jokin havaittavissa oleva ominaisuus, joka seuraa tai osoittaa niiden järjestelmien \(A\)-arvoja, joiden kanssa se on vuorovaikutuksessa sopivalla tavalla.
Yllä olevasta kohdasta (3.1) seuraa, että \(S\):llä on tiloja (liian monta laskettavaksi), jotka eivät ole \(A\):n ominaistiloja, ja jos tarkastelemme sitä, mitä Schrödingerin yhtälö kertoo meille \(S\):n ja \(S^*\):n yhteisestä kehityksestä silloin, kun \(S\) aloitetaan jommassa kummassa, huomaamme, että vuorovaikutuksen jälkeinen parin tila on \(S^*\):n ja \(S^*\):n \(S^*\):n \(S^*\):n \(S^*\):n \(S^*\):n \(S^*\):n \(S^*\):n ^(S^*\):n ominaistilojen superpositio. Ei ole väliä, mitä havaintoa \(S\):stä mitataan, eikä sillä ole väliä, mistä superpositiosta \(S\) lähtee liikkeelle; jos vuorovaikutus kuvataan oikein Schrödingerin yhtälöllä, seuraa pelkästään yhtälön \(U\) lineaarisuudesta, operaattorin, joka saa aikaan muunnoksen parin aikaisemmasta tilasta myöhempään tilaan, että vuorovaikutuksen jälkeinen \(S\):n ja laitteen yhteinen tila on tämän havaittavan ominaisuustilojen superpositio yhteisessä systeemissä, kun se syötetään kyseisen havaittavan ominaistiloihin.
Asettakaamme esimerkiksi, että aloitamme \(S^*\):n perustilassaan ja \(S\):n tilassa
\
Se on seurausta yhdistetyn systeemin tilaavaruuden saamista koskevista säännöistä, että parin yhdistetty tila on
\
, ja se seuraa siitä, että \(S^*\) on mittauslaite \(A\):lle,ja \(U\) lineaarisuudesta, että niiden yhteenlaskettu tila vuorovaikutuksen jälkeen on
\
Tämä kuitenkin, on ristiriidassa tyypin 2 konteksteja koskevan dynaamisen säännön kanssa, sillä tyypin 2 konteksteja koskeva dynaaminen sääntö (ja jos tällaisia konteksteja on olemassa, tämä on yksi niistä) edellyttää, että parin tila vuorovaikutuksen jälkeen on joko
\
tai
\
Todellakin, se merkitsee, että on olemassa tarkka todennäköisyys \(\frac{1}{2}\), että se päätyy ensimmäiseen, ja todennäköisyys \(\frac{1}{2}\), että se päätyy jälkimmäiseen.
Voidaan yrittää palauttaa looginen johdonmukaisuus luopumalla tyypin 2 konteksteja koskevasta dynaamisesta säännöstä (tai, mikä on sama asia, kieltämällä, että tällaisia konteksteja on olemassa), mutta silloin meillä on ongelma johdonmukaisuudesta kokemuksen kanssa. Kyseisen säännön sisällyttäminen teoriaan ei nimittäin ollut pelkkä kömmähdys; tiedämme, miltä systeemi näyttää, kun se on tietyn havaittavissa olevan ominaisuustilassa, ja tiedämme silmämääräisesti, että mittauslaite on mittauksen jälkeen osoittimen havaittavissa olevan ominaisuustilassa. Ja niinpä tiedämme alusta alkaen, että jos teoria kertoo meille jotain muuta mittauslaitteiden mittauksen jälkeisistä tiloista, olipa se sitten mitä tahansa, se on väärin.
Tämä on pähkinänkuoressa kvanttimekaniikan mittausongelma; mikä tahansa teorian tulkinta, mikä tahansa yksityiskohtainen kertomus siitä, millainen maailma on kvanttimekaniikan mukaan, ja erityisesti ne maailman osat, joissa mittauksia tehdään, joutuu kamppailemaan sen kanssa.
Loose Ends
Sekatilat ovat puhtaiden tilojen painotettuja summia, ja niitä voidaan käyttää kuvaamaan sellaisten kokonaisuuksien tiloja, joiden osat ovat erilaisissa puhtaissa tiloissa, tai sellaisten yksittäisten järjestelmien tiloja, joista meillä on vain osittaista tietoa. Ensimmäisessä tapauksessa tiettyyn puhtaaseen tilaan liitetty paino kuvastaa sen kokonaisuuden osan kokoa, joka on kyseisessä tilassa (ja siten objektiivista todennäköisyyttä, että kokonaisuuden mielivaltainen jäsen on kyseisessä tilassa); toisessa tapauksessa ne kuvastavat episteemistä todennäköisyyttä, että kyseinen järjestelmä, johon tila on liitetty, on kyseisessä tilassa.
Jos emme halua menettää eroa puhtaiden ja sekatilojen välillä, tarvitsemme tavan esittää puhtaiden tilojen joukon (vastaavasti niihin liittyvien todennäköisyysfunktioiden) painotettu summa, joka on erilainen kuin niitä edustavien (sopivasti painotettujen) vektorien yhteenlaskeminen, ja tämä tarkoittaa, että tarvitsemme joko vaihtoehtoisen tavan esittää sekatiloja tai yhdenmukaisen tavan esittää sekä puhtaita että sekatiloja siten, että niiden välinen ero säilyy.Hilbert-avaruuksissa on eräänlainen operaattori, jota kutsutaan tiheysoperaattoriksi ja joka soveltuu hyvin jälkimmäiseen tarkoitukseen, eikä osoittautuukaan vaikeaksi muotoilla kaikkea sitä, mitä on sanottu tilavektoreista, uudelleen tiheysoperaattoreiden avulla. Vaikka tavallisesti puhutaankin niin, että puhtaat tilat esitetään vektoreilla, virallinen sääntö on, että tilat – sekä puhtaat että sekatilat – esitetään kvanttimekaniikassa tiheysoperaattoreilla.
Vaikka sekatiloja voidaan, kuten sanoin, käyttää kuvaamaan tietämättömyyttämme sellaisten systeemien tiloista, jotka ovat todellisuudessa yhdessä tai toisessa puhtaassa tilassa, ja vaikka tämä on monista tuntunut riittävältä tavalta tulkita sekatiloja klassisissa yhteyksissä, on vakavia esteitä soveltaa sitä yleisesti kvanttimekaanisiin sekatiloihin. Niitä käsitellään yksityiskohtaisesti muissa tietosanakirjan kvanttimekaniikkaa koskevissa kohdissa.
Kaikki se, mitä on sanottu havaintomuuttujista, pätee tarkalleen ottaen vain tapaukseen, jossa havaintomuuttujan arvot muodostavat diskreetin joukon; matemaattiset hienoudet, joita tarvitaan sen yleistämiseksi jatkuvien havaintomuuttujien tapaukseen, ovat monimutkaisia, ja ne aiheuttavat teknisempiä ongelmia. Nämäkin on parasta jättää yksityiskohtaisen keskustelun varaan.
Tämän pitäisi olla kaikki alkuvalmistelut, joita tarvitaan lähestyttäessä filosofista keskustelua kvanttimekaniikasta, mutta se on vain ensimmäinen askel. Mitä enemmän oppii vektoreiden ja operaattoreiden välisistä ja niiden välisistä suhteista Hilbert-avaruudessa, siitä, miten yksinkertaisten systeemien tilat liittyvät monimutkaisten systeemien tiloihin, ja yhtälöstä, joka kuvaa tilavektoreiden liikkumista avaruudessa, sitä paremmin ymmärtää teoriaan liittyvien ongelmien luonteen ja vaikeuden. Kvanttimekaniikassa on se hassu takaperoinen piirre, joka tekee siitä filosofin kannalta loputtoman kiehtovan, että mitä enemmän oppii, sitä vaikeammiksi ongelmat muuttuvat.