Quantum Mechanica
Terminologie
Fysische systemen worden in typen verdeeld naar hun onveranderlijke (of ’toestandsafhankelijke’) eigenschappen, en de toestand van een systeem op een bepaald moment bestaat uit een volledige specificatie van die eigenschappen die met de tijd veranderen (zijn ’toestandsafhankelijke’ eigenschappen). Om een complete beschrijving van een systeem te geven, moeten we dus zeggen welk type systeem het is en wat de toestand ervan is op elk moment in zijn geschiedenis.
Een fysische grootheid is een wederzijds uitsluitende en gezamenlijk uitputtende familie van fysische eigenschappen (voor degenen die deze manier van praten kennen, het is een familie van eigenschappen met de structuur van de cellen in een partitie). Weten welke waarden een grootheid heeft, kan ons veel vertellen over de relaties tussen de eigenschappen waaruit zij is samengesteld. De waarden van een bivalente grootheid bijvoorbeeld vormen een verzameling met twee leden; de waarden van een reële grootheid vormen een verzameling met de structuur van de reële getallen. Dit is een speciaal geval van iets dat we steeds weer zullen zien, namelijk..,dat weten wat voor soort wiskundige objecten de elementen in een of andere verzameling vertegenwoordigen (hier de waarden van een fysische grootheid; later de toestanden die een systeem kan aannemen, of de grootheden die erbij horen) ons heel veel vertelt (inderdaad, aantoonbaar, alles wat er te weten valt) over de onderlinge relaties.
In kwantummechanische contexten wordt de term ‘waarneembaar’ door elkaar gebruikt met ‘fysische grootheid’, en moet hij behandeld worden als een technische term met dezelfde betekenis. Het is geen toeval dat de vroege ontwikkelaars van de theorie voor deze term kozen, maar de keuze werd gemaakt om redenen die tegenwoordig niet meer algemeen aanvaard zijn. De toestandsruimte van een systeem is de ruimte die wordt gevormd door de verzameling van zijn mogelijke toestanden, d.w.z. de fysisch mogelijke manieren om de waarden van de grootheden die het systeem intern karakteriseren, te combineren. In klassieke theorieën wordt een reeks grootheden die een superveniencebasis vormt voor de rest, gewoonlijk aangeduid als “fundamenteel” of “fundamenteel”, en aangezien elke wiskundig mogelijke manier om hun waarden te combineren een fysische mogelijkheid is, kan de toestandsruimte worden verkregen door deze eenvoudigweg als coördinaten te nemen. Zo is bijvoorbeeld de toestandsruimte van een klassiek mechanisch systeem dat bestaat uit een aantal deeltjes en dat wordt verkregen door de waarden van drie reële grootheden – drie positiecomponenten en drie impulscomponenten voor elk deeltje in het systeem – op te geven, een coördinatenruimte met zes dimensies. Elke mogelijke toestand van zo’n systeem komt overeen met een punt in de ruimte, en elk punt in de ruimte komt overeen met een mogelijke toestand van zo’n systeem. De situatie is een beetje anders in de kwantummechanica, waar er wiskundig beschrijfbare manieren zijn om de waarden van de grootheden te combineren die geen fysisch mogelijke toestanden vertegenwoordigen. Zoals we zullen zien, zijn de toestandsruimten van de kwantummechanica speciale soorten vectorruimten, die Hilbert-ruimten worden genoemd, en ze hebben meer interne structuur dan hun klassieke tegenhangers.
Een structuur is een verzameling elementen waarop bepaalde operaties en relaties gedefinieerd zijn, een wiskundige structuur is gewoon een structuur waarin de elementen wiskundige objecten zijn (getallen, verzamelingen, vectoren) en de operaties wiskundige, en een model is een wiskundige structuur die gebruikt wordt om een of andere fysisch significante structuur in de wereld weer te geven.
Het hart en de ziel van de kwantummechanica ligt besloten in de Hilbertruimten die de toestandsruimten van kwantummechanische systemen weergeven. De interne relaties tussen toestanden en grootheden, en alles wat dit inhoudt over de manier waarop kwantummechanische systemen zich gedragen, zijn allemaal verweven in de structuur van deze ruimten, belichaamd in de relaties tussen de wiskundige objecten die hen weergeven. Dit betekent dat begrijpen hoe een systeem er volgens de kwantummechanica uitziet, onlosmakelijk verbonden is met vertrouwd zijn met de interne structuur van deze ruimten. Als je je weg weet in de Hilbert-ruimte, en vertrouwd raakt met de dynamische wetten die de paden beschrijven die vectoren door die ruimte afleggen, dan weet je alles wat er te weten valt, in de termen van de theorie, over de systemen die zij beschrijft.
Met “je weg weten” in de Hilbert-ruimte bedoel ik iets meer dan er een beschrijving of een kaart van te bezitten; iedereen die een leerboek over quantummechanica op zijn plank heeft staan, heeft dat. Ik bedoel er de weg in weten zoals je de weg weet in de stad waarin je woont. Dit is een praktisch soort kennis dat in gradaties komt en het best wordt verworven door te leren problemen van de vorm op te lossen: Hoe kom ik van A naar B? Kan ik daar komen zonder door C te gaan? En wat is de kortste route? Afgestudeerde natuurkundestudenten brengen lange jaren door om vertrouwd te raken met de hoeken en gaten van de Hilbert-ruimte, om bekende oriëntatiepunten te vinden, om de platgetreden paden te bewandelen, om te leren waar geheime doorgangen en doodlopende wegen liggen, en om een gevoel te ontwikkelen voor de algemene indeling van de ruimte. Zij leren door de Hilbert-ruimte te navigeren zoals een taxichauffeur door zijn stad leert navigeren.
Hoeveel van dit soort kennis is nodig om de filosofische problemen te benaderen die met de theorie samenhangen? In het begin niet veel: alleen de meest algemene feiten over de geometrie van het landschap (dat in ieder geval, in tegenstelling tot dat van de meeste steden, prachtig georganiseerd is), en de paden die (de vectoren die de toestanden van) systemen er doorheen afleggen. Dat is wat hier zal worden voorgesteld: eerst wat eenvoudige wiskunde, en dan, in een notendop, de theorie.
Wiskunde
2.1 Vectoren en vectorruimten
Een vector (A), geschreven ‘\ket{A}\)’, is een wiskundig object dat gekenmerkt wordt door een lengte, \(A||), en een richting. Een gestandaardiseerde vector is een vector met lengte 1; d.w.z. \(|A| = 1). Vectoren kunnen worden opgeteld, vermenigvuldigd met constanten (inclusief complexe getallen), en met elkaar vermenigvuldigd. Optellen van vectoren brengt elk paar vectoren over op een andere vector, meer bepaald de vector die je krijgt door de staart van de tweede vector zo te verschuiven dat hij samenvalt met de top van de eerste, zonder de lengte of de richting van beide te veranderen, en dan de staart van de eerste te verbinden met de top van de tweede. Deze optelregel staat bekend als de wet van het parallellogram. Bijvoorbeeld, optelling van de vectoren (\ket{A}) en \ket{B}) geeft de vector \ket{C} (= \ket{A} + \ket{B})\) zoals in figuur 1:
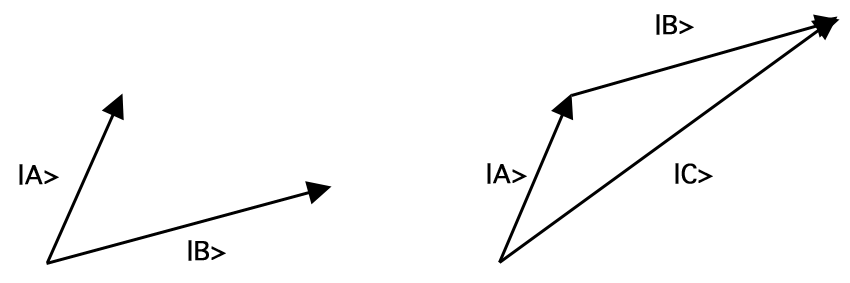
Figuur 1.Vectoroptelling
Vermenigvuldiging van een vector \(\ket{A})\) met \(n), waarbij \(n) een constante is, geeft een vector die dezelfde richting heeft als \(\ket{A})\, maar waarvan de lengte gelijk is aan \(n) maal de lengte van \(\ket{A}}).
In een reële vectorruimte is het (inwendig of scalair) product van een paar vectoren \(\ket{A}}) en \(\ket{B}}), geschreven ‘\(\braket{A}{B}})’ een scalair gelijk aan het product van hun lengten (of ‘normen’) maal de cosinus van de hoek, \(\theta}), tussen hen:
>Laat \(\ket{A_1}} en \(\ket{A_2}}) vectoren van lengte 1(“eenheidsvectoren”) zijn zo dat \(\ket{A_1}{A_2} = 0). (De hoek tussen deze twee eenheidsvectoren moet 90 graden zijn.) Dan kunnen we elke tweedimensionale vector \(\ket{B}}) als volgt voorstellen in termen van onze eenheidsvectoren:
Hier ziet u bijvoorbeeld hoe \ket{B} kan worden voorgesteld als de som van de twee eenheidsvectoren \ket{A_1}\ en \ket{A_2}\:
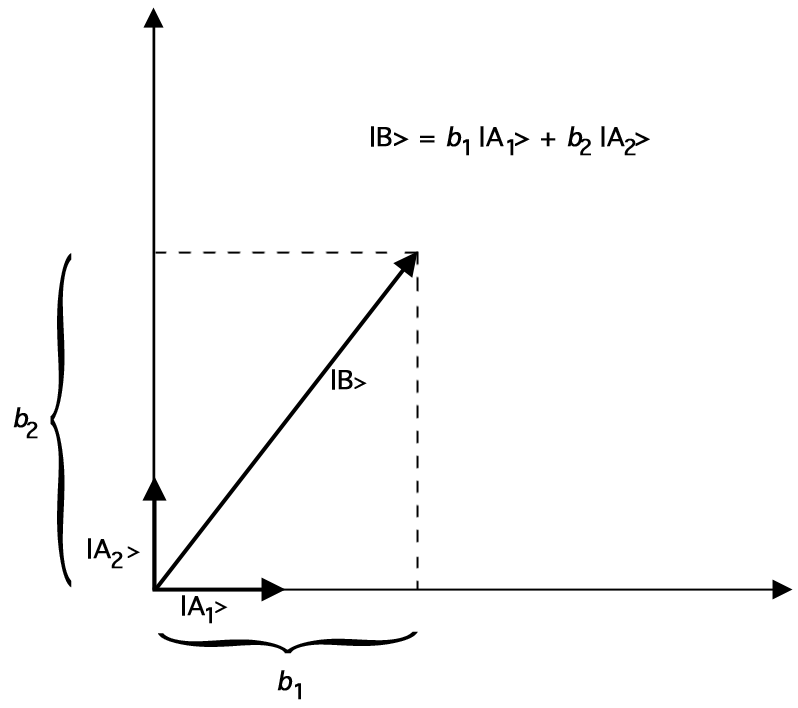
Figuur 2.Voorstelling van \(\ket{B}) door vectoroptelling van eenheidsvectoren
Nu moet de definitie van het inwendig product \(\ket{A}{B}) aangepast worden om toe te passen op complexe ruimten. Zij het complexconjugaat van c. (Als \(c) een complex getal is van de vorm \(a \pm bi), dan is de complexconjugaat van \(c) als volgt gedefinieerd:
^* = a-bi \^* = a+bi)
Dus, voor alle complexe getallen \(c), ^* = c), maar \(c^* = c) alleen in het geval dat \(c) reëel is). De definitie van het inwendig product van \ket{A}} en \ket{B}} voor complexe ruimten kan als volgt gegeven worden in termen van de conjugaten van complexe coëfficiënten. Waarbij (ket{A_1}} en (ket{A_2}} de eerder beschreven eenheidsvectoren zijn, \(ket{A} = a_1 ket{A_1} + a_2 ket{A_2}) en \(ket{B} = b_1 ket{A_1} + b_2 ket{A_2}), dan
Het meest algemene en abstracte begrip van een inwendig product, waarvan we nu twee speciale gevallen hebben gedefinieerd, is als volgt. \(\braket{A}{B}}) is een binnenproduct op een vectorruimte \(V) voor het geval
- (\braket{A}{A} = |A|^2), en (\braket{A}{A}=0) als en slechts als \(A=0})
- (\braket{B}{A} = \braket{A}{B}^*)
- (\braket{B}{A+C}= \braket{B}{A} + \braket{B}{C}).
Daaruit volgt dat
- de lengte van (\ket{A}) de vierkantswortel is van het binnenproduct van \ket{A}} met zichzelf, dus,\
- (\ket{A}} en \(\ket{B}}) staan onderling loodrecht op elkaar, of orthogonaal, als en slechts als \(\ket{A}{B}}).
Een vectorruimte is een verzameling vectoren die kan worden opgeteld en vermenigvuldigd met constanten; een inwendige productruimte is een vectorruimte waarop de vectormultiplicatie is gedefinieerd, en de dimensie van zo’n ruimte is het maximale aantal niet-nul, onderling loodrechte vectoren die zij bevat.
Elke verzameling van \(N\)- onderling loodrechte vectoren van lengte 1 in een vectorruimte van dimensie vormt een orthonormale basis voor die ruimte. Zij zo’n verzameling eenheidsvectoren. Dan kan elke vector in de ruimte uitgedrukt worden als een som van de vorm:
waarbij b_i = \braket{B}{A_i}\). De b_i’s zijn hier bekend als de expansiecoëfficiënten van B in de A-basis.
Merk op dat:
- voor alle vectoren A, B, en C in een gegeven ruimte, voor alle vectoren M en Q, uitgedrukt in termen van de A-basis,
en
Er is een andere manier om vectoren te schrijven, namelijk door de expansiecoëfficiënten (ten opzichte van een gegeven basis) in een kolom te schrijven, zoals:
waarbij q_i = qbraket{Q}{A_i} en de \(A_i}) de gekozen basisvectoren zijn.
Wanneer we te maken hebben met vectorruimten van oneindige dimensie, dan kunnen we niet de hele kolom uitdijingscoëfficiënten opschrijven die nodig is om een vector te berekenen, omdat die dan oneindig lang zou moeten zijn; in plaats daarvan schrijven we de functie op (de “golffunctie” genoemd voor q, gewoonlijk voorgesteld als \psi(i))\) die deze coëfficiënten als waarde heeft. We schrijven de functie als volgt op:
>Gegeven aan een willekeurige vector in, en aan een willekeurige basis voor, een vectorruimte, kunnen we de golffunctie van de vector in die basis afleiden; en gegeven aan een golffunctie voor een vector, in een bepaalde basis, kunnen we de vector construeren waarvan de golffunctie is. Aangezien blijkt dat de meeste belangrijke bewerkingen op vectoren overeenkomen met eenvoudige algebraïsche bewerkingen op hun golffuncties, is dit de gebruikelijke manier om staatvectoren voor te stellen.
Wanneer een paar fysische systemen op elkaar inwerken, vormen zij een samengesteld systeem, en zowel in de kwantummechanica als in de klassieke mechanica is er een regel om de toestandsruimte van een samengesteld systeem te construeren uit die van zijn componenten, een regel die ons vertelt hoe we uit de toestandsruimten H_A en H_B voor respectievelijk H_A en H_B de toestandsruimte – het tensorproduct van H_A en H_B genoemd, en geschreven H_A maal H_B – van het paar kunnen verkrijgen. Er zijn twee belangrijke dingen aan deze regel; ten eerste, zolang H_A en H_B Hilbertruimten zijn, zal H_A en H_B dat ook zijn, en ten tweede, er zijn enkele feiten over de manier waarop H_A zich verhoudt tot H_A en H_B, die verrassende gevolgen hebben voor de relaties tussen het complexe systeem en zijn onderdelen. In het bijzonder blijkt dat de toestand van een samengesteld systeem niet uniek bepaald is door die van zijn componenten. Wat dit betekent, of althans wat het lijkt te betekenen, is dat er volgens de kwantummechanica feiten zijn over samengestelde systemen (en niet alleen feiten over hun ruimtelijke configuratie) die niet superieur zijn aan feiten over hun componenten; het betekent dat er feiten zijn over systemen als gehelen die niet superieur zijn aan feiten over hun onderdelen en de manier waarop die onderdelen zijn gerangschikt ter plaatse. Het belang van dit kenmerk van de theorie kan niet worden overschat; het is, op de een of andere manier, betrokken bij de meeste van haar moeilijkste problemen.
In een beetje meer detail: Als \(v_{i}^A}) een orthonormale basis is voor \(H_A) en \(uu_{j}^B}) een orthonormale basis is voor \(H_B), dan wordt de verzameling van paren \((v_{i}^A, u_{j}^B)\) geacht een orthonormale basis te vormen voor de tensorproductruimte \(H_A \ maal H_B). De notatie v_i^A maal u_j^B wordt gebruikt voor het paar v_{i}^A,u_{j}^B), en het inwendig product op H_A maal H_B wordt gedefinieerd als:
- elke samengestelde toestand de toestanden van zijn componenten op unieke wijze definieert.
- als de toestanden van A en B zuiver zijn (d.w.z., representeerbaar door respectievelijk de v^A en u^B, dan is de toestand van A+B zuiver en representeerbaar door v^A maal u^B, en
- als de toestand van A+B zuiver is en kan worden uitgedrukt in de vorm v^A maal u^B, dan zijn de toestanden van A en B zuiver, maar
- als de toestanden van A en B niet zuiver zijn, d.w.z.e., als het gemengde toestanden zijn (deze worden hieronder gedefinieerd), bepalen zij niet op unieke wijze de toestand van (A+B); in het bijzonder kan het een zuivere toestand zijn die niet kan worden uitgedrukt in de vorm (v^A maal u^B).
2.2 Operatoren
Een operator (O) is een afbeelding van een vectorruimte naar zichzelf; hij brengt een willekeurige vector (\ket{B}}) in een ruimte over in een andere vector \(\ket{B’}}) ook in de ruimte; \(O \ket{B} = \ket{B’}}). Lineaire operatoren zijn operatoren die de volgende eigenschappen hebben:
- (O(\ket{A} + \ket{B}) = O \ket{A} + O ket{B}), en
- (O(c ket{A}) = c(O ket{A})\).
Net zoals elke vector in een ndimensionale ruimte kan worden voorgesteld door een kolom van ndimensionale getallen, ten opzichte van een keuze van basis voor de ruimte, kan elke lineaire operator op de ruimte worden voorgesteld in een kolomnotatie door ndimensionale getallen:
waarin O_{ij} = O_{A_i}{O A_j}) en de A_N de basisvectoren van de ruimte zijn. Het effect van de lineaire operator O op de vector B is dan als volgt: Nog twee definities voordat we kunnen zeggen wat Hilbertruimten zijn, en dan kunnen we overgaan tot de kwantummechanica. \(ket{B}) is een eigenvector van O met de eigenwaarde a als en slechts als O ket{B} = a ket{B}).Verschillende operatoren kunnen verschillende eigenvectoren hebben, maar de eigenvector/operator-relatie hangt alleen af van de operator en de vectoren in kwestie, en niet van de specifieke basis waarin zij worden uitgedrukt; de eigenvector/operator-relatie is, d.w.z., invariant onder verandering van basis. Een Hermitische operator is een operator die de eigenschap heeft dat er een orthonormale basis bestaat uit zijn eigenvectoren en dat die eigenwaarden alle reëel zijn.
Een Hilbert-ruimte tenslotte is een vectorruimte waarop een inproduct gedefinieerd is, en die volledig is, d.w.z. zo dat elke Cauchy-reeks van vectoren in de ruimte convergeert naar eenvector in de ruimte. Alle eindig-dimensionale binnenproductruimten zijn volledig, en ik zal mij hiertoe beperken. Het oneindige gevalinvolgt enkele complicaties die in dit stadium niet vruchtbaar zijn.
Kwantummechanica
Vier basisprincipes van de kwantummechanica zijn:
(3.1)
Fysische toestanden.Elk fysisch systeem is geassocieerd met een Hilbert-ruimte, elke eenheidsvector in de ruimte correspondeert met een mogelijke zuivere toestand van het systeem, en elke mogelijke zuivere toestand, met een of andere vector in de ruimte.
(3.2)
Fysische Grootheden.Hermitische operatoren in de Hilbert-ruimte geassocieerd met een systeem vertegenwoordigen fysische grootheden, en hun eigenwaarden vertegenwoordigen de mogelijke resultaten van metingen aan die grootheden.
Er is een operator, de Hamiltoniaan, die een speciale rol speelt in de kwantumtheorie omdat de dynamica van een systeem gemakkelijk kan worden geformuleerd door de evolutie ervan te volgen. De Hamiltoniaan – geschreven als H(H), of H(Hat{H}) – staat voor de totale energie van het systeem. De eigenwaarden zijn de mogelijke resultaten die bij metingen van de totale energie kunnen worden verkregen. Zij wordt verkregen door de kinetische en potentiële energieën van de componenten van het systeem bij elkaar op te tellen.
(3.3)
Samenstelling.De Hilbertruimte die hoort bij een complex systeem is het tensorproduct van die van de eenvoudige systemen (in de standaard, niet-relativistische, theorie: de afzonderlijke deeltjes) waaruit het is samengesteld.
(3.4) Dynamica. a.
Contexten van type 1: Gegeven de toestand van een systeem op elk tijdstip en de krachten en beperkingen waaraan het onderworpen is, bestaat er een vergelijking, de “Schrödinger-vergelijking”, die de toestand op elk ander tijdstip geeft \(Uket{v_t} \rechtsdraaiend \ket{v_{t’}}). De voor ons belangrijke eigenschappen van \(U) zijn dat ze deterministisch is, dat wil zeggen dat ze de toestand van een systeem op een bepaald tijdstip in een unieke toestand op een ander tijdstip brengt, dat ze unitair is, dat wil zeggen dat ze een automorfisme is van de Hilbert-ruimte waarop ze werkt (d.w.z, een afbeelding van die ruimte op zichzelf die de lineaire ruimtestructuur en het inwendig product behoudt), en ze is lineair, wat wil zeggen dat als ze een toestand(\ket{A}) overneemt in de toestand(\ket{A’}), en hij neemt de toestand \ket{B}} over de toestand \ket{B’}}, dan neemt hij elke toestand van de vorm \(\alpha \ket{A} + \beta \ket{B’}}) over de toestand \(\alpha \ket{A’} + \beta \ket{B’}}).
b.
Contexten van type 2 (“Meetcontexten”): Het uitvoeren van een “meting” aan een waarneembaar \ket{A}} op een systeem in een toestand \ket{A}} heeft tot gevolg dat het systeem ineenstort tot een \ket{A}}-eigen toestand die overeenkomt met de waargenomen eigenwaarde. Dit staat bekend als het instortingsPostulaat. In welke specifieke eigenwaarde-toestand het instort is een kwestie van waarschijnlijkheid, en de waarschijnlijkheden worden gegeven door een regel die bekend staat als de regel van Born:
Er zijn twee belangrijke punten op te merken over deze twee soorten contexten:
- Het onderscheid tussen contexten van type 1 en 2 moet nog worden gemaakt in kwantummechanische termen; niemand is erin geslaagd om op een volledig bevredigende manier, in de termen die door de theorie worden aangereikt, te zeggen welke contexten meetcontexten zijn, en
- Zelfs als het onderscheid is gemaakt, is het een open interpretatieve vraag of er contexten van type 2 bestaan; d.w.z.e., het is een open interpretatieve vraag of er contexten zijn waarin systemen worden beheerst door een andere dynamische regel dan de vergelijking van Schrödinger.
Structuren op de Hilbert-ruimte
Ik merkte hierboven op dat op dezelfde manier als alle informatie die we hebben over de relaties tussen plaatsen in een stad is belichaamd in de ruimtelijke relaties tussen de punten op een kaart die ze voorstellen, alle informatie die we hebben over de interne relaties tussen (en tussen) toestanden en grootheden in de kwantummechanica is belichaamd in de wiskundige relaties tussen de vectoren en operatoren die ze voorstellen. Vanuit wiskundig oogpunt onderscheidt de kwantummechanica zich van haar klassieke voorgangers doordat toestanden en grootheden een rijkere structuur hebben; zij vormen families met een interessanter netwerk van relaties tussen hun leden.
Alle fysische consequenties van het gedrag van kwantummechanische systemen zijn gevolgen van wiskundige eigenschappen van die relaties, en de belangrijkste daarvan zijn gemakkelijk samen te vatten:
(P1)
Elke manier om vectoren in een Hilbert-ruimte op te tellen of te vermenigvuldigen met scalaren levert een vector op die ook in de ruimte is. In het geval dat de vector genormaliseerd is, zal hij op grond van (3.1) een mogelijke toestand van het systeem voorstellen, en in het geval dat hij de som is van een paar eigenvectoren van een waarneembare variabele met verschillende eigenwaarden, zal hij zelf geen eigenvector van het systeem zijn, maar zal hij op grond van (3.4b) geassocieerd zijn met een reeks waarschijnlijkheden voor het tonen van het ene of het andere resultaat in waarnemingen.
(P2)
Voor elke Hermitische operator op een Hilbertruimte zijn er andere, op dezelfde ruimte, waarmee hij geen volledige verzameling eigenvectoren gemeen heeft; het is inderdaad gemakkelijk aan te tonen dat er andere zulke operatoren zijn waarmee hij geen eigenvectoren gemeen heeft.
Als we een paar aanvullende interpretatieve aannamen doen, kunnen we meer zeggen. Neem bijvoorbeeld aan dat
(4.1)
Elke Hermitische operator op de Hilbert-ruimte die met een systeem geassocieerd is, vertegenwoordigt een afzonderlijke observabele, en (dus)elke genormaliseerde vector, een afzonderlijke toestand, en
(4.2)
Een systeem heeft een waarde voor de observabele (A) als, en alleen als, de vector die zijn toestand vertegenwoordigt, een eigenstaat is van de (A) operator. De waarde die het in zo’n geval heeft, is gewoon de eigenwaarde die bij die eigenwaarde hoort.
Uit (P2) volgt uit (3.1) dat geen enkele kwantummechanische toestand een eigenwaarde is van alle waarneembaarheden (en dat er inderdaad waarneembaarheden zijn die geen eigenwaarden gemeen hebben), en dus volgt uit (3.2) dat geen enkele kwantummechanische toestand een eigenwaarde is van alle waarneembaarheden (en dat er inderdaad waarneembaarheden zijn die geen eigenwaarden gemeen hebben).2), dat geen enkel kwantummechanisch systeem ooit gelijktijdige waarden heeft voor alle grootheden die erbij horen (en dat er inderdaad paren van grootheden zijn waaraan geen enkele toestand gelijktijdige waarden toekent).
Er zijn Hermitische operatoren op het tensorproduct (H_1 maal H_2) van een paar Hilbertruimten (H_1) en (H_2) … In het geval dat H_1 en H_2 de toestandsruimten zijn van de stelsels S1 en S2, dan is H_1 en H_2 de toestandsruimte van het complexe stelsel S1+S2. Hieruit volgt uit (4.1) dat er waarneembaarheden zijn die betrekking hebben op (S1+S2) waarvan de waarden niet bepaald worden door de waarden van waarneembaarheden die betrekking hebben op de twee afzonderlijk.
Dit zijn allemaal eenvoudige gevolgen van het nemen van vectoren en operatoren in de Hilbert-ruimte om respectievelijk toestanden en waarneembaarheden voor te stellen, en het toepassen van de Regel van Born (en later (4.1) en (4.2)), om empirische betekenis te geven aan toestands-toewijzingen. Zoveel is perfect begrepen; de echte moeilijkheid bij het begrijpen van de kwantummechanica ligt in het vat krijgen op hun implicaties – fysisch, metafysisch en epistemologisch.
Iedereen die probeert te begrijpen wat de kwantummechanica zegt over de wereld, moet worstelen met één overblijvend feit. Dit probleem heeft niets te maken met Hilbert-ruimten, maar met de dynamica – de regels die de trajecten beschrijven die systemen door de ruimte volgen. Vanuit fysisch oogpunt is het veel zorgwekkender dan alles wat tot nu toe besproken is. Het levert niet alleen moeilijkheden op voor iemand die een interpretatie van de theorie probeert te geven, maar lijkt ook te wijzen op een logische inconsistentie in de grondslagen van de theorie.
Voorstel dat we een systeem hebben en een apparaat dat een waarneembaar gegeven meet op een systeem met waarden. Dan is er een toestand van ²(S^*) (de “grondtoestand”), en een waarneembare ²(B) met waarden ²(b_1, b_2,b_3, …\die horen bij S^* (de ‘wijzerwaarneembaar’, zo genoemd omdat deze de rol speelt van de wijzer op een wijzerplaat aan de voorkant van een schematisch meetinstrument bij het registreren van het resultaat van het experiment), die zodanig zijn dat, als (S^*) wordt gestart in zijn grondtoestand en op een geschikte manier interageert met (S), en als de waarde van (A) onmiddellijk voor de interactie gelijk is aan (a_1), dan is de waarde van (B) onmiddellijk daarna gelijk aan (b_1). Als echter de waarde van \(A) onmiddellijk voor de interactie \(a_2) is, dan is de waarde van \(B) daarna \(b_2); als de waarde van \(A) onmiddellijk voor de interactie \(a_3) is, dan is de waarde van \(B) onmiddellijk daarna \(b_3), enzovoort. Dat is precies wat het betekent om te zeggen dat de waarde van S^* gelijk is aan de waarde van A. Dus, als we de gezamelijke, gedeeltelijke toestand van S en S (alleen het deel ervan dat de waarde van de waarneembare specificeert, waarvan de waarden overeenkomen met gezamenlijke toewijzingen van waarden aan de gemeten waarneembare op S en de aanwijsbare waarneembare op S) voorstellen door de vector en laat “S^*” staan voor de dynamische beschrijving van de wisselwerking tussen de twee, om te zeggen dat “S^*” een meetinstrument is voor “A” is te zeggen dat de dynamische wetten met zich meebrengen dat,
enzovoort.
Uit de regels voor het verkrijgen van de toestandsruimte van het samengestelde systeem volgt dat de gecombineerde toestand van het paar
is, en het volgt uit het feit dat S^* een meetinstrument is voor S^*,en de lineariteit van hun gecombineerde toestand na interactie, is
Dit, echter, is inconsistent met de dynamische regel voor contexten van type 2, want de dynamische regel voor contexten van type 2 (en als er al zulke contexten zijn, dan is dit er een) houdt in dat de toestand van het paar na interactie ofwel
ofwel
Inderdaad, het houdt in dat er een precieze kans van \(\frac{1}{2}\) is dat het in de eerste toestand terechtkomt, en een kans van \(\frac{1}{2}\) dat het in de tweede toestand terechtkomt.
We kunnen proberen de logische consistentie te herstellen door de dynamische regel voor contexten van type 2 op te geven (of, wat op hetzelfde neerkomt, door te ontkennen dat er zulke contexten zijn), maar dan zitten we met het probleem van de consistentie met de ervaring. Want het was niet louter een blunder dat die regel in de theorie werd opgenomen; we weten hoe een systeem eruit ziet als het zich in een eigenstaat van een bepaalde waarneembare bevindt, en we weten door te kijken dat het meetapparaat zich na de meting in een eigenstaat van de aanwijsbare waarneembare bevindt. En dus weten we van meet af aan dat als een theorie ons iets anders vertelt over de toestanden van meetapparaten na de meting, wat dat andere dan ook moge zijn, het fout is.
Dat is, in een notendop, het meetprobleem in de kwantummechanica; elke interpretatie van de theorie, elk gedetailleerd verhaal over hoe de wereld er volgens de kwantummechanica uitziet, en in het bijzonder die stukjes van de wereld waarin metingen plaatsvinden, moet ermee worstelen.
Loose Ends
Gemengde toestanden zijn gewogen sommen van zuivere toestanden, en zij kunnen worden gebruikt om de toestanden van ensembles voor te stellen waarvan de componenten zich in verschillende zuivere toestanden bevinden, of toestanden van individuele systemen waarover wij slechts gedeeltelijke kennis hebben. In het eerste geval weerspiegelt het gewicht dat aan een gegeven zuivere toestand wordt toegekend de grootte van de component van het ensemble die in die toestand is (en dus de objectieve waarschijnlijkheid dat een willekeurig lid van het ensemble in die toestand is); in het tweede geval weerspiegelen zij de epistemische waarschijnlijkheid dat het systeem in kwestie waaraan de toestand wordt toegekend in die toestand is.
Als we het onderscheid tussen zuivere en gemengde toestanden niet willen verliezen, hebben we een manier nodig om de gewogen som van een stel zuivere toestanden (equivalent, van de waarschijnlijkheidsfuncties die ermee geassocieerd zijn) weer te geven die anders is dan het optellen van de (voldoende gewogen) vectoren die hen vertegenwoordigen, en dat betekent dat we ofwel een alternatieve manier nodig hebben om gemengde toestanden weer te geven, ofwel een uniforme manier om zowel zuivere als gemengde toestanden weer te geven die het onderscheid tussen hen bewaart.Er is een soort operator in Hilbertruimten, dichtheidsoperator genaamd, die goed dienst doet in de laatste hoedanigheid, en het blijkt niet moeilijk te zijn om alles wat gezegd is over toestandsvectoren te herformuleren in termen van dichtheidsoperatoren. Dus, hoewel het gebruikelijk is te spreken alsof zuivere toestanden worden voorgesteld door vectoren, is de officiële regel dat toestanden – zowel zuivere als gemengde – in de kwantummechanica worden voorgesteld door dichtheidsoperatoren.
Hoewel gemengde toestanden, zoals ik zei, kunnen worden gebruikt om onze onwetendheid van de toestanden van systemen die eigenlijk in een of andere zuivere toestand zijn weer te geven, en hoewel dit velen een adequate manier leek om mengsels in een klassieke context te interpreteren, zijn er serieuze obstakels om dit in het algemeen toe te passen op kwantummechanische mengsels. Deze worden overgelaten voor gedetailleerde bespreking in de andere ingangen over quantummechanica in de Encyclopedie.
Alles wat gezegd is over observabelen, strikt genomen, is alleen van toepassing op het geval waarin de waarden van het observabel een afzonderlijke set vormen; de wiskundige finesses die nodig zijn om het te veralgemenen naar het geval van continue observabelen zijn gecompliceerd, en geven problemen van een meer technische aard. Ook deze kunnen het beste in detail worden besproken.
Dit zou alle eerste voorbereiding moeten zijn die men nodig heeft om de filosofische discussie van de kwantummechanica te benaderen, maar het is slechts een eerste stap. Hoe meer men leert over de relaties tussen vectoren en operatoren in de Hilbert-ruimte, hoe de ruimten van eenvoudige systemen zich verhouden tot die van complexe systemen, en over de vergelijking die beschrijft hoe toestandsvectoren door de ruimte bewegen, hoe beter men zowel de aard als de moeilijkheidsgraad van de problemen die met de theorie samenhangen, zal kunnen inschatten. Het grappige aan de kwantummechanica, datgene wat het voor een filosoof eindeloos boeiend maakt, is dat hoe meer men leert, hoe moeilijker de problemen worden.