Mecânica Quântica
Terminologia
Sistemas físicos são divididos em tipos de acordo com suas propriedades imutáveis (ou ‘state-independent’), e o estado de um sistema de cada vez consiste em uma especificação completa daquelas de suas propriedades que mudam com o tempo (suas propriedades ‘state-dependent’). Para dar uma descrição completa de um sistema, então, precisamos dizer que tipo de sistema ele é e qual é o seu estado em cada momento da sua história.
Uma quantidade física é uma família de propriedades físicas mutuamente exclusivas e conjuntamente exaustivas (para aqueles que conhecem esta forma de falar, é uma família de propriedades com a estrutura das células em uma partição). Saber que tipos de valores uma quantidade pode nos dizer muito sobre as relações entre as propriedades de que ela é composta. Os valores de uma quantidade bivalente, forinstância, formam um conjunto com dois membros; os valores de uma quantidade de valor real formam um conjunto com a estrutura dos números reais. Este é um caso tão especial de algo que veremos repetidamente, a saberque saber que tipo de objetos matemáticos representam os elementos de algum conjunto (aqui, os valores de uma quantidade física; mais tarde, os estados que um sistema pode assumir, ou as quantidades pertencentes a ele) diz-nos muito (de fato, possivelmente, tudo o que há para saber) sobre as relações entre eles.
Em contextos mecânicos quânticos, o termo “observável” é usado indistintamente com “quantidade física”, e deve ser tratado como um termo técnico com o mesmo significado. Não é por acaso que o desenvolvedor precoce da teoria escolheu o termo, mas a escolha foi feita por razões que não são, hoje em dia, geralmente aceitas. O estado-espaço de um sistema é o espaço formado pelo conjunto dos seus estados possíveis, ou seja, as formas fisicamente possíveis de se obter os valores das quantidades que o caracterizam internamente. Teorias clássicas, um conjunto de quantidades que forma uma base de superveniência para o resto é tipicamente designado como ‘básico’ ou ‘fundamental’, e, como qualquer forma matematicamente possível de combinar os seus valores é uma possibilidade física, o espaço-espaço de estados pode ser obtido simplesmente tomando estes como coordenadas. Assim, por exemplo, o espaço-estado de um sistema mecânico clássico composto por partículas, obtido especificando os valores de quantidades de valor real – três componentes de posição e três de momento para cada partícula do sistema – é um espaço de coordenadas dimensionais. Cada possível estado do sistema sucha corresponde a um ponto no espaço, e cada ponto no espaço corresponde a um possível estado de tal sistema. A situação é um pouco diferente na mecânica quântica, onde existem formas matematicamente descritíveis de combinar os valores das grandezas que não representam estados fisicamente possíveis. Como veremos, os espaços de estado da mecânica quântica são tipos especiais de espaços vectoriais, conhecidos como espaços Hilbert, e têm mais estrutura interna do que os seus equivalentes clássicos.
Uma estrutura é um conjunto de elementos sobre os quais certas operações e relações são definidas, uma estrutura matemática é apenas uma estrutura em que os elementos são objectos matemáticos (números, conjuntos, vectores) e as operações matemáticas, e um modelo é uma estrutura matemática usada para representar alguma estrutura fisicamente significativa no mundo.
O coração e a alma da mecânica quântica estão contidos nos espaços de Hilbertspaces que representam os espaços de estados dos sistemas mecânicos quânticos. As relações internas entre estados e quantidades, e tudo o que esteentails sobre a forma como os sistemas mecânicos quânticos se comportam, estão todos tecidos na estrutura desses espaços, incorporados nas relações entre os objetos matemáticos que os representam. Isto significa que, ao compreender como é um sistema de acordo com a mecânica quântica, é possível enxaguar a familiaridade com a estrutura interna desses espaços. Conhecer o espaço Hilbert e familiarizar-se com as leis dinâmicas que descrevem os caminhos que os vectores percorrem, e saber tudo o que há para saber, nos termos fornecidos pela teoria, sobre os sistemas que ela descreve.
Por ‘conhecer o espaço Hilbert’, quero dizer algo mais do que possuir uma descrição ou um mapa dele; qualquer pessoa que tenha um livro de mecânica quântica na sua prateleira tem isso. Quero dizer, conhecer o seu caminho na forma como você conhece a cidade em que vive. Este é um tipo prático de conhecimento que vem de indegrees e é melhor adquirido aprendendo a resolver problemas da forma: Como é que eu passo de A para B? Posso chegar lá sem passar porC? E qual é o caminho mais curto? Estudantes de graduação em Física passam anos se familiarizando com os recantos de Hilbertspace, localizando pontos de referência familiares, trilhando seus caminhos batidos, aprendendo onde há passagens secretas e becos sem saída, e desenvolvendo uma sensação de que a terra é um todo. Eles aprendem como navegar no espaço de Hilbert no caminho que um taxista aprende a navegar na sua cidade.
Quanto deste tipo de conhecimento é necessário para abordar os problemas filosóficos associados à teoria? No início, não muito: apenas os fatos mais gerais sobre a geometria da paisagem (que é, de qualquer forma, diferente da da maioria das cidades, belamente organizada), e os caminhos que (os vetores que representam os estados dos) sistemas percorrem através deles. Isso é o que será introduzido aqui: primeiro um pouco de matemática fácil, e depois, em poucas palavras, a teoria.
Matemática
2.1 Vectores e espaços vectoriais
Um vector {\an8}, escrito ‘\an8}, é um objecto matemático caracterizado por um comprimento, {\an8}, e uma direcção. Vetor anormalizado é um vetor de comprimento 1; isto é, |A| = 1 Os vetores podem ser adicionados juntos, multiplicados por constantes (incluindo números complexos), e multiplicados juntos. A adição de vetores mapeia qualquer par de vetores em outro vetor, especificamente, aquele que você obtém movendo o segundo vetor de forma que sua cauda coincida com a ponta do primeiro, sem alterar o comprimento ou a direção de nenhum dos dois, e então unindo a cauda do primeiro à ponta do segundo. Esta regra de adição é conhecida como a lei do paralelogramo. Assim, por exemplo, a adição de vetores de produção (ket (A) e (B)) produz vetores de produção (ket (C)). (= {A} + {B})} asin Figura 1:
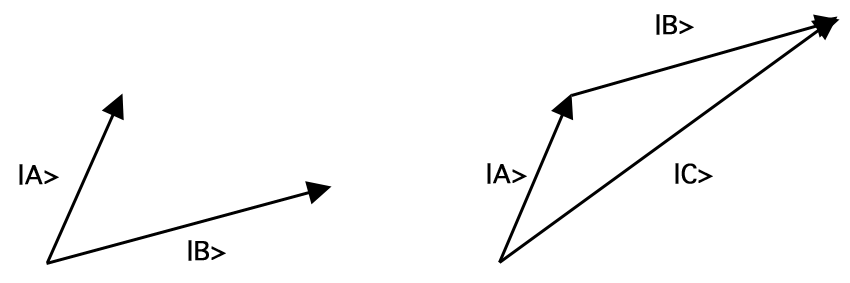
Figura 1.Adição de vetores
Multiplicação de um vetor por um comprimento constante, dá um vetor que é a mesma direção que o comprimento do desenho, mas cujo comprimento é vezes o comprimento do desenho.
Num espaço vectorial real, o produto (interior ou ponto) de um par de vectores e o “traquete”, escrito “traquete”, é um escalar igual ao produto dos seus comprimentos (ou “normas”) vezes o cosseno do ângulo, entre eles:
Let {A_1}(A_1}) e {A_2}) sejam vectores de comprimento 1(“vectores de unidade”) tais que {A_1}{A_2} = 0}). (O ângulo entre esses dois vetores unitários deve ser de 90 graus). Então wecan representa qualquer vetor bidimensional em termos dos nossos vetores unitários como segue:
Por exemplo, aqui está um gráfico que mostra como pode ser representado como a soma dos dois vectores de unidade:
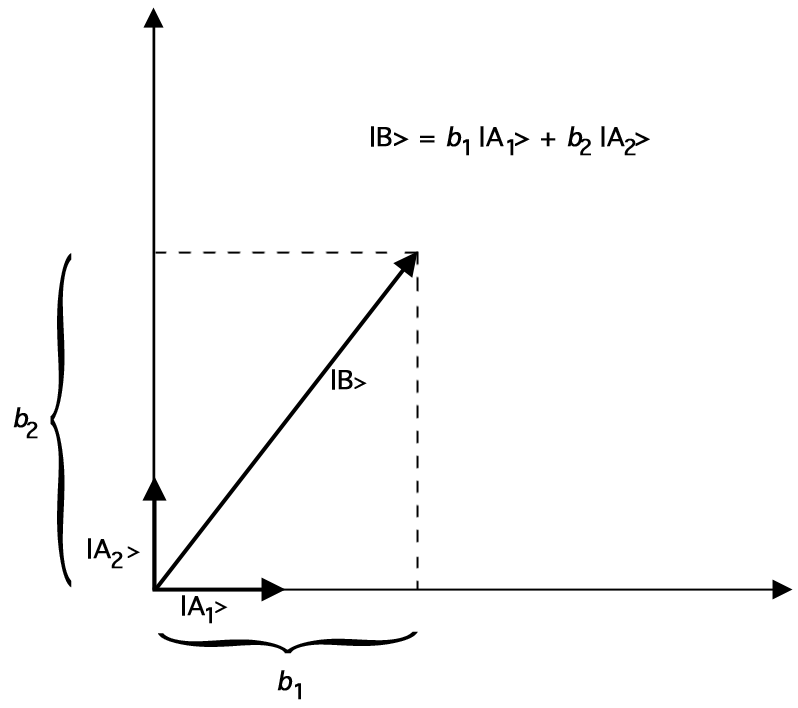
Figure 2.Representando {B}{B}) por Vector Adição de Vectores de Unidade
Agora a definição do produto interior {A}{B}} tem de ser bemodificada para se aplicar a espaços complexos. Que seja o conjugado completo da c^*). Quando o número complexo da forma é um número complexo, então o conjugado complexo é definido da seguinte forma:
> = a-bi = a+bi
Então, para todos os números complexos, mas no caso de ser real… A definição do produto interno do esboço e do esboço B para o espaço-espaço complexo deve ser dada em termos de conjugação de coeficientes complexos. Onde os vetores unitários descritos anteriormente são: a_1 + a_2 e b_1 + b_2, então
\
A noção mais geral e abstracta de um produto interior, do qual definimos agora dois casos especiais, é a seguinte. \(A) é um produto de primeira num espaço vectorial (V) apenas no caso de
- (A) = |A|^2^), e {A}{A}{A=0}) se e só se
Disso decorre que
- o comprimento do {\an8}(A) é a raiz quadrada do produto interior do {\an8}(A) consigo mesmo, ou seja\
- (A) e B) são mutuamente perpendiculares, ortogonais, se, e só se, Braket (A) e B).
- para todos os vectores, B e C num determinado espaço,
- para quaisquer vectores e Q, expressos em termos da base A,
e
\
- qualquer estado composto define de forma única os estados dos seus componentes.
- se os estados de \(A) e \(B) são puros (i.e, são puros (i.e., os byvectores representáveis (v^A) e (u^B), respectivamente), então o estado de ((A+B)}) é puro e representado por ( v^A ^o vezes u^B)}, e
- se o estado de {(A+B)} é puro e expressável na forma de { v^A ^A ^B}, então os estados de ^(A) e B} são puros, mas
- se os estados de ^A e B} não são puros, i.e., se são estados mistos (estes são definidos abaixo), não definem de forma única o estado de ((A+B)); em particular, pode ser um estado puro não expressivo na forma…(v^A).
- \i(O(\i(A) + \i(B)) = O \i(A) + O {B}), e
- (O(c {A}) = c(O {A})}.
179
e 5992
- 455
Um espaço vectorial é um conjunto de vectores fechados com subadição, e multiplicação por constantes, um espaço de produtos interno é um espaço vectorial sobre o qual a operação de vectormultiplicação foi definida, e a dimensão desse espaço é o número máximo de vectores não-zero, mutuamente ortogonais, que contém.
Uma colecção de vectores mutuamente ortogonais de comprimento 1 num espaço vectorial dimensional constitui uma base orto-normal para esse espaço. Deixemos que os pontos, os pontos, os esboços sejam uma colecção de vectores unitários. Então cada vetor no espaço pode ser expresso como uma soma da forma:
onde {b_i = {B}{A_i}). Os coeficientes de expansão da base A são conhecidos como os coeficientes de expansão da base B.
Notem isso:
Há outra forma de escrever vectores, nomeadamente escrevendo os coeficientes de expansão (relativos a uma dada base) numa coluna, como por exemplo:
onde \\(q_i = {Q}{A_i}}) e os \\pos(A_i}) são os vectores de base escolhidos.
Quando estamos a lidar com espaços vectoriais de dimensão infinita, uma vez que não podemos escrever toda a coluna de coeficientes de expansão necessários, topick out um vector uma vez que teria de ser infinitamente longo, então em vez disso escrevemos a função (chamada ‘wave function’ for\\(Q\), normalmente representada por \psi(i))} que tem esses coeficientes como valores. Nós anotamos, isto é, a função:
\\
Dando qualquer vetor em, e qualquer base para, um espaço vetorial, podemos obter a função onda-função do vetor nessa base; e dada uma função onda-função para um vetor, em uma base particular, podemos construir o vetor cuja função onda-função é. Uma vez que a maioria das operações importantes sobre vectores correspondem a simples operações algébricas sobre as suas funções de onda, esta é a forma usual de representar os vectores-estado.
Quando um par de sistemas físicos interagem, eles formam um sistema composto, e, na mecânica quântica como na mecânica clássica, existe uma regra para construir o estado-espaço de um sistema composto a partir daqueles de seus componentes, uma regra que nos diz como obter, dos espaços-estaestaestaestais, (H_A) e (H_B), respectivamente, o espaço-estado – chamado ‘produto tensor’ de H_A) e H_B), e escrito (H_A) – do par. Há duas coisas importantes sobre a regra; primeiro, desde que os espaços Hilbert (H_A) e H_B) sejam espaços Hilbert (H_A) e H_B (H_A) também serão, e segundo, há alguns fatos sobre o modo como H_A se relaciona com H_A) e H_B (H_B), que têm conseqüências surpreendentes para a relação entre o sistema complexo e suas partes. Em particular, verifica-se que o estado de um sistema composto não é definido de forma única pelos seus componentes. O que isto significa, ou pelo menos o que parece tomaran, é que existem, de acordo com a mecânica quântica, fatos sobre sistemas compostos (e não apenas fatos sobre sua configuração espacial) que não se sobrepõem a fatos sobre seus componentes; significa que existem fatos sobre sistemas como atacado que não se sobrepõem a fatos sobre suas partes e a maneira como essas partes estão dispostas inspiram. O significado desta característica da teoria não pode ser superado; ela está, de uma forma ou de outra, implicada na maioria dos problemas mais difíceis.
Em um pouco mais de detalhe: se a teoria é uma base orthonormal para o espaço do produto tensor (H_B), então o conjunto de pares é tomado para formar uma base anorthonormal para o espaço do produto tensor (H_B). Thenotation {\i}(v_i^A {\i^A {j^B}) é usado para o par ((v_{i}^A,u_{j^B)}), e produto interior em H_A {j^B)} é definido como:
É um resultado desta construção que embora cada vector no espaço seja uma soma linear de vectores exprimível na forma {\i}(v^A ^A ^o vezes u^B\), nem todos os vectores no espaço são por si só exprimíveis nessa forma, e acontece que
2. Os operadores lineares são operadores que têm as seguintes propriedades:
Just as any vector in an {N^2}dimensional space can be represented by acolumn of {N^2} numbers, relative to a choice of basis for the space, anylinear operator on the space can be represented in a column notation by{N^2} numbers:
onde { O_{ij} = {A_i}{O {mid A_j}} e o {A_N} são os vectores base do espaço. O efeito do operador linear (O) no vector (B) é, então, dado por
Mais duas definições antes de podermos dizer o que são os espaços de Hilbert, e então podemos recorrer à mecânica quântica. \é um vector próprio com valor próprio se, e só se, “O” esboço = um esboço.Operadores diferentes podem ter vetores próprios diferentes, mas a relação operador/vetor próprio depende apenas do operador e vetor em questão, e não da base particular na qual eles são expressos; a relação operador/vetor próprio é, ou seja, invariante sob mudança de base. Um operador hermitiano é um operador que tem a propriedade de que existe uma base orthonormal que consiste nos seus auto-vectores e esses auto-valores são todos reais.
Um espaço Hilbert, finalmente, é um espaço vetorial sobre o qual um produto interno é definido, e que é completo, ou seja, que é tal que qualquer seqüência Cauchy de vetores no espaço converge para avetor no espaço. Todos os espaços de produto interno finitos-dimensionais são completos, e eu me restrinjo a estes. O caso infinito envolve algumas complicações que não são frutíferas nesta fase.
Mecânica Quântica
Quatro princípios básicos da mecânica quântica são:
(3.1)
Estados Físicos. Cada sistema físico está associado a um Espaço Hilbert, cada unitvector no espaço corresponde a um possível estado puro do sistema, e cada possível estado puro, a algum vector no espaço.
(3.2)
Quantidades Físicas. Os operadores hermitianos no espaço Hilbert associados a um sistema representam quantidades físicas, e os seus valores próprios representam os resultados possíveis das medições dessas quantidades.
Existe um operador, chamado Hamiltoniano, que desempenha um papel especial na teoria quântica, pois a dinâmica de um sistema pode ser formulada de forma mais ou menos rápida, acompanhando a sua evolução. O Hamiltoniano – escrito em Hamiltoniano (H), ou Hhat (H) – representa a totalidade da energia do sistema. Seus valores próprios são os possíveis resultados que podem ser obtidos em medições de energia total. É dado bysumming sobre as energias cinéticas e potenciais dos componentes do sistema.
(3,3)
Composição. O espaço Hilbert associado a um sistema complexo é o produto tensor daqueles associados aos sistemas simples (na teoria padrão, não-relativista: as partículas individuais) dos quais ele se compõe.
(3.4) Dinâmica. a.
Contextos de tipo 1: Dado o estado de um sistema em As propriedades importantes de U para os nossos fins são que é determinista, o que é dizer que leva o estado de um sistema de uma vez a um estado único em qualquer outro, é unitário, o que significa que é um automorfismo do espaço Hilbert sobre o qual actua (isto é.., que preserva a estrutura espacial linear e o produto interno), e é linear, o que quer dizer que se ele leva um estado para o estado.., e leva o estado para o estado (B), depois leva qualquer estado da forma (A) para o estado (A) para o estado (B).
b.
Contexos do tipo 2 (“Contextos de Medição”):Realizar uma “medição” de um asistema observável em um estado (B) tem o efeito de colapsar o sistema em um estado (B) -eigenstate correspondente ao valor próprio observado. Isto é conhecido como o CollapsePostulate. Em qual particular o {B)-eigenstate itcollapses é uma questão de probabilidade, e as probabilidades são dadas por uma regra conhecida como Born’s Rule:
Existem dois pontos importantes a notar sobre estes dois tipos de contextos:
- A distinção entre contextos de tipo 1 e 2 permanece por fazer em termos mecânicos quânticos; ninguém conseguiu dizer de forma totalmente satisfatória, nos termos fornecidos pela teoria, que contextos são contextos de medição, e
- Even, se a distinção for feita, é uma questão de interpretação aberta se existem contextos de tipo 2; i.e., é uma questão interpretativa aberta se existem contextos em que os sistemas são governados por uma regra dinâmica diferente da equação de Schrödinger.
Estruturas no Espaço Hilbert
Comentei acima que da mesma forma que toda a informação que temos sobre as relações entre os locais de uma cidade é incorporada nas relações espaciais entre os pontos de um mapa que os representam, toda a informação que temos sobre as relações internas entre (e entre) estados e quantidades na mecânica quântica é incorporada nas relações matemáticas entre os vetores e operadores que os representam. Do ponto de vista matemático, o que realmente distingue a mecânica quântica de suas predecessoras clássicas é que os estados e as quantidades têm uma estrutura mais rica; eles formam famílias com uma rede mais interessante de relações entre seus membros.
Todas as características fisicamente conseqüentes dos comportamentos dos sistemas mecânicos quânticos são conseqüências das propriedades matemáticas dessas relações, e as mais importantes delas são easilysummarized:
(P1)
Uma forma de adicionar vetores num espaço Hilbert ormultiplicando-os por escalares irá produzir um vetor que também está no espaço. Caso o vetor seja normalizado, ele, a partir de (3.1), representará um possível estado do sistema, e caso seja a soma de um par de vetores próprios de um observável com valores próprios distintos, ele não será ele mesmo um vetor próprio de (B), mas será associado, a partir de (3.4b), com um conjunto de probabilidades de mostrar um outro resultado em medições.
(P2)
Para qualquer operador hermitiano num espaço Hilbert, existem outros, no mesmo espaço, com os quais não partilha um conjunto completo de vectores próprios; de facto, é fácil mostrar que existem outros aspiradores com os quais não tem vectores próprios em comum.
Se fizermos algumas suposições interpretativas adicionais, podemos dizer mais. Suponha, por exemplo, que
(4.1)
Cada operador hermitiano no espaço Hilbert associado a um sistema representa um distinto observável, e (portanto)cada vector normalizado, um estado distinto, e
(4.2)
Um sistema tem um valor para observável se, e apenas se, o vector que representa o seu estado for um estado eigenstate do operador \i(A\i). O valor que ele tem, em tal caso, é apenas o valor próprio associado com aquele estado eigenstate.
Segundo (P2), por (3.1), que nenhum estado mecânico quântico é aneigenstate de todos os observáveis (e de fato há observáveis que não têm eigenstatos em comum), e assim, por (3.2), que nenhum sistema mecânico quântico tem valores simultâneos para todas as quantidades pertencentes a ele (e, de fato, que há pares de quantidades aos quais nenhum estado atribui valores simultâneos).
Existem operadores hermitianos no produto tensor\(H_1 {\i1}ovezes H_2} de um par de espaços Hilbert\i}(H_1}) e {\i}(H_2}) … No caso de H_1 e H_2 serem os espaços de estado dos sistemas S1 e S2, H_1 e H_2 é o espaço de estado do sistema complexo S1+S2. Daí resulta (4.1) que existem observáveis pertencentes a \((S1+S2)\) cujos valores não são determinados pelos valores dos observáveis pertencentes aos dois individualmente.
Estas são todas consequências directas de tomar vectores e operadores no espaço de Hilbert para representar, respectivamente, estados e observáveis, e aplicar a Regra de Born (e mais tarde (4.1) e (4.2)), togando o significado empírico às atribuições de estados. Isso é perfeitamente compreendido; a dificuldade real em compreender a mecânica quântica é a de compreender as suas implicações – físicas, metafísicas e epistemológicas.
Anyone trying to come to an understanding about what quantum mechanicssaysays about the world has to grapple with one remaining fact. Este problema não é um problema dos espaços de Hilbert, mas das dinâmicas – as regras que descrevem as trajectórias que os sistemas seguem através do espaço. Do ponto de vista físico, é muito mais moreworrisome do que qualquer coisa discutida até este ponto. Não só apresenta dificuldades para alguém tentando fornecer uma interpretação da teoria, mas também parece apontar para uma inconsistência lógica nos fundamentos da teoria.
Suponha que temos um sistema e um dispositivo que mede o anobservável (A) com valores Depois, há um testamento de (S^*) (o ‘estado do solo’), e alguns observáveis (B) com valores (b_1, b_2, b_3, …\(o seu ‘ponteiro observável’, assim chamado porque é o que quer que desempenhe o papel do ponteiro num mostrador na frente de um instrumento de medição esquemático que regista o resultado da experiência), e se o valor de A imediatamente antes da interação for de a_1, então o valor de B imediatamente depois é de b_1. Se, no entanto, o valor de A imediatamente antes da interação for a_2, então o valor de B imediatamente depois é b_2; se o valor de A imediatamente antes da interação for a_3, então o valor de B imediatamente depois é b_3, e assim por diante. É isso mesmo que significa dizer que mede. Portanto, se representarmos o estado conjunto, parcial do (S) e (S^**) (apenas a parte que especifica o valor de , o observável cujos valores correspondem a atribuições conjuntas de valores ao observável medido no (S) e o ponteiro observável no (S^**)) pelo vetor (A=a_i}_s (B=b_i}_s), e deixemos que o “righttarrow” se oponha à descrição dinâmica da interação entre os dois, para dizer que o S^* é um instrumento de medição para o A é dizer que as leis dinâmicas implicam que,
e assim por diante.
Intuitivamente, o S é um instrumento de medida para um observável, apenas porque existe uma característica observável do S (não importa o quê, apenas algo cujos valores podem ser determinados olhando para o dispositivo), que está correlacionado com os valores dos sistemas nele introduzidos de tal forma que podemos ler esses valores dos observáveis do S após a interação. Em linguagem filosófica, é um instrumento de ameaquecimento para o caso de haver alguma característica observável que siga ou indique os valores dos sistemas com os quais interage de forma apropriada.
Agora, segue-se de (3.1), acima, que existem estados de (toomany a contar) que não são autoestados de (A), e se considerarmos o que a equação de Schrödinger nos diz sobre a evolução conjunta de (S) e (S^*) quando é iniciada em um destes, descobrimos que o estado do par após interação é uma sobreposição de autoestados de (A). Não importa o que é observável no que está a ser medido, e não importa em que superposição em particular começa; quando é introduzido num instrumento de medição para aquele observável, se a interacção é correctamente descrita pela sequência de Schrödinger, decorre apenas da linearidade do U naquela equação, o operador que efectua a transformação do estado anterior para o estado posterior do par, que o estado conjunto do S e o aparelho após a interacção é uma sobreposição de autoestados deste observável sobre o sistema conjunto.
Ponha, por exemplo, que nós começamos ^**) no seu estado de terra, e ^(S^*) no estado
É uma consequência das regras para obter o estado-espaço do sistema composto que o estado combinado do par é
e decorre do facto de que ^*) é um instrumento de medida para ^(A),e a linearidade de que o seu estado combinado após a interacção, é
Isto, no entanto, é inconsistente com a regra dinâmica para contextos de tipo 2, para a regra dinâmica para contextos de tipo 2 (e se houver algum desses contextos, este é um) implica que o estado do par após interação é ou
\i
ou
\i
Indeed, implica que há uma probabilidade precisa de que acabará na primeira e uma probabilidade de que acabará na segunda.
Podemos tentar restaurar a consistência lógica, renunciando à regra dinâmica para contextos do tipo 2 (ou, o que equivale à mesma coisa, desistindo de que existem tais contextos), mas então temos o problema da consistência com a experiência. Pois não foi um mero erro que essa regra tenha sido incluída na teoria; sabemos como é o asistema quando está num estado inicial de um dado observável, e sabemos, olhando para o aparelho de medida, que o pós-medição está num estado inicial do ponteiro observável. E assim sabemos desde o início que se uma teoria nos diz algo mais sobre os estados pós-medição dos aparelhos de medição, qualquer que seja essa outra coisa, ela está errada.
Que, em resumo, é o Problema da Medição na Mecânica Quântica; qualquer interpretação da teoria, qualquer história detalhada sobre como é o mundo de acordo com a mecânica quântica, e em particular aqueles pedaços do mundo em que as medições estão acontecendo, tem que lutar com ela.
Loose Ends
Os estados mistos são somas ponderadas de estados puros, e podem ser usados para representar os estados de conjuntos cujos componentes estão em diferentes estados puros, ou estados de sistemas individuais sobre os quais temos apenas um conhecimento parcial. No primeiro caso, o peso atribuído a um dado estado puro reflete o tamanho do componente do conjunto que está nesse estado (e, portanto, a objetividade que é um membro arbitrário do conjunto); no segundo caso, eles refletem a probabilidade epistêmica de que o sistema inquestionável ao qual o estado é atribuído esteja nesse estado.
Se não queremos perder a distinção entre estados puros e mistos, precisamos de uma forma de representar a soma ponderada de um conjunto de purestados (equivalentemente, das funções de probabilidade associadas a eles) que seja diferente da adição do vector (devidamente ponderado) que os representa, e isso significa que precisamos ou de uma forma alternativa de representar estados mistos, ou uma forma uniforme de representar tanto os estados puros como os mistos que preserve a distinção entre eles.Há uma espécie de operador nos espaços de Hilbert, chamado operador de densidade, que serve bem nesta última capacidade, e acaba por não ser difícil reafirmar tudo o que foi dito sobre os vectores de densidade em termos de operadores de densidade. Assim, ainda que seja comum falar como se os estados puros fossem representados por vetores, a regra oficial é que os estados – puros e mistos, igualmente – arerepresentados na mecânica quântica pelos operadores de densidade.
Embora os estados mistos possam, como eu disse, ser usados para representar a ignorância dos estados dos sistemas que estão realmente num outro estado puro, e embora esta tenha parecido a muitos ser uma forma adequada de interpretar misturas em contextos clássicos, existem sérios obstáculos à sua aplicação em geral a misturas mecânicas quânticas. Estes são deixados para discussão detalhada nos outros verbetes sobre mecânica quântica da Enciclopédia.
Muito do que foi dito sobre os observáveis, estritamente falando, aplica-se apenas ao caso em que os valores da forma observável são definidos de forma adiscreta; os simpatias matemáticas necessárias para generalizar o caso dos observáveis contínuos são complicados, e levantam problemas de natureza mais técnica. Estes também são melhor deixados para uma discussão detalhada.
Esta deve ser toda a preparação inicial que se precisa para abordar a discussão filosófica da mecânica quântica, mas é apenas um primeiro passo. Quanto mais se aprende sobre as relações entre e entre vetores e operadores no espaço Hilbert, sobre como os espaços de sistemas simples se relacionam com os de sistemas complexos, e sobre a equação que descreve como os vetores de estado se movem através do espaço, melhor será a apreciação tanto da natureza quanto da dificuldade dos problemas associados à teoria. O engraçado de trás para a frente da mecânica quântica, o que faz com que ela seja sem dúvida absorvida por um filósofo, é que quanto mais se aprende, mais duros ficam os problemas.