Mechanika kwantowa
Terminologia
Układy fizyczne dzielą się na typy zgodnie z ich niezmiennymi (lub 'niezależnymi od stanu’) własnościami, a stan układu w czasie składa się z kompletnej specyfikacji tych jego własności, które zmieniają się w czasie (jego własności 'zależne od stanu’). Aby dać kompletny opis systemu, musimy powiedzieć, jakiego typu jest to system i jaki jest jego stan w każdym momencie jego historii.
Wielkość fizyczna jest wzajemnie wykluczającą się i łącznie wyczerpującą się rodziną własności fizycznych (dla tych, którzy znają ten sposób mówienia, jest to rodzina własności o strukturze komórek w partycji). Wiedza o tym, jakie wartości przyjmuje dana wielkość, może nam wiele powiedzieć o relacjach między własnościami, z których się ona składa. Wartości wielkości dwuwartościowej, na przykład, tworzą zbiór o dwóch członach; wartości wielkości rzeczywistej tworzą zbiór o strukturze liczb rzeczywistych. Jest to szczególny przypadek czegoś, o czym będziemy się jeszcze wielokrotnie przekonywać, a mianowicie,że wiedza o tym, jakiego rodzaju obiekty matematyczne reprezentują elementy jakiegoś zbioru (tutaj, wartości wielkości fizycznej; później, stany, jakie może przyjąć system lub wielkości odnoszące się do niego) mówi nam bardzo wiele (w rzeczy samej, prawdopodobnie wszystko, co można wiedzieć) o relacjach między nimi.
W kontekstach mechaniki kwantowej termin „obserwowalny” jest używany zamiennie z terminem „wielkość fizyczna” i powinien być traktowany jako termin techniczny o tym samym znaczeniu. Nie jest przypadkiem, że pierwsi twórcy teorii wybrali ten termin, ale wybór ten został dokonany z powodów, które obecnie nie są powszechnie akceptowane. Przestrzeń stanów układu to przestrzeń utworzona przez zbiór jego możliwych stanów, tj. fizycznie możliwych sposobów połączenia wartości wielkości charakteryzujących go wewnętrznie. W teoriach klasycznych zbiór wielkości, który stanowi podstawę superweniencji dla pozostałych, jest zwykle określany jako „podstawowy” lub „fundamentalny”, a ponieważ każdy matematycznie możliwy sposób połączenia ich wartości jest fizyczną możliwością, przestrzeń stanów można uzyskać, po prostu biorąc je za współrzędne. Tak więc, na przykład, przestrzeń stanów klasycznego układu mechanicznego złożonego z ∗ cząstek, uzyskana przez określenie wartości ∗ 6n wartości rzeczywistych wielkości – trzech składowych położenia i trzech pędu dla każdej cząstki w układzie – stanowi ∗ 6n wymiarową przestrzeń współrzędnych. Każdy możliwy stan takiego układu odpowiada punktowi w tej przestrzeni, a każdy punkt w przestrzeni odpowiada możliwemu stanowi takiego układu. Sytuacja wygląda nieco inaczej w mechanice kwantowej, gdzie istnieją matematycznie opisywalne sposoby łączenia wartości wielkości, które nie reprezentują fizycznie możliwych stanów. Jak zobaczymy, przestrzenie stanów mechaniki kwantowej są specjalnymi rodzajami przestrzeni wektorowych, zwanych przestrzeniami Hilberta, i mają więcej wewnętrznej struktury niż ich klasyczne odpowiedniki.
Struktura jest zbiorem elementów, na których określone są pewne operacje i relacje, struktura matematyczna jest po prostu strukturą, w której elementy są obiektami matematycznymi (liczbami, zbiorami, wektorami), a operacje matematyczne, a model jest strukturą matematyczną używaną do reprezentowania jakiejś fizycznie istotnej struktury w świecie.
Serce i dusza mechaniki kwantowej zawarte są w przestrzeniach Hilberta, które reprezentują przestrzenie stanów układów kwantowo-mechanicznych. Wewnętrzne relacje pomiędzy stanami i wielkościami oraz wszystko, co z tego wynika dla sposobów zachowania się układów kwantowo-mechanicznych, są wplecione w strukturę tych przestrzeni, ucieleśnione w relacjach pomiędzy obiektami matematycznymi, które je reprezentują. Oznacza to, że zrozumienie, jak wygląda układ zgodnie z mechaniką kwantową, jest nierozerwalnie związane ze znajomością wewnętrznej struktury tych przestrzeni. Jeśli poznasz przestrzeń Hilberta i prawa dynamiki opisujące drogę wektorów w tej przestrzeni, będziesz wiedział wszystko, co można wiedzieć o systemach opisywanych przez tę teorię, zgodnie z jej założeniami.
Mówiąc o 'znajomości przestrzeni Hilberta’ mam na myśli coś więcej niż tylko posiadanie jej opisu lub mapy; każdy, kto ma na półce podręcznik mechaniki kwantowej, ma coś takiego. Mam na myśli umiejętność poruszania się po niej w taki sposób, w jaki poruszamy się po mieście, w którym mieszkamy. Jest to praktyczny rodzaj wiedzy, która przychodzi stopniowo i najlepiej nabyć ją ucząc się rozwiązywać problemy tego typu: Jak dostać się z punktu A do punktu B? Czy mogę się tam dostać nie przejeżdżając przez C? I jaka jest najkrótsza droga? Studenci fizyki spędzają długie lata na poznawaniu zakamarków przestrzeni Hilberta, lokalizowaniu znajomych punktów orientacyjnych, chodzeniu utartymi ścieżkami, uczeniu się, gdzie leżą tajne przejścia i ślepe zaułki, oraz rozwijaniu poczucia ogólnego układu terenu. Uczą się, jak poruszać się po przestrzeni Hilberta w sposób, w jaki taksówkarz uczy się poruszać po swoim mieście.
Ile tego rodzaju wiedzy potrzeba, by podejść do problemów filozoficznych związanych z teorią? Na początku niezbyt wiele: tylko najbardziej ogólne fakty dotyczące geometrii krajobrazu (który w każdym razie, w przeciwieństwie do większości miast, jest pięknie zorganizowany) oraz dróg, jakimi poruszają się po nim układy (wektory reprezentujące stany). To właśnie zostanie tutaj wprowadzone: najpierw trochę łatwej matematyki, a potem, w skrócie, teoria.
Matematyka
2.1 Wektory i przestrzenie wektorowe
Wektor \(A\), zapisywany jako \(\), jest obiektem matematycznym charakteryzującym się długością, \(\), i kierunkiem. Wektor znormalizowany jest wektorem o długości 1, tzn. \(|A| = 1\). Wektory można dodawać do siebie, mnożyć przez stałe (w tym liczby zespolone) i mnożyć razem. Dodawanie wektorów odwzorowuje dowolną parę wektorów na inny wektor, w szczególności ten, który otrzymujemy przesuwając drugi wektor tak, by jego ogon pokrywał się z wierzchołkiem pierwszego, bez zmiany długości ani kierunku żadnego z nich, a następnie łącząc ogon pierwszego z wierzchołkiem drugiego. Ta reguła dodawania znana jest jako prawo równoległoboku. Tak więc, na przykład, dodanie wektorów \(\ket{A}) i \(\ket{B}) daje wektor \(\ket{C}) (= \ket{A} + \ket{B})\) jak na Rysunku 1:
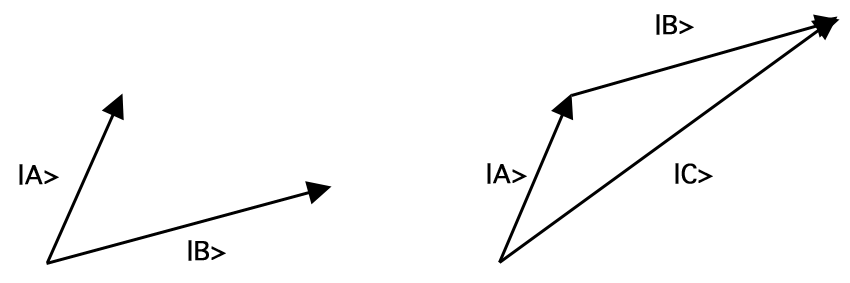
Rysunek 1.Dodawanie wektorów
Mnożąc wektor ∗ przez ∗, gdzie ∗ jest stałą, otrzymujemy wektor, który ma ten sam kierunek co ∗, ale którego długość jest ∗ razy dłuższa od długości ∗.
W rzeczywistej przestrzeni wektorowej iloczyn (wewnętrzny lub punktowy) pary wektorów \(\ket{A}} i \(\ket{B}}), zapisany jako \(\braket{A}{B}}}, jest skalarem równym iloczynowi ich długości (lub „norm”) pomnożonemu przez cosinus kąta między nimi:
Niech \(\ket{A_1}) i \(\ket{A_2}) będą wektorami o długości 1 („wektory jednostkowe”) takimi, że \(\braket{A_1}{A_2} = 0\). (Kąt między tymi dwoma wektorami jednostkowymi musi wynosić 90 stopni.) Wtedy możemy przedstawić dowolny dwuwymiarowy wektor \(\ket{B}) za pomocą naszych wektorów jednostkowych w następujący sposób:
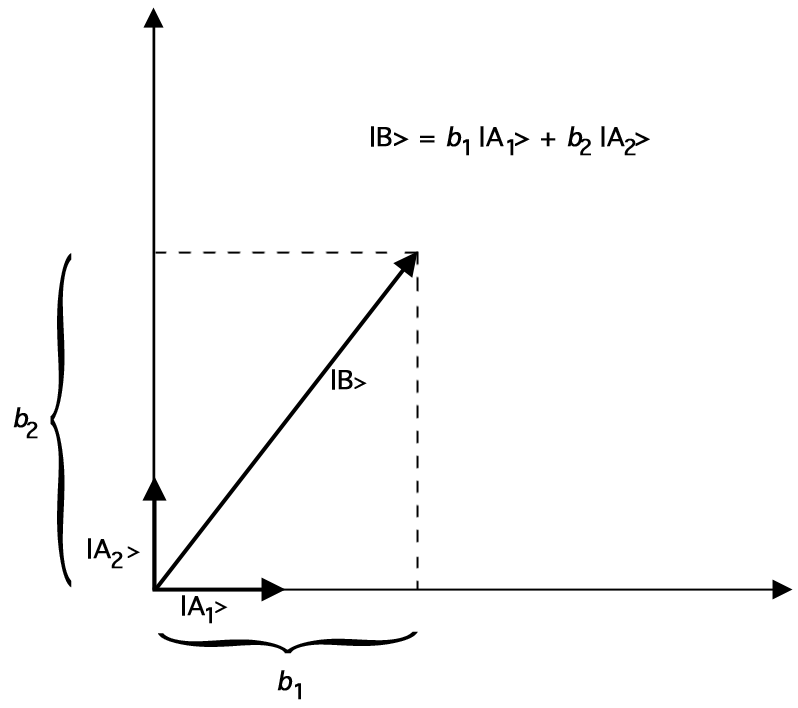
Rysunek 2.Reprezentacja iloczynu wewnętrznego przez dodawanie wektorów jednostkowych
Teraz definicję iloczynu wewnętrznego należy zmodyfikować tak, aby miała zastosowanie do przestrzeni złożonych. Niech \(c^*\) będzie złożoną koniugacją \(c\). (Gdy c^* jest liczbą zespoloną postaci \(a \pm bi \), to sprzężenie zespolone c^* \ jest zdefiniowane następująco:
\^* = a-bi \ = a+bi \]
Tak więc, dla wszystkich liczb zespolonych \(c), \(^* = c\), ale \(c^* = c\) tylko w przypadku, gdy \(c\) jest rzeczywista). Teraz definicję iloczynu wewnętrznego \(\ket{A}) i \(\ket{B}) dla przestrzeni zespolonych można podać w postaci koniugatów współczynników zespolonych w następujący sposób. Gdzie \(\ket{A_1}} i \(\ket{A_2}} są opisanymi wcześniej wektorami jednostkowymi, \(\ket{A} = a_1 \ket{A_1} + a_2 \ket{A_2}}) i \(\ket{B} = b_1 \ket{A_1} + b_2 \ket{A_2}}), wtedy
Najbardziej ogólne i abstrakcyjne pojęcie iloczynu wewnętrznego, którego dwa szczególne przypadki teraz zdefiniowaliśmy, jest następujące. \(\braket{A}{B}\) jest iloczynem wewnętrznym na przestrzeni wektorowej \(\) tylko w przypadku
- \(\braket{A}{A} = |A|^2\), i \(\braket{A}{A}=0\) wtedy i tylko wtedy, gdy \(A=0\)
- \(\braket{B}{A} = \braket{A}{B}^*\)
- \(\braket{B}{A+C}= \braket{B}{A} + \braket{B}{C}\).
Wynika z tego, że
- długość \(\) jest pierwiastkiem kwadratowym iloczynu wewnętrznego \(\ket{A}) z samym sobą, tzn,\(\ket{A}} i \(\ket{B}} są wzajemnie prostopadłe lub prostopadłe wtedy i tylko wtedy, gdy \(\braket{A}{B}}}.
Przestrzeń wektorowa to zbiór wektorów zamkniętych na dodawanie i mnożenie przez stałe, przestrzeń iloczynu wewnętrznego to przestrzeń wektorowa, na której zdefiniowano operację mnożenia wektorów, a wymiar takiej przestrzeni to maksymalna liczba niezerowych, wzajemnie ortogonalnych wektorów, które zawiera.
Dowolny zbiór wektorów wzajemnie ortogonalnych o długości 1 w przestrzeni wektorowej pewnego wymiaru stanowi bazę ortonormalną tej przestrzeni. Niech \(\ket{A_1}, \ldots, \ket{A_N}) będzie takim zbiorem wektorów jednostkowych. Wówczas każdy wektor w tej przestrzeni można wyrazić jako sumę postaci:
gdzie b_i = \braket{B}{A_i}}. Współczynniki b_i są tu znane jako współczynniki rozwinięcia B w bazie A.
Zauważ, że:
- dla wszystkich wektorów \(A\), \(B\) i \(C\) w danej przestrzeni,\i>
- dla dowolnych wektorów \(M\) i \(Q\), wyrażonych w bazie \(A\),
i
\\
Istnieje jeszcze jeden sposób zapisu wektorów, a mianowicie zapis współczynników rozwinięcia (względem danej bazy) w kolumnie, np:
gdzie q_i = \braket{Q}{A_i} \), a \a_i> są wybranymi wektorami bazowymi.
Gdy mamy do czynienia z przestrzeniami wektorowymi o nieskończonych wymiarach, ponieważ nie możemy zapisać całej kolumny współczynników rozwinięcia potrzebnej do wypisania wektora, gdyż musiałaby ona być nieskończenie długa, więc zamiast tego zapisujemy funkcję (zwaną „funkcją falową” dla q_i, zwykle przedstawianą w postaci \(\psi(i))\), która ma te współczynniki jako wartości. Zapisujemy, czyli funkcję:
Mając dowolny wektor w przestrzeni wektorowej i dowolną podstawę dla tej przestrzeni, możemy otrzymać funkcję falową wektora w tej podstawie; a mając funkcję falową wektora w danej podstawie, możemy skonstruować wektor, którego funkcją falową jest ten wektor. Ponieważ okazuje się, że większość ważnych operacji na wektorach odpowiada prostym operacjom algebraicznym na ich funkcjach falowych, jest to zwykły sposób reprezentowania wektorów państwowych.
Gdy para układów fizycznych oddziałuje na siebie, tworzą one układ złożony, a w mechanice kwantowej, podobnie jak w mechanice klasycznej, istnieje reguła konstruowania przestrzeni stanów układu złożonego z przestrzeni jego składników, reguła, która mówi nam, jak uzyskać z przestrzeni stanów, \(H_A \) i \(H_B \) dla \(A \) i \(B \), odpowiednio, przestrzeń stanów – zwana 'tensorproduktem’ \(H_A \) i \(H_B \), i zapisana \(H_A \otimes H_B \) – pary. W szczególności okazuje się, że stan systemu złożonego nie jest jednoznacznie określony przez stan jego części składowych. Oznacza to, a przynajmniej tak się wydaje, że zgodnie z mechaniką kwantową istnieją fakty dotyczące układów złożonych (a nie tylko fakty dotyczące ich konfiguracji przestrzennej), które nie są nadrzędne wobec faktów dotyczących ich składników; oznacza to, że istnieją fakty dotyczące układów jako całości, które nie są nadrzędne wobec faktów dotyczących ich części i sposobu, w jaki te części są rozmieszczone w przestrzeni. Znaczenia tej cechy teorii nie da się przecenić; jest ona, w taki czy inny sposób, uwikłana w większość najtrudniejszych problemów.
Nieco bardziej szczegółowo: jeśli \(v_{i}^A \) jest ortonormalną podstawą dla \(H_A \), a \(\u_{j}^B \) jest ortonormalną podstawą dla \(H_B \), to zbiór par \((v_{i}^A, u_{j}^B)\) jest przyjmowany jako tworzący ortonormalną podstawę dla przestrzeni iloczynu tensorowego \(H_A \times H_B \). Dla pary \(v_i^A \otimes u_j^B \) stosuje się oznaczenie \((v_{i}^A,u_{j}^B)\), a iloczyn wewnętrzny na \(H_A \otimes H_B \) definiuje się jako:
Z konstrukcji tej wynika, że choć każdy wektor w przestrzeni H_A ^A ^A ^B jest sumą liniową wektorów wyrażalnych w postaci
- , to nie każdy wektor w tej przestrzeni jest sam wyrażalny w tej postaci i okazuje się, że
- każdy stan zespolony definiuje jednoznacznie stany swoich składowych.
- jeśli stany A i B są czyste (tzn, reprezentowalne przez wektory odpowiednio v^A i u^B), to stan \(A+B)\) jest czysty i reprezentowany przez v^A i u^B, i
- jeśli stan \(A+B)\) jest czysty i wyrażalny w formie \(v^A \otimes u^B\), wtedy stany \(A\) i \(B\) są czyste, ale
- jeśli stany \(A\) i \(B\) nie są czyste, tj.e., jeśli są to stany mieszane (zdefiniowane poniżej), nie definiują one jednoznacznie stanu \(A+B)\); w szczególności, może to być stan czysty nie dający się wyrazić w postaci \(v^A \otimes u^B \).
2.2 Operatory
Operator jest odwzorowaniem przestrzeni wektorowej na nią samą; przenosi on dowolny wektor \(\ket{B}) w przestrzeni na inny wektor \(\ket{B’}) również znajdujący się w tej przestrzeni; \(O \ket{B} = \ket{B’}). Operatory liniowe to operatory, które mają następujące własności:
- O(O \ket{A} + \ket{B}) = O \ket{A} + O \ket{B}), oraz
- O(c \ket{A}) = c(O \ket{A})\).
Tak jak każdy wektor w przestrzeni \(N)-wymiarowej może być reprezentowany przez kolumnę liczb \(N), względem wyboru podstawy przestrzeni, tak każdy operator liniowy na tej przestrzeni może być reprezentowany w notacji kolumnowej przez liczby \(N^2\):
gdzie \(O_{ij} = \braket{A_i}{O \mid A_j}\) i \(A_N\) są wektorami bazowymi przestrzeni. Wpływ operatora liniowego na wektor B jest więc dany przez
Jeszcze dwie definicje, zanim będziemy mogli powiedzieć, czym są przestrzenie Hilberta, a potem możemy przejść do mechaniki kwantowej. \(\ket{B}) jest wektorem własnym \(O\) o wartości własnej \(a\) wtedy i tylko wtedy, gdy \(O \ket{B} = a \ket{B}).Różne operatory mogą mieć różne wektory własne, ale relacja wektor własny/operator zależy tylko od operatora i wektorów, o których mowa, a nie od szczególnej podstawy, w której są wyrażone; relacja wektor własny/operator jest, to znaczy, niezmienna przy zmianie podstawy. Operator hermitowski jest operatorem, który ma tę własność, że istnieje ortonormalna podstawa składająca się z jego wektorów własnych, a te wartości własne są wszystkie rzeczywiste.
Mechanika kwantowa
Cztery podstawowe zasady mechaniki kwantowej to:
(3.1)
Stany fizyczne.Każdy układ fizyczny jest związany z przestrzenią Hilberta, każdy wektor jednostkowy w tej przestrzeni odpowiada możliwemu czystemu stanowi układu,a każdy możliwy czysty stan, jakiemuś wektorowi w tej przestrzeni.
(3.2)
Ciśnie fizyczne.Operatory hermitowskie w przestrzeni Hilberta związanej z układem reprezentują wielkości fizyczne, a ich wartości własne reprezentują możliwe wyniki pomiarów tych wielkości.
Istnieje operator, zwany hamiltonianem, który odgrywa szczególną rolę w teorii kwantowej, ponieważ dynamika układu może być wygodnie sformułowana poprzez śledzenie jego ewolucji. Hamiltonian – zapisywany jako \(H\), lub \(\hat{H}) – oznacza całkowitą energię układu. Jego wartości własne są możliwymi wynikami, które można uzyskać w pomiarach energii całkowitej. Przestrzeń Hilberta związana z układem złożonym jest iloczynem tensorowym przestrzeni związanych z układami prostymi (w standardowej, nierelatywistycznej teorii: pojedynczymi cząstkami), z których się składa.
(3.4) Dynamika. a.
Konteksty typu 1: Biorąc pod uwagę stan układu w chwili (t) oraz siły i ograniczenia, którym podlega, istnieje równanie, „sekwencja Schrödingera”, które daje stan w każdej innej chwili \(Uket{v_t} \rightarrow \ket{v_{t’}}). Dla naszych celów ważne są następujące własności \(U): jest deterministyczna, co oznacza, że przekształca stan systemu w jednym czasie w niepowtarzalny stan w każdym innym czasie; jest unitarna, co oznacza, że jest automorfizmem przestrzeni Hilberta, na którą działa (tzn, odwzorowaniem tej przestrzeni na siebie, które zachowuje liniową strukturę przestrzeni i iloczyn wewnętrzny), i jest liniowy, co oznacza, że jeśli przenosi stan \(\ket{A}) na stan \(\ket{A’}), i przyjmuje stan \B}na stan \B’}, to przyjmuje dowolny stan w postaci \a \ket{A} + \beta \ket{B} na stan \a \a \A’} + \beta \ket{B’}.
Konteksty typu 2 („Konteksty pomiarowe”): Przeprowadzenie „pomiaru” obserwowalnej ∗ na układzie znajdującym się w stanie ∗ (∗ket{A}}) skutkuje rozpadem układu na stan własny odpowiadający obserwowanej wartości własnej. Jest to znane jako postulat kolapsu. Który konkretnie stan własny się zawali jest kwestią prawdopodobieństwa, a prawdopodobieństwa są określone przez regułę znaną jako Reguła Borna: Istnieją dwa ważne punkty, które należy zauważyć o tych dwóch rodzajach kontekstów:
- Rozróżnienie pomiędzy kontekstami typu 1 i 2 pozostaje do ustalenia w kategoriach mechaniki kwantowej; nikomu nie udało się powiedzieć w sposób całkowicie zadowalający, w terminach dostarczonych przez teorię, które konteksty są kontekstami pomiarowymi, i
- Nawet jeśli rozróżnienie zostanie dokonane, jest otwartym pytaniem interpretacyjnym, czy istnieją konteksty typu 2; tj.e., jest otwartym pytaniem interpretacyjnym, czy istnieją jakiekolwiek konteksty, w których systemy są rządzone przez regułę dynamiczną inną niż równanie Schrödingera.
Structures on Hilbert Space
Zauważyłem powyżej, że w ten sam sposób, w jaki wszystkie informacje, które mamy o relacjach pomiędzy miejscami w mieście są zawarte w przestrzennych relacjach pomiędzy punktami na mapie, które je reprezentują, wszystkie informacje, które mamy o wewnętrznych relacjach pomiędzy (i pomiędzy) stanami i wielkościami w mechanice kwantowej są zawarte w matematycznych relacjach pomiędzy wektorami i operatorami, które je reprezentują. Z matematycznego punktu widzenia, to co naprawdę odróżnia mechanikę kwantową od jej klasycznych poprzedników to fakt, że stany i wielkości mają bogatszą strukturę; tworzą one rodziny z bardziej interesującą siecią relacji pomiędzy ich członkami.
Wszystkie fizycznie istotne cechy zachowań układów mechaniki kwantowej są konsekwencjami matematycznych własności tych relacji, a najważniejsze z nich można łatwo podsumować następująco:
(P1)
Każdy sposób dodawania wektorów w przestrzeni Hilberta lub mnożenia ich przez skalary da wektor, który również znajduje się w tej przestrzeni. W przypadku, gdy wektor jest znormalizowany, będzie on, z (3.1), reprezentował możliwy stan układu, a w przypadku, gdy będzie sumą pary wektorów własnych obserwowalnego ∗ z różnymi wartościami własnymi, sam nie będzie wektorem własnym ∗, ale będzie związany, z (3.4b), ze zbiorem prawdopodobieństw pokazania takiego lub innego wyniku w pomiarach ∗.
(P2)
Dla dowolnego operatora hermitowskiego na przestrzeni Hilberta istnieją inne, na tej samej przestrzeni, z którymi nie ma on wspólnego pełnego zestawu wektorów własnych; w rzeczy samej, łatwo pokazać, że istnieją inne takie operatory, z którymi nie ma on wspólnych wektorów własnych.
Jeśli przyjmiemy kilka dodatkowych założeń interpretacyjnych, możemy powiedzieć więcej. Przyjmijmy na przykład, że
(4.1)
Każdy operator hermitowski na przestrzeni Hilberta związany z układem reprezentuje odrębną obserwowalną i (stąd) każdy znormalizowany wektor, odrębny stan i
(4.2)
Układ ma wartość dla obserwowalnej ∗ wtedy i tylko wtedy, gdy wektor reprezentujący jego stan jest stanem własnym operatora ∗. Wartość, którą ma w takim przypadku, jest po prostu wartością własną związaną z tym stanem własnym.
Z (P2), z (3.1) wynika, że żaden stan mechaniki kwantowej nie jest stanem własnym wszystkich obserwabli (i rzeczywiście, że istnieją obserwable, które nie mają wspólnych stanów własnych), a więc, z (3.2), że żaden układ mechaniki kwantowej nigdy nie ma równoczesnych wartości dla wszystkich wielkości w nim występujących (i rzeczywiście, że istnieją pary wielkości, którym żaden stan nie przypisuje równoczesnych wartości).
Istnieją operatory hermitowskie na iloczynie tensorowym (H_1 ∗ razy H_2 ∗) pary przestrzeni Hilberta (H_1 ∗) i (H_2 ∗) … W przypadku, gdy H_1 i H_2 są przestrzeniami stanów systemów S1 i S2, to H_1 jest przestrzenią stanów systemu złożonego ((S1+S2)\). Z tego wynika, na podstawie (4.1), że istnieją obserwable odnoszące się do układu ((S1+S2)\), których wartości nie są zdeterminowane przez wartości obserwabli odnoszących się do tych dwóch układów indywidualnie.
Wszystko to jest prostą konsekwencją przyjęcia wektorów i operatorów w przestrzeni Hilberta jako reprezentantów, odpowiednio, stanów i obserwabli, oraz zastosowania Reguły Borna (i późniejszych (4.1) i (4.2)), aby nadać empiryczne znaczenie przypisaniom stanów. To wszystko jest doskonale zrozumiałe; prawdziwa trudność w zrozumieniu mechaniki kwantowej polega na uporaniu się z jej implikacjami – fizycznymi, metafizycznymi i epistemologicznymi.
Każdy, kto stara się zrozumieć, co mechanika kwantowa mówi o świecie, musi zmierzyć się z jednym faktem. Problem ten nie dotyczy przestrzeni Hilberta, ale dynamiki – reguł opisujących trajektorie, którymi układy podążają przez przestrzeń. Z fizycznego punktu widzenia jest on o wiele bardziej niepokojący niż wszystko, co do tej pory omówiono. Nie tylko stanowi trudność dla kogoś, kto próbuje zinterpretować teorię, ale także wydaje się wskazywać na logiczną niespójność w jej podstawach.
Załóżmy, że mamy system \(S) i urządzenie \(S^*\), które mierzy obserwowalną \(A\) na \(S) o wartościach \(\{a_1,a_2, a_3, …\). Następnie istnieje pewien stan ^* („stan podstawowy”) i pewien obserwowalny \(B\) o wartościach \(\b_1, b_2,b_3, …\(„obserwowalne wskazujące”, nazwane tak, ponieważ odgrywają rolę wskazówki na tarczy schematycznego przyrządu pomiarowego, rejestrującej wynik eksperymentu), które są takie, że jeżeli ∗ rozpoczyna się w stanie podstawowym i oddziałuje w odpowiedni sposób z ∗, i jeżeli wartość ∗ bezpośrednio przed oddziaływaniem wynosi ∗ a_1, to wartość ∗ bezpośrednio po nim wynosi ∗ b_1. To właśnie oznacza, że ∗ (S^*) jest miarą ∗ (A). Jeśli więc przedstawimy wspólny, częściowy stan \(S) i \(S^*} (tylko tę jego część, która określa wartość obserwowalnego, którego wartości odpowiadają wspólnym przypisaniom wartości do mierzonego obserwowalnego na \(S) i obserwowalnego wskaźnikowego na \(S^*}) za pomocą wektora \(\ket{A=a_i}_s \ket{B=b_i}_{s^*}), i niech „\”\”oznacza dynamiczny opis interakcji między nimi, aby powiedzieć, że \”S^*\” jest instrumentem pomiarowym dla \”A\”, to powiedzieć, że prawa dynamiczne pociągają za sobą, że,
\”\”\”\” i tak dalej.
Intuicyjnie, ^* jest instrumentem pomiarowym dla obserwowalnego ^* tylko wtedy, gdy istnieje jakaś obserwowalna cecha ^* (nie ma znaczenia jaka, po prostu coś, czego wartości można stwierdzić patrząc na urządzenie), która jest skorelowana z wartościami ^* systemów wprowadzanych do niego w taki sposób, że możemy odczytać te wartości z obserwowalnego stanu ^* (S^*) po interakcji. W języku filozoficznym, S^* jest instrumentem pomiarowym dla ^A na wypadek, gdyby istniała jakaś obserwowalna cecha S^*, która śledzi lub wskazuje wartości ^A systemów, z którymi wchodzi w interakcję w odpowiedni sposób.
Załóżmy na przykład, że rozpoczynamy oddziaływanie ^* w stanie podstawowym, a ^* w stanie
Z reguł otrzymywania przestrzeni stanów układu złożonego wynika, że połączony stan pary wynosi
i wynika z tego, że ^* jest przyrządem pomiarowym dla ^*,i liniowości U, że ich połączony stan po interakcji wynosi
To jednak, jest sprzeczne z regułą dynamiczną dla kontekstów typu 2, ponieważ reguła dynamiczna dla kontekstów typu 2 (a jeśli istnieją takie konteksty, to jest to jeden z nich) zakłada, że stan pary po interakcji jest albo
albo
albo albo
, wiąże się to z tym, że istnieje dokładne prawdopodobieństwo \(\frac{1}{2}}), że skończy w pierwszym, oraz prawdopodobieństwo \(\frac{1}{2}}), że skończy w drugim.
Możemy spróbować przywrócić logiczną spójność rezygnując z dynamicznej reguły dla kontekstów typu 2 (lub, co sprowadza się do tego samego, zaprzeczając, że istnieją jakiekolwiek takie konteksty), ale wtedy pojawia się problem spójności z doświadczeniem. Wiemy, jak wygląda układ, który znajduje się w stanie własnym danej obserwowalnej, i wiemy z doświadczenia, że aparat pomiarowy po pomiarze znajduje się w stanie własnym obserwowalnej wskaźnikowej. I tak wiemy od początku, że jeśli teoria mówi nam coś innego o stanach post-pomiarowych aparatury pomiarowej, czymkolwiek to coś innego jest, jest błędna.
To, w skrócie, jest Problem Pomiaru w mechanice kwantowej; każda interpretacja teorii, każda szczegółowa opowieść o tym, jak wygląda świat zgodnie z mechaniką kwantową, a w szczególności te kawałki świata, w których odbywają się pomiary, musi się z nim zmagać.
Luźne zakończenia
Stany mieszane są ważonymi sumami stanów czystych i mogą być używane do reprezentowania stanów zespołów, których składniki znajdują się w różnych stanach czystych, lub stanów pojedynczych układów, o których mamy tylko częściową wiedzę. W pierwszym przypadku waga przypisana do danego stanu czystego odzwierciedla wielkość składnika zespołu, który jest w tym stanie (a więc obiektywne prawdopodobieństwo, że dowolny członek zespołu jest w tym stanie); w drugim przypadku odzwierciedla ona epistemiczne prawdopodobieństwo, że system, któremu przypisany jest dany stan, jest w tym stanie.
Jeżeli nie chcemy utracić rozróżnienia pomiędzy stanami czystymi i mieszanymi, potrzebujemy sposobu reprezentacji sumy ważonej zbioru stanów czystych (równoważnie, funkcji prawdopodobieństwa z nimi związanych), który różni się od dodawania (odpowiednio ważonych) wektorów, które je reprezentują, a to oznacza, że potrzebujemy albo alternatywnego sposobu reprezentacji stanów mieszanych, albo jednolitego sposobu reprezentacji zarówno stanów czystych, jak i mieszanych, który zachowuje rozróżnienie pomiędzy nimi.Istnieje pewien rodzaj operatora w przestrzeniach Hilberta, zwany operatorem gęstości, który dobrze sprawdza się w tej drugiej roli, i okazuje się, że nie jest trudno zrekapitulować wszystko, co zostało powiedziane o wektorach stanów w kategoriach operatorów gęstości. Tak więc, chociaż zwykło się mówić, że czyste stany są reprezentowane przez wektory, oficjalną zasadą jest, że stany – zarówno czyste jak i mieszane – są reprezentowane w mechanice kwantowej przez operatory gęstości.
Ale stany mieszane mogą, jak już mówiłem, być użyte do reprezentowania naszej niewiedzy o stanach układów, które w rzeczywistości są w jednym lub drugim stanie czystym, i chociaż wielu osobom wydawało się to odpowiednim sposobem interpretacji mieszanin w kontekście klasycznym, istnieją poważne przeszkody w stosowaniu tej metody ogólnie do mieszanin kwantowo-mechanicznych. Wszystko, co zostało powiedziane na temat obserwabli, ściśle mówiąc, odnosi się tylko do przypadku, w którym wartości obserwabli tworzą zbiór dyskretny; matematyczne niuanse, które są potrzebne do uogólnienia tego do przypadku obserwabli ciągłych są skomplikowane i podnoszą problemy bardziej technicznej natury. Te również najlepiej pozostawić do szczegółowej dyskusji.
To powinno być całe wstępne przygotowanie, jakiego potrzeba, aby podejść do filozoficznej dyskusji na temat mechaniki kwantowej, ale jest to tylko pierwszy krok. Im więcej człowiek dowie się o związkach między wektorami i operatorami w przestrzeni Hilberta, o tym, jak przestrzenie prostych układów odnoszą się do przestrzeni układów złożonych oraz o równaniu, które opisuje, jak wektory stanu poruszają się w przestrzeni, tym lepiej będzie oceniał zarówno naturę, jak i trudność problemów związanych z tą teorią. Zabawna, odwrotna rzecz w mechanice kwantowej, rzecz, która sprawia, że jest ona bezgranicznie absorbująca dla filozofa, polega na tym, że im więcej się dowiadujemy, tym trudniejsze stają się problemy.
.