Em cálculo de uma única variável, as funções que se encontram são funções de uma variável (geralmente x) ou t) que varia ao longo de algum subconjunto da linha de número real (que nós denotemos por matebbb{R}). Para tal função, digamos, {(y = f(x)}), o {textobf{gráfico} da função {f} consiste nos pontos {(x, y) = (x, f(x))}. Estes pontos encontram-se no sistema de coordenadas Euclidean, que, no sistema de coordenadas Cartesiano ou rectangular, consiste em todos os pares de números reais ordenados. Utilizamos a palavra “Euclidiano” para designar um sistema no qual todas as regras habituais da geometria euclidiana se mantêm. Denotamos o plano euclidiano por “2”; o “2” representa o número de dimensões do plano. O plano euclidiano tem dois eixos perpendiculares: o eixo {x)-exo e o eixo {y)-exo.

No cálculo vectorial (ou multivariável), vamos lidar com funções de duas ou três variáveis (normalmente {x, y} ou {x, y, z}, respectivamente). O gráfico de uma função de duas variáveis, digamos, \(z = f(x,y)\), encontra-se no espaço euclidiano, que no sistema de coordenadas cartesianas consiste em todos os triplos ordenados de números reais \((a, b, c)\). Como o espaço euclidiano é tridimensional, nós o denotamos por O gráfico de f(f) consiste nos pontos {\i(x, y, z) = (x, y, f(x, y))}). O sistema de coordenadas tridimensionais do espaço euclidiano pode ser representado numa superfície plana, como esta página ou um quadro negro, apenas dando a ilusão de três dimensões, da forma mostrada na Figura 1.1.1. O espaço euclidiano tem três eixos de coordenadas mutuamente perpendiculares (x, y e z)), e três planos de coordenadas mutuamente perpendiculares (plano!coordinate}: o plano, plano e plano (Figura 1.1.2).

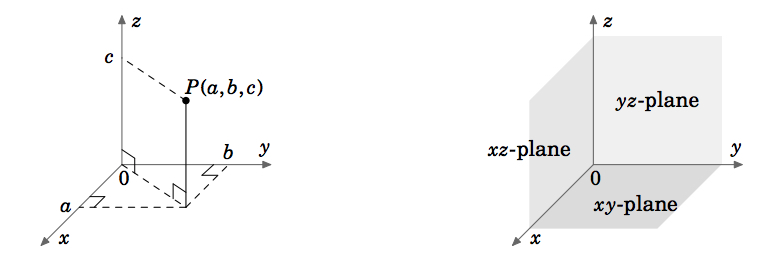
O sistema de coordenadas mostrado na Figura 1.1.1 é conhecido como um sistema de coordenadas \i1, porque é possível, usando a mão direita, apontar o dedo indicador no sentido positivo do eixo \i1, o dedo médio no sentido positivo do eixo \i1 e o polegar no sentido positivo do eixo \i1, como na Figura 1.1.3.

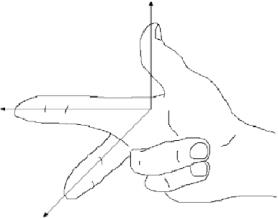
Fig 1.1.3: Sistema de coordenadas à direita.

Uma forma equivalente de definir um sistema à direita é se conseguir apontar o polegar para cima na direcção positiva {\i}-eixo enquanto usa os restantes quatro dedos para rodar o eixo {\i}-eixo em direcção ao eixo {\i}-eixo. Fazer a mesma coisa com a mão esquerda é o que define um sistema de coordenadas com a mão esquerda. Note que mudar os eixos num sistema com a mão direita resulta num sistema com a mão esquerda, e que rodar qualquer um dos tipos de sistema não altera a sua “mão esquerda”. Ao longo do livro utilizaremos um sistema destro.

Para funções de três variáveis, os gráficos existem no espaço 4-dimensional (i.e. \mathbb{R}^{4}}), que não podemos ver no nosso espaço 3-dimensional, quanto mais simular no espaço 2-dimensional. Portanto, só podemos pensar no espaço tetradimensional de forma abstrata. Para uma discussão divertida sobre este assunto, veja o livro da ABBOT.

Até agora, discutimos o \texto (posição) de um objeto no espaço bidimensional ou tridimensional. Mas e sobre algo como a velocidade do objeto, ou a sua aceleração? Ou a força gravitacional agindo sobre o objeto? Todos estes fenómenos parecem envolver movimento e (direcção de textura) de alguma forma. É aqui que entra a ideia de um {textit{vector}).

Você já lidou com velocidade e aceleração em cálculo de uma única variável. Por exemplo, para o movimento ao longo de uma linha reta, se \(y = f(t)}) dá o deslocamento de um objeto após o tempo, então \(dy/dt = f,'(t)}) é a velocidade do objeto no momento. A derivada é apenas um número, que é positivo se o objeto está se movendo em uma direção “positiva”, e negativo se ele se move na direção oposta àquela. Então você pode pensar naquele número, que foi chamado de velocidade do objeto, como tendo dois componentes: um número não negativo, indicado por um número não negativo, precedido por uma direção, indicado por um símbolo mais ou menos (representando o movimento na direção positiva ou na negativa, respectivamente), ou seja, um número qualquer (f(f,'(t) = pm a). Então, a magnitude da velocidade (normalmente chamada de “velocidade”) do objeto), e a velocidade representa a direção da velocidade (embora a direção positiva seja geralmente omitida).

Para o movimento em linha reta, ou seja, em um espaço unidimensional, as velocidades também estão contidas nesse espaço unidimensional, uma vez que são apenas números. Para o movimento geral ao longo de uma curva no espaço bidimensional ou tridimensional, no entanto, a velocidade terá de ser representada por um objecto multidimensional que deve ter tanto uma magnitude como uma direcção. Um objeto geométrico que tem essas características é uma seta, que em geometria elementar é chamada de “segmento de linha direcionada”. Esta é a motivação de como vamos definir um vector.

Para indicar a direcção de um vector, desenhamos uma seta do seu ponto inicial para o seu ponto terminal. Muitas vezes vamos denotar um vetor por uma única letra em negrito (por exemplo, \(\textbf{v})) e utilizaremos os termos “magnitude” e “comprimento” intercambiavelmente. Note que nossa definição poderia se aplicar a sistemas com qualquer número de dimensões (Figura 1.1.4 (a)-(c)).

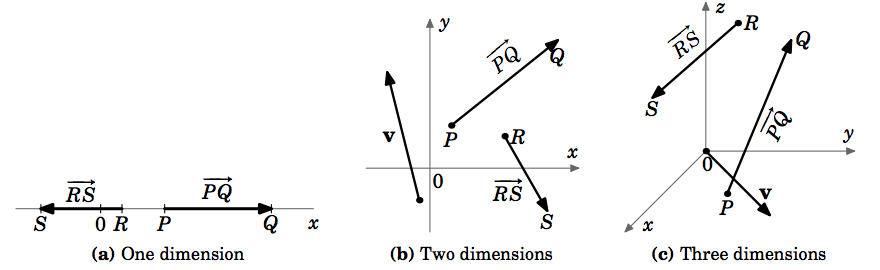
Algumas coisas precisam ser notadas sobre o vetor zero. Nossa motivação para o que um vetor inclui as noções de magnitude e direção. Qual é a magnitude do vetor zero? Nós o definimos como sendo zero, ou seja, {\i1}(\i1}norm{\i1}textbf{\i} = 0\i}. Isto concorda com a definição do vetor zero como apenas um ponto, que tem comprimento zero. E quanto à direção do vetor zero? Um único ponto não tem realmente uma direcção bem definida. Repare que tivemos o cuidado de definir apenas a direcção de um vector {textit{nonzero}, que é bem definido, uma vez que os pontos inicial e terminal são distintos. Nem todos concordam com a direção do vetor zero. Alguns afirmam que o vetor zero tem direção (ou seja, pode tomar qualquer direção), alguns dizem que tem direção (ou seja, a direção não pode ser determinada), enquanto outros dizem que tem direção (ou seja, não pode ser determinada). Nossa definição do vetor zero, entretanto, não requer que ele tenha uma direção, e vamos deixá-lo assim.

Agora que sabemos o que é um vetor, precisamos de uma maneira de determinar quando dois vetores são iguais. Isto nos leva à seguinte definição.

Por esta definição, vectores com a mesma magnitude e direcção mas com pontos iniciais diferentes seriam iguais. E vemos que o textobf e o textobf são paralelos, pois estão em linhas com a mesma inclinação, e apontam na mesma direcção. Portanto, apesar de terem pontos iniciais diferentes. Também vemos que o “textobf” é paralelo ao “textobf”, mas aponta na direcção oposta. Assim, vemos que há um número infinito de vectores para uma dada magnitude e direcção, sendo todos eles iguais e diferentes apenas pelos seus pontos iniciais e terminais. Existe um único vector que podemos escolher para representar todos esses vectores iguais? A resposta é sim, e é sugerida pelo vetor \(\textbf{w}) na Figura 1.1.5.

Pensar nos vectores como começando pela origem proporciona uma forma de lidar com os vectores de uma forma padrão, uma vez que cada sistema de coordenadas tem uma origem. Mas haverá momentos em que será conveniente considerar um ponto inicial diferente para um vector (por exemplo, ao adicionar vectores, o que faremos na secção seguinte). Outra vantagem de usar a origem como ponto inicial é que ela fornece uma correspondência fácil entre um vetor e seu ponto terminal.

Exemplo 1.1

Let \(\textbf{v}) be the vector in \(\mathbb{R}^{3}) whose initial point is at the origin and whose terminal point is \((3,4,5)\). Embora o ponto de texto e o vetor sejam objetos diferentes, é conveniente escrever “textobf” = (3,4,5)= (3,4,5)= (3,4,5)= (3,4,5)=). Ao fazer isso, entende-se que o ponto inicial do \\i(\i(\i(0,0,0,0)\i(3,4,5)\i(3,4,5)\i(952>

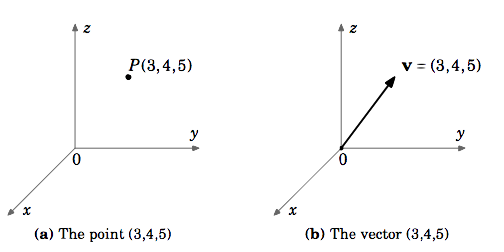
Sem indicação em contrário, quando nos referimos a vectores como \(\textbf{v} = (a,b)b)emmathbb{R}^^^ ou {2}(a,b,c){v} = (a,b,c)^) emmathbb{R^^^^3), queremos dizer vetores em coordenadas cartesianas começando na origem. Também, escreveremos o vetor zero em coordenadas cartesianas começando na origem. Além disso, escreveremos o vetor zero em coordenadas cartesianas começando na origem como {\i1}((0,0)0}) e {\i}(3) como {\i}((0,0)0)}((0,0,0)0)}, respectivamente.

A correspondência ponto-vetor fornece uma maneira fácil de verificar se dois vetores são iguais, sem ter que determinar sua magnitude e direção. Semelhante a ver se dois pontos são iguais, agora você está vendo se os pontos terminais dos vetores que começam na origem são os mesmos. Para cada vector, encontre o vector (único!) que é igual a cujo ponto inicial é a origem. Depois compare as coordenadas dos pontos terminais desses vetores “novos”: se essas coordenadas forem as mesmas, então os vetores originais são iguais. Para obter os vetores “novos” começando na origem, você \(\textit{traduzir) cada vetor para começar na origem, subtraindo as coordenadas do ponto inicial original do ponto terminal original. O ponto resultante será o ponto terminal do vetor “novo” cujo ponto inicial é a origem. Faça isto para cada vector original e depois compare.

Exemplo 1.2

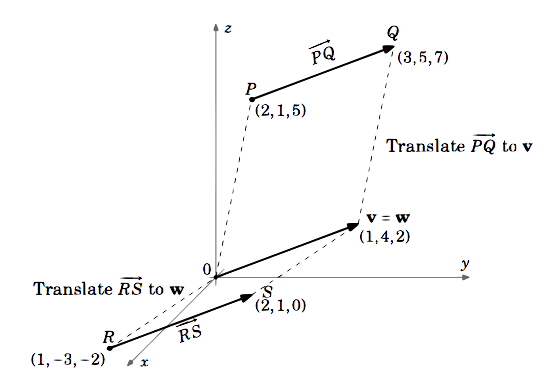
Considerar os vetores \(PQ) e \(PQ) em \(R), onde \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)}) e \(S = (2,1,0)}). Será que o “Overrightarrow” (PQ) = “Overrightarrow” (S = (2,1,0))?

O vector {\PQ} é igual ao vector {\PQ} com o ponto inicial ((0,0,0,0)}) e o ponto terminal {\P – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)}.
Similiarmente, {RS}} é igual ao vetor \\(\textbf{w}) com ponto inicial \((0,0,0,0)\) e ponto terminal \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1,1,1 – (-3),0 – (-2)) = (1,4,2)\).
Então {PQ} = {v} = (1,4,2)} e {RS} = {w} = (1,4,2)}.
{\i1}(antes antes de sobrelinha direita{\i} = sobrelinha direita{\i}

Recall a fórmula da distância para pontos no plano euclidiano:

Por esta fórmula, temos o seguinte resultado:

Decifrar a magnitude de um vector {v} = (a,b)} em {R}^{2}) é um caso especial da fórmula acima com \(P = (0,0)}) e \(Q = (a,b)}):

Para calcular a magnitude dos vectores em \\(\mathbb{R}^{3}}, precisamos de uma fórmula de distância para pontos no espaço euclidiano (adiaremos a prova para a próxima secção):

A prova vai usar o seguinte resultado:

Prova: Há quatro casos a considerar:
(\textit{Case 1:}) \(a = b = c = 0\). Então \(\textbf{v} = \textbf{0}), então \(\textbf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2}} = ^sqrt{a^{2} + b^{2} + c^{2}.

(2:2:2)(a, b, c) são Sem perda de generalidade, assumimos que as duas outras possibilidades (a = b = 0) e (c = 0) (as outras duas possibilidades são tratadas de forma semelhante). Então, o textobf{v} = (0,0,c)}, que é um vector de comprimento ao longo do eixo. Então, {\i1}{\i1}- Então, {\i1}norm{\i} = | c | = |sqrt{c^{\i} = |sqrt{0^{\i} + 0^{2} + c^{2}} = ^sqrt{a^{2} + b^{2} + c^{2}.
(xxxxxxtit{\a3:{\a3:})(xxxxxxtit{\a3:{\a3:{\a3:{\a3:}).(2).(2). Sem perda de generalidade, podemos assumir que a, b, c são todas positivas (as outras sete possibilidades são tratadas de forma semelhante). Considere os pontos \(P = (0,0,0)0), \(Q = (a,b,c)\), \(R =(a,b,0),\) e \(S = (a,0,0)0)\), como mostrado na Figura 1.1.8. Aplicando o Teorema de Pitágoras ao triângulo direito (triângulo PSR), obtém-se o PR da esquerda para a direita (2) = a^{2} + b^{2}). Uma segunda aplicação do Teorema de Pitágoras, desta vez para o triângulo direito PQR, dá o seguinte: PQ PQ direita = PQ esquerda = PQ direita = PQ esquerda = PQ direita = PQ esquerda = PQ direita = PQ esquerda = PQ esquerda = PQ direita = PQ esquerda = PQ direita +esquerda QR Direita QR Direita QR Direita QR + b^{2} + c^{2}}\). Isto prova o teorema.

({\i1}({\i1}({\i1}textobf{QED})}