11.1: Sisteme de coordonate tridimensionale
În calculul cu o singură variabilă, funcțiile pe care le întâlnim sunt funcții ale unei variabile (de obicei \(x\) sau \(t\)) care variază pe un subansamblu al dreptei numerelor reale (pe care o notăm cu \(\mathbb{R}\)). Pentru o astfel de funcție, de exemplu, \(y = f(x)\), \(\textbf{graph}\) a funcției \(f\) constă din punctele \((x, y) = (x, f(x))\). Aceste puncte se află în \(\textbf{planul euclidian}\), care, în sistemul de coordonate \(\textbf{cartezian}\) sau \(\textbf{rectangular}\), este format din toate perechile ordonate de numere reale \((a, b)\). Folosim cuvântul „euclidian” pentru a desemna un sistem în care se aplică toate regulile obișnuite ale geometriei euclidiene. Planul euclidian este notat cu \(\mathbb{R}^{2}\); „2” reprezintă numărul de \(\texte{dimensiuni}\) ale planului. Planul euclidian are două \(\textbf{axe de coordonate}\) perpendiculare: axa \(x\) și axa \(y\).
În calculul vectorial (sau multivariabil), vom avea de-a face cu funcții de două sau trei variabile (de obicei \(x, y\) sau \(x, y, z\), respectiv \(x, y, z\)). Graficul unei funcții de două variabile, de exemplu, \(z = f(x,y)\), se află în spațiul euclidian, care, în sistemul de coordonate carteziene, este format din toate triplele ordonate de numere reale \((a, b, c)\). Deoarece spațiul euclidian este tridimensional, îl desemnăm prin \(\mathbb{R}^{3}\). Graficul lui \(f\) este format din punctele \((x, y, z) = (x, y, f(x, y))\). Sistemul de coordonate tridimensionale al spațiului euclidian poate fi reprezentat pe o suprafață plană, cum ar fi această pagină sau o tablă, doar dând iluzia celor trei dimensiuni, în modul prezentat în figura 1.1.1. Spațiul euclidian are trei axe de coordonate perpendiculare între ele (\(x, y\) și \(z\)) și trei planuri de coordonate perpendiculare între ele\index{plan!coordonate}: planul \(xy\)-planul, planul \(yz\)-planul și planul \(xz\)-planul (Figura 1.1.2).
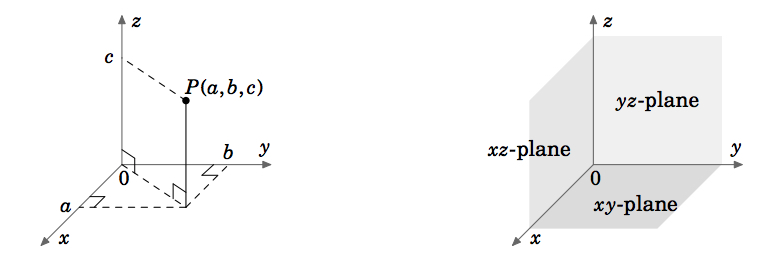
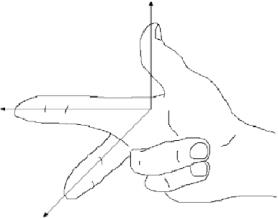
Sistemul de coordonate prezentat în Figura 1.1.1 este cunoscut sub numele de \(\textbf{sistem de coordonate pentru dreptaci}\), deoarece este posibil, folosind mâna dreaptă, să se îndrepte degetul arătător în direcția pozitivă a axei \(x\), degetul mijlociu în direcția pozitivă a axei \(y\), iar degetul mare în direcția pozitivă a axei \(z\), ca în figura 1.1.1.3.
Figură 1.1.3: Sistem de coordonate drepte.
O modalitate echivalentă de a defini un sistem de coordonate drepte este dacă puteți îndrepta degetul mare în sus, în direcția pozitivă a axei \(z\), în timp ce folosiți celelalte patru degete pentru a roti axa \(x\) spre axa \(y\). Același lucru cu mâna stângă este ceea ce definește un \(\textbf{sistem de coordonate cu mâna stângă}\). Observați că schimbarea axelor \(x\) și \(y\) într-un sistem de coordonate pentru dreptaci are ca rezultat un sistem pentru stângaci și că rotirea oricăruia dintre cele două tipuri de sisteme nu-i schimbă „mâna”. De-a lungul cărții vom folosi un sistem dreptaci.
Pentru funcțiile de trei variabile, graficele există în spațiul cvadridimensional (adică \(\mathbb{R}^{4}\)), pe care nu îl putem vedea în spațiul nostru tridimensional, cu atât mai puțin simula în spațiul bidimensional. Prin urmare, nu ne putem gândi la spațiul 4-dimensional decât în mod abstract. Pentru o discuție amuzantă pe această temă, consultați cartea lui ABBOT.
Până acum am discutat despre \(\textul{poziția}\) unui obiect în spațiul bidimensional sau tridimensional. Dar cum rămâne cu ceva precum viteza obiectului sau accelerația acestuia? Sau forța gravitațională care acționează asupra obiectului? Toate aceste fenomene par să implice într-un fel sau altul mișcarea și \(\textit{direcția}\). Aici intervine ideea de \(\textit{vector}\).
Ai abordat deja viteza și accelerația în calculul cu o singură variabilă. De exemplu, pentru mișcarea de-a lungul unei linii drepte, dacă \(y = f(t)\) dă deplasarea unui obiect după un timp \(t\), atunci \(dy/dt = f\,'(t)\) este viteza obiectului la momentul \(t\). Derivata \(f\(f\,'(t)\)) este doar un număr, care este pozitiv dacă obiectul se deplasează într-o direcție „pozitivă” convenită și negativ dacă se deplasează în direcția opusă acelei direcții. Așadar, vă puteți gândi la acel număr, care a fost numit viteza obiectului, ca având două componente: un \(\(\textit{magnitudine}\), indicat de un număr nenegativ, precedat de o direcție, indicată de un simbol plus sau minus (reprezentând mișcarea în direcția pozitivă, respectiv negativă), adică \(f\,'(t) = \pm a\) pentru un număr \(a \ge 0\). Atunci \(a\) este magnitudinea vitezei (numită în mod normal \(\textul{viteza}\) obiectului), iar \(\pm\) reprezintă direcția vitezei (deși \(+\) este de obicei omis pentru direcția pozitivă).
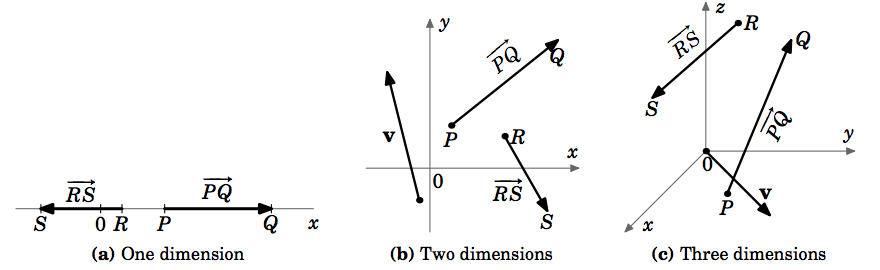
Pentru mișcarea de-a lungul unei linii drepte, adică într-un spațiu unidimensional, vitezele sunt, de asemenea, conținute în acel spațiu unidimensional, deoarece ele sunt doar numere. Cu toate acestea, pentru mișcarea generală de-a lungul unei curbe într-un spațiu bidimensional sau tridimensional, viteza va trebui să fie reprezentată de un obiect multidimensional care ar trebui să aibă atât o mărime, cât și o direcție. Un obiect geometric care are aceste caracteristici este o săgeată, care în geometria elementară se numește „segment de dreaptă dirijat”. Aceasta este motivația pentru modul în care vom defini un vector.
Definiție 1.1
Un \(\textbf{vector}\) (nenul) este un segment de dreaptă dirijat trasat de la un punct \(P\) (numit \(\textbf{punctul inițial}\)) până la un punct \(Q\) (numit \(\textbf{punctul terminal}\)), \(P\) și \(Q\) fiind puncte distincte. Vectorul este notat cu \(\(\spredreaptafată{PQ}\). Lungimea lui \(\textbf{magnitudine}\) este lungimea segmentului de dreaptă, notat cu \(\norm{\supra-dreapta-sfârșită{PQ}}\), iar \(\textbf{direcție}\) este aceeași cu cea a segmentului de dreaptă dirijat. \(\(\textbf{vectori zero}\) este doar un punct și este notat cu \(\textbf{0}\).
Pentru a indica direcția unui vector, tragem o săgeată din punctul său inițial până în punctul său terminal. Deseori vom desemna un vector printr-o singură literă cu litere îngroșate (de exemplu, \(\textbf{v}\)) și vom folosi interschimbabil termenii „magnitudine” și „lungime”. Rețineți că definiția noastră se poate aplica la sisteme cu orice număr de dimensiuni (figura 1.1.4 (a)-(c)).
Trebuie notate câteva lucruri despre vectorul zero. Motivația noastră pentru ceea ce este un vector a inclus noțiunile de mărime și direcție. Care este magnitudinea vectorului zero? Îl definim ca fiind zero, adică \(\norm{\textbf{0}} = 0\). Acest lucru este în concordanță cu definiția vectorului zero ca fiind doar un punct, care are lungimea zero. Cum rămâne cu direcția vectorului zero? Un singur punct nu are într-adevăr o direcție bine definită. Observați că am avut grijă să definim doar direcția unui vector \(\textit{non-zero}\), care este bine definit, deoarece punctele inițiale și terminale sunt distincte. Nu toată lumea este de acord cu direcția vectorului zero. Unii susțin că vectorul zero are o direcție \(\textit{arbitrar}\) (adică poate lua orice direcție), alții spun că are o direcție \(\textit{indeterminată}\) (adică direcția nu poate fi determinată), în timp ce alții spun că are o direcție \(\textit{nu}\). Cu toate acestea, definiția noastră a vectorului zero nu cere ca acesta să aibă o direcție și o vom lăsa așa.
Acum că știm ce este un vector, avem nevoie de o modalitate de a determina când doi vectori sunt egali. Acest lucru ne conduce la următoarea definiție.
Definiția 1.2
Doi vectori nenule sunt \(\textbf{egal}\) dacă au aceeași mărime și aceeași direcție. Orice vector cu magnitudine zero este egal cu vectorul zero.
Potrivit acestei definiții, vectorii cu aceeași magnitudine și direcție, dar cu puncte inițiale diferite, ar fi egali. De exemplu, în figura 1.1.5 vectorii \(\textbf{u}\), \(\textbf{v}\) și \(\textbf{w}\) au toți aceeași mărime \(\sqrt{5}\) (prin Teorema lui Pitagora). Vedem că \(\textbf{u}\) și \(\textbf{w}\) sunt paralele, deoarece se află pe drepte care au aceeași pantă \(\frac{1}{2}\) și sunt orientate în aceeași direcție. Deci \(\textbf{u} = \textbf{w}\), chiar dacă au puncte inițiale diferite. Vedem, de asemenea, că \(\textbf{v}\) este paralelă cu \(\textbf{u}\), dar arată în direcția opusă. Deci \(\textbf{u} \ne \textbf{v}\).
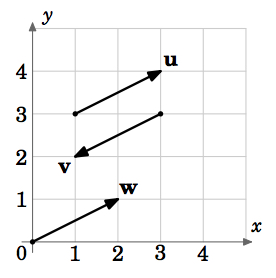
Pe cale de consecință, putem vedea că există un număr infinit de vectori pentru o mărime și o direcție date, acești vectori fiind toți egali și diferind doar prin punctele lor inițiale și terminale. Există un singur vector pe care îl putem alege pentru a reprezenta toți acești vectori egali? Răspunsul este da și este sugerat de vectorul \(\textbf{w}\) din figura 1.1.5.
Dacă nu se indică altfel, atunci când vorbim de „vectorul” cu o mărime și o direcție date, ne vom referi la cel al cărui punct inițial se află la originea sistemului de coordonate.
Gândirea vectorilor ca pornind de la origine oferă o modalitate de a trata vectorii într-un mod standard, deoarece fiecare sistem de coordonate are o origine. Dar vor exista momente în care va fi convenabil să se ia în considerare un punct inițial diferit pentru un vector (de exemplu, atunci când adunăm vectori, ceea ce vom face în secțiunea următoare). Un alt avantaj al utilizării originii ca punct inițial este acela că oferă o corespondență ușoară între un vector și punctul său terminal.
Exemplu 1.1
Fie \(\textbf{v}\) vectorul din \(\mathbb{R}^{3}\) al cărui punct inițial este la origine și al cărui punct terminal este \((3,4,5)\). Deși \(\(\textit{punct}\) \((3,4,5)\) și vectorul \(\textbf{v}\) sunt obiecte diferite, este convenabil să se scrie \(\textbf{v} = (3,4,5)\). Când se face acest lucru, se înțelege că punctul inițial al lui \(\textbf{v}\) este la originea \((0,0,0)\) și punctul terminal este \((3,4,5)\).
Dacă nu se specifică altfel, când ne referim la vectori ca \(\textbf{v} = (a,b)\) în \(\mathbb{R}^{2}\) sau \(\textbf{v} = (a,b,c)\) în \(\mathbb{R}^{3}\), ne referim la vectori în coordonate carteziene care pornesc de la origine. De asemenea, vom scrie vectorul zero \(\textbf{0}\) în \(\mathbb{R}^{2}\) și \(\mathbb{R}^{3}\) ca \((0,0)\) și, respectiv, \((0,0,0)\).
Corespondența punct-vector oferă o modalitate ușoară de a verifica dacă doi vectori sunt egali, fără a fi nevoie să le determinăm mărimea și direcția. Similar cu a vedea dacă două puncte sunt identice, acum vedeți dacă punctele terminale ale vectorilor care pornesc de la origine sunt identice. Pentru fiecare vector, găsiți vectorul (unic!) pe care îl egalează și al cărui punct inițial este originea. Apoi comparați coordonatele punctelor terminale ale acestor „noi” vectori: dacă aceste coordonate sunt aceleași, atunci vectorii inițiali sunt egali. Pentru a obține vectorii „noi” care pornesc de la origine, trebuie să \(\textit{translate}\) fiecare vector să pornească de la origine prin scăderea coordonatelor punctului inițial original din punctul terminal original. Punctul rezultat va fi punctul terminal al „noului” vector al cărui punct inițial este originea. Faceți acest lucru pentru fiecare vector original, apoi comparați.
Exemplu 1.2
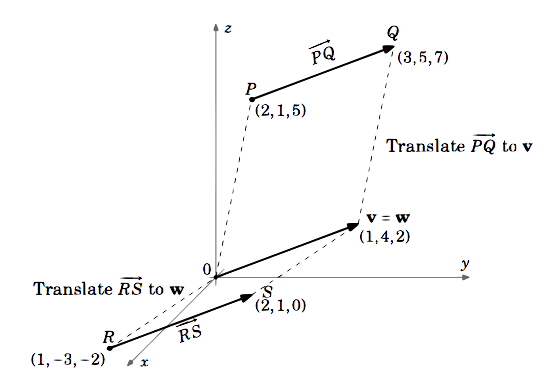
Considerați vectorii \(\(\spre dreapta-sfârșită{PQ}\) și \(\spre dreapta-sfârșită{RS}\) în \(\mathbb{R}^{3}\), unde \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\) și \(S = (2,1,0)\). Are \(\overrightarrow{PQ} = \overrightarrow{RS}\)?
Vectorialul \(\overrightarrow{PQ}\) este egal cu vectorul \(\textbf{v}\) cu punctul inițial \((0,0,0)\) și punctul terminal \(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\).
În mod similar, \(\overrightarrow{RS}\) este egal cu vectorul \(\textbf{w}\) cu punctul inițial \((0,0,0)\) și punctul terminal \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1, 1 – (-3),0 – (-2)) = (1,4,2)\).
Deci \(\(\overrightarrow{PQ} = \textbf{v} = (1,4,2)\) și \(\overrightarrow{RS} = \textbf{w} = (1,4,2)\).
\(\ așadar \overrightarrow{PQ} = \overrightarrow{RS}\)
Reamintim formula distanței pentru punctele din planul euclidian:
Pentru punctele \(P = (x_{1}, y_{1})\), \(Q = (x_{2}, y_{2})\) din \(\mathbb{R}^{2}\), distanța \(d\) dintre \(P\) și \(Q\) este:
\
Potrivit acestei formule, avem următorul rezultat:
Nota
Pentru un vector \(\spre-dreapta-sfârșită{PQ}\) în \(\mathbb{R}^{2}\) cu punctul inițial \(P = (x_{1}, y_{1})\) și un punct terminal \(Q = (x_{2}, y_{2})\), mărimea lui \(\(\supra-dreapta-sfârșită{PQ}\) este:
\
Căutarea mărimii unui vector \(\textbf{v} = (a,b)\) în \(\mathbb{R}^{2}\) este un caz special al formulei de mai sus cu \(P = (0,0)\) și \(Q = (a,b)\):
Pentru un vector \(\textbf{v} = (a,b)\) în \(\mathbb{R}^{2}\), mărimea lui \(\textbf{v}\) este:
\
Pentru a calcula mărimea vectorilor în \(\mathbb{R}^{3}\), avem nevoie de o formulă de distanță pentru punctele din spațiul euclidian (vom amâna demonstrația până în secțiunea următoare):
Teorema 1.1
Distanța \(d\) dintre punctele \(P = (x_{1}, y_{1}, z_{1})\) și \(Q = (x_{2}, y_{2}, z_{2}, z_{2})\ în \(\mathbb{R}^{3}\) este:
\
Demonstrarea va folosi următorul rezultat:
Teorema 1.2
Pentru un vector \(\textbf{v} = (a,b,c)\) în \(\mathbb{R}^{3}\), mărimea lui \(\textbf{v}\) este:
\
Demonstrație: Există patru cazuri de luat în considerare:
\(\textit{Cazul 1:}\) \(a = b = c = 0\). Atunci \(\textbf{v} = \textbf{0}\), deci \(\norm{\textbf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2}} = \sqrt{a^{2} + b^{2} + c^{{2}}}\).
\(\textit{Cazul 2:}\) \(\textit{exact două din }\)\(a, b, c\) sunt \(0\). Fără pierdere de generalitate, presupunem că \(a = b = 0\) și \(c \ne 0\) (celelalte două posibilități sunt tratate în mod similar). Atunci \(\textbf{v} = (0,0,c)\), care este un vector de lungime \(|c|\) de-a lungul axei \(z\). Deci \(\norm{\textbf{v}} = | c | = \sqrt{c^{2}} = \sqrt{0^{2} + 0^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{{2}}}\).
\(\textit{Cazul 3:}\) \(\textit{exact unul dintre }\)\(a, b, c\) este \(0\). Fără a pierde din generalitate, presupunem că \(a = 0\), \(b \ne 0\) și \(c \ne 0\) (celelalte două posibilități sunt tratate în mod similar). Atunci \(\(\textbf{v} = (0,b,c)\), care este un vector în planul \(yz\), deci prin Teorema lui Pitagora avem \(\norm{\textbf{v}} = \sqrt{b^{2} + c^{{2}} = \sqrt{0^{2} + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{{2}}}\).
\(\textit{Cazul 4:}\) \(\textit{nimic din }\)\(a, b, c\) sunt \(0\). Fără pierdere de generalitate, putem presupune că \(a, b, c\) sunt toate pozitive (celelalte șapte posibilități sunt tratate în mod similar). Considerați punctele \(P = (0,0,0)\), \(Q = (a,b,c)\), \(R =(a,b,0),\) și \(S = (a,0,0)\), așa cum se arată în figura 1.1.8. Aplicând teorema lui Pitagora la triunghiul dreptunghic \(\triunghiul PSR\) se obține \(\stânga\vert PR \ dreapta\vert^{2} = a^{2} + b^{2}\). O a doua aplicare a Teoremei lui Pitagora, de data aceasta la triunghiul dreptunghic \(\triunghi PQR\), dă \(\norm{\textbf{v}} = \left\lvert PQ \right\rvert = \sqrt{\left\vert PR \right\vert^{2} + \left\vert QR \right\vert^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}\). Acest lucru dovedește teorema.
\(\tag{\(\textbf{QED}\)}\)
Exemplu 1.3
Calculați următoarele:
- Mărimea vectorului \(\(\overrightarrow{PQ}\) în \(\mathbb{R}^{2}\) cu \(P = (-1,2)\) și \(Q = (5,5)\).
\( \textit{Soluție:}\) Prin formula (1.2), \(\norm{\overrightarrow{PQ}} = \sqrt{(5 – (-1))^{2} + (5 – 2)^{2}}} = \sqrt{36 + 9} = \sqrt{45} = 3 \sqrt{5}\). - Mărimea vectorului \(\textbf{v} = (8,3)\) în \(\mathbb{R}^{2}\).
\(\textit{Soluție:}\) Prin formula (1.3), \(\norm{\textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}\). - Distanța dintre punctele \(P = (2, -1, 4)\) și \(Q = (4, 2, -3)\) în \(\mathbb{R}^{2}\).
\(\textit{Solution:}\) Prin formula (1.4), distanța \(d = \sqrt{(4 – 2)^{2} + (2 – (-1))^{2} + (-3 – 4)^{2}}} = \sqrt{4 + 9 + 49} = \sqrt{62}\). - Mărimea vectorului \(\textbf{v} = (5,8,-2)\) în \(\mathbb{R}^{3}\).
\(\textit{Soluție:}\) Prin formula (1.5), \(\norm{\textbf{v}} = \sqrt{5^{2} + 8^{2} + (-2)^{2}}} = \sqrt{25 + 64 + 4} = \sqrt{93}\).
Contribuții și atribuții
-
Michael Corral (Schoolcraft College). Conținutul acestei pagini este distribuit în conformitate cu termenii licenței GNU Free Documentation License, versiunea 1.2.
.