11.1 : Systèmes de coordonnées tridimensionnels
Dans le calcul à une variable, les fonctions que l’on rencontre sont des fonctions d’une variable (généralement \(x\) ou \(t\)) qui varie sur un certain sous-ensemble de la ligne des nombres réels (que nous désignons par \(\mathbb{R}\)). Pour une telle fonction, par exemple \(y = f(x)\), le \(\textbf{graph}\) de la fonction \(f\) est constitué des points \((x, y) = (x, f(x))\). Ces points se trouvent dans le « plan euclidien » qui, dans le système de coordonnées « cartésien » ou « rectangulaire », est constitué de toutes les paires ordonnées de nombres réels « (a, b)\ ». Nous utilisons le mot « euclidien » pour désigner un système dans lequel toutes les règles habituelles de la géométrie euclidienne s’appliquent. Nous désignons le plan euclidien par \(\mathbb{R}^{2}\) ; le « 2 » représente le nombre de \(\textit{dimensions}\) du plan. Le plan euclidien possède deux \(\textbf{axes de coordonnées}\) perpendiculaires : l’axe \(x\) et l’axe \(y\).
En calcul vectoriel (ou multivariable), nous traiterons des fonctions de deux ou trois variables (habituellement \(x, y\) ou \(x, y, z\), respectivement). Le graphe d’une fonction à deux variables, par exemple \(z = f(x,y)\), se situe dans l’espace euclidien qui, dans le système de coordonnées cartésiennes, est constitué de tous les triplets ordonnés de nombres réels \((a, b, c)\). L’espace euclidien étant tridimensionnel, nous le désignons par \(\mathbb{R}^{3}\). Le graphe de \(f\) est constitué des points \((x, y, z) = (x, y, f(x, y))\). Le système de coordonnées tridimensionnel de l’espace euclidien ne peut être représenté sur une surface plane, telle que cette page ou un tableau noir, qu’en donnant l’illusion de trois dimensions, comme le montre la figure 1.1.1. L’espace euclidien possède trois axes de coordonnées mutuellement perpendiculaires (\(x, y\) et \(z\)), et trois plans de coordonnées mutuellement perpendiculaires \index{plane !coordinate} : le plan \(xy\)-, le plan \(yz\)- et le plan \(xz\)- (figure 1.1.2).
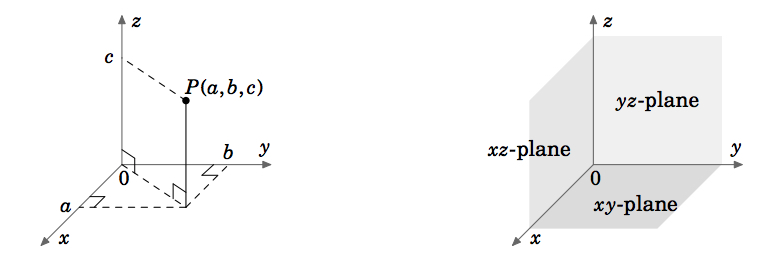
Le système de coordonnées représenté sur la figure 1.1.1 est connu sous le nom de \(\textbf{système de coordonnées pour droitiers}\), car il est possible, en utilisant la main droite, de pointer l’index dans la direction positive de l’axe \(x\), le majeur dans la direction positive de l’axe \(y\), et le pouce dans la direction positive de l’axe \(z\), comme dans la figure 1.1.3.
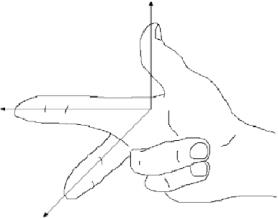
Fig 1.1.3 : Système de coordonnées droitier.
Une manière équivalente de définir un système droitier est si vous pouvez pointer votre pouce vers le haut dans la direction positive de l’axe \(z\) tout en utilisant les quatre autres doigts pour faire tourner l’axe \(x\) vers l’axe \(y\). Faire la même chose avec la main gauche est ce qui définit un \(\textbf{système de coordonnées de la main gauche}\). Remarquez que l’inversion des axes \(x\) et \(y\) dans un système droitier donne un système gaucher, et que la rotation de l’un ou l’autre type de système ne change pas sa « maniabilité ». Dans tout le livre, nous utiliserons un système droitier.
Pour les fonctions de trois variables, les graphes existent dans un espace à 4 dimensions (c’est-à-dire \(\mathbb{R}^{4}\)), que nous ne pouvons pas voir dans notre espace à 3 dimensions, et encore moins simuler dans un espace à 2 dimensions. Nous ne pouvons donc penser à l’espace quadridimensionnel que de manière abstraite. Pour une discussion divertissante sur ce sujet, voir le livre de ABBOT.
Jusqu’à présent, nous avons discuté de la \(\textit{position}\) d’un objet dans un espace à 2 ou 3 dimensions. Mais qu’en est-il de quelque chose comme la vitesse de l’objet, ou son accélération ? Ou de la force gravitationnelle agissant sur l’objet ? Ces phénomènes semblent tous impliquer le mouvement et la direction d’une manière ou d’une autre. C’est là qu’intervient l’idée d’un \(\textit{vecteur}\).
Vous avez déjà traité de la vitesse et de l’accélération dans le calcul à une variable. Par exemple, pour un mouvement le long d’une ligne droite, si \(y = f(t)\) donne le déplacement d’un objet après le temps \(t\), alors \(dy/dt = f\,'(t)\) est la vitesse de l’objet au temps \(t\). La dérivée \(f\,'(t)\) est juste un nombre, qui est positif si l’objet se déplace dans une direction « positive » convenue, et négatif s’il se déplace dans la direction opposée à cette direction. On peut donc considérer que ce nombre, appelé vitesse de l’objet, a deux composantes : un \(\textit{magnitude}\), indiqué par un nombre non négatif, précédé d’une direction, indiquée par un symbole plus ou moins (représentant le mouvement dans la direction positive ou la direction négative, respectivement), c’est-à-dire \(f\,'(t) = \pm a\) pour un certain nombre \(a \ge 0\). Alors \(a\) est la magnitude de la vitesse (normalement appelée \(\textit{speed}\) de l’objet), et le \(\pm\) représente la direction de la vitesse (bien que le \(+\) soit habituellement omis pour la direction positive).
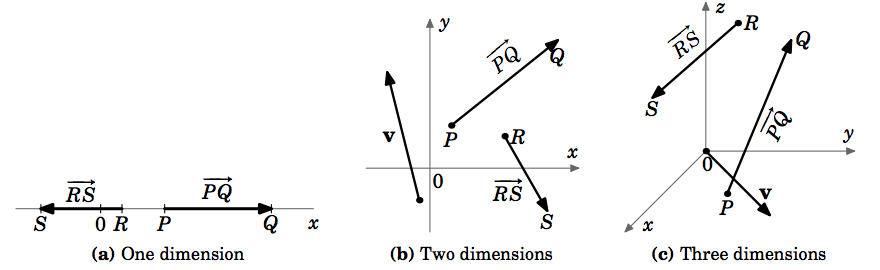
Pour le mouvement le long d’une ligne droite, c’est-à-dire dans un espace à 1 dimension, les vitesses sont également contenues dans cet espace à 1 dimension, puisqu’elles sont juste des nombres. Cependant, pour un mouvement général le long d’une courbe dans un espace à 2 ou 3 dimensions, la vitesse devra être représentée par un objet multidimensionnel qui devra avoir à la fois une magnitude et une direction. Un objet géométrique qui possède ces caractéristiques est une flèche, que l’on appelle en géométrie élémentaire un « segment de droite dirigé ». C’est ce qui motive la façon dont nous allons définir un vecteur.
Définition 1.1
Un vecteur (non nul) \(\textbf{vector}\) est un segment de droite dirigé tracé d’un point \(P\) (appelé son \(\textbf{point initial}\)) à un point \(Q\) (appelé son \(\textbf{point terminal}\)), avec \(P\) et \(Q\) étant des points distincts. Le vecteur est désigné par \(\overrightarrow{PQ}\). Son \(\textbf{magnitude}\) est la longueur du segment de droite, désigné par \(\norm{\overrightarrow{PQ}}\), et son \(\textbf{direction}\) est le même que celui du segment de droite dirigé. Le \(\textbf{vecteur nul}\) est juste un point, et il est dénoté par \(\textbf{0}\).
Pour indiquer la direction d’un vecteur, on dessine une flèche de son point initial à son point terminal. Nous désignerons souvent un vecteur par une seule lettre en gras (par exemple : \(\textbf{v}\)) et nous utiliserons indifféremment les termes « magnitude » et « longueur ». Notez que notre définition pourrait s’appliquer à des systèmes ayant un nombre quelconque de dimensions (figure 1.1.4 (a)-(c)).
Il faut noter quelques choses à propos du vecteur zéro. Notre motivation pour ce qu’est un vecteur incluait les notions de magnitude et de direction. Quelle est la magnitude du vecteur zéro ? Nous le définissons comme étant nul, c’est-à-dire \(\norm{\textbf{0}} = 0\). Ceci est en accord avec la définition du vecteur zéro comme un simple point, dont la longueur est nulle. Qu’en est-il de la direction du vecteur zéro ? Un point unique n’a pas vraiment de direction bien définie. Remarquez que nous avons pris soin de ne définir que la direction d’un vecteur \(\textit{nonzero}\), qui est bien défini puisque les points initial et terminal sont distincts. Tout le monde n’est pas d’accord sur la direction du vecteur zéro. Certains prétendent que le vecteur zéro a une direction \(\textit{arbitrary}\) (c’est-à-dire qu’il peut prendre n’importe quelle direction), d’autres disent qu’il a une direction \(\textit{indeterminate}\) (c’est-à-dire que la direction ne peut pas être déterminée), tandis que d’autres encore disent qu’il a une direction \(\textit{no}\). Notre définition du vecteur zéro, cependant, n’exige pas qu’il ait une direction, et nous allons en rester là.
Maintenant que nous savons ce qu’est un vecteur, nous avons besoin d’un moyen de déterminer quand deux vecteurs sont égaux. Cela nous conduit à la définition suivante.
Définition 1.2
Deux vecteurs non nuls sont \(\textbf{equal}\) s’ils ont la même magnitude et la même direction. Tout vecteur de magnitude nulle est égal au vecteur nul.
Selon cette définition, des vecteurs de même magnitude et de même direction mais dont les points initiaux sont différents seraient égaux. Par exemple, sur la figure 1.1.5, les vecteurs \(\textbf{u}\), \(\textbf{v}\) et \(\textbf{w}\) ont tous la même magnitude \(\sqrt{5}\) (par le théorème de Pythagore). Et nous voyons que \(\textbf{u}\) et \(\textbf{w}\) sont parallèles, puisqu’ils se trouvent sur des lignes ayant la même pente \(\frac{1}{2}\), et qu’ils pointent dans la même direction. Donc \(\textbf{u} = \textbf{w}\), même si leurs points initiaux sont différents. Nous voyons également que \(\textbf{v}\) est parallèle à \(\textbf{u}\) mais pointe dans la direction opposée. Donc \(\textbf{u} \ne \textbf{v}\).
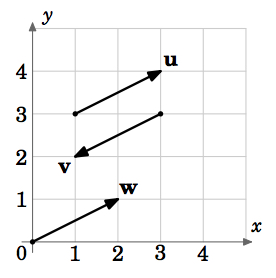
On voit donc qu’il existe une infinité de vecteurs pour une grandeur et une direction données, ces vecteurs étant tous égaux et ne différant que par leurs points initiaux et terminaux. Existe-t-il un vecteur unique que nous pouvons choisir pour représenter tous ces vecteurs égaux ? La réponse est oui, et elle est suggérée par le vecteur \(\textbf{w}\) de la figure 1.1.5.
Sauf indication contraire, en parlant du « vecteur » de magnitude et de direction données, nous désignerons celui dont le point initial est à l’origine du système de coordonnées.
Penser que les vecteurs partent de l’origine permet de traiter les vecteurs de manière standard, puisque chaque système de coordonnées a une origine. Mais il y aura des moments où il sera pratique de considérer un point initial différent pour un vecteur (par exemple, lors de l’addition de vecteurs, ce que nous ferons dans la section suivante). Un autre avantage d’utiliser l’origine comme point initial est qu’il fournit une correspondance facile entre un vecteur et son point terminal.
Exemple 1.1
Soit \(\textbf{v}\) le vecteur dans \(\mathbb{R}^{3}\) dont le point initial est à l’origine et dont le point terminal est \((3,4,5)\). Bien que le \(\textit{point}\) \((3,4,5)\) et le vecteur \(\textbf{v}\) soient des objets différents, il est pratique d’écrire \(\textbf{v} = (3,4,5)\). En faisant cela, on comprend que le point initial de \(\textbf{v}\) est à l’origine \((0,0,0)\) et le point terminal est \((3,4,5)\).
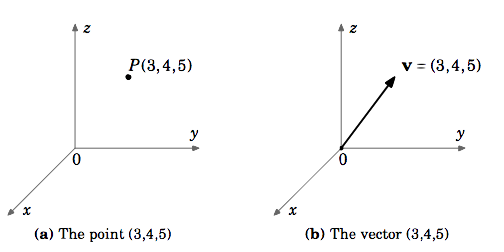
Sauf indication contraire, lorsque nous nous référons aux vecteurs comme \(\textbf{v} = (a,b)\) dans \(\mathbb{R}^{2}\) ou \(\textbf{v} = (a,b,c)\) dans \(\mathbb{R}^{3}\), nous désignons des vecteurs en coordonnées cartésiennes commençant à l’origine. De même, nous écrirons le vecteur zéro \(\textbf{0}\) dans \(\mathbb{R}^{2}\) et \(\mathbb{R}^{3}\) comme \((0,0)\) et \((0,0,0)\), respectivement.
La correspondance point-vecteur fournit un moyen facile de vérifier si deux vecteurs sont égaux, sans avoir à déterminer leur magnitude et leur direction. Semblable à voir si deux points sont les mêmes, vous voyez maintenant si les points terminaux des vecteurs commençant à l’origine sont les mêmes. Pour chaque vecteur, trouvez le vecteur (unique !) qu’il égale et dont le point initial est l’origine. Comparez ensuite les coordonnées des points terminaux de ces « nouveaux » vecteurs : si ces coordonnées sont les mêmes, alors les vecteurs originaux sont égaux. Pour obtenir les « nouveaux » vecteurs commençant à l’origine, vous \(\N-textit{translate}\) chaque vecteur pour commencer à l’origine en soustrayant les coordonnées du point initial original du point terminal original. Le point résultant sera le point terminal du « nouveau » vecteur dont le point initial est l’origine. Faites ceci pour chaque vecteur original puis comparez.
Exemple 1.2
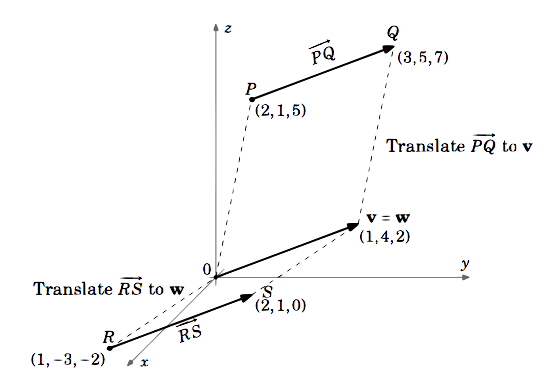
Considérez les vecteurs \(\overrightarrow{PQ}\) et \(\overrightarrow{RS}\) dans \(\mathbb{R}^{3}\), où \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\) et \(S = (2,1,0)\). Est-ce que \(\N-overrightarrow{PQ} = \N-overrightarrow{RS}\) ?
Le vecteur \(\overrightarrow{PQ}\) est égal au vecteur \(\textbf{v}\) avec le point initial \((0,0,0)\) et le point terminal \(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\).
De même, \(\overrightarrow{RS}\) est égal au vecteur \(\textbf{w}\) avec le point initial \((0,0,0)\) et le point terminal \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1, 1 – (-3),0 – (-2)) = (1,4,2)\).
Donc \(\N-overrightarrow{PQ} = \textbf{v} = (1,4,2)\) et \N-overrightarrow{RS} = \N-textbf{w} = (1,4,2)\).
\N{\i1}C’est pourquoi \N-overrightarrow{PQ} = \N-overrightarrow{RS}\)
Rappelle la formule de distance pour les points dans le plan euclidien :
Pour des points \(P = (x_{1}, y_{1})\), \(Q = (x_{2}, y_{2})\) dans \(\mathbb{R}^{2}\), la distance \(d\) entre \(P\) et \(Q\) est :
Par cette formule, nous avons le résultat suivant :
Note
Pour un vecteur \(\overrightarrow{PQ}\) dans \(\mathbb{R}^{2}\) avec un point initial \(P = (x_{1}, y_{1})\) et un point terminal \(Q = (x_{2}, y_{2})\), la valeur de \(\overrightarrow{PQ}\) est :
Trouver la magnitude d’un vecteur \(\textbf{v} = (a,b)\) dans \(\mathbb{R}^{2}\) est un cas particulier de la formule ci-dessus avec \(P = (0,0)\) et \(Q = (a,b)\) :
Pour un vecteur \(\textbf{v} = (a,b)\) dans \(\mathbb{R}^{2}\), la magnitude de \(\textbf{v}\) est :
\
Pour calculer la magnitude des vecteurs dans \(\mathbb{R}^{3}\), nous avons besoin d’une formule de distance pour les points dans l’espace euclidien (nous reporterons la preuve à la section suivante):
Théorème 1.1
La distance \(d\) entre les points \(P = (x_{1}, y_{1}, z_{1})\) et \(Q = (x_{2}, y_{2}, z_{2})\) dans \(\mathbb{R}^{3}\) est :
La preuve utilisera le résultat suivant:
Théorème 1.2
Pour un vecteur \(\textbf{v} = (a,b,c)\) dans \(\mathbb{R}^{3}\), la magnitude de \(\textbf{v}\) est:
\
Preuve : Il y a quatre cas à considérer:
\(\textit{Case 1:}\) \(a = b = c = 0\). Alors \(\N-textbf{v} = \N-textbf{0}\N), donc \N-normal{\N-textbf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}).
\(\textit{Case 2:}\) \(\textit{exactement deux de })\(a, b, c\) sont \(0\). Sans perte de généralité, nous supposons que \(a = b = 0\) et \(c \ne 0\) (les deux autres possibilités sont traitées de manière similaire). Alors \(\textbf{v} = (0,0,c)\), qui est un vecteur de longueur \(|c|\) le long de l’axe \(z\). Donc \(\norm{\textbf{v}} = | c | = \sqrt{c^{2}} = \sqrt{0^{2} + 0^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}).
\\N{\i1}Case 3:}) \(\textit{exactement un parmi })\(a, b, c\) est \(0\). Sans perte de généralité, nous supposons que \(a = 0\), \(b \ne 0\) et \(c \ne 0\) (les deux autres possibilités sont traitées de manière similaire). Alors \(\textbf{v} = (0,b,c)\), qui est un vecteur dans le plan \(yz\), donc par le théorème de Pythagore nous avons \(\norm{\textbf{v}} = \sqrt{b^{2} + c^{2}} = \sqrt{0^{2}} + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}).
\\N{\i1}Case 4:}) \N{\i1}Case 4:}) \N{\i1}A, b, c{\i}) sont \N{\i}0}. Sans perte de généralité, nous pouvons supposer que \(a, b, c\) sont tous positifs (les sept autres possibilités sont traitées de manière similaire). Considérons les points \(P = (0,0,0)\), \(Q = (a,b,c)\), \(R =(a,b,0),\) et \(S = (a,0,0)\), comme le montre la figure 1.1.8. L’application du théorème de Pythagore au triangle rectangle \(\triangle PSR\) donne \(\left\vert PR \right\vert^{2} = a^{2} + b^{2}\). Une deuxième application du théorème de Pythagore, cette fois au triangle rectangle \(\triangle PQR\), donne \(\norm{\textbf{v}} = \left\lvert PQ \right\rvert = \sqrt{\ft\vert PR \right\vert^{2} + QR = \Sqrt{a^{2} + b^{2} + c^{2}}\). Ceci prouve le théorème.
\(\tag{\(\textbf{QED}\)})
Exemple 1.3
Calculez ce qui suit :
- La grandeur du vecteur \(\overrightarrow{PQ}\) dans \(\mathbb{R}^{2}\) avec \(P = (-1,2)\) et \(Q = (5,5)\).
( \textit{Solution:}\N- Par la formule (1.2), \(\norm{\overrightarrow{PQ}} = \sqrt{(5 – (-1))^{2} + (5 – 2)^{2}} = \sqrt{36 + 9} = \sqrt{45} = 3 \sqrt{5}\). - La magnitude du vecteur \(\textbf{v} = (8,3)\) dans \(\mathbb{R}^{2}\).
\N- Par la formule (1.3), \(\norm{\textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}\). - La distance entre les points \(P = (2, -1, 4)\) et \(Q = (4, 2, -3)\) dans \(\mathbb{R}^{2}\).
\N(\textit{Solution:}\) Par la formule (1.4), la distance \(d = \sqrt{(4 – 2)^{2} + (2 – (-1))^{2} + (-3 – 4)^{2}} = \sqrt{4 + 9 + 49} = \sqrt{62}\). - La grandeur du vecteur \(\textbf{v} = (5,8,-2)\) dans \(\mathbb{R}^{3}\).
\N{\i1} Par la formule (1.5), \(\norm{\textbf{v}} = \sqrt{5^{2} + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}\).
Contributeurs et attributions
-
Michael Corral (Schoolcraft College). Le contenu de cette page est distribué selon les termes de la licence de documentation libre GNU, version 1.2.
.