11.1: Sistemas de coordenadas tridimensionales
En el cálculo de una sola variable, las funciones que uno encuentra son funciones de una variable (normalmente \(x\) o \(t\)) que varía sobre algún subconjunto de la recta numérica real (que denotamos por \(\mathbb{R}\)). Para una función de este tipo, digamos, \(y = f(x)\), el \textbf{graph}\) de la función \(f\) consiste en los puntos \((x, y) = (x, f(x))\). Estos puntos se encuentran en el plano euclidiano, que, en el sistema de coordenadas cartesianas o rectangulares, está formado por todos los pares ordenados de números reales ((a, b)). Utilizamos la palabra «euclidiano» para denotar un sistema en el que se cumplen todas las reglas habituales de la geometría euclidiana. Denotamos el plano euclidiano por \(\mathbb{R}^{2}\); el «2» representa el número de \(\textit{dimensiones}\) del plano. El plano euclidiano tiene dos ejes perpendiculares: el eje de las x y el eje de las y.
En el cálculo vectorial (o multivariable), trataremos con funciones de dos o tres variables (normalmente \N(x, y) o \N(x, y, z), respectivamente). La gráfica de una función de dos variables, por ejemplo, \(z = f(x,y)\N, se encuentra en el espacio euclidiano, que en el sistema de coordenadas cartesianas está formado por todos los triples ordenados de números reales \((a, b, c)\N.) Como el espacio euclidiano es tridimensional, lo denotamos por \mathbb{R}^{3}\). La gráfica de \(f\) está formada por los puntos \((x, y, z) = (x, y, f(x, y))\Nde). El sistema de coordenadas tridimensional del espacio euclidiano puede representarse en una superficie plana, como esta página o una pizarra, sólo dando la ilusión de tres dimensiones, de la manera mostrada en la figura 1.1.1. El espacio euclidiano tiene tres ejes de coordenadas mutuamente perpendiculares (\(x, y\) y \(z\)), y tres planos de coordenadas mutuamente perpendiculares ¡index{plano!coordenadas}: el plano \(xy\), el plano \(yz\) y el plano \(xz\) (Figura 1.1.2).
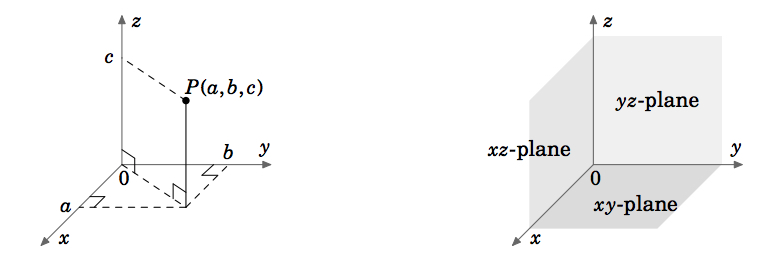
El sistema de coordenadas mostrado en la Figura 1.11 se conoce como sistema de coordenadas de la mano derecha, porque es posible, utilizando la mano derecha, apuntar con el dedo índice en la dirección positiva del eje x, con el dedo corazón en la dirección positiva del eje y y con el pulgar en la dirección positiva del eje z, como en la figura 1.1.3.
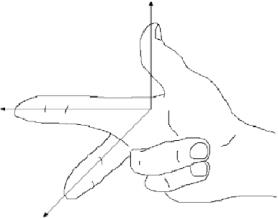
Fig 1.1.3: Sistema de coordenadas de la derecha.
Una forma equivalente de definir un sistema de la derecha es si se puede apuntar con el pulgar hacia arriba en la dirección positiva del eje \(z\) mientras se utilizan los cuatro dedos restantes para girar el eje \(x\) hacia el eje \(y). Hacer lo mismo con la mano izquierda es lo que define un sistema de coordenadas para zurdos. Obsérvese que si se cambian los ejes \(x\)- y \(y\)- en un sistema de mano derecha se obtiene un sistema de mano izquierda, y que la rotación de cualquiera de los dos tipos de sistema no cambia su «mano». A lo largo del libro utilizaremos un sistema diestro.
Para las funciones de tres variables, las gráficas existen en el espacio de 4 dimensiones (es decir, \(\mathbb{R}^{4}\)), que no podemos ver en nuestro espacio de 3 dimensiones, y mucho menos simular en el espacio de 2 dimensiones. Así que sólo podemos pensar en el espacio de 4 dimensiones de forma abstracta. Para una entretenida discusión de este tema, ver el libro de ABBOT.
Hasta ahora, hemos discutido la \ ~ (\textit{posición}\ ~) de un objeto en el espacio de 2 dimensiones o 3 dimensiones. Pero ¿qué pasa con algo como la velocidad del objeto, o su aceleración? ¿O la fuerza gravitatoria que actúa sobre el objeto? Todos estos fenómenos parecen implicar el movimiento y la dirección de alguna manera. Aquí es donde la idea de un \ (\textit{vector}\) entra en juego.
Ya has tratado con la velocidad y la aceleración en el cálculo de una sola variable. Por ejemplo, para el movimiento a lo largo de una línea recta, si \ (y = f(t)\) da el desplazamiento de un objeto después de tiempo \ (t\), entonces \ (dy/dt = f\,'(t)\) es la velocidad del objeto en el tiempo \ (t\). La derivada \(f\,'(t)\) es sólo un número, que es positivo si el objeto se mueve en una dirección «positiva» acordada, y negativo si se mueve en la dirección opuesta a esa. Así que usted puede pensar en ese número, que se llamó la velocidad del objeto, como teniendo dos componentes: un \(\textit{magnitud}\), indicado por un número no negativo, precedido por una dirección, indicado por un símbolo más o menos (que representa el movimiento en la dirección positiva o la dirección negativa, respectivamente), es decir, \(f\,'(t) = \pm a\) para algún número \(a \ge 0\). Entonces \(a\) es la magnitud de la velocidad (normalmente llamada \(\textit{velocidad}\) del objeto), y el \(\pm\) representa la dirección de la velocidad (aunque se suele omitir el \(+\) para la dirección positiva).
Para el movimiento a lo largo de una línea recta, es decir, en un espacio unidimensional, las velocidades también están contenidas en ese espacio unidimensional, ya que son sólo números. Sin embargo, para un movimiento general a lo largo de una curva en un espacio bidimensional o tridimensional, la velocidad tendrá que ser representada por un objeto multidimensional que deberá tener tanto una magnitud como una dirección. Un objeto geométrico que tiene esas características es una flecha, que en geometría elemental se llama «segmento de línea dirigido». Esta es la motivación de cómo vamos a definir un vector.
Definición 1.1
Un vector (no nulo) es un segmento de línea dirigido que va desde un punto (P) (llamado su punto inicial) a un punto (Q) (llamado su punto final), siendo P y Q distintos. El vector se denota por \(\overrightarrow{PQ}\). Su \(\textbf{magnitud}\Nes la longitud del segmento de línea, denotado por \(\norm{overrightarrow{PQ}\N), y su \N(\textbf{dirección}\Nes la misma que la del segmento de línea dirigido. El \(\textbf{vector cero}} es sólo un punto, y se denota por \(\textbf{0}}.
Para indicar la dirección de un vector, dibujamos una flecha desde su punto inicial hasta su punto terminal. A menudo denotaremos un vector con una sola letra en negrita (por ejemplo, \(\textbf{v}\)) y utilizaremos los términos «magnitud» y «longitud» indistintamente. Obsérvese que nuestra definición podría aplicarse a sistemas con cualquier número de dimensiones (Figura 1.1.4 (a)-(c)).
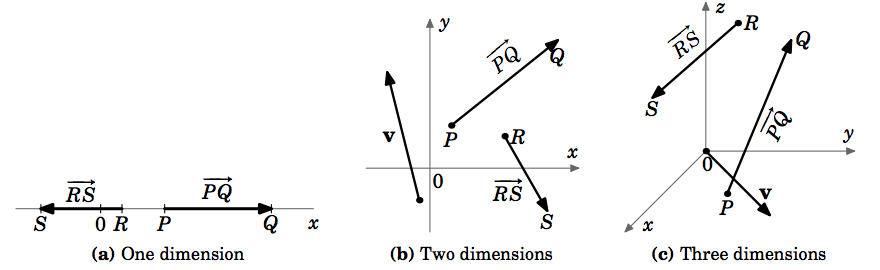
Hay que señalar algunas cosas sobre el vector cero. Nuestra motivación sobre lo que es un vector incluye las nociones de magnitud y dirección. ¿Cuál es la magnitud del vector cero? Definimos que es cero, es decir, \N (\Nnorm{textbf{0}} = 0\N). Esto concuerda con la definición del vector cero como un simple punto, que tiene longitud cero. ¿Qué pasa con la dirección del vector cero? Un solo punto realmente no tiene una dirección bien definida. Tenga en cuenta que tuvimos cuidado de definir sólo la dirección de un vector \(\textit{nonzero}\), que está bien definido ya que los puntos iniciales y terminales son distintos. No todo el mundo está de acuerdo en la dirección del vector cero. Algunos sostienen que el vector cero tiene una dirección \(\textit{arbitraria}) (es decir, puede tomar cualquier dirección), otros dicen que tiene una dirección \(\textit{indeterminada}) (es decir, la dirección no se puede determinar), mientras que otros dicen que tiene una dirección \(\textit{no}). Nuestra definición del vector cero, sin embargo, no requiere que tenga una dirección, y lo dejaremos así.
Ahora que sabemos lo que es un vector, necesitamos una forma de determinar cuándo dos vectores son iguales. Esto nos lleva a la siguiente definición.
Definición 1.2
Dos vectores no nulos son \(\textbf{equal}\) si tienen la misma magnitud y la misma dirección. Cualquier vector con magnitud cero es igual al vector cero.
Por esta definición, los vectores con la misma magnitud y dirección pero con diferentes puntos iniciales serían iguales. Por ejemplo, en la figura 1.1.5 los vectores \(\textbf{u}\), \(\textbf{v}\) y \(\textbf{w}\) tienen todos la misma magnitud \(\sqrt{5}\) (por el Teorema de Pitágoras). Y vemos que \(\textbf{u}\) y \(\textbf{w}\) son paralelas, ya que se encuentran en líneas que tienen la misma pendiente \(\frac{1}{2}\), y apuntan en la misma dirección. Por tanto, \(\textbf{u} = \textbf{w}}, aunque tengan puntos iniciales diferentes. También vemos que \(\textbf{v}\) es paralela a \(\textbf{u}\) pero apunta en la dirección opuesta. Así que \(\textbf{u} \ne \textbf{v}).
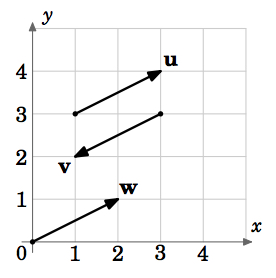
Así que podemos ver que hay un número infinito de vectores para una magnitud y dirección dadas, esos vectores son todos iguales y sólo se diferencian por sus puntos iniciales y terminales. ¿Existe un único vector que podamos elegir para representar todos esos vectores iguales? La respuesta es afirmativa, y la sugiere el vector \textbf{w} de la figura 1.1.5.
Salvo que se indique lo contrario, al hablar de «el vector» con una magnitud y dirección dadas, nos referiremos a aquel cuyo punto inicial está en el origen del sistema de coordenadas.
Pensar que los vectores parten del origen proporciona una forma de tratar los vectores de manera estándar, ya que todo sistema de coordenadas tiene un origen. Pero habrá ocasiones en las que sea conveniente considerar un punto inicial diferente para un vector (por ejemplo, al sumar vectores, lo que haremos en la siguiente sección). Otra ventaja de utilizar el origen como punto inicial es que proporciona una fácil correspondencia entre un vector y su punto terminal.
Ejemplo 1.1
Sea \(\textbf{v}\) el vector en \(\mathbb{R}^{3}\) cuyo punto inicial está en el origen y cuyo punto terminal es \((3,4,5)\N.) Aunque el \(\textit{punto}) \((3,4,5)\) y el vector \(\textbf{v}\) son objetos diferentes, es conveniente escribir \(\textbf{v} = (3,4,5)\). Al hacer esto, se entiende que el punto inicial de \(\textbf{v}} se encuentra en el origen \((0,0,0)\Ny el punto terminal es \((3,4,5)\N).
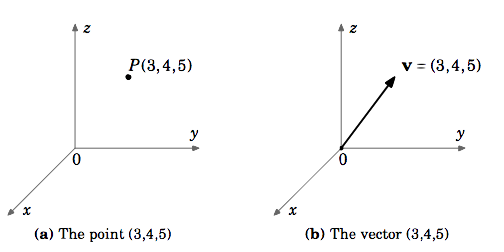
A menos que se indique lo contrario, cuando nos referimos a los vectores como \(\textbf{v} = (a,b)\Nen \Nmathbb{R}^{2}) o \Ntextbf{v} = (a,b,c)\Nen \Nmathbb{R}^{3}), nos referimos a vectores en coordenadas cartesianas que parten del origen. Además, escribiremos el vector cero \(\textbf{0}\) en \(\mathbb{R}^{2}\) y \(\mathbb{R}^{3}\) como \((0,0)\Ny \N(0,0,0)\Nrespectivamente.
La correspondencia punto-vector proporciona una manera fácil de comprobar si dos vectores son iguales, sin tener que determinar su magnitud y dirección. De forma similar a ver si dos puntos son iguales, ahora estás viendo si los puntos terminales de los vectores que parten del origen son iguales. Para cada vector, encuentra el vector (¡único!) al que equivale y cuyo punto inicial es el origen. Luego compara las coordenadas de los puntos terminales de estos «nuevos» vectores: si esas coordenadas son las mismas, entonces los vectores originales son iguales. Para obtener los «nuevos» vectores que comienzan en el origen, usted \ (\textit{translate}\) cada vector para comenzar en el origen restando las coordenadas del punto inicial original desde el punto terminal original. El punto resultante será el punto terminal del «nuevo» vector cuyo punto inicial es el origen. Haga esto para cada vector original y luego compare.
Ejemplo 1.2
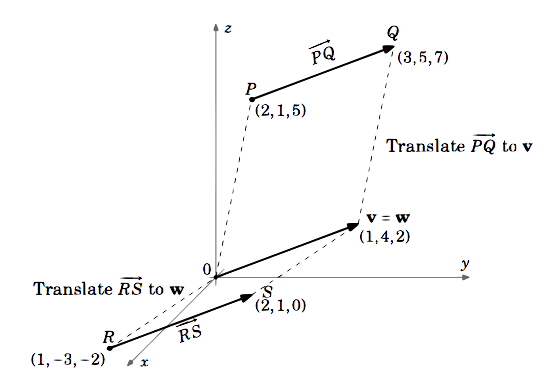
Considere los vectores \(\overrightarrow{PQ}\) y \(\overrightarrow{RS}\) en \(\mathbb{R}^{3}\), donde \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\Ny \(S = (2,1,0)\N.) ¿(\ sobre flecha{PQ} = \ sobre flecha{RS})?
El vector \(\overrightarrow{PQ}\) es igual al vector \(\textbf{v}\) con punto inicial \((0,0,0)\Ny punto terminal \N(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\N.)
De forma similar, \(\overrightarrow{RS}\) es igual al vector \(textbf{w}\) con punto inicial \((0,0,0)\) y punto terminal \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1, 1 – (-3),0 – (-2)) = (1,4,2)\N.)
Entonces \(\overrightarrow{PQ} = \textbf{v} = (1,4,2)\N- y \(\overrightarrow{RS} = \textbf{w} = (1,4,2)\N-.)
(por tanto, \ sobre flecha derecha{PQ} = \ sobre flecha derecha{RS})
Recordemos la fórmula de la distancia para puntos en el plano euclidiano:
Para los puntos \(P = (x_{1}, y_{1})\N), \(Q = (x_{2}, y_{2})\Nen \N(\mathbb{R}^{2}), la distancia \N(d\N) entre \N(P\N) y \N(Q\N) es:
\
Por esta fórmula, tenemos el siguiente resultado:
Nota
Para un vector \(\overrightarrow{PQ}\) en \(\mathbb{R}^{2}) con punto inicial \(P = (x_{1}, y_{1})\Ny el punto terminal \N(Q = (x_{2}, y_{2})\Ncon la magnitud de \N(\overrightarrow{PQ}\Nes:
\
Hallar la magnitud de un vector \(\textbf{v} = (a,b)\) en \(\mathbb{R}^{2}\) es un caso especial de la fórmula anterior con \(P = (0,0)\) y \(Q = (a,b)\N:)
Para un vector \(\textbf{v} = (a,b)\) en \(\mathbb{R}^{2}\), la magnitud de \(\textbf{v}\) es:
\Npara calcular la magnitud de los vectores en \N(\mathbb{R}^{3}\Nnecesitamos una fórmula de distancia para puntos en el espacio euclidiano (pospondremos la demostración hasta el siguiente apartado):
Teorema 1.1
La distancia \(d\) entre los puntos \(P = (x_{1}, y_{1}, z_{1})\ y \(Q = (x_{2}, y_{2}, z_{2})\) en \(\mathbb{R}^{3}\) es:
\
La prueba utilizará el siguiente resultado:
Teorema 1.2
Para un vector \(\textbf{v} = (a,b,c)\Nen \N(\mathbb{R}^{3}\N), la magnitud de \N(\textbf{v}\Nes:
Prueba: Hay cuatro casos a considerar:
(\textit{caso 1:}\) \(a = b = c = 0\). Entonces \(\textbf{v} = \textbf{0}\), por lo que \(\norm{{textbf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}.
(\textit{Caso 2:}\) \(\textit{exactamente dos de }\)\N-(a, b, c\) son \N-(0\). Sin pérdida de generalidad, suponemos que \(a = b = 0\) y \(c \ne 0\) (las otras dos posibilidades se manejan de manera similar). Entonces \(\textbf{v} = (0,0,c)\Nes un vector de longitud \(|c|\) a lo largo del eje \(z\). Así que \(\norm{textbf{v}} = | c | = \sqrt{c^{2}} = \sqrt{0^{2} + 0^{2} + c^{2}} = \sqrt{a^{2}} + b^{2} + c^{2}}.
(\textit{caso 3:}\) \(\textit{exactamente uno de})\N-(a, b, c\) es \N-(0\). Sin pérdida de generalidad, suponemos que \(a = 0\), \(b \ne 0\) y \(c \ne 0\) (las otras dos posibilidades se manejan de manera similar). Entonces \(\textbf{v} = (0,b,c)\Nes un vector en el plano \N(yz\), por lo que por el Teorema de Pitágoras tenemos que \Nla norma{textbf{v}} = \sqrt{b^{2} + c^{2}} = \sqrt{0^{2} + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}.
(\textit{caso 4:}\) \(\textit{nada de})\N-(a, b, c\) son \N(0\). Sin pérdida de generalidad, podemos suponer que \(a, b, c\) son todos positivos (las otras siete posibilidades se manejan de manera similar). Consideremos los puntos \(P = (0,0,0)\N, \(Q = (a,b,c)\N, \(R =(a,b,0),\Ny \N(S = (a,0,0)\Ncomo se muestra en la figura 1.1.8. Aplicando el Teorema de Pitágoras al triángulo rectángulo \(\triángulo PSR\) se obtiene \(\left\vert PR \right\vert^{2} = a^{2} + b^{2}\). Una segunda aplicación del Teorema de Pitágoras, esta vez al triángulo rectángulo PQR, da como resultado que (\norm{textbf{v}} = \left\lvert PQ \right\rvert = \sqrt{left\vert PR \right\vert^{2} + \left\vert QR \right\vert^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}\). Esto demuestra el teorema.
(\tag{{(\textbf{QED})})
Ejemplo 1.3
Calcule lo siguiente:
- La magnitud del vector \(\overrightarrow{PQ}\) en \(\mathbb{R}^{2}\) con \(P = (-1,2)\N y \(Q = (5,5)\N.)
( \textit{Solución:}} Por la fórmula (1.2), \(\norm{overrightarrow{PQ}} = \sqrt{(5 – (-1))^{2} + (5 – 2)^{2}} = \sqrt{36 + 9} = \sqrt{45} = 3 \sqrt{5}). - La magnitud del vector (\textbf{v} = (8,3)\s en \mathbb{R}^{2}}.
(\textit{Solución:}) Por la fórmula (1.3), \norm{textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}}. - La distancia entre los puntos \(P = (2, -1, 4)\Ny \(Q = (4, 2, -3)\Nen \(\mathbb{R}^{2}).
(\textit{Solución:}) Por la fórmula (1.4), la distancia \(d = \sqrt{(4 – 2)^{2} + (2 – (-1))^{2} + (-3 – 4)^{2}} = \sqrt{4 + 9 + 49} = \sqrt{62}\). - La magnitud del vector \(\textbf{v} = (5,8,-2)\) en \(\mathbb{R}^{3}\).
(\textit{Solución:}) Por la fórmula (1.5), (\norm{textbf{v}} = \sqrt{5^{2} + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}).
Contribuidores y Atribuciones
-
Michael Corral (Schoolcraft College). El contenido de esta página se distribuye bajo los términos de la licencia de documentación libre de GNU, versión 1.2.