11.1: Driedimensionale coordinatenstelsels
In de enkel-variabele wiskunde zijn de functies die men tegenkomt functies van een variabele (meestal x(x) of t(t)) die varieert over een deelverzameling van de reële getallenlijn (die we aanduiden met \(\mathbb{R}\)). Voor zo’n functie, bijvoorbeeld y = f(x), bestaat de grafiek van de functie uit de punten x, y = (x, f(x))\). Deze punten liggen in het Euclidisch vlak, dat in het cartesisch of rechthoekig coördinatenstelsel bestaat uit alle geordende paren van reële getallen (a, b). We gebruiken het woord `Euclidisch’ om een systeem aan te duiden waarin alle gebruikelijke regels van de Euclidische meetkunde gelden. Het Euclidische vlak duiden we aan met `(\mathbb{R}^{2}}); de `”2” staat voor het aantal \(\textit{dimensies}}) van het vlak. Het vlak van Euclides heeft twee loodrecht op elkaar staande assen: de x-as en de y-as.
In de vectorrekening (of multivariabele wiskunde) behandelen we functies van twee of drie variabelen (meestal respectievelijk x, y of x, y, z). De grafiek van een functie van twee variabelen, bijvoorbeeld z = f(x,y)ligt in de euclidische ruimte, die in het cartesisch coordinatensysteem bestaat uit alle geordende drievouden van reële getallen ((a, b, c)). Omdat de euclidische ruimte 3-dimensionaal is, duiden we haar aan met \(\mathbb{R}^{3}\). De grafiek van \(f) bestaat uit de punten \((x, y, z) = (x, y, f(x, y))\). Het driedimensionale coördinatenstelsel van de euclidische ruimte kan op een plat vlak, zoals deze bladzijde of een schoolbord, alleen worden voorgesteld door de illusie van drie dimensies te wekken, op de manier die is weergegeven in figuur 1.1.1. De euclidische ruimte heeft drie onderling loodrechte coördinatenassen (x, y en z), en drie onderling loodrechte coördinatenvlakken: de vlakke!coördinaten}: het xy-vlak, het yz-vlak en het xz-vlak (figuur 1.1.2).
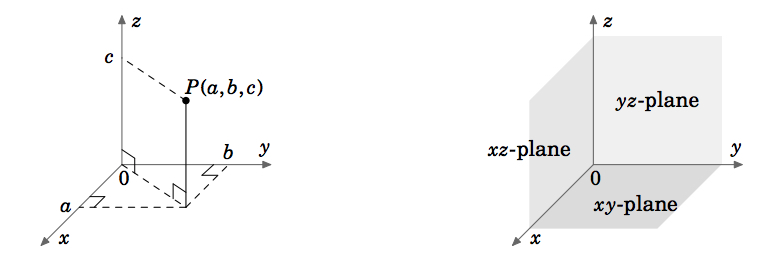
Het coördinatenstelsel in figuur 1.1.1 staat bekend als een xy-vlak en een yz-vlak.1 staat bekend als een rechtshandig coördinatenstelsel, omdat het mogelijk is om met de rechterhand de wijsvinger in de positieve richting van de x-as te wijzen, de middelvinger in de positieve richting van de y-as en de duim in de positieve richting van de z-as, zoals in figuur 1.1.3.
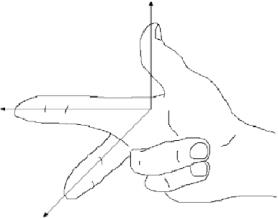
Figuur 1.1.3: Rechtshandig coördinatenstelsel.
Een gelijkwaardige manier om een rechtshandig stelsel te definiëren is als je met je duim omhoog kunt wijzen in de positieve richting van de z-as, terwijl je met de overige vier vingers de x-as roteert in de richting van de y-as. Hetzelfde doen met de linkerhand is wat een linkshandig coördinatenstelsel definieert. Merk op dat het verwisselen van de x-as en de y-as in een rechtshandig stelsel resulteert in een linkshandig stelsel, en dat het roteren van beide typen stelsels de “handigheid” niet verandert. In het hele boek zullen we een rechtshandig stelsel gebruiken.
Voor functies van drie variabelen bestaan de grafieken in de 4-dimensionale ruimte (d.w.z. \(\mathbb{R}^{4}\)), die we in onze 3-dimensionale ruimte niet kunnen zien, laat staan simuleren in de 2-dimensionale ruimte. We kunnen dus alleen abstract denken aan de 4-dimensionale ruimte. Voor een onderhoudende bespreking van dit onderwerp, zie het boek van ABBOT.
Tot nu toe hebben we het gehad over de positie van een voorwerp in de 2-dimensionale of 3-dimensionale ruimte. Maar hoe zit het met iets als de snelheid van het voorwerp, of de versnelling? Of de gravitatiekracht die op het voorwerp werkt? Al deze verschijnselen lijken op de een of andere manier met beweging en richting te maken te hebben. Hier komt het idee van een vector om de hoek kijken. Je hebt al te maken gehad met snelheid en versnelling in enkel-variabele calculus. Bijvoorbeeld, voor een beweging langs een rechte lijn, als \(y = f(t)\) de verplaatsing van een voorwerp na tijd \(t) geeft, dan is \(dy/dt = f(t)\) de snelheid van het voorwerp op tijd \(t). De afgeleide is gewoon een getal, dat positief is als het object beweegt in een afgesproken “positieve” richting, en negatief als het beweegt in de tegengestelde richting van die richting. Je kunt dat getal, dat de snelheid van het voorwerp werd genoemd, dus opvatten als bestaande uit twee componenten: een getal dat wordt aangegeven met een niet-negatief getal, voorafgegaan door een richting, die wordt aangegeven met een plus- of minteken (dat staat voor beweging in de positieve richting, respectievelijk de negatieve richting), d.w.z. f(t) = pm a voor een getal dat wordt aangegeven met a 0. Dan is (a) de grootte van de snelheid (gewoonlijk de snelheid van het voorwerp genoemd), en geeft (pm) de richting van de snelheid aan (hoewel (+) meestal wordt weggelaten voor de positieve richting).
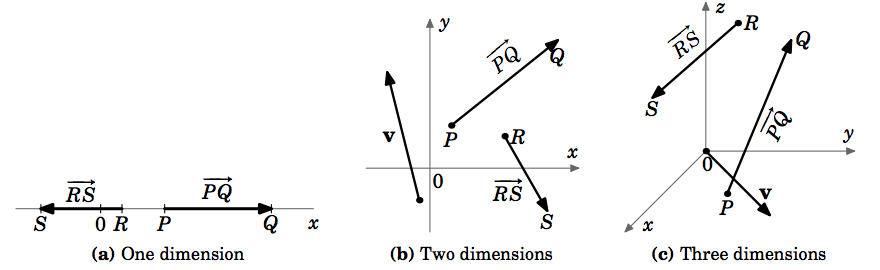
Voor beweging langs een rechte lijn, dus in een eendimensionale ruimte, liggen de snelheden ook in die eendimensionale ruimte, want het zijn gewoon getallen. Voor een algemene beweging langs een kromme in de 2- of 3-dimensionale ruimte moet de snelheid echter worden voorgesteld door een meerdimensionaal object dat zowel een magnitude als een richting moet hebben. Een meetkundig object dat deze eigenschappen heeft is een pijl, die in de elementaire meetkunde een “gericht lijnstuk” wordt genoemd. Dit is de motivatie voor hoe we een vector zullen definiëren.
Definitie 1.1
Een (niet nul) vector is een gericht lijnstuk, getrokken van een punt P (genoemd zijn beginpunt) naar een punt Q (genoemd zijn eindpunt), waarbij P en Q verschillende punten zijn. De vector wordt aangeduid met \(PQ}). De lengte van de vector is gelijk aan de lengte van het lijnstuk, aangeduid met \norm{overrightarrow{PQ}}}, en de lengte is gelijk aan de lengte van het gerichte lijnstuk. De (\textbf{nulvector}} is gewoon een punt, en wordt aangeduid met \(\textbf{0}}).
Om de richting van een vector aan te geven, tekenen we een pijl van zijn beginpunt naar zijn eindpunt. We zullen een vector vaak aanduiden met één vetgedrukte letter (b.v. \(\textbf{v}\)) en de termen “magnitude” en “lengte” door elkaar gebruiken. Merk op dat onze definitie van toepassing kan zijn op stelsels met een willekeurig aantal dimensies (figuur 1.1.4 (a)-(c)).
Een paar dingen moeten worden opgemerkt over de nulvector. Onze motivatie voor wat een vector is, omvatte de begrippen magnitude en richting. Wat is de magnitude van de nulvector? We definiëren hem als nul, d.w.z. Dit komt overeen met de definitie van de nulvector als gewoon een punt, dat lengte nul heeft. Hoe zit het met de richting van de nulvector? Een enkel punt heeft echt geen welbepaalde richting. Merk op dat we voorzichtig zijn geweest om alleen de richting van een nulvector te definiëren, die goed gedefinieerd is omdat de begin- en eindpunten verschillend zijn. Niet iedereen is het eens over de richting van de nulvector. Sommigen beweren dat de nulvector een willekeurige richting heeft, anderen zeggen dat hij een onbepaalde richting heeft, terwijl weer anderen zeggen dat hij geen bepaalde richting heeft. Onze definitie van de nulvector vereist echter niet dat hij een richting heeft, en we zullen het daarbij laten.
Nu we weten wat een vector is, hebben we een manier nodig om te bepalen wanneer twee vectoren gelijk zijn. Dit leidt ons tot de volgende definitie.
Definitie 1.2
Twee niet nulvectoren zijn gelijk als ze dezelfde magnitude en dezelfde richting hebben. Elke vector met nulmagnitude is gelijk aan de nulvector.
Volgens deze definitie zouden vectoren met dezelfde magnitude en richting maar met verschillende beginpunten gelijk zijn. Bijvoorbeeld, in figuur 1.1.5 hebben de vectoren \(\textbf{u}}, \(\textbf{v}}) en \(\textbf{w}}) allemaal dezelfde magnitude \(\sqrt{5}}) (door de Stelling van Pythagoras). En we zien dat \(\textbf{u}}) en \(\textbf{w}}) evenwijdig zijn, omdat ze op lijnen liggen met dezelfde helling \(\frac{1}{2}}), en ze wijzen in dezelfde richting. Dus \(\textbf{u} = \textbf{w}}), ook al hebben ze verschillende beginpunten. We zien ook dat \textbf{v}} evenwijdig is aan \textbf{u}}, maar in de tegengestelde richting wijst. We zien dus dat \(\textbf{u}) evenwijdig is aan \(\textbf{v}).
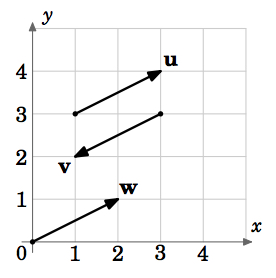
Zo zien we dat er oneindig veel vectoren zijn voor een gegeven grootte en richting, dat die vectoren allemaal gelijk zijn en alleen verschillen door hun begin- en eindpunten. Is er een enkele vector die we kunnen kiezen om al die gelijke vectoren weer te geven? Het antwoord is ja en wordt gesuggereerd door de vector in figuur 1.1.5.
Tenzij anders is aangegeven, bedoelen we met “de vector” met een gegeven grootte en richting, de vector waarvan het beginpunt in de oorsprong van het assenstelsel ligt.
Doordacht dat vectoren vertrekken vanuit de oorsprong, biedt een manier om op een standaardmanier met vectoren om te gaan, aangezien elk coordinatenstelsel een oorsprong heeft. Maar er zullen momenten zijn waarop het handig is om een ander beginpunt voor een vector te nemen (bijvoorbeeld bij het optellen van vectoren, wat we in de volgende sectie zullen doen). Een ander voordeel van het gebruik van de oorsprong als beginpunt is dat het een gemakkelijke overeenkomst oplevert tussen een vector en zijn eindpunt.
Voorbeeld 1.1
Zij \(\textbf{v}\) de vector in \(\mathbb{R}^{3}\) waarvan het beginpunt bij de oorsprong ligt en waarvan het eindpunt \((3,4,5)\) is. Hoewel het beginpunt en de vector verschillende objecten zijn, is het handig om te schrijven dat het beginpunt en de vector verschillende objecten zijn. Hierbij wordt ervan uitgegaan dat het beginpunt van (\textbf{v}) op de oorsprong ligt en het eindpunt op \(3,4,5)\).
Tenzij anders vermeld, wanneer we vectoren aanduiden als \(\bf{v} = (a,b) in \(\mathbb{R}^{2}}) of \(\textbf{v} = (a,b,c)\) in \(\mathbb{R}^{3}}) vectoren noemen, dan bedoelen we vectoren in cartesische coördinaten, beginnend bij de oorsprong. Ook zullen we de nulvector in \(\mathbb{R}^{2}}) en \(\mathbb{R}^{3}}) schrijven als respectievelijk \((0,0)\) en \((0,0,0)\).
De punt-vector overeenkomst biedt een gemakkelijke manier om te controleren of twee vectoren gelijk zijn, zonder dat je hun magnitude en richting hoeft te bepalen. Net zoals je kijkt of twee punten gelijk zijn, kijk je nu of de eindpunten van vectoren die bij de oorsprong beginnen gelijk zijn. Zoek voor elke vector de (unieke!) vector waaraan hij gelijk is en waarvan het beginpunt de oorsprong is. Vergelijk dan de coordinaten van de eindpunten van deze “nieuwe” vectoren: als die coordinaten gelijk zijn, dan zijn de oorspronkelijke vectoren gelijk. Om de “nieuwe” vectoren te krijgen die in de oorsprong beginnen, trek je van elke vector de coördinaten van het oorspronkelijke beginpunt af van het oorspronkelijke eindpunt. Het resulterende punt wordt het eindpunt van de “nieuwe” vector waarvan het beginpunt de oorsprong is. Doe dit voor elke oorspronkelijke vector en vergelijk dan.
Voorbeeld 1.2
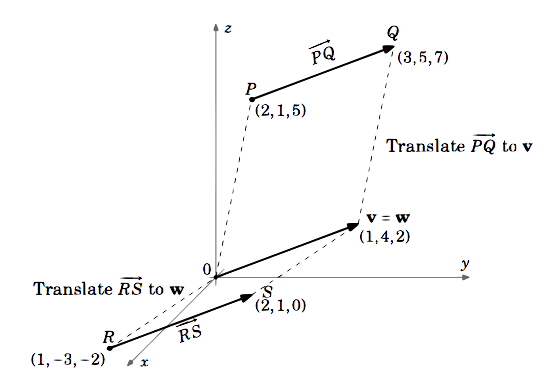
Bekijk de vectoren \(\overrightarrow{PQ}}) en \(\overrightarrow{RS}}) in \(\mathbb{R}^{3}}), waarin \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\) en \(S = (2,1,0)\). Is dat zo?
De vector (\overrightarrow{PQ}}) is gelijk aan de vector \(\textbf{v}}) met beginpunt \((0,0,0)\) en eindpunt \(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\).
Ook is (\overrightarrow{RS}) gelijk aan de vector \(\textbf{w}) met beginpunt \((0,0,0)\) en eindpunt \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1, 1 – (-3),0 – (-2)) = (1,4,2)\).
Dus \(\overrightarrow{PQ} = \textbf{v} = (1,4,2)\) en \(\overrightarrow{RS} = \textbf{w} = (1,4,2)\).
(dus \overrightarrow{PQ} = \overrightarrow{RS}})
Herhaal de afstandsformule voor punten in het euclidische vlak:
Voor punten \(P = (x_{1}, y_{1})\), \(Q = (x_{2}, y_{2})\) in \(\mathbb{R}^{2}}), is de afstand \(d\) tussen \(P\) en \(Q\):
Met deze formule hebben we het volgende resultaat:
Noot
Voor een vector \(\overrightarrow{PQ}}) in \(\mathbb{R}^{2}}) met beginpunt \(P = (x_{1}, y_{1})\) en eindpunt \(Q = (x_{2}, y_{2})\), is de grootte van \(\overrightarrow{PQ}}):
De bepaling van de grootte van een vector \(\textbf{v} = (a,b)\) in \(\mathbb{R}^{2}}) is een speciaal geval van de bovenstaande formule met \(P = (0,0)\) en \(Q = (a,b)\):
Voor een vector \(\textbf{v} = (a,b)\) in \(\mathbb{R}^{2}}), is de grootte van \(\textbf{v}}):
Om de grootte van vectoren in \(\mathbb{R}^{3}}) te berekenen, hebben we een afstandsformule nodig voor punten in de euclidische ruimte (het bewijs stellen we uit tot het volgende hoofdstuk):
Stelling 1.1
De afstand \(d) tussen punten \(P = (x_{1}, y_{1}, z_{1})\) en \(Q = (x_{2}, y_{2}, z_{2})\) in \(\mathbb{R}^{3}}) is:
Het bewijs zal gebruik maken van het volgende resultaat:
Stelling 1.2
Voor een vector \(\textbf{v} = (a,b,c)\) in \(\mathbb{R}^{3}}) is de grootte van \(\textbf{v}):
Het bewijs: Er zijn vier gevallen te beschouwen:
(\textbf{v}:}) \(a = b = c = 0). Dan geldt \(\textbf{v} = \textbf{0}}), dus \(\norm{textbf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}.
(^textit{geval 2:}}) ^(^textit{exact twee van }})^(a, b, c}} zijn ^{0}}. Zonder verlies van algemeenheid nemen we aan dat a = b = 0) en c = 0) (de andere twee mogelijkheden worden op dezelfde manier behandeld). Dan is \(\textbf{v} = (0,0,c)\) een vector van lengte \(|c|) langs de \(z)-as. Dus \norm{textbf{v}} = | c | = \sqrt{c^{2}} = \sqrt{0^{2} + 0^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}.
(a, b, c) is ^{0}}. Zonder verlies van algemeenheid nemen we aan dat a = 0, b gelijk is aan 0 en c gelijk is aan 0 (de andere twee mogelijkheden worden op dezelfde manier behandeld). Dan is \(\textbf{v} = (0,b,c)\), wat een vector in het yz-vlak is, dus door de stelling van Pythagoras hebben we \(\norm{textbf{v}} = \sqrt{b^{2} + c^{2}} = \sqrt{0^{2} + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}.
(a, b, c) zijn \(0). Zonder verlies van algemeenheid kunnen we aannemen dat \(a, b, c) allemaal positief zijn (de andere zeven mogelijkheden worden op een vergelijkbare manier behandeld). Beschouw de punten P = (0,0,0), Q = (a,b,c), R = (a,b,0) en S = (a,0,0), zoals weergegeven in figuur 1.1.8. Toepassing van de Stelling van Pythagoras op de rechthoekige driehoek PSR geeft \(R =(a,b,0)\) en \(S =(a,0,0)\). Een tweede toepassing van de stelling van Pythagoras, dit keer op de rechthoekige driehoek PQR, geeft \(\linksomkeren PQ) = \rechtsomkeren PQ = \sqrt{linksomkeren PR \rechtsomkeren^{2} + \linksomkeren QR = a^{2} + b^{2}). + \left QR \levert^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}\). Dit bewijst de stelling.
(\tag{(\textbf{QED})})
Voorbeeld 1.3
Bereken het volgende:
- De grootte van de vector (\overrightarrow{PQ}}) in \(\mathbb{R}^{2}}) met \(P = (-1,2)\) en \(Q = (5,5)\).
- De grootte van de vector \(\textbf{v} = (8,3)\) in \(\mathbb{R}^{2}}).
Volgens formule (1.3) is \(\norm{textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}}).- De afstand tussen de punten (P = (2, -1, 4)\) en \(Q = (4, 2, -3)\) in \(\mathbb{R}^{2}}.
(\textit{Oplossing:}\) Volgens formule (1.4) is de afstand \(d = \sqrt{(4 – 2)^{2} + (2 – (-1))^{2} + (-3 – 4)^{2}} = \sqrt{4 + 9 + 49} = \sqrt{62}).- De grootte van de vector \(\textbf{v} = (5,8,-2)\) in \(\mathbb{R}^{3}}).
(\textit{Oplossing:}) Volgens formule (1.5) is \(\norm{\textbf{v}} = \sqrt{5^{2} + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}}). - De grootte van de vector \(\textbf{v} = (8,3)\) in \(\mathbb{R}^{2}}).
Bijdragers en toeschrijvingen
-
Michael Corral (Schoolcraft College). De inhoud van deze pagina wordt verspreid onder de voorwaarden van de GNU Free Documentation License, Version 1.2.