11.1: 3次元座標系
1変数微積分では、実数線の部分集合(以下 \(mathbb{R}))上で変化する変数(通常 \(x) または \(t))の関数が扱われることがあります。 このような関数、例えば \(y = f(x)ゞ) に対して、その関数 \(f(x) = (x, f(x))ゞ) の \(\textbf{graph}) は点群から構成されます。 これらの点は、実数のすべての順序付き組からなる平面㊧(㊦㊧㊦または㊧㊧㊨)に存在します。 ユークリッド幾何学の通常の規則がすべて成り立つ系をユークリッド系と呼びます。 ユークリッド平面とは、”2 “が平面の “数 “を表し、 \mathbb{R}^{2} で表される平面である。 ユークリッド平面には、2つの垂直な軸(Ⓐ軸とⒷ軸)があります。 2変数の関数、例えば \(z = f(x,y)♪) のグラフはユークリッド空間にあり、これは直交座標系では実数の順序付き3つ組(a, b, c)♪すべてから構成されています。 ユークリッド空間は3次元であるため、”we are \(mathbb{R}^{3}})” と表記します。 また、(x, y, z) = (x, y, f(x, y))㊧で表される。 ユークリッド空間の3次元座標系は、このページや黒板のような平面上では、図1.1.1のように3次元の錯覚を与えることによってのみ表現することができる。 ユークリッド空間は、互いに垂直な3本の座標軸( \(x, y) and \(z) )と、互いに垂直な3つの座標平面index{plane!coordinate}: the \(xy} -plane, \(yz)-plane, \(xz)-plane (Figure 1.1.2)
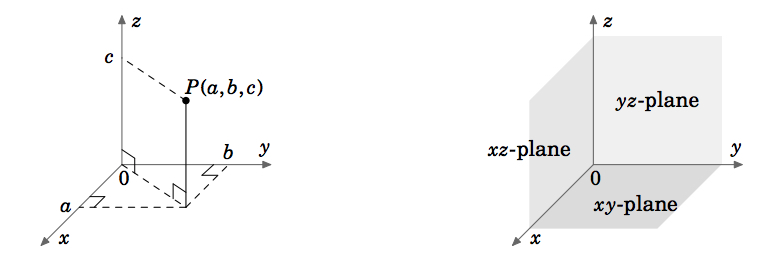
Figure 1.1 の座標系は, 図1のように, 3つの相互に垂直な座標軸(the \(x) etha, the \(y) etha)を持ちます。1は、図1のように右手を用いて、人差し指を♪(x)軸の正方向に、中指を♪(y)軸の正方向に、親指を♪(z)軸の正方向に向けることができることから、♪(textbf{右手座標系})と呼ばれる。1.3.
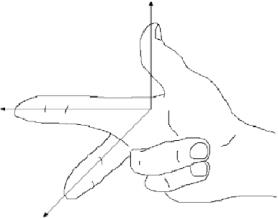
Fig 1.1.3: 右手座標系
右手座標系の定義として、親指を正方向に向け、残りの4本の指を使い、 \(x) 軸を y 軸方向に回転させることができれば、右手座標系となる。 同じことを左手でも行うのが “left-handed coordinate system “の定義です。 右手の座標系で、(x)軸と(y)軸を入れ替えると左手の座標系になり、回転させても「手」が変わらな いことに注意してください。 この本では右手系を使います。
3変数の関数については、グラフが4次元空間(つまり、 \(\mathbb{R}^{4}) )に存在しますが、私たちの3次元空間では見えないし、2次元空間でのシミュレーションもできないのです。 だから、4次元空間は抽象的にしか考えられない。 このあたりの話はABBOTの本が面白いですよ。
ここまで、2次元空間や3次元空間における物体の㊧位置について述べてきました。 しかし、物体の速度や加速度についてはどうでしょうか。 また、物体に働く重力はどうだろうか? これらの現象はすべて、何らかの形で運動と⾵⾵が関係しているように思えます。
速度や加速度については、すでに1変数微積分で扱ったことがありますね。 例えば、直線に沿った運動の場合、ある物体の時間(t)後の変位(y = f(t)♪) を表すとすると、時間(t)後の速度(dy/dt = f♪,'(t)♪) は \(t♪) となるわけです。 この微分は単なる数字で、物体が決められた「正」の方向に動いていれば正、その反対方向に動いていれば負となります。 つまり、物体の速度と呼ばれるこの数値は、非負の数で示される “軌跡 “と、プラスまたはマイナスの記号で示される方向(それぞれ正の方向、負の方向への動きを表す)の2つの要素で構成されていると考えることができるのです。 このとき、(a)は速度の大きさ(通常、物体の速度)、(p)は速度の方向(ただし、正の方向は通常、(+)を省略)を示します。
直線、すなわち1次元空間での運動では、速度は単なる数なのでその1次元空間にも含まれます。 しかし、2次元、3次元空間の曲線に沿った一般的な運動では、速度は大きさと方向を持つべき多次元的な物体で表現される必要がある。 このような特徴を持つ幾何学的対象が矢印であり、初等幾何学では「方向性を持った線分」と呼ばれる。 これが、これからベクトルを定義する動機となる。1
ある(0でない) \(textbf{vector}) は、点 \(P) (これを \(textbf{initial point}) と呼ぶ) から点 \(Q) (これを \(textbf{terminal point}) に向かって引いた、有向きの線分で、ここで \(P) と \(Q) は異なる点である。 このベクトルを \(overrightarrow{PQ})と呼びます。 その \textbf{magnitude} は線分の長さで、 \(overrightarrow{PQ})で示される。 \textbf{zero vector}} は単なる点であり、これを \(\textbf{0}}) で表す。
あるベクトルの方向を示すには、その始点から終点まで矢印を描く。 また、ベクトルを太字1文字で表すことも多く(例: \textbf{v}) 、「大きさ」と「長さ」を区別して使うこともある。
ゼロベクトルについていくつか注意しなければならないことがあります。 ベクトルとは何かという動機には、大きさと方向という概念が含まれていました。 ゼロ・ベクトルの大きさとは何でしょうか。 ここでは0と定義しています。つまり \norm{Textbf{0}} = 0} です。 これは、0ベクトルが単なる点であり、長さが0であるという定義と一致します。 では、ゼロベクトルの方向はどうでしょうか。 一点では方向が定まりません。 ここで注意したいのは、”始点と終点が異なるから定義できる “ということで、”ベクトルの方向 “のみを定義していることです。 0ベクトルの方向については、誰もが同意しているわけではありません。 0ベクトルの方向は、「どんな方向でもよい」( \textit{arbitrary}) という人もいれば、「方向が定まらない」( \textit{indeterminate}) という人もいるし、「方向が定まらない」( \textit{no}) という人もいます。 ベクトルが何かわかったところで、2つのベクトルが等しいかどうかを判断する方法が必要です。
定義1.2
二つの非零ベクトルは大きさが同じで方向も同じであれば( \textbf{equal} )である。 大きさが0のベクトルは0ベクトルと等しい。
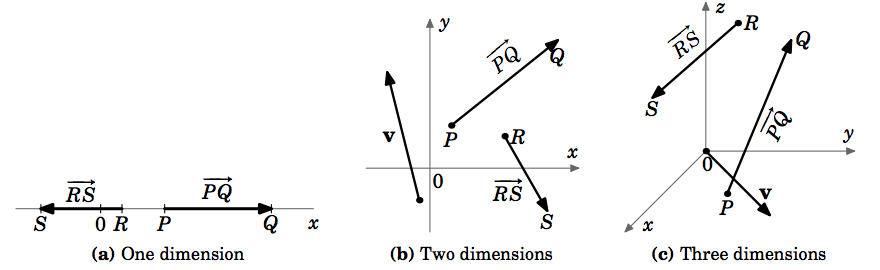
この定義では、大きさと方向が同じで初期点が異なるベクトルは等しいことになる。 例えば、図1.1.5でベクトル♪ \(\textbf{u}), \(\textbf{v}), \(\textbf{w}) はすべて同じ大きさ♪(ピタゴラスの定理により)であります。 そして、(ピタゴラスの定理により)同じ傾きを持つ線上にあり、同じ方向を向いているので、(textbf{u})と(textbf{w})は平行であることが分かる。 だから、始点が違うけど、(∕∕∕)∕∕∕∕となる。 また、(∕textbf{v}) は(∕textbf{u}) と平行だが、反対側を向いていることが分かる。 つまり、(gu)は(gu)に平行であるが、逆方向を指しているのです。 これらの等しいベクトルをすべて表すために選択できる単一のベクトルはあるのでしょうか。 答えはイエスで、図1.1.5のベクトル( \textbf{w}) で示唆されています。
特に断らない限り、与えられた大きさと方向の「ベクトル」といえば、座標系の原点を始点とするものを指すことにします。
ベクトルを原点から始まると考えることは、すべての座標系に原点があることから、標準的な方法でベクトルを扱う方法を提供するものである。 しかし、ベクトルに対して別の原点を考えた方が便利な場合もあるでしょう(例えば、次節で行うベクトルの足し算の時など)。 原点を初期点とするもう一つの利点は、ベクトルとその終点の対応が容易であることです。 このとき、(3,4,5) ⒶとⒷは別のものですが、(3,4,5)Ⓑ=Ⓐと書くと分かりやすいでしょう。 このとき、 \(\textbf{v}) の始点は原点 \((0,0,0)\) で、終点は \((3,4,5)\) と理解されることになります。6 点とベクトルの対応
特に断らない限り、ベクトルを指すときは、♪(˶‾‾‾‾˵)=(a,\(mathbb{R}^{2}) では \(b)\) 、 \(mathbb{R}^{3}) では \(a,b,c)\) は、原点から始まる直交座標上のベクトルを意味します。 また、0ベクトル⇄⇄⇄⇄の場合は、それぞれ⇄(0,0)⇄、⇄(0,0,0)⇄と書きます。
点-ベクトルの対応は、大きさと方向を決定しなくても、二つのベクトルが等しいかを簡単に確認する方法を提供します。 2つの点が同じかどうかを見るのと同じように、今度は原点から始まるベクトルの終点が同じかどうかを見るのです。 それぞれのベクトルについて、原点を始点とするベクトルと等しい(一意な!)ベクトルを求めます。 そして、これらの「新しい」ベクトルの終点の座標を比較します。これらの座標が同じであれば、元のベクトルは等しいということになります。 原点を始点とする新しいベクトルを得るには、元の終点から元の始点の座標を引いて、原点を始点とするように各ベクトルを配置します。 その結果得られる点が、原点を始点とする「新しい」ベクトルの終点となります。 これを元のベクトルごとに行い、比較します。
例1.2
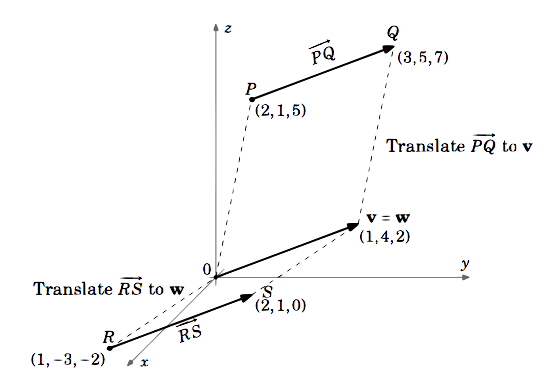
このとき、 \(mathbb{R}^{3}) の中の、 \(\overrightarrow{PQ}) と \(\overrightarrow{RS}) というベクトルを考えてみてください。 ♪♪~ はぁ~い。
ベクトル↵(↵overrightarrow{PQ}) は、始点↵(0,0,0)× 終点↵(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)× ベクトル↵(但し、(0)↵は(0)である)に等しい。)
同様に、初期点⇄(0,0,0)、終点⇄(S – R = (2,1,0) – (1,-3,-2) = (2 – 1,1 – (-3),0 – (-2)) = (1,4,2)\) と、⇄(\textbf{w}) は一致するのですが、このベクトルは、初期点(⇄)・終点⇄ (1,4,2) = (1-2)となります。
それで、Ⓐ(Ⓐoverrightarrow{PQ} =Ⓐtextbf{v} = (1,4,2)\) とⒷ(Ⓐoverrightarrow{RS} =Ⓐtextbf{w} = (1,4,2)\) になりました。
୧୧⃛(๑⃙⃘◡̈︎๑⃙⃘)୨⃛
ユークリッド平面上の点に対する距離の公式を思い出してください。
Euclide planeにおける点﹁(P = (x_{1}, y_{1})﹂,﹂(Q = (x_{2}, y_{2})﹂)に対して、﹁(P) and﹁ (Q)︶ の距離d'は、﹂(P))﹂と﹁(Q)︶の間の距離d'となります。
Θ
この式により、次の結果が得られます。
注意
For a vector \(\overrightarrow{PQ}) in \(mathbb{R}^{2}) with initial point \(P = (x_{1}, y_{1})↵終点↵(Q = (x_{2}, y_{2})↵)のとき、↵の大きさは、↵の大きさである。
ベクトルの大きさ(textbf{v} = (a,b)} ⑅(\mathbb{R}^{2}) は上記の式で、(P = (0,0)\) と(Q = (a,b)RNN) の特殊例である。
For a vector \(\textbf{v} = (a,b)\) in \(\mathbb{R}^{2}), the magnitude of \(\textbf{v}) is the magnitude is in:
また, ベクトルの大きさを計算するには, ユークリッド空間における点の距離の公式が必要です(証明は次節で):
Theorem 1.If.If.If.If.If.If.If.If.If.If.If.If.If.If.If.(If.If.)。1
Ⓐの点﹑(P = (x_{1}, y_{1}, z_{1})Ⓐと﹑(Q = (x_{2}, y_{2}, z_{2})Ⓖの間の距離⒜は次式となる。
この証明には次の結果を用います:
Theorem 1.2
For a vector \(\textbf{v} = (a,b,c)\) in \(\mathbb{R}^{3}), the magnitude of \(\textbf{v}) is:
PROof: 4つの場合を考えます。
\(a = b = c = 0) Then \(\textbf{v} = \textbf{0}}), so \(\norm{Cachetextbf{v}} = 0 = \sqrt{0^{2}}). + 0^{2} + 0^{2}} = \sqrt{a^{2}} となります。 + b^{2} + c^{2}}).
\(\textit{Case 2:}}) are \(a, b, c) are \(0}).
Encounter (Case2:}}は、Case2:}}の略です。 一般性を損なわない程度に、ここでは \(a = b = 0ờng) and \(c \ne 0ờng) とします(他の2つの可能性も同様に処理されます)。 そうすると、(0,0,c)の長さのベクトルである、(0,0,c)の長さのベクトルが(z軸)に沿って存在することになりま す。 ということで、♪ \norm{C} = | c | = \sqrt{c^{2}} = \sqrt{0^{2}} となります。 + 0^{2} + c^{2}} = \sqrt{a^{2}.. + b^{2} + c^{2}}).
\(\textit{Case 3:}) is \(a, b, c) is \(0}). 一般性を損なわない程度に、ここでは \(a = 0ờng), \(b \ne 0ờng), \(c \ne 0ờng) とします(他の2つの可能性も同様に処理します)。 そうすると、Ⓐtextbf{v} = (0,b,c)ⒷはⒶ平面上のベクトルなので、ピタゴラスの定理により、Ⓐnorm{Ⓐtextbf{v} =Ⓐsqrt{b^{2}Ⓐとなるのです。 + c^{2}} = \sqrt{0^{2}} となります。 + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}).
\(\textit{Case 4:}) \(\textit{none of })are \(a, b, c}) are 0}}. 一般性を損なわない範囲で、(他の7つの可能性も同様に)全て正であると仮定できます。 図1.1.8のように、点⇄(P = (0,0,0))⇄(Q = (a,b,c))⇄(R = (a,b,0),)⇄(S = (a,0,0))⇄で考える。 直角三角形にピタゴラスの定理を適用すると、ⒶⒷ= a^{2} + b^{2}Ⓑが得られます。 ピタゴラスの定理を直角三角形に適用すると、(PQR) = \norm{textbf{v}} = PQ \rightrvert = \sqrt{} PR \rightvert^{2} が得られます。 + \left}vert QR ↘↘↘= \sqrt{a^{2}. + b^{2} + c^{2}}\). これで定理が証明されました。
前( \tag{} (\textbf{QED})})
例題1.3
次のように計算しなさい:
- The magnitude of the vector (\overrightarrow{PQ}) in \(\mathbb{R}^{2}) with P = (-1,2)\ and \(Q = (5,5)\)in the \(㊦overrightarrow{PQ}).
⑭式(1.2)により、⑭(5-(-1))^{2}=⑯(PQ})⑯(P=(-1))^{2}になります。 + (5 – 2)^{2}} = \sqrt{36 + 9} = \sqrt{45} = 3 \sqrt{5}). - The magnitude of vector \(\textbf{v} = (8,3)\) in \(\mathbb{R}^{2}}).
- The magnitude of avector \(|sqrt{v}) = (8,3)¥Image.etc.
式(1.3)からは、(1.3)式で, \(\norm{Textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}).
- Ⓐの点Ⓐ(P = (2, -1, 4)Ⓑ)とⒷ(Q = (4, 2, -3)Ⓑ)との距離 (\textit{Solution:}) (1.4) 式より距離¥d = \sqrt{ (4 – 2)^{2} は¥1,000,000となり、②の点¥d = ¥1,000,000 となります。 + (2 – (-1))^{2} + (-3 – 4)^{2}} = \sqrt{4 + 9 + 49} = \sqrt{62}) となる。
- The magnitude of the vector \(\textbf{v} = (5,8,-2)\) in \(\mathbb{R}^{3}).
(\textit{Solution:}) By formula (1.5), \(\norm{THEBTF}} = \sqrt{5^{2}), \(\textbf{v}) = \sqrt{6}. + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}).
Contributors and Attributions
-
Michael Corral (Schoolcraft College)さん。 このページの内容はGNU Free Documentation License, Version 1.2の条項に従って配布されています。