11.1: Sistemi di coordinate tridimensionali
Nel calcolo a una variabile, le funzioni che si incontrano sono funzioni di una variabile (di solito \(x\) o \(t\)) che varia su qualche sottoinsieme della linea dei numeri reali (che indichiamo con \(\mathbb{R}). Per una tale funzione, per esempio, \(y = f(x)\), il \(\testobf{grafo}\) della funzione \(f\) consiste nei punti \((x, y) = (x, f(x))\). Questi punti giacciono nel ‗piano euclideo’, che, nel sistema di coordinate ‗cartesiano’ o ‗rettangolare’, consiste in tutte le coppie ordinate di numeri reali ‗(a, b)‖. Usiamo la parola “euclidea” per denotare un sistema in cui tutte le solite regole della geometria euclidea sono valide. Denotiamo il piano euclideo con \mathbb{R}^{2}}; il “2” rappresenta il numero di \dimensioni del piano. Il piano euclideo ha due assi perpendicolari: l’asse delle x e l’asse delle y.
Nel calcolo vettoriale (o multivariabile), ci occuperemo di funzioni di due o tre variabili (di solito rispettivamente \(x, y) o \(x, y, z)). Il grafico di una funzione di due variabili, per esempio, \(z = f(x,y)\), giace nello spazio euclideo, che nel sistema di coordinate cartesiane consiste di tutte le triple ordinate di numeri reali \(a, b, c)\). Poiché lo spazio euclideo è tridimensionale, lo indichiamo con \(\mathbb{R}^{3}}). Il grafico di \(f\) consiste nei punti \((x, y, z) = (x, y, f(x, y))\). Il sistema di coordinate tridimensionale dello spazio euclideo può essere rappresentato su una superficie piana, come questa pagina o una lavagna, solo dando l’illusione di tre dimensioni, nel modo mostrato nella figura 1.1.1. Lo spazio euclideo ha tre assi di coordinate mutuamente perpendicolari (\(x, y) e \(z)), e tre piani di coordinate mutuamente perpendicolari \piano!(figura 1.1.2).
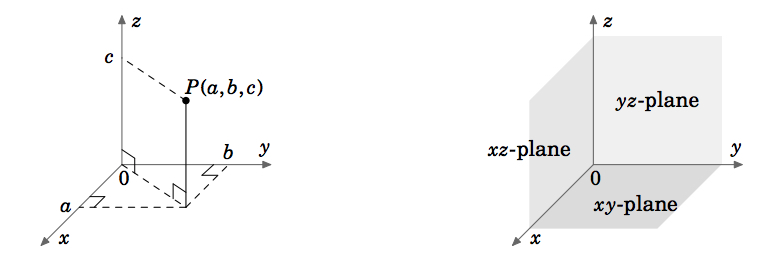
Il sistema di coordinate mostrato nella figura 1.1.Il sistema di coordinate mostrato nella figura 1.1.1 è conosciuto come un \sistema di coordinate per la mano destra, perché è possibile, usando la mano destra, puntare il dito indice nella direzione positiva dell’asse x, il dito medio nella direzione positiva dell’asse y, e il pollice nella direzione positiva dell’asse z, come nella figura 1.1.3.
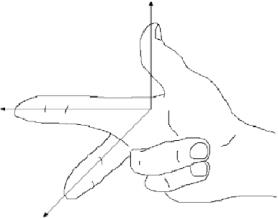
Fig 1.1.3: Sistema di coordinate destrorso.
Un modo equivalente di definire un sistema destrorso è se si può puntare il pollice verso l’alto nella direzione positiva dell’asse \(z)- mentre si usano le altre quattro dita per ruotare l’asse \(x)- verso l’asse \(y)-. Fare la stessa cosa con la mano sinistra è ciò che definisce un \testobf{sistema di coordinate per la mano sinistra}. Si noti che scambiando gli assi ⌦ x ⌫ e ⌦ y ⌫ in un sistema destrorso si ottiene un sistema sinistrorso, e che la rotazione di entrambi i tipi di sistema non cambia la sua “destrorsa”. Per tutto il libro useremo un sistema destrorso.
Per le funzioni di tre variabili, i grafici esistono nello spazio a 4 dimensioni (cioè \(\mathbb{R}^{4})), che non possiamo vedere nel nostro spazio tridimensionale, figuriamoci simulare nello spazio bidimensionale. Quindi possiamo pensare allo spazio a 4 dimensioni solo astrattamente. Per una discussione divertente su questo argomento, vedi il libro di ABBOT.
Finora abbiamo discusso il \testo di un oggetto nello spazio bidimensionale o tridimensionale. Ma che dire di qualcosa come la velocità dell’oggetto, o la sua accelerazione? O la forza gravitazionale che agisce sull’oggetto? Questi fenomeni sembrano tutti coinvolgere in qualche modo il movimento e la \direzione. È qui che entra in gioco l’idea di un \testo vettore\.
Hai già trattato la velocità e l’accelerazione nel calcolo a una variabile. Per esempio, per il moto lungo una linea retta, se \(y = f(t)\) dà lo spostamento di un oggetto dopo il tempo \(t\), allora \(dy/dt = f\,'(t)\) è la velocità dell’oggetto al tempo \(t\). La derivata \(f\(t)\) è solo un numero, che è positivo se l’oggetto si sta muovendo in una direzione “positiva” concordata, e negativo se si muove nella direzione opposta a quella direzione. Così si può pensare a quel numero, che è stato chiamato la velocità dell’oggetto, come avente due componenti: un \(\testo{magnitudine}\), indicato da un numero non negativo, preceduto da una direzione, indicata da un simbolo più o meno (che rappresenta il movimento nella direzione positiva o nella direzione negativa, rispettivamente), cioè \(f\(t) = \pm a\) per qualche numero \(a \ge 0\). Allora \(a\) è la grandezza della velocità (normalmente chiamata \textit{velocità}\ dell’oggetto), e il \(\pm\) rappresenta la direzione della velocità (anche se il \(+) è solitamente omesso per la direzione positiva).
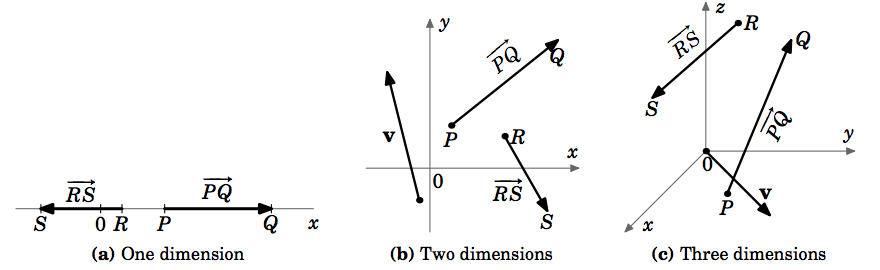
Per il moto lungo una linea retta, cioè in uno spazio 1-dimensionale, le velocità sono anche contenute in quello spazio 1-dimensionale, poiché sono solo numeri. Per il moto generale lungo una curva in uno spazio bidimensionale o tridimensionale, tuttavia, la velocità dovrà essere rappresentata da un oggetto multidimensionale che dovrebbe avere sia una grandezza che una direzione. Un oggetto geometrico che ha queste caratteristiche è una freccia, che nella geometria elementare è chiamata “segmento di linea diretta”. Questa è la motivazione di come definiremo un vettore.
Definizione 1.1
Un (non nullo) \testobf{vettore}} è un segmento di linea diretto tracciato da un punto \(P\) (detto il suo \testobf{ punto iniziale}) a un punto \(Q\) (detto il suo \testobf{ punto finale}), con \(P\) e \(Q\) punti distinti. Il vettore è indicato con \(\overrightarrow{PQ}). Il suo \testobf{magnitudo} è la lunghezza del segmento di retta, indicato con \norm{overrightarrow{PQ}}, e il suo \testobf{direzione}} è uguale a quello del segmento di retta diretto. Il ‗vettore zero’ è solo un punto, e viene indicato con ‖(‗testobf{0}).
Per indicare la direzione di un vettore, si traccia una freccia dal suo punto iniziale al suo punto terminale. Spesso indicheremo un vettore con una sola lettera in grassetto (ad esempio, \(\testobf{v})) e useremo i termini “magnitudine” e “lunghezza” in modo intercambiabile. Si noti che la nostra definizione potrebbe applicarsi a sistemi con qualsiasi numero di dimensioni (Figura 1.1.4 (a)-(c)).
Per quanto riguarda il vettore zero, bisogna notare alcune cose. La nostra motivazione su cosa sia un vettore includeva le nozioni di grandezza e direzione. Qual è la magnitudine del vettore zero? Definiamo che sia zero, cioè \(\norm{textbf{0}} = 0\). Questo concorda con la definizione del vettore zero come un semplice punto, che ha lunghezza zero. E la direzione del vettore zero? Un singolo punto non ha davvero una direzione ben definita. Notate che siamo stati attenti a definire solo la direzione di un vettore \(\textit{nonzero}), che è ben definito poiché i punti iniziali e terminali sono distinti. Non tutti sono d’accordo sulla direzione del vettore zero. Alcuni sostengono che il vettore zero ha una direzione (cioè può prendere qualsiasi direzione), alcuni dicono che ha una direzione (cioè la direzione non può essere determinata), mentre altri dicono che ha una direzione (cioè nessuna). La nostra definizione di vettore zero, tuttavia, non richiede che abbia una direzione, e la lasceremo così.
Ora che sappiamo cos’è un vettore, abbiamo bisogno di un modo per determinare quando due vettori sono uguali. Questo ci porta alla seguente definizione.
Definizione 1.2
Due vettori non nulli sono uguali se hanno la stessa grandezza e la stessa direzione. Qualsiasi vettore con magnitudine zero è uguale al vettore zero.
In base a questa definizione, vettori con la stessa magnitudine e direzione ma con punti iniziali diversi sarebbero uguali. Per esempio, nella figura 1.1.5 i vettori \(\testobf{u}), \(\testobf{v}) e \(\testobf{w}) hanno tutti la stessa grandezza \(\sqrt{5}) (per il Teorema di Pitagora). E vediamo che \(\testobf{u}) e \(\testobf{w}) sono paralleli, poiché giacciono su linee che hanno la stessa pendenza \frac{1}{2}, e puntano nella stessa direzione. Quindi \(\textbf{u} = \textbf{w}}), anche se hanno punti iniziali diversi. Vediamo anche che \(\textbf{v}) è parallelo a \(\textbf{u}) ma punta nella direzione opposta. Quindi \(\textbf{u} \ne \textbf{v})
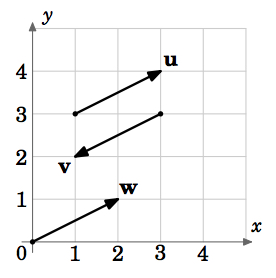
Così possiamo vedere che ci sono un numero infinito di vettori per una data grandezza e direzione, questi vettori sono tutti uguali e differiscono solo per i loro punti iniziali e finali. Esiste un unico vettore che possiamo scegliere per rappresentare tutti questi vettori uguali? La risposta è sì, ed è suggerita dal vettore \(\testobf{w}} nella figura 1.1.5.
Se non indicato diversamente, quando si parla di “il vettore” con una data grandezza e direzione, si intende quello il cui punto iniziale è nell’origine del sistema di coordinate.
Pensare ai vettori a partire dall’origine fornisce un modo di trattare i vettori in modo standard, poiché ogni sistema di coordinate ha un’origine. Ma ci saranno momenti in cui sarà conveniente considerare un punto iniziale diverso per un vettore (per esempio, quando si sommano i vettori, cosa che faremo nella prossima sezione). Un altro vantaggio di usare l’origine come punto iniziale è che fornisce una facile corrispondenza tra un vettore e il suo punto terminale.
Esempio 1.1
Sia \(\testobf{v}) il vettore in \(\mathbb{R}^{3}) il cui punto iniziale è nell’origine e il cui punto terminale è \(3,4,5)\. Anche se il \(\textit{point}) \((3,4,5)\ e il vettore \(\textbf{v}\ sono oggetti diversi, è conveniente scrivere \(\textbf{v} = (3,4,5)\). Facendo questo, si intende che il punto iniziale di \(\textbf{v}) è nell’origine \((0,0,0)\) e il punto terminale è \((3,4,5)\).
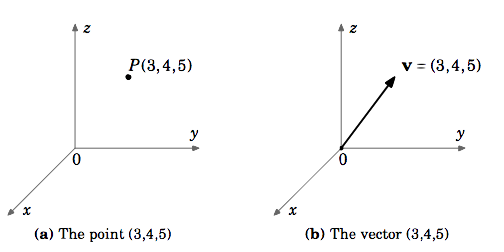
Salvo diversa indicazione, quando ci riferiamo ai vettori come \(\testobf{v} = (a,b)\) in \mathbb{R}^{2}} o \(\textbf{v} = (a,b,c)\) in \mathbb{R}^{3}), intendiamo vettori in coordinate cartesiane a partire dall’origine. Inoltre, scriveremo il vettore zero \(\textbf{0}}} in \(\mathbb{R}^{2}}) e \(\mathbb{R}^{3}}) come \((0,0)\) e \((0,0,0)\), rispettivamente.
La corrispondenza punto-vettore fornisce un modo semplice per verificare se due vettori sono uguali, senza dover determinare la loro grandezza e direzione. Simile a vedere se due punti sono uguali, ora stai vedendo se i punti terminali dei vettori che partono dall’origine sono uguali. Per ogni vettore, trova il vettore (unico!) che è uguale e il cui punto iniziale è l’origine. Poi confronta le coordinate dei punti terminali di questi “nuovi” vettori: se queste coordinate sono uguali, allora i vettori originali sono uguali. Per ottenere i “nuovi” vettori che partono dall’origine, si \textit{translate}\ ogni vettore per partire dall’origine sottraendo le coordinate del punto iniziale originale dal punto terminale originale. Il punto risultante sarà il punto terminale del “nuovo” vettore il cui punto iniziale è l’origine. Fate questo per ogni vettore originale poi confrontate.
Esempio 1.2
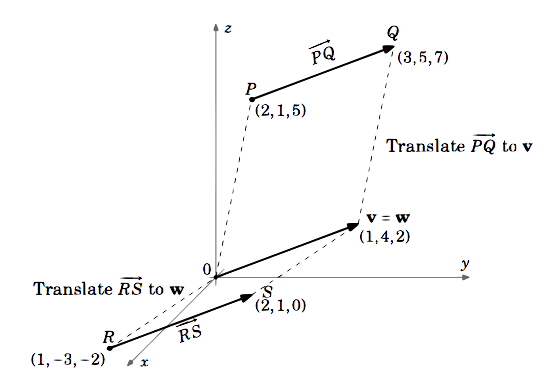
Considera i vettori \(\overrightarrow{PQ}}) e \(\overrightarrow{RS}}) in \(\mathbb{R}^{3}), dove \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\) e \(S = (2,1,0)\). Il \(\sopraccigliare{PQ} = \sopraccigliare{RS}}) è vero?
Il vettore \(\overrightarrow{PQ}) è uguale al vettore \(\textbf{v}) con punto iniziale \((0,0,0)\) e punto terminale \(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\).
Similmente, \(\overrightarrow{RS}}) è uguale al vettore \(\textbf{w}) con punto iniziale \((0,0,0)\) e punto terminale \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1, 1 – (-3),0 – (-2)) = (1,4,2)\).
Quindi \(\overrightarrow{PQ} = \textbf{v} = (1,4,2)\) e \(\overrightarrow{RS} = \textbf{w} = (1,4,2)\).
(quindi \sopra la freccia destra{PQ} = \sopra la freccia destra{RS})
Ricorda la formula della distanza per i punti nel piano euclideo:
Per i punti \(P = (x_{1}, y_{1})\), \(Q = (x_{2}, y_{2})\) in \(\mathbb{R}^{2}), la distanza \(d\) tra \(P\) e \(Q\) è:
Con questa formula, abbiamo il seguente risultato:
Nota
Per un vettore \(\overrightarrow{PQ}) in \(\mathbb{R}^{2}) con punto iniziale \(P = (x_{1}, y_{1})\) e punto terminale \(Q = (x_{2}, y_{2})\), la grandezza di \(\overrightarrow{PQ}) è:
Trovare la grandezza di un vettore \(\testobf{v} = (a,b)\) in \(\mathbb{R}^{2}}) è un caso speciale della formula precedente con \(P = (0,0)\) e \(Q = (a,b)\):
Per un vettore \(\textbf{v} = (a,b)\) in \(\mathbb{R}^{2}), la grandezza di \(\textbf{v}) è:
Per calcolare la grandezza dei vettori in \(\mathbb{R}^{3}}), abbiamo bisogno di una formula di distanza per punti nello spazio euclideo (rimandiamo la dimostrazione alla prossima sezione):
Teorema 1.1
La distanza \(d\) tra i punti \(P = (x_{1}, y_{1}, z_{1})\) e \(Q = (x_{2}, y_{2}, z_{2})\) in \(\mathbb{R}^{3}) è:
La dimostrazione utilizzerà il seguente risultato:
Teorema 1.2
Per un vettore \(\testobf{v} = (a,b,c)\) in \(\mathbb{R}^{3}), la grandezza di \(\testobf{v}) è:
Prova: Ci sono quattro casi da considerare:
(\textit{Caso 1:}) \(a = b = c = 0\). Allora \(\testobf{v} = \testobf{0}}), quindi \(\norm{{testobf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2} = \sqrt{a^{2} + b^{2} + c^{2}}).
(\textit{Caso 2:}) \(\textit{esattamente due di })\(a, b, c) sono \(0\). Senza perdita di generalità, assumiamo che \(a = b = 0\) e \(c \ne 0\) (le altre due possibilità sono gestite in modo simile). Allora \(\testobf{v} = (0,0,c)\), che è un vettore di lunghezza \(|c|) lungo l’asse \(z)-. Quindi \norm(\testobf{v} = | c | = \sqrt{c^{2}} = \sqrt{0^{2} + 0^{2} + c^{2} = \sqrt{a^{2} + b^{2} + c^{2}}).
(\textit{Caso 3:}) \(\textit{ esattamente uno di })\(a, b, c) è \(0\). Senza perdita di generalità, assumiamo che \(a = 0\), \(b \ne 0\) e \(c \ne 0\) (le altre due possibilità sono gestite in modo simile). Allora \(\textbf{v} = (0,b,c)\), che è un vettore nel \(yz)-piano, quindi per il Teorema di Pitagora abbiamo \(\norm{{{bf{v}} = \sqrt{b^{2} + c^{2} = \sqrt{0^{2} + b^{2} + c^{2} = \sqrt{a^{2} + b^{2} + c^{2}}).
(\textit{Caso 4:}) \(\textit{nessuno di })\(a, b, c) sono \(0\). Senza perdita di generalità, possiamo assumere che \(a, b, c) siano tutti positivi (le altre sette possibilità sono gestite in modo simile). Consideriamo i punti \(P = (0,0,0)\), \(Q = (a,b,c)\), \(R =(a,b,0),\) e \(S = (a,0,0)\), come mostrato in figura 1.1.8. Applicando il Teorema di Pitagora al triangolo rettangolo \(\triangolo PSR\) si ottiene \(\left\vert PR \right\vert^{2} = a^{2} + b^{2}). Una seconda applicazione del Teorema di Pitagora, questa volta al triangolo rettangolo (triangolo PQR), dà \normalità del testo bf{v} = \left\lvert PQ \right\rvert = \sqrt{left\lvert PR \right\vert^{2} + \left\vert QR \right\vert^{2}} = \sqrt{ a^{2} + b^{2} + c^{2}}\). Questo dimostra il teorema.
(\tag(\testobf{QED})
Esempio 1.3
Calcolare quanto segue:
- La grandezza del vettore \(\overrightarrow{PQ}) in \(\mathbb{R}^{2}) con \(P = (-1,2)\) e \(Q = (5,5)\).
- La grandezza del vettore \(\textbf{v} = (8,3)\) in \(\mathbb{R}^{2}).
(\textit{Soluzione:}) Per la formula (1.3), \(\norm{{textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}).- La distanza tra i punti \(P = (2, -1, 4)\) e \(Q = (4, 2, -3)\) in \(\mathbb{R}^{2})
(\textit{Soluzione:}) Per la formula (1.4), la distanza \(d = \sqrt{(4 – 2)^{2} + (2 – (-1))^{2} + (-3 – 4)^{2}} = \sqrt{4 + 9 + 49} = \sqrt{62}\).- La grandezza del vettore \(\textbf{v} = (5,8,-2)\) in \(\mathbb{R}^{3})
(\textit{Soluzione:}) Per la formula (1.5), \(\norm{\textbf{v}} = \sqrt{5^{2} + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}\). - La grandezza del vettore \(\textbf{v} = (8,3)\) in \(\mathbb{R}^{2}).
Contribuenti e attribuzioni
-
Michael Corral (Schoolcraft College). Il contenuto di questa pagina è distribuito sotto i termini della GNU Free Documentation License, versione 1.2.