Kahdeksankymmenennen vuosisadan alussa Göttingenin yliopisto oli yksi maailman parhaista matematiikan tutkimuskeskuksista. Matemaatikko David Hilbert oli siellä vakiintunut professori, ja talvilukukaudella 1924-25 hän piti sarjan luentoja äärettömyydestä matematiikassa, fysiikassa ja tähtitieteessä. (Nämä ja muut Hilbertin luennot on nyt julkaissut kirjana Springer-Verlag. Kirja on saatavana IAS:n kirjastosta suomennettuna ja saksankielisenä alkuperäiskappaleena). Eräässä näistä luennoista hän käytti esimerkkiä selittääkseen äärellisten ja äärettömien joukkojen välisen ratkaisevan eron: hotellissa, jossa on äärellinen määrä huoneita, jos kaikki huoneet on varattu, ei ole tilaa uusille vieraille. Mutta hotellissa, jossa on äärettömän monta huonetta, tämä ei ole ongelma: jos kaikki huoneet ovat varattuja ja uusi vieras saapuu, jokainen vanha vieras siirretään yksinkertaisesti yhden huoneen verran eteenpäin, jolloin ensimmäinen huone jää vapaaksi uutta vierasta varten. Samanlaisen argumentin avulla voimme majoittaa minkä tahansa äärellisen määrän ja jopa äärettömän monta uutta vierasta.

George Gamow (joka on kirjoittanut kuuluisan Alpher-Bethe-Gamow-paperin fysikaalisen kosmologian alalla) oli kesällä postdoc Göttingenin yliopistossa muutama vuosi näiden luentojen jälkeen ja luultavasti oppi Hilbertin esimerkin äärettömästä hotellista siellä. Hän popularisoi sitä vuonna 1947 ilmestyneessä populaaritieteellisessä kirjassaan One Two Three… Infinity: Facts and Speculations of Science (saatavilla Princetonin yliopiston kirjastosta).

Palataanpa vielä Hilbertin hotelliin. Siisteyden vuoksi sanotaan, että hotellin äärettömän monet huoneet on numeroitu 1, 2, 3, 4, 5, … . Eräänä yönä kaikki huoneet ovat varattuja, mutta paikalle saapuu uusi vieras. Kuten sanoimme aiemmin, siirretään huoneessa 1 oleva vieras huoneeseen 2, huoneessa 2 oleva vieras huoneeseen 3, huoneessa 3 oleva vieras huoneeseen 4 ja yleensä huoneessa n oleva vieras huoneeseen n + 1. Näin huoneeseen 1 vapautuu tilaa uudelle vieraalle, mutta kukaan alkuperäisistä vieraista ei jää kodittomaksi.

Nyt sanotaan, että paikalle saapuu kaksikymmentä uutta vierasta yhden sijaan. Aiemmin käytetty temppu toimii yhtä hyvin: siirretään huoneessa 1 oleva vieras huoneeseen 21, huoneessa 2 oleva vieras huoneeseen 22 ja yleensä huoneessa n oleva vieras huoneeseen n+20. Näin jää kaksikymmentä huonetta vapaaksi ja valmiiksi kahdellekymmenelle uudelle vieraalle.

Mutta entä jos äärettömän monta uutta vierasta saapuu äärettömän bussin kyydissä? Voimme muuttaa edellistä väitettä niin, että se toimii edelleen tässä tilanteessa: sijoita hotellissa jo olevat vieraat niin, että he miehittävät vain joka toisen huoneen. Matemaattisesti sanottuna siirretään huoneessa n oleva vieras huoneeseen 2n niin, että kaikki parilliset huoneet ovat varattuja. Näin kaikki muut huoneet (äärettömän monta!) jäävät tyhjiksi ja ovat valmiina majoittamaan bussilla saapuvat (äärettömän monta!) ihmistä. Henkilön, joka istuu bussissa paikassa numero n, pitäisi siirtyä n:nteen parittomaan huoneeseen, joka on huone numero 2n – 1.

Entä jos saapuu yhdeksänkymmentäyhdeksän ääretöntä bussia? Siirretään yksinkertaisesti alkuperäiset hotellivieraat huoneisiin 100, 200, 300 jne., ensimmäisen bussin matkustajat huoneisiin 1, 101, 201 jne., toisen bussin matkustajat huoneisiin 2, 102, 202 jne. ja niin edelleen loput bussit. Näin saadaan kaikki hotellin huoneet täyteen, mutta yksikään vieras ei jää ilman huonetta. Jos bussimatkustajat olisivat itse numeroituja 1, 2, 3, 4, 5, . . . (emmekä tee eroa ja kutsumme myös hotellin alkuperäisiä vieraita matkustajiksi – voimme ajatella, että kaikki alkuperäiset vieraat siirretään pois hotellista suoraan hotellin ulkopuolelle pysäköityyn koristeelliseen linja-autoon, jota voimme kutsua linja-autoksi numero 0), hotellin ensimmäiset sata huonetta täytetään matkustajilla numero 1, hotellin toiset sata huonetta täytetään matkustajilla numero 2 ja niin edelleen.

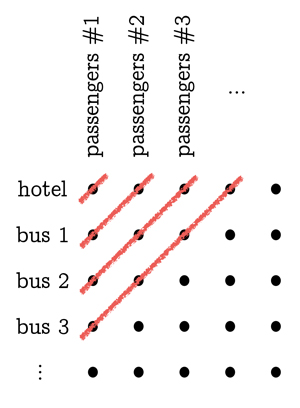
Seuraavalla tasolla käsitellään äärettömän monta ääretöntä bussia (jokaisessa bussissa äärettömän monta matkustajaa). Ensimmäiseksi kaikki on saatava ulos hotellista ja busseista ja järjestäytymään ruudukkomaisesti parkkipaikalle tai paperille: laita hotellin alkuperäiset vieraat (eli bussin 0 matkustajat) riviin järjestyksessä vasemmalta oikealle muodostaen rivin. Pyydä ensimmäisen bussin matkustajia muodostamaan toinen rivi heti ensimmäisen bussin alapuolelle ja toisen bussin matkustajia toisen bussin alapuolelle jne. Järjestä rivit toisiinsa siten, että kunkin bussin matkustajat numero 1 asettuvat sarakkeeseen, matkustajat numero 2 kyseisen bussin oikealla puolella olevaan sarakkeeseen ja niin edelleen. Jos nyt alamme täyttää hotellihuoneita 1, 2, 3, 4, . . . ensimmäiseltä riviltä tulevilla ihmisillä, emme saa sitä koskaan valmiiksi ja siirrymme toiselle riville, ja samoin käy, jos yritämme aloittaa ensimmäisestä sarakkeesta. Temppu on ajatella diagonaalisia viivoja, jotka kulkevat ruudukossa alhaalta vasemmalta ylhäältä oikealle. Vasemmanpuoleisin näistä diagonaaliviivoista osuu vain yhteen ylävasemmalla olevaan henkilöön (bussi 0, matkustaja 1): laita tämä henkilö huoneeseen 1. Seuraava diagonaaliviiva osuu kahteen henkilöön (bussi 1, matkustaja 1 ja bussi 0, matkustaja 2): laita nämä kaksi henkilöä huoneisiin 2 ja 3. Seuraava diagonaaliviiva osuu kolmeen henkilöön: laita heidät kolmeen seuraavaan tyhjään huoneeseen 4, 5 ja 6. Jatkamalla tätä kaavaa osoitamme lopulta huoneen jokaiselle parkkipaikalla kärsivällisesti seisovalle ihmiselle.

Voidaanko mennä syvemmälle äärettömyyteen, syvemmälle kuin äärettömän monta ääretöntä bussia? Kyllä voimme: kuvitellaan, että aivan Hilbertin hotellin vieressä on parkkihalli. Ensimmäisessä kerroksessa, aivan hotellin oven vieressä, on jo tuntemamme äärettömän monta ääretöntä bussia. Mutta sitten huomaamme: parkkihallissa on äärettömän monta kerrosta, joissa jokaisessa on äärettömän monta ääretöntä bussia. Pystyykö Hilbertin hotelli selviytymään tästä lisätystä äärettömyyden kerroksesta? Vastaus on kyllä! Voit kuvitella käyttäväsi edellistä menetelmää tehdäksesi yhden matkustajaryhmän parkkihallin jokaiseen kerrokseen ja käskeä sitten jokaisen matkustajaryhmän mennä yhteen äärettömään bussiin. Nyt olemme pienentäneet ongelman takaisin äärettömän moneen äärettömään bussiin, joiden tiedämme mahtuvan hotelliin.

Entä jos lisäämme toisen äärettömyyskerroksen? Jos esimerkiksi on äärettömän monta parkkihallia, joissa jokaisessa on äärettömän monta kerrosta, jokaisessa kerroksessa äärettömän monta bussia, jokaisessa bussissa äärettömän monta matkustajaa? Se on neljä äärettömyyden kerrosta, ja vastaus on edelleen kyllä! Itse asiassa vastaus on kyllä jopa neljälle tuhannelle äärettömyyden kerrokselle. Loppuuko se koskaan? Eikö Hilbertin hotelli koskaan pysty ottamaan uusia vieraita? Onko olemassa ääretöntä, joka on liian suuri Hilbertin hotellille?

Kyllä on. Todellakin, jos meillä olisi äärettömän monta äärettömyyskerrosta, kaikkia näitä ihmisiä ei mitenkään voisi majoittaa Hilbertin hotelliin. Joten …mitä tapahtuu? Osoittautuu, että kaikki kuvatut äärettömyydet tähän viimeiseen asti ovat samankokoisia. Tätä kokoa kutsutaan nimellä ℵ0 (alef nolla), joka on joukon ℕ = {1, 2, 3, 4, …} koko ja se, kuinka monta huonetta Hilbertin hotellissa on. Georg Cantor esitti vuonna 1874 ajatuksen siitä, miten äärettömyyksien kokoja voidaan vertailla, ja osoitti, että on olemassa erikokoisia äärettömyyksiä. Useat merkittävät matemaatikot (Poincaré, Kronecker ja myöhemmin Weyl) vastustivat jyrkästi hänen ajatuksiaan, samoin kuin jotkut teologit – nämä väittivät, että Cantorin ajatukset kyseenalaistivat Jumalan absoluuttisen äärettömyyden ainutkertaisuuden. Hilbert sen sijaan tuki ja puolusti Cantoria.

Äärettömien joukkojen koon vertailu ei eroa kovin paljon äärellisten joukkojen koon vertailusta: jos haluaa tietää, onko luentosalissa enemmän tuoleja vai enemmän ihmisiä, ei tarvitse laskea ihmisiä ja tuoleja ja verrata näitä kahta lukua. Voit vain vilkaista huonetta ja katsoa, onko siellä tyhjiä tuoleja (enemmän tuoleja kuin ihmisiä) tai seisovia ihmisiä (enemmän ihmisiä kuin tuoleja): jos jokainen ihminen istuu tuolissa eikä tyhjiä tuoleja ole, tuolijoukko ja ihmisjoukko ovat samankokoisia. Vastaavasti, jos jokaiselle bussimatkustajalle osoitetaan huone Hilbertin hotellissa eikä yhtään huonetta jätetä tyhjäksi, niin matkustajien joukko on ääretön ja samankokoinen kuin Hilbertin hotellin huoneiden joukko, ℵ0. Cantor käytti tätä ajatusta osoittaakseen, että reaalilukujen joukko ℝ on tiukasti suurempi kuin luonnollisten lukujen joukko ℕ; hänen kaunis argumenttinsa tuli tunnetuksi nimellä ”Cantorin diagonaali”. Cantor myös arveli – ja yritti todistaa, mutta epäonnistui – jatkumohypoteesin: ei ole olemassa ääretöntä joukkoa, joka olisi tiukasti suurempi kuin ℕ mutta tiukasti pienempi kuin ℝ. Hilbert sisällytti väitteen paikkansapitävyyden todistamisen ensimmäiseksi ongelmaksi kuuluisaan kahdenkymmenenkolmen ongelman luetteloon, jonka hän esitti vuonna 1900 Pariisissa pidetyssä kansainvälisessä matemaatikkojen kongressissa ja joka muokkasi matematiikan tutkimuksen suuntaa vuosikymmeniksi eteenpäin. Vastaus on, että tätä hypoteesia ei voida todistaa vääräksi (Gödel, 1940-luku), mutta sitä ei myöskään voida todistaa todeksi (Cohen, 1960-luku): se on ratkaisematon ongelma!

Hilbert sanoi tunnetusti Cantorin ajatuksista äärettömyydestä ja kaikesta siitä uudesta matematiikasta, jonka ne toivat mukanaan: ”Kukaan ei saa karkottaa meitä paratiisista, jonka Cantor on luonut.”