11.1: Trójwymiarowe układy współrzędnych
W rachunku jednej zmiennej, funkcje, z którymi się spotykamy, są funkcjami zmiennej (zwykle x lub t), która zmienia się na pewnym podzbiorze linii liczb rzeczywistych (który oznaczamy przez \(\mathbb{R}}). Dla takiej funkcji, powiedzmy, \(y = f(x)\), \(\textbf{graph}\) funkcji \(f\) składa się z punktów \((x, y) = (x, f(x))\). Punkty te leżą na płaszczyźnie euklidesowej, która w układzie współrzędnych kartezjańskich lub prostokątnych składa się ze wszystkich uporządkowanych par liczb rzeczywistych \((a, b)\). Używamy słowa „Euklidesowy” na oznaczenie układu, w którym obowiązują wszystkie zwykłe zasady geometrii euklidesowej. Płaszczyznę euklidesową oznaczamy przez \(\mathbb{R}^{2}\); „2” oznacza liczbę \(\textit{dimensions}\) płaszczyzny. Płaszczyzna euklidesowa ma dwie prostopadłe osie współrzędnych: oś x i oś y. W rachunku wektorowym (lub wielozmiennowym) będziemy zajmować się funkcjami dwóch lub trzech zmiennych (zwykle odpowiednio x, y lub x, y, z). Wykres funkcji dwóch zmiennych, powiedzmy \(z = f(x,y)\), leży w przestrzeni euklidesowej, która w kartezjańskim układzie współrzędnych składa się ze wszystkich uporządkowanych trójek liczb rzeczywistych \((a, b, c)\). Ponieważ przestrzeń euklidesowa jest trójwymiarowa, oznaczamy ją przez \(\mathbb{R}^{3}\). Graf ˆ(f) składa się z punktów ˆ((x, y, z) = (x, y, f(x, y))ˆ). Trójwymiarowy układ współrzędnych przestrzeni euklidesowej może być przedstawiony na płaskiej powierzchni, takiej jak ta strona lub tablica, tylko poprzez stworzenie iluzji trzech wymiarów, w sposób pokazany na rysunku 1.1.1. Przestrzeń euklidesowa ma trzy wzajemnie prostopadłe osie współrzędnych (x, y i z) oraz trzy wzajemnie prostopadłe płaszczyzny współrzędnych: współrzędną \(x, y) i \(z).(rysunek 1.1.2).
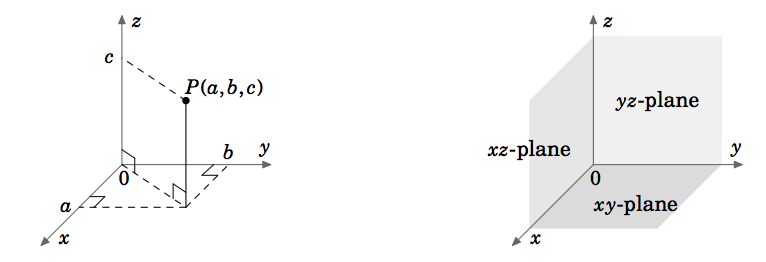
Układ współrzędnych pokazany na rysunku 1.1.1 jest znany jako \tekstbf{prawostronny układ współrzędnych}, ponieważ możliwe jest, przy użyciu prawej ręki, skierowanie palca wskazującego w dodatnim kierunku osi \ (x), palca środkowego w dodatnim kierunku osi \ (y), a kciuka w dodatnim kierunku osi \ (z), jak na rysunku 1.1.3.
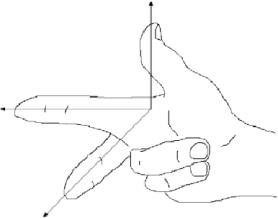
Rys. 1.1.3: Prawostronny układ współrzędnych.
Równoważnym sposobem zdefiniowania układu prawostronnego jest sytuacja, w której można skierować kciuk do góry w kierunku dodatniej osi \(z), jednocześnie używając pozostałych czterech palców do obracania osi \(x) w kierunku osi \(y). Wykonanie tej samej czynności lewą ręką jest tym, co definiuje \(\textbf{lewostronny układ współrzędnych}). Zauważmy, że zamiana osi x i y w układzie prawostronnym daje w rezultacie układ lewostronny, a obracanie któregokolwiek z tych układów nie zmienia jego „ręczności”. W całej książce będziemy używać układu prawostronnego.
Dla funkcji trzech zmiennych wykresy istnieją w przestrzeni czterowymiarowej (tzn. \(\matb{R}^{4}}), której nie możemy zobaczyć w naszej przestrzeni trójwymiarowej, a tym bardziej symulować w przestrzeni dwuwymiarowej. Tak więc o przestrzeni 4-wymiarowej możemy myśleć tylko abstrakcyjnie. Zabawną dyskusję na ten temat można znaleźć w książce ABBOT.
Do tej pory omówiliśmy położenie obiektu w przestrzeni dwuwymiarowej lub trójwymiarowej. Ale co z czymś takim jak prędkość obiektu, czy jego przyspieszenie? Albo siła grawitacji działająca na obiekt? Wydaje się, że wszystkie te zjawiska w jakiś sposób wiążą się z ruchem i kierunkiem. W tym miejscu pojawia się idea wektora.
Miałeś już do czynienia z prędkością i przyspieszeniem w rachunku jednej zmiennej. Na przykład, dla ruchu wzdłuż linii prostej, jeśli \(y = f(t)\) daje przemieszczenie obiektu po czasie \(t)\), to \(dy/dt = f\,'(t)\) jest prędkością obiektu w czasie \(t)\). Pochodna \(f\,'(t)\) to po prostu liczba, która jest dodatnia, jeśli obiekt porusza się w uzgodnionym „dodatnim” kierunku, i ujemna, jeśli porusza się w kierunku przeciwnym do tego kierunku. Można więc myśleć o tej liczbie, którą nazywano prędkością obiektu, jako o liczbie składającej się z dwóch elementów: a, oznaczonej liczbą nieujemną, poprzedzonej kierunkiem, oznaczonym symbolem plusa lub minusa (oznaczającym odpowiednio ruch w kierunku dodatnim lub ujemnym), tzn. \(f\,'(t) = \pm a\) dla pewnej liczby \(a \ge 0\). Wtedy \(a \) jest wielkością prędkości (zwykle nazywaną \tekstem prędkości obiektu), a \(\pm \) reprezentuje kierunek prędkości (chociaż \(+ \) jest zwykle pomijany dla kierunku dodatniego).
Dla ruchu wzdłuż linii prostej, tj. w przestrzeni jednowymiarowej, prędkości są również zawarte w tej jednowymiarowej przestrzeni, ponieważ są tylko liczbami. Jednak dla ogólnego ruchu wzdłuż krzywej w przestrzeni dwu- lub trójwymiarowej, prędkość będzie musiała być reprezentowana przez obiekt wielowymiarowy, który powinien mieć zarówno wielkość jak i kierunek. Obiektem geometrycznym, który posiada te cechy jest strzałka, która w geometrii elementarnej nazywana jest „odcinkiem prostej skierowanej”. To jest motywacja do tego, jak będziemy definiować wektor.
Definicja 1.1
Wektor (niezerowy) to skierowany odcinek linii poprowadzony od punktu P (zwanego jego punktem początkowym) do punktu Q (zwanego jego punktem końcowym), przy czym punkty P i Q są różne. Wektor jest oznaczany przez \(\overrightarrow{PQ}}). Jego długość jest równa długości odcinka, oznaczonego jako \norma \overrightarrow{PQ}}, a jego \tekstbf{direction}} jest taki sam jak odcinka skierowanego. Wektor zerowy jest tylko punktem i jest oznaczany przez \(\textbf{0}}).
Aby wskazać kierunek wektora, rysujemy strzałkę od jego punktu początkowego do punktu końcowego. Zauważmy, że nasza definicja może mieć zastosowanie do układów o dowolnej liczbie wymiarów (Rysunek 1.1.4 (a)-(c)).
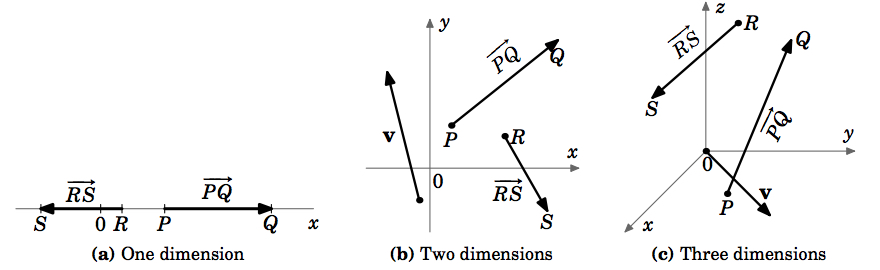
Należy zwrócić uwagę na kilka rzeczy dotyczących wektora zerowego. Nasze uzasadnienie tego, czym jest wektor, zawierało pojęcia wielkości i kierunku. Jaka jest wielkość wektora zerowego? Zdefiniujemy ją jako zerową, tzn. Zgadza się to z definicją wektora zerowego jako po prostu punktu, który ma zerową długość. A co z kierunkiem wektora zerowego? Pojedynczy punkt tak naprawdę nie ma dobrze zdefiniowanego kierunku. Zauważ, że byliśmy ostrożni, aby zdefiniować tylko kierunek wektora zerowego, który jest dobrze zdefiniowany, ponieważ punkty początkowy i końcowy są różne. Nie wszyscy zgadzają się co do kierunku wektora zerowego. Niektórzy twierdzą, że wektor zerowy ma kierunek ∗ (tzn. może mieć dowolny kierunek), inni, że ma kierunek ∗ (tzn. kierunek nie może być określony), a jeszcze inni, że ma kierunek ∗ (brak kierunku). Nasza definicja wektora zerowego nie wymaga jednak, aby miał on kierunek i tak to zostawimy.
Teraz, gdy wiemy, czym jest wektor, potrzebujemy sposobu na określenie, kiedy dwa wektory są równe. To prowadzi nas do następującej definicji.
Definicja 1.2
Dwa niezerowe wektory są równe, jeśli mają tę samą wielkość i ten sam kierunek. Każdy wektor o zerowej wielkości jest równy wektorowi zerowemu.
Zgodnie z tą definicją wektory o tej samej wielkości i kierunku, ale o różnych punktach początkowych, byłyby równe. Na przykład na rysunku 1.1.5 wektory \(\textbf{u}), \(\textbf{v}) i \(\textbf{w}) mają tę samą wielkość \(\sqrt{5}) (zgodnie z twierdzeniem pitagorejskim). Widzimy też, że \tekstbf{u} \ i \tekstbf{w} \ są równoległe, ponieważ leżą na prostych o tym samym nachyleniu \ i są skierowane w tym samym kierunku. Zatem \(\textbf{u} = \textbf{w}), mimo że mają różne punkty początkowe. Widzimy również, że \(\textbf{v}}) jest równoległa do \(\textbf{u}}, ale wskazuje w przeciwnym kierunku. Widzimy więc, że istnieje nieskończona liczba wektorów dla danej wielkości i kierunku, przy czym wszystkie te wektory są równe i różnią się tylko punktami początkowymi i końcowymi. Czy istnieje pojedynczy wektor, który możemy wybrać do reprezentowania wszystkich tych równych wektorów? Odpowiedź jest twierdząca, a sugeruje ją wektor \(\) na rysunku 1.1.5.
Jeśli nie zaznaczono inaczej, mówiąc o „wektorze” o danej wielkości i kierunku, będziemy mieli na myśli ten, którego punkt początkowy znajduje się w początku układu współrzędnych.
Myślenie o wektorach jako zaczynających się od początku zapewnia sposób radzenia sobie z wektorami w standardowy sposób, ponieważ każdy układ współrzędnych ma początek. Ale będą sytuacje, w których wygodnie będzie rozważyć inny punkt początkowy dla wektora (na przykład podczas dodawania wektorów, co zrobimy w następnym rozdziale). Inną zaletą używania początku jako punktu początkowego jest to, że zapewnia to łatwą zgodność między wektorem a jego punktem końcowym.
Przykład 1.1
Niech \(\textbf{v}\) będzie wektorem w \(\mathbb{R}^{3}\), którego punkt początkowy jest w początku i którego punktem końcowym jest \((3,4,5)\). Chociaż punkt początkowy \(3,4,5)\) i wektor \(\textbf{v}} są różnymi obiektami, wygodnie jest pisać \(\textbf{v} = (3,4,5)\). Rozumie się przy tym, że punkt początkowy ˆ(ˆtextbf{v}}) znajduje się na początku ˆ((0,0,0)ˆ), a punkt końcowy ˆ((3,4,5)ˆ).
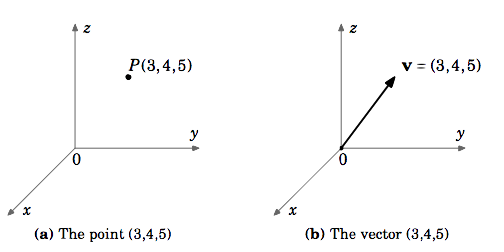
Jeśli nie zaznaczono inaczej, to gdy mówimy o wektorach jako o \(\tekstbf{v} = (a,b)\) w \(\mathbb{R}^{2}) lub \(\textbf{v} = (a,b,c)\) w \(\mathbb{R}^{3}), mamy na myśli wektory we współrzędnych kartezjańskich zaczynających się w punkcie początkowym. Również wektor zerowy \(\textbf{0}\) w \(\mathbb{R}^{{2}\) i \(\mathbb{R}^{3}\) będziemy zapisywać odpowiednio jako \((0,0)\) i \((0,0,0)\).
Korespondencja punkt-wektor zapewnia łatwy sposób sprawdzenia, czy dwa wektory są równe, bez konieczności określania ich wielkości i kierunku. Podobnie do sprawdzania, czy dwa punkty są takie same, teraz sprawdzasz, czy punkty końcowe wektorów zaczynających się w punkcie początkowym są takie same. Dla każdego wektora znajdź (jedyny!) równy mu wektor, którego punktem początkowym jest początek. Następnie porównaj współrzędne punktów końcowych tych „nowych” wektorów: jeśli te współrzędne są takie same, to oryginalne wektory są równe. Aby otrzymać „nowe” wektory zaczynające się w punkcie początkowym, odejmujemy współrzędne oryginalnego punktu początkowego od oryginalnego punktu końcowego każdego wektora. Otrzymany punkt będzie punktem końcowym „nowego” wektora, którego punktem początkowym jest początek. Zrób to dla każdego oryginalnego wektora, a następnie porównaj.
Przykład 1.2
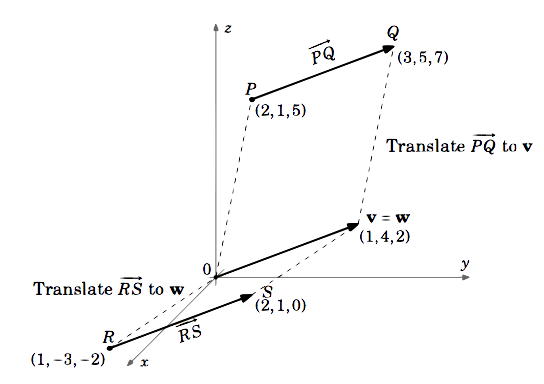
Rozważmy wektory \(\overrightarrow{PQ}} i \(\overrightarrow{RS}}} w \(\mathbb{R}^{3}}, gdzie \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\) i \(S = (2,1,0)\).
Wektor \(\overrightarrow{PQ}) jest równy wektorowi \(\textbf{v}) z punktem początkowym \((0,0,0)\) i punktem końcowym \(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\).
(itherefore \overrightarrow{PQ} = \overrightarrow{RS})
Przypomnij sobie wzór na odległość dla punktów na płaszczyźnie euklidesowej:
Dla punktów \(P = (x_{1}, y_{1})\), \(Q = (x_{2}, y_{2})\) na płaszczyźnie euklidesowej, odległość \(d) między \(P\) i \(Q\) wynosi:
Z tego wzoru otrzymujemy następujący wynik:
Uwaga
Dla wektora \(\overrightarrow{PQ}\) w \(\mathbb{R}^{2}\) z punktem początkowym \(P = (x_{1}, y_{1})\) i punktem końcowym \(Q = (x_{2}, y_{2})\), wielkość \(\overrightarrow{PQ}}) wynosi:
Znalezienie wielkości wektora \(\textbf{v} = (a,b)\) w \(\mathbb{R}^{2}\) jest szczególnym przypadkiem powyższego wzoru z \(P = (0,0)\) i \(Q = (a,b)\):
Dla wektora \(\textbf{v} = (a,b)\) w \(\mathbb{R}^{2}\), wielkość \(\textbf{v}) wynosi:
Aby obliczyć wielkość wektorów w
potrzebujemy wzoru na odległość dla punktów w przestrzeni euklidesowej (dowód odłożymy do następnego rozdziału):
Twierdzenie 1.1
Dystans d między punktami \(P = (x_{1}, y_{1}, z_{1})\) i \(Q = (x_{2}, y_{2}, z_{2})\) w \(\) wynosi:
Dowód będzie korzystał z następującego wyniku:
Twierdzenie 1.2
Dla wektora \(\textbf{v} = (a,b,c)\) w \(\mathbb{R}^{3}}, wielkość \(\textbf{v}) wynosi:
Dowód: Wtedy \(\textbf{v} = \textbf{0}), więc \(\norma{textbf{v}} = 0 = \sqrt{0^{2} + 0^{2} + 0^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}).
\(\tekstit{przypadek 2:\) \(\tekstit{dokładnie dwa z \)\(a, b, c\) są \(0). Bez straty ogólności zakładamy, że \(a = b = 0\) i \(c = 0\) (pozostałe dwie możliwości są traktowane w podobny sposób). Wtedy \(\textbf{v} = (0,0,c)\), czyli wektor o długości \(|c|) wzdłuż osi \(z\). Zatem \norma{textbf{v}} = | c | = \sqrt{c^{2}} = \sqrt{0^{2} + 0^{2} + c^{2}} = \sqrt{a^{2} + c^{2}} = \sqrt{0^{2} + b^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}).
\(\tekstit{przypadek 3:\) \(\tekstit{dokładnie jeden z \) \(a, b, c\) jest \(0\). Bez straty ogólności zakładamy, że \(a = 0\), \(b = 0\) i \(c = 0\) (pozostałe dwie możliwości są traktowane w podobny sposób). Wtedy \(\textbf{v} = (0,b,c)\), który jest wektorem w płaszczyźnie \, więc przez Twierdzenie Pitagorejskie mamy \(\norma{textbf{v}} = \sqrt{b^{2} + c^{2}} = \sqrt{0^{2} + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}.
\(\tekstit{przypadek 4:\) \(\tekstit{żaden z \) \(a, b, c) są \(0\). Bez utraty ogólności możemy założyć, że wszystkie a, b, c są dodatnie (pozostałe siedem możliwości traktujemy w podobny sposób). Rozważmy punkty \(P = (0,0,0)\), \(Q = (a,b,c)\), \(R =(a,b,0),\) i \(S = (a,0,0)\), jak pokazano na rysunku 1.1.8. Zastosowanie twierdzenia pitagorejskiego do trójkąta prostokątnego PSR daje trójkąt PR ^{2} = a^{2} + b^{2}). Drugie zastosowanie twierdzenia pitagorejskiego, tym razem do trójkąta prostokątnego PQR daje \(\norma{textbf{v}} = \left \lvert PQ \right \rvert = \sqrt{ \left \vert PR \right \vert^{2} + \leftlvert QR \right\vert^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}\). To dowodzi twierdzenia.
(\tag{textbf{QED}})
Przykład 1.3
Oblicz, co następuje:
- Wielkość wektora \(\overrightarrow{PQ}}) w \(\mathbb{R}^{2}}) z \(P = (-1,2)\) i \(Q = (5,5)\).
- Wielkość wektora \(\textbf{v} = (8,3)\) w \(\mathbb{R}^{2}}.
Ze wzoru (1.3) wynika, że \(\norma{textbf{v}} = \sqrt{8^{2} + 3^{2}} = \sqrt{73}}).- Odległość między punktami \(P = (2, -1, 4)\) i \(Q = (4, 2, -3)\) w \(\mathbb{R}^{2}}.
Ze wzoru (1.4) wynika, że odległość \(d = \sqrt{(4 – 2)^{2} + (2 – (-1))^{2} + (-3 – 4)^{2}} = ^sqrt{4 + 9 + 49} = ^sqrt{62}).- Wielkość wektora \(\textbf{v} = (5,8,-2)\) w \(\mathbb{R}^{3}\).
Ze wzoru (1.5) wynika, że \(\norma{textbf{v}} = \sqrt{5^{2} + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}}). - Wielkość wektora \(\textbf{v} = (8,3)\) w \(\mathbb{R}^{2}}.
Współautorzy i przypisy
-
Michael Corral (Schoolcraft College). Zawartość tej strony jest rozpowszechniana na warunkach licencji GNU Free Documentation License, wersja 1.2.
.