11.1: Kolmiulotteiset koordinaatistot
Yksittäismuuttujalaskennassa kohtaamamme funktiot ovat sellaisen muuttujan (yleensä \(x\) tai \(t\)) funktioita, joka vaihtelee jossakin reaalilukusuoran osajoukossa (jota merkitsemme \(\mathbb{R}\)). Tällaisen funktion, esimerkiksi \(y = f(x)\), funktion \(f\) \(\textbf{graph}\) \(\textbf{graph}\) koostuu pisteistä \((x, y) = (x, f(x))\). Nämä pisteet sijaitsevat \(\textbf{Euklidinen taso}\), joka \(\textbf{Kartesilainen}\) tai \(\textbf{Suorakulmainen}\) koordinaatistossa koostuu kaikista järjestetyistä reaalilukupareista \((a, b)\). Käytämme sanaa ”euklidinen” tarkoittamaan järjestelmää, jossa kaikki tavanomaiset euklidisen geometrian säännöt pätevät. Merkitsemme euklidista tasoa \(\mathbb{R}^{2}\); ”2” tarkoittaa tason \(\textit{dimensions}\) lukumäärää. Euklidisella tasolla on kaksi kohtisuoraa \(\textbf{koordinaattiakselia}\): \(x\)-akseli ja \(y\)-akseli.
Vektorilaskennassa (tai monimuuttujalaskennassa) käsittelemme kahden tai kolmen muuttujan funktioita (yleensä \(x, y\) tai \(x, y, z\)). Kahden muuttujan funktion kuvaaja, esimerkiksi \(z = f(x,y)\), sijaitsee euklidisessa avaruudessa, joka kartesiolaisessa koordinaatistossa koostuu kaikista reaalilukujen järjestetyistä kolmioista \((a, b, c)\). Koska euklidinen avaruus on 3-ulotteinen, merkitsemme sitä \(\mathbb{R}^{3}\). Kuvaaja \(f\) koostuu pisteistä \((x, y, z) = (x, y, f(x, y))\). Euklidisen avaruuden kolmiulotteinen koordinaatisto voidaan esittää tasaisella pinnalla, kuten tällä sivulla tai taululla, vain antamalla illuusio kolmesta ulottuvuudesta kuvassa 1.1.1 esitetyllä tavalla. Euklidisessa avaruudessa on kolme toisiaan vastaan kohtisuorassa olevaa koordinaattiakselia (\(x, y\) ja \(z\)) ja kolme toisiaan vastaan kohtisuorassa olevaa koordinaattitasoa \indeksitaso!koordinaatti}: \(xy\)-taso, \(yz\)-taso ja \(xz\)-taso (kuva 1.1.2).
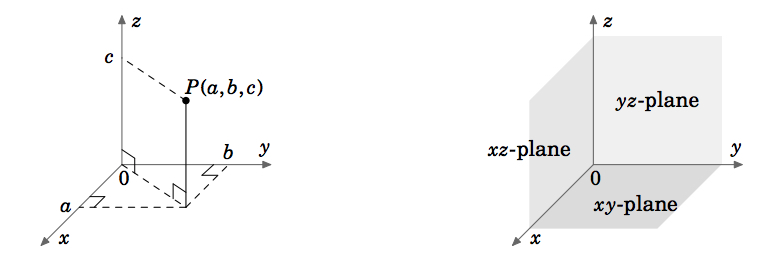
Kuvassa 1.1 esitetty koordinaatisto.1 tunnetaan \(\textbf{oikeakätinen koordinaatisto}\), koska oikealla kädellä on mahdollista osoittaa etusormi \(x\)-akselin positiiviseen suuntaan, keskisormi \(y\)-akselin positiiviseen suuntaan ja peukalo \(z\)-akselin positiiviseen suuntaan kuvan 1.1.1.1 mukaisesti.1.3.
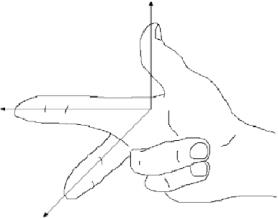
Kuva 1.1.3: Oikeakätinen koordinaatisto.
Yhtäläinen tapa määritellä oikeakätinen koordinaatisto on, jos pystyt osoittamaan peukalollasi ylöspäin positiiviseen \(z\)-akselin suuntaan samalla kun käytät jäljelle jääviä neljää sormea \(x\)-akselin pyörittämiseen \(y\)-akselia kohti. Saman asian tekeminen vasemmalla kädellä määrittelee \(\textbf{vasenkätinen koordinaatisto}\). Huomaa, että \(x\)- ja \(y\)-akselien vaihtaminen oikeakätisessä systeemissä johtaa vasenkätiseen systeemiin ja että kummankaan systeemin kiertäminen ei muuta sen ”kätisyyttä”. Koko kirjan ajan käytämme oikeakätistä systeemiä.
Kolmen muuttujan funktioiden kuvaajat ovat olemassa 4-ulotteisessa avaruudessa (eli \(\mathbb{R}^{4}\)), jota emme voi nähdä 3-ulotteisessa avaruudessamme, saati simuloida 2-ulotteisessa avaruudessa. Voimme siis ajatella 4-ulotteista avaruutta vain abstraktisti. Viihdyttävää keskustelua tästä aiheesta löytyy ABBOTin kirjasta.
Tähän mennessä olemme keskustelleet kohteen \(\textit{position}\) \(\textit{position}\) 2-dimensionaalisessa tai 3-dimensionaalisessa avaruudessa. Mutta entä esimerkiksi kappaleen nopeus tai kiihtyvyys? Tai kappaleeseen vaikuttava gravitaatiovoima? Näihin kaikkiin ilmiöihin näyttää liittyvän liikettä ja \(\textit{suunta}\) jollakin tavalla. Tähän liittyy ajatus \(\textit{vektori}\).
Olet jo käsitellyt nopeutta ja kiihtyvyyttä yhden muuttujan laskennassa. Esimerkiksi suoraa viivaa pitkin tapahtuvassa liikkeessä, jos \(y = f(t)\) antaa kappaleen siirtymän ajan \(t\) jälkeen, niin \(dy/dt = f\,'(t)\) on kappaleen nopeus hetkellä \(t\). Derivaatta \(f\,'(t)\) on vain luku, joka on positiivinen, jos kappale liikkuu sovittuun ”positiiviseen” suuntaan, ja negatiivinen, jos se liikkuu vastakkaiseen suuntaan. Voit siis ajatella, että kyseisellä luvulla, jota kutsuttiin esineen nopeudeksi, on kaksi komponenttia: \(\textit{magnitudi}\), joka on merkitty ei-negatiivisella luvulla ja jota edeltää suunta, joka on merkitty plus- tai miinussymbolilla (joka edustaa liikettä positiiviseen suuntaan tai negatiiviseen suuntaan), eli \(f\,'(t) = \pm a\) jollekin luvulle \(a \ge 0\). Tällöin \(a\) on nopeuden suuruus (jota tavallisesti kutsutaan kappaleen \(\textit{nopeus}\)), ja \(\pm\) edustaa nopeuden suuntaa (joskin \(+\) jätetään yleensä pois positiivisen suunnan osalta).
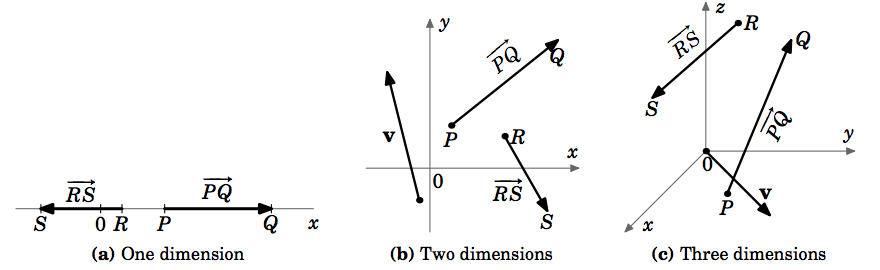
Jos liike tapahtuu suoraa viivaa pitkin eli yksiulotteisessa avaruudessa, myös nopeudet sisältyvät tuohon yksiulotteiseen avaruuteen, koska ne ovat vain lukuja. Yleisessä liikkeessä käyrää pitkin 2- tai 3-ulotteisessa avaruudessa nopeus on kuitenkin esitettävä moniulotteisella objektilla, jolla pitäisi olla sekä suuruus että suunta. Geometrinen objekti, jolla on nämä ominaisuudet, on nuoli, jota kutsutaan alkeisgeometriassa ”suunnatuksi viivasegmentiksi”. Tämä on motivaatio sille, miten määrittelemme vektorin.
Määritelmä 1. Vektorin määritelmä.1
(nollasta poikkeava) \(\textbf{vektori}\) on suunnattu viivasegmentti, joka on piirretty pisteestä \(P\) (jota kutsutaan sen \(\textbf{aloituspisteeksi}\)) pisteeseen \(Q\) (jota kutsutaan sen \(\textbf{loppupisteeksi}\)) siten, että \(P\) ja \(Q\) ovat erillisiä pisteitä. Vektoria merkitään \(\overrightarrow{PQ}\). Sen \(\textbf{magnitudi}\) on viivasegmentin pituus, jota merkitään \(\norm{\overrightarrow{PQ}}\), ja sen \(\textbf{suunta}\) on sama kuin suunnatun viivasegmentin pituus. \(\textbf{nollavektori}\) on vain piste, ja sitä merkitään \(\textbf{0}\).
Vektorin suunnan osoittamiseksi piirretään nuoli sen alkupisteestä sen loppupisteeseen. Usein merkitsemme vektorin yhdellä lihavoidulla kirjaimella (esim. \(\textbf{v}\)) ja käytämme termejä ”magnitudi” ja ”pituus” vaihdellen. Huomaa, että määritelmäämme voidaan soveltaa järjestelmiin, joilla on mikä tahansa määrä ulottuvuuksia (kuva 1.1.4 (a)-(c)).
Nollavektorista on huomattava muutama asia. Motivaatiomme siihen, mitä vektori on, sisälsi käsitteet suuruus ja suunta. Mikä on nollavektorin suuruus? Määrittelemme sen nollaksi eli \(\norm{\textbf{0}} = 0\). Tämä vastaa nollavektorin määritelmää, jonka mukaan nollavektori on vain piste, jonka pituus on nolla. Entä nollavektorin suunta? Yksittäisellä pisteellä ei todellakaan ole mitään hyvin määriteltyä suuntaa. Huomaa, että määrittelimme huolellisesti vain \(\textit{nolla}\)-vektorin suunnan, joka on hyvin määritelty, koska alku- ja loppupisteet ovat erilliset. Kaikki eivät ole yhtä mieltä nollavektorin suunnasta. Jotkut väittävät, että nollavektorilla on \(\textit{arbitrary}\) suunta (eli se voi ottaa minkä tahansa suunnan), jotkut sanovat, että sillä on \(\textit{määrittelemätön}\) suunta (eli suuntaa ei voida määrittää), kun taas toiset sanovat, että sillä on \(\textit{ei}\) suunta. Nollavektorin määritelmämme ei kuitenkaan edellytä, että sillä on suunta, ja jätämme sen siihen.
Nyt kun tiedämme, mikä vektori on, tarvitsemme keinon määrittää, milloin kaksi vektoria on yhtä suuri. Tämä johtaa meidät seuraavaan määritelmään.
Määritelmä 1.2
Kaksi nollasta poikkeavaa vektoria ovat \(\textbf{equal}\), jos niillä on sama suuruus ja sama suunta. Mikä tahansa vektori, jonka suuruus on nolla, on yhtä suuri kuin nollavektori.
Tämän määritelmän mukaan vektorit, joilla on sama suuruus ja suunta mutta eri alkupisteet, olisivat yhtä suuria. Esimerkiksi kuvassa 1.1.5 vektoreilla \(\textbf{u}\), \(\textbf{v}\) ja \(\textbf{w}\) on kaikilla sama suuruus \(\sqrt{5}\) (Pythagoraan lauseen mukaan). Näemme myös, että \(\textbf{u}\) ja \(\textbf{w}\) ovat yhdensuuntaisia, koska ne sijaitsevat suorilla, joilla on sama kaltevuus \(\frac{1}{2}\), ja ne osoittavat samaan suuntaan. Joten \(\textbf{u} = \textbf{w}\), vaikka niillä on eri alkupisteet. Näemme myös, että \(\textbf{v}\) on samansuuntainen kuin \(\textbf{u}\), mutta osoittaa vastakkaiseen suuntaan. Siis \(\textbf{u} \ne \textbf{v}\).
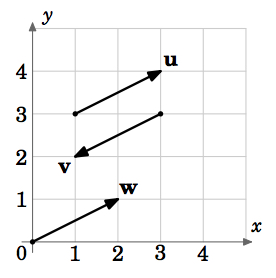
Voidaan siis nähdä, että tietylle suuruusluokalle ja suunnalle on olemassa ääretön määrä vektoreita, jotka ovat kaikki samanarvoisia ja jotka eroavat toisistaan vain alku- ja päätepisteidensä perusteella. Onko olemassa yksi ainoa vektori, jonka voimme valita edustamaan kaikkia näitä yhtäläisiä vektoreita? Vastaus on kyllä, ja siihen viittaa kuvan 1.1.5 vektori \(\textbf{w}\).
Jos ei toisin mainita, puhuttaessa ”vektorista”, jolla on tietty suuruus ja suunta, tarkoitamme vektoria, jonka alkupiste on koordinaatiston origossa.
Ajattelemalla vektoreiden alkupisteeksi origo tarjoaa tavan käsitellä vektoreita tavanomaisella tavalla, koska jokaisella koordinaatistolla on origo. On kuitenkin tilanteita, joissa on kätevää tarkastella vektorin eri alkupistettä (esimerkiksi laskettaessa vektoreita yhteen, mitä teemme seuraavassa kappaleessa). Toinen etu origon käyttämisestä alkupisteenä on se, että se tarjoaa helpon vastaavuuden vektorin ja sen päätepisteen välille.
Esimerkki 1.1
Olkoon \(\textbf{v}\) vektori \(\mathbb{R}^{3}\), jonka alkupiste on origossa ja jonka päätepiste on \((3,4,5)\). Vaikka \(\textit{point}\) \((3,4,5)\) ja vektori \(\textbf{v}\) ovat eri kohteita, on kätevää kirjoittaa \(\textbf{v} = (3,4,5)\). Näin tehtäessä ymmärretään, että \(\textbf{v}\) alkupiste on origossa \((0,0,0)\) ja loppupiste on \((3,4,5)\).
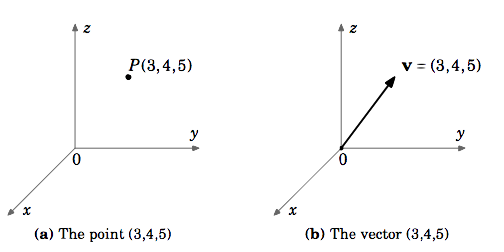
Jos ei toisin mainita, kun vektoreihin viitataan \(\textbf{v} = (a,b)\) kohdassa \(\mathbb{R}^{2}\) tai \(\textbf{v} = (a,b,c)\) kohdassa \(\mathbb{R}^{3}\), tarkoitamme vektoreita kartesiokoordinaateissa, jotka alkavat origosta. Kirjoitamme myös nollavektorin \(\textbf{0}\) \(\mathbb{R}^{2}\):ssa \(\mathbb{R}^{3}\):ssa \((0,0)\):ksi ja \((0,0,0,0)\): \((0,0,0)\):ksi.
Pistevektorien vastaavuus tarjoaa helpon tavan tarkastaa, ovatko kaksi vektoria yhtä suuria, ilman, että täytyy määritellä niiden suuruus ja suunta. Samoin kuin tarkastetaan, ovatko kaksi pistettä samat, tarkastetaan nyt, ovatko origosta alkavien vektoreiden päätepisteet samat. Etsi kullekin vektorille se (ainoa!) vektori, jonka kanssa se on yhtä suuri ja jonka alkupiste on origo. Vertaa sitten näiden ”uusien” vektoreiden päätepisteiden koordinaatteja: jos koordinaatit ovat samat, alkuperäiset vektorit ovat yhtä suuret. Jotta saat ”uudet” vektorit alkamaan origosta, \(\textit{translate}\) jokainen vektori aloitetaan origosta vähentämällä alkuperäisen alkupisteen koordinaatit alkuperäisestä päätepisteestä. Tuloksena oleva piste on sellaisen ”uusen” vektorin päätepiste, jonka alkupiste on origo. Tee tämä jokaiselle alkuperäiselle vektorille ja vertaa sitten.
Esimerkki 1.2
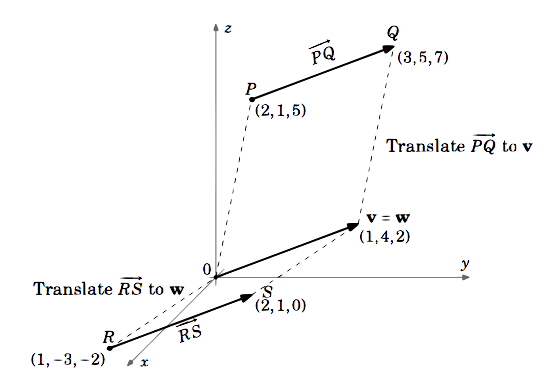
Tarkastellaan vektoreita \(\overrightarrow{PQ}\) ja \(\overrightarrow{RS}\) \(\mathbb{R}^{3}\), jossa \(P = (2,1,5), Q = (3,5,7), R = (1,-3,-2)\) ja \(S = (2,1,0)\). Onko \(\overrightarrow{PQ} = \overrightarrow{RS}\)?
Vektori \(\overrightarrow{PQ}\) on yhtä suuri kuin vektori \(\textbf{v}\), jonka alkupiste on \((0,0,0)\) ja päätepiste \(Q – P = (3,5,7) – (2,1,5) = (3 – 2,5 – 1,7 – 5) = (1,4,2)\).
Vastaavasti \(\overrightarrow{RS}\) on yhtä suuri kuin vektori \(\textbf{w}\), jonka alkupiste on \((0,0,0)\) ja päätepiste \(S – R = (2,1,0) – (1,-3,-2) = (2 – 1, 1 – (-3),0 – (-2)) = (1,4,2)\).
Siten \(\overrightarrow{PQ} = \textbf{v} = (1,4,2)\) ja \(\overrightarrow{RS} = \textbf{w} = (1,4,2)\).
\(\siten \overrightarrow{PQ} = \overrightarrow{RS}\)
Palautetaan mieleen euklidisen tason pisteiden etäisyyskaava:
Pisteiden \(P = (x_{1}, y_{1})\), \(Q = (x_{2}, y_{2})\) kohdalla \(\mathbb{R}^{2}\) etäisyys \(d\) pisteen \(P\) ja pisteen \(Q\) välillä on:
\
Tämän kaavan avulla saadaan seuraava tulos:
Huomautus
Vektorille \(\overrightarrow{PQ}\) \(\mathbb{R}^{2}\), jonka alkupiste on \(P = (x_{1}, y_{1})\) ja päätepiste \(Q = (x_{2}, y_{2})\), \(\overrightarrow{PQ}\) suuruus on:
\
Vektorin \(\textbf{v} = (a,b)\) suuruuden löytäminen \(\mathbb{R}^{2}\) on edellä olevan kaavan erikoistapaus, jossa \(P = (0,0)\) ja \(Q = (a,b)\):
Vektorille \(\textbf{v} = (a,b)\) \(\mathbb{R}^{2}\) \(\mathbb{R}^{2}\) on \(\textbf{v}\) suuruus:
\
Jotta voimme laskea vektoreiden suuruuden \(\(\mathbb{R}^{3}\):ssa, tarvitsemme etäisyyskaavan pisteille euklidisessa avaruudessa (lykkäämme todistuksen seuraavaan kappaleeseen):
Teoreema 1.1
Pisteiden \(P = (x_{1}, y_{1}, z_{1})\) ja \(Q = (x_{2}, y_{2}, z_{2})\) välinen etäisyys \(d\) \(\mathbb{R}^{3}\) on:
\
Todistuksessa käytetään seuraavaa tulosta:
Teoreema 1.2
Vektorille \(\textbf{v} = (a,b,c)\) \(\mathbb{R}^{3}\) \(\mathbb{R}^{3}\), \(\textbf{v}\) suuruus on:
\
Todistus: Tarkasteltavana on neljä tapausta:
\(\textit{Tapaus 1:}\) \(a = b = c = 0\). Silloin \(\textbf{v} = \textbf{0}\), joten \(\norm{\textbf{v}} = 0 = \sqrt{0^{2}} + 0^{2} + 0^{2}} = \sqrt{a^{2}} = \sqrt{a^{2}} + b^{2} + c^{2}}}\).
\(\textit{Tapaus 2:}\) \(\textit{tarkasti kaksi }\)\(a, b, c\) ovat \(0\). Yleisyyden menettämättä oletamme, että \(a = b = 0\) ja \(c \ne 0\) (kaksi muuta mahdollisuutta käsitellään samalla tavalla). Tällöin \(\textbf{v} = (0,0,c)\) on vektori, jonka pituus on \(|c|\) pitkin \(z\)-akselia. Joten \(\norm{\textbf{v}} = | c | = \sqrt{c^{2}} = \sqrt{0^{2}} + 0^{2} + c^{2}} = \sqrt{a^{2}}{2} + b^{2} + c^{2}}}\).
\(\textit{Tapaus 3:}\) \(\textit{täsmälleen yksi }\)\(a, b, c\) on \(0\). Yleisyyden menettämättä oletetaan, että \(a = 0\), \(b \ne 0\) ja \(c \ne 0\) (kaksi muuta mahdollisuutta käsitellään samalla tavalla). Tällöin \(\textbf{v} = (0,b,c)\), joka on vektori \(yz\)-tasossa, joten Pythagoraan lauseen mukaan on \(\norm{\textbf{v}} = \sqrt{b^{2}). + c^{2}} = \sqrt0^{2} + b^{2} + c^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}}\).
\(\textit{Tapaus 4:}\) \(\textit{ei yhtään }\)\(a, b, c\) ovat \(0\). Yleisyyden menettämättä voimme olettaa, että \(a, b, c\) ovat kaikki positiivisia (muut seitsemän mahdollisuutta käsitellään samalla tavalla). Tarkastellaan pisteitä \(P = (0,0,0)\), \(Q = (a,b,c)\), \(R =(a,b,0),\) ja \(S = (a,0,0)\) kuvan 1.1.8 mukaisesti. Soveltamalla Pythagoraan lauseketta suorakulmaiseen kolmioon \(\kolmio PSR\) saadaan \(\left\vert PR \right\vert^{2} = a^{2} + b^{2}\). Pythagoraan lauseen toinen soveltaminen, tällä kertaa suorakulmaiseen kolmioon \(\kolmio PQR\), antaa \(\norm{\textbf{v}} = \left\lvert PQ \right\rvert = \sqrt{\left\vert PR \right\vert^{2}). + \left\vert QR \right\vert^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}\). Tämä todistaa lauseen.
\(\tag{\(\textbf{QED}\)}\)
Esimerkki 1.3
Laske seuraavat:
- Vektorin \(\overrightarrow{PQ}\) suuruus \(\mathbb{R}^{2}\), jossa \(P = (-1,2)\) ja \(Q = (5,5)\).
\( \textit{Ratkaisu:}\) Kaavan (1.2) mukaan \(\norm{\overrightarrow{PQ}} = \sqrt{(5 – (-1))^{2} + (5 – 2)^{2}} = \sqrt{36 + 9} = \sqrt{45} = 3 \sqrt{5}\). - Vektorin \(\textbf{v} = (8,3)\) suuruus \(\mathbb{R}^{2}\).
\(\textit{Ratkaisu:}\) Kaavan (1.3) mukaan \(\norm{\textbf{v}} = \sqrt{8^{2} + 3^{2}}} = \sqrt{73}\). - Pisteiden \(P = (2, -1, 4)\) ja \(Q = (4, 2, -3)\) välinen etäisyys \(\mathbb{R}^{2}\).
\(\textit{Ratkaisu:}\) Kaavan (1.4) mukaan etäisyys \(d = \sqrt{(4 – 2)^{2}} + (2 – (-1))^{2} + (-3 – 4)^{2}} = \sqrt{4 + 9 + 49} = \sqrt{62}\). - Vektorin \(\textbf{v} = (5,8,-2)\) suuruus \(\mathbb{R}^{3}\) \(\mathbb{R}^{3}\).
\(\textit{Ratkaisu:}\) Kaavan (1.5) mukaan \(\norm{\textbf{v}} = \sqrt{5^{2}} + 8^{2} + (-2)^{2}} = \sqrt{25 + 64 + 4} = \sqrt{93}\).
Tekijät ja omistukset
-
Michael Corral (Schoolcraft College). Tämän sivun sisältö on jaettu GNU Free Documentation License, version 1.2 ehtojen mukaisesti.