Médias móveis em pandas

Introdução
Uma média móvel, também chamada de média móvel, é usada para analisar os dados da série temporal, calculando médias de diferentes subconjuntos do conjunto de dados completo. Como envolve tomar a média do conjunto de dados ao longo do tempo, também é chamada de média móvel (MM) ou média móvel.
Existem várias formas de calcular a média móvel, mas uma delas é tomar um subconjunto fixo de uma série completa de números. A primeira média móvel é calculada calculando a média do primeiro subconjunto fixo de números, e depois o subconjunto é alterado ao avançar para o subconjunto fixo seguinte (incluindo o valor futuro no subconjunto, excluindo o número anterior da série).
A média móvel é usada principalmente com dados de séries temporais para capturar as flutuações de curto prazo, enquanto se concentra em tendências mais longas.
A poucos exemplos de dados de séries cronológicas podem ser preços de ações, relatórios meteorológicos, qualidade do ar, produto interno bruto, emprego, etc.
Em geral, a média móvel suaviza os dados.
Moving average is a backbone to many algorithms, and one such algorithm is Autoregressive Integrated Moving Average Model (ARIMA), which uses moving average to make time series data predictions.
There are various types of moving average:
Simple Moving Average (SMA): A Média Móvel Simples (SMA) usa uma janela deslizante para obter a média ao longo de um determinado número de períodos de tempo. É uma média igualmente ponderada dos n dados anteriores.
Para entender melhor a SMA, vamos dar um exemplo, uma seqüência de n valores:

então a média móvel igualmente ponderada para n pontos de dados será essencialmente a média dos pontos de dados M anteriores, onde M é o tamanho da janela deslizante:

Simplesmente, para calcular os valores da média móvel seguinte, um novo valor será adicionado à soma, e o valor do período de tempo anterior será descartado, uma vez que você tem a média dos períodos de tempo anteriores, então a soma completa a cada vez não é necessária:

- Média móvel acumulada (CMA): Ao contrário da média móvel simples que baixa a observação mais antiga à medida que se adiciona a nova, a média móvel acumulada considera todas as observações anteriores. A CMA não é uma técnica muito boa para analisar tendências e suavizar os dados. A razão é que ela faz a média de todos os dados anteriores até o ponto de dados atual, portanto, uma média igualmente ponderada da seqüência de n valores:



- Média Móvel Exponencial (EMA): Ao contrário da SMA e CMA, a média móvel exponencial dá mais peso aos preços recentes e como resultado disso, pode ser um modelo melhor ou capturar melhor o movimento da tendência de uma forma mais rápida. A reação da EMA é diretamente proporcional ao padrão dos dados.
Desde que os EMAs dão mais peso aos dados recentes do que aos dados mais antigos, eles são mais sensíveis às últimas mudanças de preços em comparação com os SMAs, o que torna os resultados dos EMAs mais oportunos e, portanto, o EMA é mais preferido em relação a outras técnicas.
Suficiente de teoria, certo? Vamos saltar para a implementação prática da média móvel.
Implementando a Média Móvel em Dados de Séries Temporais
Média Móvel Simples (SMA)
Primeiro, vamos criar dados de séries temporais fictícias e tentar implementar a SMA usando apenas Python.
Confirme que existe uma demanda por um produto e que ele é observado por 12 meses (1 Ano), e você precisa encontrar médias móveis para períodos de janela de 3 e 4 meses.
Módulo de importação
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| mês | demanda | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Vamos calcular SMA para um tamanho de janela de 3, o que significa que você considerará três valores de cada vez para calcular a média móvel, e para cada novo valor, o valor mais antigo será ignorado.
Para implementar isto, você usará a função pandas iloc, já que a coluna demand é o que você precisa, você fixará a posição daquela na função iloc enquanto a linha será uma variável i a qual você manterá iterando até chegar ao fim do dataframe.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| mês | demanda | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Para uma verificação de sanidade, vamos também usar a função pandas in-built rolling e ver se corresponde com a nossa média móvel simples baseada em píton personalizada.
df = df.iloc.rolling(window=3).mean()df.head()| mês | demanda | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, para que você possa ver, as médias móveis personalizadas e pandas combinam exatamente, o que significa que sua implementação do SMA foi correta.
Vamos também calcular rapidamente a média móvel simples para um window_size de 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| mês | demanda | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 300 | 282.7 | 282.666667 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| mês | demanda | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 | 289.5 |
Agora, você vai plotar os dados das médias móveis que você calculou.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>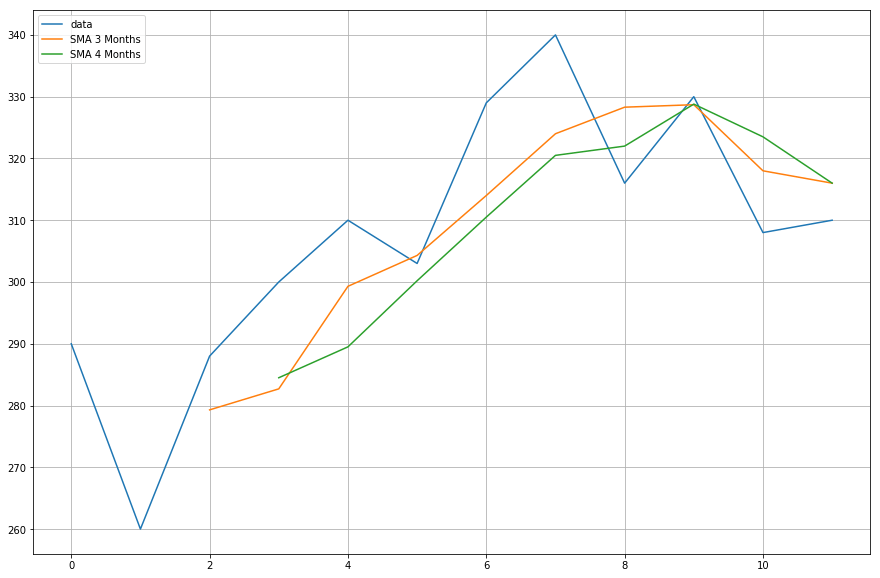
Média móvel acumulada
Acho que agora estamos prontos para mudar para um conjunto de dados real.
Para média móvel acumulada, vamos usar um air quality dataset que pode ser baixado deste link.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Data | Tempo | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
O pré-processamento é um passo essencial sempre que você estiver trabalhando com dados. Para dados numéricos uma das etapas mais comuns do pré-processamento é verificar por NaN (Null) valores. Se houver quaisquer NaN valores, você pode substituí-los por valores 0 ou média ou valores anteriores ou posteriores ou até mesmo deixá-los cair. Embora a substituição seja normalmente uma melhor escolha em vez de os deixar cair, uma vez que este conjunto de dados tem poucos valores NULL, deixá-los cair não afectará a continuidade da série.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64 Da saída acima, pode observar que existem cerca de 114 NaN valores em todas as colunas, no entanto irá descobrir que estão todos no final da série temporal, por isso vamos deixá-los cair rapidamente.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Você estará aplicando a média móvel acumulada no Temperature column (T), então vamos separar rapidamente aquela coluna dos dados completos.
df_T = pd.DataFrame(df.iloc)df_T.head()
Agora, você usará o método pandas expanding para encontrar a média acumulada dos dados acima. Se você se lembrar da introdução, ao contrário da média móvel simples, a média móvel cumulativa considera todos os valores anteriores ao calcular a média.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Os dados da série temporal são plotados com respeito à hora, então vamos combinar a coluna de data e hora e convertê-la em um objeto de data e hora. Para conseguir isso, você usará o módulo datetime de python (Fonte: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Vamos alterar o índice do temperature quadro de dados com datatime.
df_T.index = df.DateTimeVamos agora plotar a temperatura real e o tempo médio móvel acumulado.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Média móvel exponencial
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | ||
|---|---|---|---|---|
| DateTime | ||||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 | |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 | |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 | |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | |
| 2004-03-10 22:00:00 | 11.2 | 12,20 | 13,274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>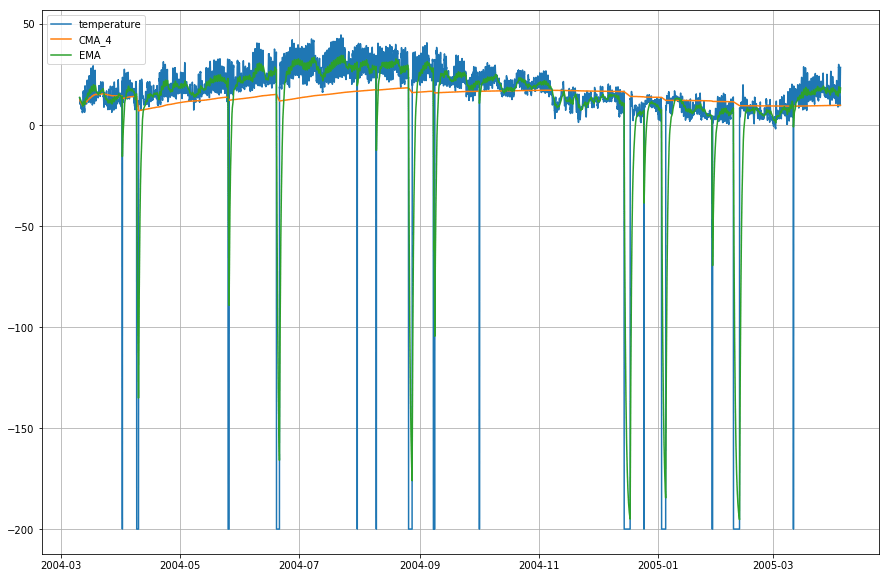
Wow! Então como você pode observar pelo gráfico acima, que o Exponential Moving Average (EMA) faz um excelente trabalho em capturar o padrão dos dados enquanto o Cumulative Moving Average (CMA) carece por uma margem considerável.
Vá além!
Congratulações ao terminar o tutorial.
Este tutorial foi um bom ponto de partida sobre como você pode calcular as médias móveis dos seus dados e fazer sentido.
Tente escrever o código python médio móvel cumulativo e exponencial sem usar a biblioteca pandas. Isso lhe dará um conhecimento muito mais profundo sobre como eles são calculados e de que maneiras eles são diferentes uns dos outros.
Ainda há muito a experimentar. Tente calcular a correlação automática parcial entre os dados de entrada e a média móvel, e tente encontrar alguma relação entre os dois.
Se você quiser aprender mais sobre DataFrames em pandas, faça o curso interativo DataCamp’s Foundations pandas.