Circuitos Digitais – De-Multiplexers
De-Multiplexer é um circuito combinado que realiza a operação inversa do Multiplexer. Possui uma única entrada, ‘n’ linhas de seleção e máximo de 2n de saídas. A entrada será conectada a uma destas saídas com base nos valores das linhas de seleção.
Desde que haja ‘n’ linhas de seleção, haverá 2n combinações possíveis de zeros e uns. Assim, cada combinação pode selecionar apenas uma saída. De-Multiplexer também é chamado como De-Mux.
1×4 De-Multiplexer
1×4 De-Multiplexer tem uma entrada I, duas linhas de seleção, s1 & s0 e quatro saídas Y3, Y2, Y1 &Y0. O diagrama de blocos de 1×4 De-Multiplexer é mostrado na figura seguinte.
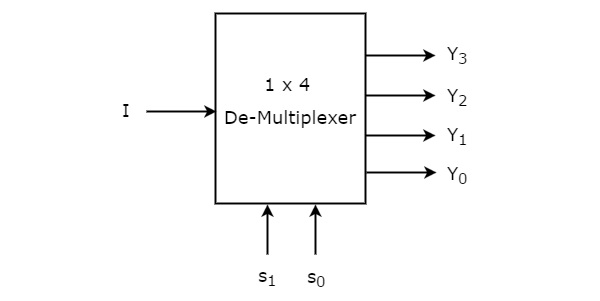
A entrada única ‘I’ será ligada a uma das quatro saídas, Y3 a Y0 com base nos valores das linhas de selecção s1 & s0. A tabela Verdade de 1×4 De-Multiplexer é mostrada abaixo.
| Entradas de seleção | Entradas | |||||
|---|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 | |
| 1 | 0 | 0 | I | 0 | 0 | |
| 1 | 1 | I | 0 | 0 | 0 | 0 |
Da tabela de Verdade acima, podemos escrever diretamente as funções booleanas para cada saída como
$$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}’I$$
$$$Y_{1}={s_{1}}’s_{0}I$$
$$$$Y_{0}={s_1}'{s_{0}}’I$$
Podemos implementar estas funções booleanas usando Inversores & 3-entrada E portões. O diagrama do circuito de 1×4 De-Multiplexer é mostrado na figura seguinte.
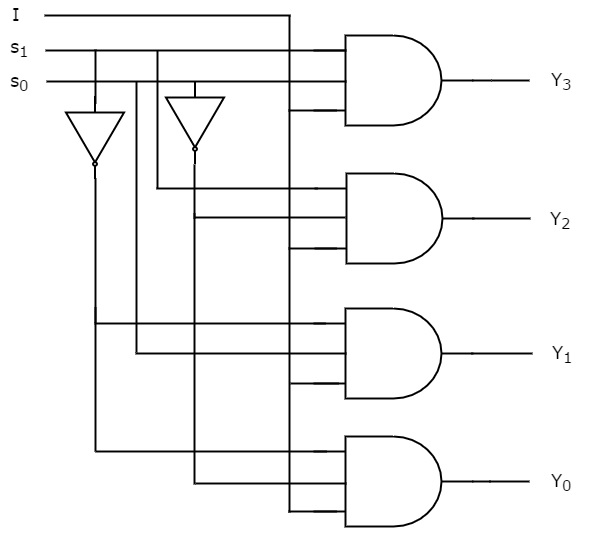
Pode ser facilmente entendido o funcionamento do circuito acima. Similarmente, você pode implementar 1×8 De-Multiplexer e 1×16 De-Multiplexer seguindo o mesmo procedimento.
Implementação de De-Multiplexers de Ordem Superior
Agora, vamos implementar os dois seguintes De-Multiplexers de ordem superior usando De-Multiplexers de ordem inferior.
1×8 De-Multiplexer
Nesta seção, vamos implementar 1×8 De-Multiplexer usando 1×4 De-Multiplexers e 1×2 De-Multiplexer. Sabemos que 1×4 De-Multiplexer tem uma única entrada, duas linhas de seleção e quatro saídas. Enquanto, 1×8 De-Multiplexer tem uma única entrada, três linhas de seleção e oito saídas.
Então, precisamos de dois 1×4 De-Multiplexers em segundo estágio para obter as oito saídas finais. Como o número de entradas no segundo estágio é dois, necessitamos de 1×2 DeMultiplexer no primeiro estágio para que as saídas do primeiro estágio sejam as entradas do segundo estágio. A entrada deste 1×2 De-Multiplexer será a entrada total de 1×8 De-Multiplexer.
Deixe o 1×8 De-Multiplexer ter uma entrada I, três linhas de seleção s2, s1 & s0 e saídas Y7 a Y0. A tabela Verdade do 1×8 De-Multiplexer é mostrada abaixo.
| Entradas de selecção | Entradas | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Podemos implementar 1×8 De-Multiplexador usando Multiplexadores de ordem inferior facilmente, considerando a tabela de Verdade acima. O diagrama de blocos do 1×8 De-Multiplexer é mostrado na figura seguinte.
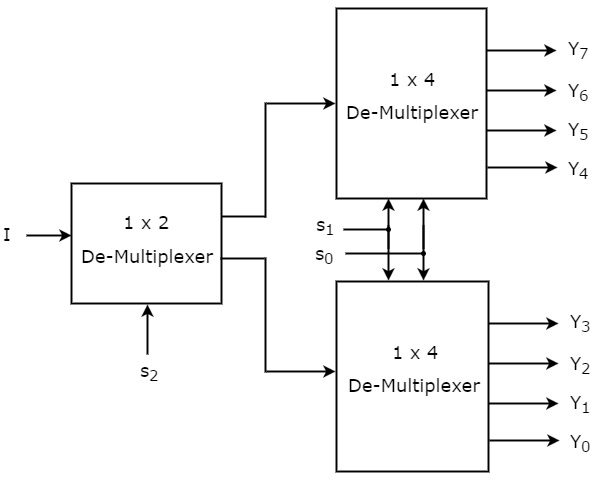
As linhas de seleção comuns, s1 & s0 são aplicadas a ambos os 1×4 De-Multiplexers. As saídas do 1×4 De-Multiplexer superior são Y7 a Y4 e as saídas do 1×4 De-Multiplexer inferior são Y3 a Y0.
A outra linha de selecção, s2 é aplicada ao 1×2 De-Multiplexer. Se s2 é zero, então uma das quatro saídas do 1×4 De-Multiplexer inferior será igual a entrada, I baseado nos valores das linhas de seleção s1 & s0. Da mesma forma, se s2 é uma, então uma das quatro saídas do 1×4 DeMultiplexer superior será igual a input, I baseado nos valores das linhas de seleção s1 & s0.
1×16 De-Multiplexer
Nesta seção, vamos implementar 1×16 De-Multiplexer usando 1×8 De-Multiplexers e 1×2 De-Multiplexer. Sabemos que 1×8 De-Multiplexer tem uma única entrada, três linhas de seleção e oito saídas. Enquanto, 1×16 De-Multiplexer tem entrada única, quatro linhas de seleção e dezesseis saídas.
Então, precisamos de dois 1×8 De-Multiplexers em segundo estágio para obter as dezesseis saídas finais. Como o número de entradas no segundo estágio é dois, necessitamos de 1×2 DeMultiplexer no primeiro estágio para que as saídas do primeiro estágio sejam as entradas do segundo estágio. A entrada deste 1×2 De-Multiplexer será a entrada total de 1×16 De-Multiplexer.
Deixe o 1×16 De-Multiplexer ter uma entrada I, quatro linhas de seleção s3, s2, s1 & s0 e saídas Y15 a Y0. O diagrama de blocos do 1×16 De-Multiplexer usando Multiplexadores de ordem inferior é mostrado na figura seguinte.
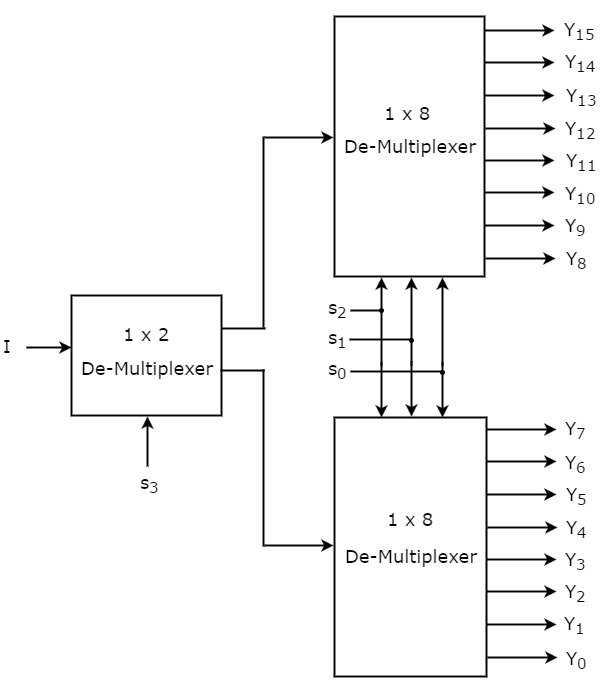
As linhas de seleção comuns s2, s1 & s0 são aplicadas a ambos os 1×8 De-Multiplexadores. As saídas do 1×8 De-Multiplexer superior são Y15 a Y8 e as saídas do 1×8 DeMultiplexer inferior são Y7 a Y0.
A outra linha de selecção, s3 é aplicada ao 1×2 De-Multiplexer. Se s3 for zero, então uma das oito saídas do De-Multiplexer 1×8 inferior será igual a entrada, I baseado nos valores das linhas de seleção s2, s1 & s0. Da mesma forma, se s3 é uma, então uma das 8 saídas do 1×8 De-Multiplexer superior será igual a input, I baseado nos valores das linhas de seleção s2, s1 & s0.