MCDM ou MCDA são acrônimos bem conhecidos para a tomada de decisão com múltiplos critérios e análise de decisão com múltiplos critérios; Stanley Zionts ajudou a popularizar a sigla com seu artigo “MCDM – If not a Roman Numeral, then What?” de 1979, destinado a um público empreendedor.

MCDM está preocupado em estruturar e resolver problemas de decisão e planejamento envolvendo múltiplos critérios. O objectivo é apoiar os decisores que enfrentam tais problemas. Normalmente, não existe uma solução óptima única para tais problemas e é necessário utilizar as preferências dos decisores para diferenciar as soluções.

“Resolver” pode ser interpretado de diferentes formas. Pode corresponder à escolha da “melhor” alternativa a partir de um conjunto de alternativas disponíveis (onde a “melhor” pode ser interpretada como “a alternativa mais preferida” de um tomador de decisão). Outra interpretação de “resolver” pode ser escolher um pequeno conjunto de boas alternativas, ou agrupar alternativas em diferentes conjuntos de preferências. Uma interpretação extrema poderia ser encontrar todas as alternativas “eficientes” ou “não dominadas” (que iremos definir em breve).

A dificuldade do problema tem origem na presença de mais do que um critério. Não há mais uma solução ótima única para um problema de MCDM que possa ser obtida sem incorporar informações de preferência. O conceito de uma solução ótima é freqüentemente substituído pelo conjunto de soluções não dominadas. Uma solução é chamada de não-dominada se não for possível melhorá-la em nenhum critério sem sacrificá-la em outro. Portanto, faz sentido que o tomador de decisão escolha uma solução a partir do conjunto não dominado. Caso contrário, ela/ele poderia fazer melhor em termos de alguns ou todos os critérios, e não fazer pior em nenhum deles. Geralmente, no entanto, o conjunto de soluções não dominadas é demasiado grande para ser apresentado ao decisor para a escolha final. Portanto, precisamos de ferramentas que ajudem o tomador de decisão a se concentrar nas soluções (ou alternativas) preferidas. Normalmente é preciso “trocar” certos critérios por outros.

MCDM tem sido uma área ativa de pesquisa desde os anos 70. Existem várias organizações relacionadas ao MCDM, incluindo a Sociedade Internacional para a Tomada de Decisão Multicritério, o Euro Working Group on MCDA, e a Secção INFORMS sobre o MCDM. Para uma história, veja: Köksalan, Wallenius e Zionts (2011).A MCDM recorre ao conhecimento em muitas áreas, incluindo:

• Matemática
• Análise de decisão
• Economia
• Tecnologia computacional
• Engenharia de software
• Sistemas de informação

Uma tipologiaEditar

Existem diferentes classificações de problemas e métodos de MCDM. Uma grande distinção entre problemas de MCDM é baseada em se as soluções estão explícita ou implicitamente definidas.

• Problemas de avaliação de múltiplos critérios: Estes problemas consistem de um número finito de alternativas, explicitamente conhecidas no início do processo de solução. Cada alternativa é representada pelo seu desempenho em múltiplos critérios. O problema pode ser definido como encontrar a melhor alternativa para um tomador de decisão (DM), ou encontrar um conjunto de boas alternativas. Também se pode estar interessado em “ordenar” ou “classificar” alternativas. Classificar refere-se a colocar alternativas em um conjunto de classes ordenadas por preferências (como atribuir classificações de crédito a países), e classificar refere-se a atribuir alternativas a conjuntos não ordenados (como diagnosticar pacientes com base em seus sintomas). Alguns dos métodos do MCDM nesta categoria foram estudados de forma comparativa no livro de Triantaphyllou sobre este assunto, 2000.
• Problemas de desenho de múltiplos critérios (problemas de programação matemática de múltiplos objetivos): Nesses problemas, as alternativas não são explicitamente conhecidas. Uma alternativa (solução) pode ser encontrada através da resolução de um modelo matemático. O número de alternativas é infinito (contável ou não) ou finito, mas tipicamente exponencialmente grande (no número de variáveis que variam sobre domínios finitos.)

Se for um problema de avaliação ou um problema de projeto, informações de preferência de DMs são necessárias para diferenciar entre soluções. Os métodos de solução para problemas de MCDM são geralmente classificados com base no tempo das informações de preferência obtidas do DM.

Existem métodos que requerem as informações de preferência do DM no início do processo, transformando o problema essencialmente em um problema de critério único. Diz-se que estes métodos operam por “articulação prévia de preferências”. Métodos baseados na estimativa de uma função de valor ou usando o conceito de “outranking relations”, processo de hierarquia analítica, e alguns métodos baseados em regras de decisão tentam resolver problemas de avaliação de múltiplos critérios utilizando a articulação prévia de preferências. Da mesma forma, existem métodos desenvolvidos para resolver problemas de desenho de critérios múltiplos utilizando a articulação prévia de preferências através da construção de uma função de valor. Talvez o mais conhecido desses métodos seja a programação de objetivos. Uma vez construída a função de valor, o programa matemático objetivo único resultante é resolvido para obter uma solução preferida.

Alguns métodos requerem informações de preferência da DM ao longo do processo de solução. Estes são chamados de métodos interativos ou métodos que requerem “articulação progressiva de preferências”. Estes métodos foram bem desenvolvidos tanto para a avaliação de critérios múltiplos (ver por exemplo Geoffrion, Dyer e Feinberg, 1972, e Köksalan e Sagala, 1995) como para problemas de design (ver Steuer, 1986).

Problemas de design com critérios múltiplos requerem tipicamente a solução de uma série de modelos de programação matemática de modo a revelar soluções implicitamente definidas. Para estes problemas, uma representação ou aproximação de “soluções eficientes” também pode ser de interesse. Esta categoria é referida como “articulação posterior de preferências”, implicando que o envolvimento da DM começa posterior à revelação explícita de soluções “interessantes” (ver por exemplo Karasakal e Köksalan, 2009).

Quando os modelos de programação matemática contêm variáveis inteiras, os problemas de desenho tornam-se mais difíceis de resolver. A Otimização Combinatória Multiobjetivo (MOCO) constitui uma categoria especial de tais problemas que apresentam dificuldades computacionais substanciais (ver Ehrgott e Gandibleux, 2002, para uma revisão).

Representações e definiçõesEditar

O problema MCDM pode ser representado no espaço de critério ou no espaço de decisão. Alternativamente, se diferentes critérios forem combinados por uma função linear ponderada, também é possível representar o problema no espaço de peso. Abaixo estão as demonstrações dos espaços de critério e de peso, bem como algumas definições formais.

Representação do espaço de critérioEditar

Deixe-nos assumir que avaliamos as soluções numa situação de problema específico utilizando vários critérios. Vamos ainda assumir que mais é melhor em cada critério. Então, entre todas as soluções possíveis, estamos idealmente interessados naquelas soluções que têm um bom desempenho em todos os critérios considerados. No entanto, é improvável que haja uma única solução que tenha um bom desempenho em todos os critérios considerados. Tipicamente, algumas soluções têm bom desempenho em alguns critérios e outras têm bom desempenho em outros. Encontrar uma forma de negociação entre critérios é um dos principais esforços na literatura do MCDM.

Matematicamente, o problema do MCDM correspondente aos argumentos acima pode ser representado como

“max” q sujeito a q ∈ Q

onde q é o vetor das funções do critério k (funções objetivas) e Q é o conjunto viável, Q ⊆ Rk.

Se Q é definido explicitamente (por um conjunto de alternativas), o problema resultante é chamado de problema de avaliação de múltiplos critérios.

Se Q é definido implicitamente (por um conjunto de restrições), o problema resultante é chamado de problema de projeto de múltiplos critérios.

As aspas são usadas para indicar que a maximização de um vetor não é uma operação matemática bem definida. Isto corresponde ao argumento de que teremos de encontrar uma forma de resolver o trade-off entre critérios (normalmente baseado nas preferências de um decisor) quando não existe uma solução que funcione bem em todos os critérios.

Representação do espaço de decisãoEditar

O espaço de decisão corresponde ao conjunto de possíveis decisões que estão disponíveis para nós. Os valores dos critérios serão consequências das decisões que tomarmos. Portanto, podemos definir um problema correspondente no espaço de decisão. Por exemplo, ao desenhar um produto, nós decidimos sobre os parâmetros de desenho (variáveis de decisão) cada um dos quais afeta as medidas de desempenho (critérios) com os quais avaliamos nosso produto.

Matematicamente, um problema de desenho de múltiplos critérios pode ser representado no espaço de decisão da seguinte forma:

max q = f ( x ) = f ( x 1 , … , x n ) sujeito a q ∈ Q = { f ( x ) : x ∈ X , X ⊆ R n } estilo de jogo q&=f(x)=f(x_{1},ldots ,x_{n}){\i1}{\i1}texto q&={f(x)=f(x)=f(x_{1},ldots ,x_{n})^^subseteq

onde X é o conjunto viável e x é o vector de decisão variável de tamanho n.

Um caso especial bem desenvolvido é obtido quando X é um poliedro definido por desigualdades lineares e igualdades. Se todas as funções objetivas são lineares em termos das variáveis de decisão, esta variação leva à programação linear objetiva múltipla (MOLP), uma subclasse importante dos problemas do MCDM.

Existem várias definições que são centrais no MCDM. Duas definições intimamente relacionadas são as de não-dominância (definidas com base no critério representação espacial) e eficiência (definidas com base na representação da variável de decisão).

Definição 1. q* ∈ Q é não dominada se não existir outra q ∈ Q tal que q ≥ q* e q ≠ q*.

Por outras palavras, uma solução é não dominada desde que não seja inferior a qualquer outra solução disponível em todos os critérios considerados.

Definição 2. x* ∈ X é eficiente se não existir outra x ∈ X tal que f(x) ≥ f(x*) e f(x) ≠ f(x*).

Se um problema de MCDM representa bem uma situação de decisão, então a solução mais preferida de um DM tem de ser uma solução eficiente no espaço de decisão, e a sua imagem é um ponto não dominado no espaço de critério. As seguintes definições também são importantes.

Definição 3. q* ∈ Q é fracamente não dominado se não existir outro q ∈ Q tal que q > q*.

Definição 4. x* ∈ X é fracamente eficiente se não existir outro x ∈ X tal que f(x) > f(x*).

Pontos fracos não dominados incluem todos os pontos não dominados e alguns pontos especiais dominados. A importância desses pontos dominados especiais vem do fato de que eles normalmente aparecem na prática e é necessário um cuidado especial para distingui-los dos pontos não dominados. Se, por exemplo, maximizarmos um único objectivo, podemos acabar por ter um ponto fraco não dominado que é dominado. Os pontos dominados do conjunto fracamente não dominado estão localizados em planos verticais ou horizontais (hiperplanos) no espaço do critério.

Ideal point: (no espaço do critério) representa o melhor (o máximo para problemas de maximização e o mínimo para problemas de minimização) de cada função objetiva e tipicamente corresponde a uma solução inviável.

Nadir point: (no espaço do critério) representa o pior (o mínimo para problemas de maximização e o máximo para problemas de minimização) de cada função objetiva entre os pontos do conjunto não dominado e é tipicamente um ponto dominado.

O ponto ideal e o ponto de nadir são úteis ao DM para obter a “sensação” da gama de soluções (embora não seja simples encontrar o ponto de nadir para problemas de projeto tendo mais de dois critérios).

Ilustrações dos espaços de decisão e critérioEditar

O seguinte problema de duas variáveis de MOLP no espaço da variável de decisão ajudará a demonstrar graficamente alguns dos conceitos chave.

max f 1 ( x ) = – x 1 + 2 x 2 max f 2 ( x ) = 2 x 1 – x 2 sujeito a x 1 ≤ 4 x 2 ≤ 4 x 1 + x 2 ≤ 7 – x 1 + x 2 ≤ 3 x 1 – x 2 ≤ 3 x 1 , x 2 ≥ 0 {\\i1}{\i1}({\i1}}(mathbf {\i} )&=-x_{\i}+2x_{\i}{\i}(mathbf {\i} )&=2x_{\i}-x_{2}{2}{2}{2}{2}{2}{2}{2}{2}{3}x_1476>leq 4}x_{2}&leq 4}x_{1}+x_{2}&leq 7}-x_{1}+x_{2}&leq 3}x_{1}-x_{2}&leq 3}x_{1},x_{2}&\geq 0\end{aligned}}}

Na Figura 1, os pontos extremos “e” e “b” maximizam o primeiro e o segundo objectivos, respectivamente. O limite vermelho entre esses dois pontos extremos representa o conjunto eficiente. Pode-se ver pela figura que, para qualquer solução viável fora do conjunto eficiente, é possível melhorar ambos os objetivos por alguns pontos no conjunto eficiente. Pelo contrário, para qualquer ponto do conjunto eficiente, não é possível melhorar ambos os objectivos avançando para qualquer outra solução viável. Nestas soluções, é preciso sacrificar de um dos objetivos para melhorar o outro objetivo.

Devido à sua simplicidade, o problema acima pode ser representado no espaço de critério substituindo os x’s pelos f’s da seguinte forma:

Max f1 Max f2 sujeito a f1 + 2f2 ≤ 12 2f1 + f2 ≤ 12 f1 + f2 ≤ 7 f1 – f2 ≤ 9 -f1 + f2 ≤ 9 f1 + f2 ≤ 9 f1 + 2f2 ≥ 0 2f1 + f2 ≥ 0

Apresentamos graficamente o espaço de critério na Figura 2. É mais fácil detectar os pontos não dominados (correspondentes a soluções eficientes no espaço de decisão) no espaço de critério. A região nordeste do espaço viável constitui o conjunto de pontos não dominados (para problemas de maximização).

Geração de soluções não dominadasEditar

Existem várias formas de gerar soluções não dominadas. Vamos discutir duas delas. A primeira abordagem pode gerar uma classe especial de soluções não dominadas enquanto a segunda abordagem pode gerar qualquer solução não dominada.

• Somas ponderadas (Gass & Saaty, 1955)

Se combinarmos os critérios múltiplos num único critério multiplicando cada critério com um peso positivo e somando os critérios ponderados, então a solução para o problema resultante do critério único é uma solução especialmente eficiente. Estas soluções eficientes especiais aparecem em pontos de canto do conjunto de soluções disponíveis. As soluções eficientes que não estão em pontos de canto têm características especiais e este método não é capaz de encontrar tais pontos. Matematicamente, podemos representar esta situação como

max wT.q = wT.f(x), w> 0 sujeito a x ∈ X

Variando os pesos, somas ponderadas podem ser usadas para gerar soluções eficientes de pontos extremos para problemas de projeto, e pontos suportados (convexos não dominados) para problemas de avaliação.

• Função escalarizante de realização (Wierzbicki, 1980)

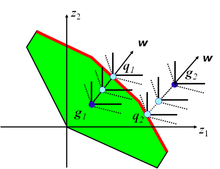
Achievement scalarizing functions também combinam múltiplos critérios em um único critério, ponderando-os de uma forma muito especial. Elas criam contornos retangulares que se afastam de um ponto de referência para as soluções eficientes disponíveis. Esta estrutura especial permite realizar funções de escalarização para alcançar qualquer solução eficiente. Esta é uma propriedade poderosa que torna estas funções muito úteis para problemas de MCDM.

Matematicamente, podemos representar o problema correspondente como

Min s(g, q, w, ρ) = Min {maxi + ρ ∑i (gi – qi)}, sujeito a q ∈ Q

A função de escalarização de realizações pode ser usada para projetar qualquer ponto (viável ou inviável) na fronteira eficiente. Qualquer ponto (suportado ou não) pode ser alcançado. O segundo termo na função objetivo é necessário para evitar a geração de soluções ineficientes. A Figura 3 demonstra como um ponto viável, g1, e um ponto inviável, g2, são projetados nos pontos não dominados, q1 e q2, respectivamente, ao longo da direção w usando uma função escalarizante de realização. Os contornos tracejados e sólidos correspondem aos contornos da função objetiva com e sem o segundo termo da função objetiva, respectivamente.

Resolver problemas de MCDMEditar

Desenvolveram-se diferentes escolas de pensamento para resolver problemas de MCDM (tanto do tipo de desenho como do tipo de avaliação). Para um estudo bibliométrico mostrando seu desenvolvimento ao longo do tempo, veja Bragge, Korhonen, H. Wallenius e J. Wallenius .

Escola de programação matemática de objetivos múltiplos

(1) Maximização vetorial: O propósito da maximização vetorial é aproximar o conjunto não dominado; originalmente desenvolvido para problemas de Programação Linear de Objetivos Múltiplos (Evans e Steuer, 1973; Yu e Zeleny, 1975).

(2) Programação interativa: Fases de computação alternam com fases de tomada de decisão (Benayoun et al., 1971; Geoffrion, Dyer e Feinberg, 1972; Zionts e Wallenius, 1976; Korhonen e Wallenius, 1988). Nenhum conhecimento explícito da função valor da DM é assumido.

Goal programming school

O propósito é estabelecer valores apriori para metas, e minimizar desvios ponderados dessas metas. Tanto pesos de importância como pesos lexicográficos preventivos foram usados (Charnes e Cooper, 1961).

Teóricos de conjuntos fuzzy

Conjuntos fuzzy foram introduzidos por Zadeh (1965) como uma extensão da noção clássica de conjuntos. Esta idéia é usada em muitos algoritmos MCDM para modelar e resolver problemas fuzzy.

Multi-atribute utility teorists

Multi-attribute utility ou value functions are elicited and used to identify the most preferred alternative or to rank order the alternatives. Técnicas elaboradas de entrevista, que existem para eliciar funções de utilidade aditiva linear e funções de utilidade não linear multiplicativa, são utilizadas (Keeney e Raiffa, 1976).

Escola francesa

A escola francesa foca na ajuda à decisão, em particular a família ELECTRE de métodos outranking que se originou na França durante a metade dos anos 60. O método foi inicialmente proposto por Bernard Roy (Roy, 1968).

Evolucionária escola de otimização multiobjetivo (EMO)

Os algoritmos EMO começam com uma população inicial, e o atualizam usando processos desenhados para imitar os princípios naturais de sobrevivência dos mais adequados e operadores de variação genética para melhorar a população média de uma geração para a próxima. O objetivo é convergir para uma população de soluções que representam o conjunto não dominado (Schaffer, 1984; Srinivas e Deb, 1994). Mais recentemente, há esforços para incorporar informações de preferência no processo de solução dos algoritmos EMO (ver Deb e Köksalan, 2010).

Métodos baseados na teoria dos sistemas cinzentos

Na década de 1980, Deng Julong propôs a Teoria do Sistema Cinzento (GST) e seu primeiro modelo de tomada de decisão com múltiplos atributos, chamado de modelo de análise relacional (GRA) de Deng Grey. Mais tarde, os estudiosos dos sistemas cinzentos propuseram muitos métodos baseados em GST como o modelo GRA Absoluto de Liu Sifeng, Grey Target Decision Making (GTDM) e Grey Absolute Decision Analysis (GADA).

Processo de hierarquia analítica (AHP)

O AHP primeiro decompõe o problema de decisão em uma hierarquia de sub-problemas. Em seguida, o decisor avalia a importância relativa dos seus vários elementos através de comparações de pares. A AHP converte essas avaliações em valores numéricos (pesos ou prioridades), que são usados para calcular uma pontuação para cada alternativa (Saaty, 1980). Um índice de consistência mede o grau de consistência da pessoa que toma a decisão nas suas respostas. AHP é uma das técnicas mais controversas listadas aqui, com alguns pesquisadores da comunidade MCDA acreditando que ela tem falhas. A matemática subjacente também é mais complicada, embora tenha ganho alguma popularidade como resultado de softwares comercialmente disponíveis.

Escritas em artigos gerais, a aplicação das técnicas de MCDM em várias disciplinas, como MCDM difuso, MCDM clássico, energia sustentável e renovável, técnica VIKOR, sistemas de transporte, qualidade de serviço, método TOPSIS, problemas de gerenciamento de energia, e-learning, turismo e hospitalidade, métodos SWARA e WASPAS.

Métodos MCDMEditar

Os seguintes métodos MCDM estão disponíveis, muitos dos quais são implementados por software especializado para a tomada de decisões:

• Método de Randomização de Índices Agregados (AIRM)
• Processo de hierarquia analítica (AHP)
• Processo de rede analítica (ANP)
• Processo de Feixe de Balanço
• Base…método critério (BCM)
• Melhor método (BWM)
• Modelo Brown-Gibson
• Melhor método (BWM)
• Melhor método (BWM)

>Melhor método (BWM)

• Melhor método (BWM) (CBA)
• Hierarquia de Valores Conjuntos (CVA)
• Análise de envelopamento de dados
• Decisão EXpert (DEX)
• Desagregação – Abordagens de Agregação (UTA*, UTAII, UTADIS)
• Conjunto rudimentar (Abordagem de conjunto rudimentar)
• Dominância-abordagem baseada em conjunto aproximado (DRSA)
• ELECTRE (Outranking)
• Avaliação baseada na Distância da Solução Média (EDAS)
• Abordagem de raciocínio evidente (ER)
• Programação de objectivos (GP)
• Análise relacional cinza (GRA)
• Produto interno de vetores (IPV)
• Medição da Atratividade por uma Técnica de Avaliação Baseada em Categorias (MACBETH)
• Multi-Attribute Rating Technique (SMART)
• Multi Critérios estratificados de tomada de decisão (SMCDM)
• Inferência Global de Qualidade Multi-Atributos (MAGIQ)
• Teoria da utilidade multiatributos (MAUT)
• Multi-teoria do valor do atributo (MAVT)
• Markovian Multi Criteria Decision Making
• Nova Abordagem à Avaliação (NATA)
• Nonstructural Fuzzy Decision Support System (NSFDSS)
• Potencialmente Todos os Rankings de pares de todas as alternativas possíveis (PAPRIKA)
• PROMETHEE (Outranking)
• Ranking baseado em pontos óptimos (RBOP)
• Análise de Aceitabilidade de Multicritérios Estocásticos (SMAA)
• Método de classificação de superioridade e inferioridade (método SIR)
• Técnica para a Ordem de Priorização por Semelhança à Solução Ideal (TOPSIS)
• Análise de valores (VA)
• Engenharia de valor (VE)
• Método VIKOR
• Modelo de produto ponderado (WPM)
• Modelo de soma ponderada (WSM)
• Modelo Integrado de Valor para Estruturas Sustentáveis (MIVES)