Mozgóátlagok a pandasban

Bevezetés
A mozgóátlagot, más néven gördülő vagy futó átlagot az idősoros adatok elemzésére használják a teljes adathalmaz különböző részhalmazainak átlagainak kiszámításával. Mivel az adathalmaz időbeli átlagát veszi, mozgó átlagnak (MM) vagy gördülő átlagnak is nevezik.
A gördülő átlag számításának különböző módjai vannak, de az egyik ilyen mód az, hogy a teljes számsorozatból egy rögzített részhalmazt veszünk. Az első mozgóátlagot a számok első rögzített részhalmazának átlagolásával számítják ki, majd a részhalmazt a következő rögzített részhalmazra való előrehaladással módosítják (a részhalmazba a jövőbeli értéket is bevonják, miközben az előző számot kizárják a sorozatból).
A mozgóátlagot leginkább idősoros adatoknál használják a rövid távú ingadozások megragadására, miközben a hosszabb trendekre összpontosítanak.
Az idősoros adatokra néhány példa lehet a részvényárfolyamok, az időjárás-jelentések, a levegő minősége, a bruttó hazai termék, a foglalkoztatás stb.
A mozgóátlag általában kisimítja az adatokat.
A mozgóátlag számos algoritmus gerincét képezi, és az egyik ilyen algoritmus az Autoregresszív Integrált Mozgóátlag Modell (ARIMA), amely mozgóátlagokat használ az idősoros adatok előrejelzéséhez.
A mozgóátlagoknak különböző típusai vannak:
-
Simple Moving Average (SMA): Az egyszerű mozgóátlag (SMA) egy csúszó ablakot használ az átlagoláshoz egy meghatározott számú időszakon keresztül. Ez az előző n adat egyenletesen súlyozott átlaga.
Az SMA további megértéséhez vegyünk egy példát, egy n értékből álló sorozatot:

akkor az n adatpontra vonatkozó egyenletesen súlyozott gördülő átlag lényegében az előző M adatpont átlaga lesz, ahol M a csúszóablak mérete:

Hasonlóképpen, az egymást követő gördülő átlagértékek kiszámításához egy új értéket adunk hozzá az összeghez, és az előző időszaki értéket elhagyjuk, mivel az előző időszakok átlagát kapjuk, így nem szükséges minden alkalommal teljes összegzés:

- Kumulatív mozgóátlag (CMA): Az egyszerű mozgóátlaggal ellentétben, amely a legrégebbi megfigyelést elhagyja, amikor az új megfigyelés hozzáadódik, a kumulatív mozgóátlag az összes korábbi megfigyelést figyelembe veszi. A CMA nem túl jó technika a trendek elemzésére és az adatok kisimítására. Ennek oka, hogy az összes korábbi adatot átlagolja az aktuális adatpontig, tehát az n értékek sorozatának egyformán súlyozott átlaga:



- Exponenciális mozgóátlag (EMA): Az SMA-tól és a CMA-tól eltérően az exponenciális mozgóátlag nagyobb súlyt ad a legutóbbi áraknak, és ennek eredményeképpen jobb modell lehet, vagy jobban megragadhatja a trend mozgását gyorsabb módon. Az EMA reakciója közvetlenül arányos az adatok mintázatával.
Mivel az EMA nagyobb súlyt ad a friss adatoknak, mint a régebbi adatoknak, az SMA-khoz képest jobban reagálnak a legújabb árváltozásokra, ami miatt az EMA-kból származó eredmények időszerűbbek, és ezért az EMA-t jobban preferálják más technikákkal szemben.
Elég az elméletből, igaz? Ugorjunk a mozgóátlag gyakorlati megvalósítására.
Mozgóátlagok megvalósítása idősoros adatokon
Simple Moving Average (SMA)
Először is hozzunk létre dummy idősoros adatokat, és próbáljuk meg az SMA megvalósítását csak Python segítségével.
Tegyük fel, hogy van egy termék iránti kereslet, és azt 12 hónapon keresztül (1 év) figyeljük, és mozgóátlagokat kell találnunk 3 és 4 hónapos ablakperiódusokra.
Import modul
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| hónap | kereslet | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Kalkuláljuk ki az SMA-t 3 ablakméretre, ami azt jelenti, hogy minden alkalommal három értéket veszünk figyelembe a mozgóátlag kiszámításához, és minden új értéknél a legrégebbi értéket figyelmen kívül hagyjuk.
A megvalósításhoz a pandas iloc függvényt fogja használni, mivel a demand oszlop az, amire szüksége van, ennek a pozícióját a iloc függvényben fogja rögzíteni, míg a sor egy i változó lesz, amelyet addig fog iterálni, amíg el nem éri az adatkeret végét.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| hónap | igény | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
A józansági ellenőrzéshez használjuk a pandas beépített rolling függvényt is, és nézzük meg, hogy egyezik-e az egyéni python alapú egyszerű mozgóátlagunkkal.
df = df.iloc.rolling(window=3).mean()df.head()| hónap | kereslet | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Klassz, tehát mint láthatod, az egyéni és a pandas mozgóátlagok pontosan egyeznek, ami azt jelenti, hogy az SMA implementációd helyes volt.
Legyen gyorsan kiszámolva az egyszerű mozgóátlag is egy window_size 4-es értékhez.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| hónap | kereslet | SMA_3 | pandasz_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| hónap | kereslet | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN | |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN | |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 | 289.5 |
Most a kiszámított mozgóátlagok adatait ábrázolja.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>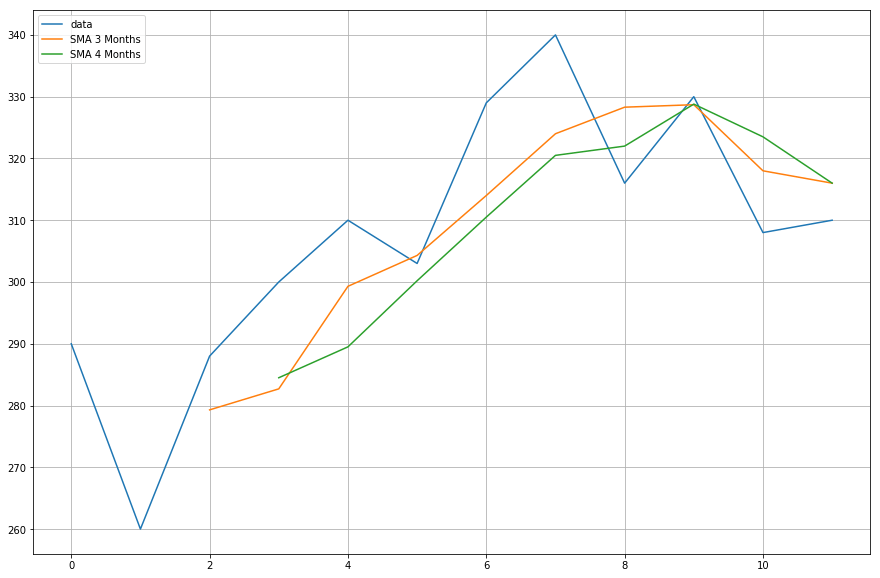
Kumulatív mozgóátlag
Úgy gondolom, most már készen állunk arra, hogy áttérjünk egy valós adatsorra.
A kumulatív mozgóátlaghoz használjunk egy air quality dataset, amely letölthető erről a linkről.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Az előfeldolgozás elengedhetetlen lépés, amikor adatokkal dolgozunk. Numerikus adatok esetében az egyik leggyakoribb előfeldolgozási lépés a NaN (Null) értékek ellenőrzése. Ha vannak NaN értékek, akkor azokat vagy 0-val vagy átlaggal, vagy az előző vagy az azt követő értékekkel helyettesíthetjük, vagy akár el is hagyhatjuk őket. Bár a helyettesítés általában jobb választás, mint az elhagyásuk, mivel ez az adatkészlet kevés NULL értéket tartalmaz, az elhagyásuk nem befolyásolja a sorozat folytonosságát.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64A fenti kimenetből megfigyelhetjük, hogy minden oszlopban körülbelül 114 NaN érték van, azonban ki fogjuk találni, hogy ezek mind az idősor végén vannak, ezért gyorsan hagyjuk el őket.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64A Temperature column (T) értékre kumulatív mozgóátlagot fogunk alkalmazni, ezért gyorsan válasszuk ki ezt az oszlopot a teljes adatból.
df_T = pd.DataFrame(df.iloc)df_T.head()
Most, a pandas expanding módszerrel meg fogod találni a fenti adatok kumulatív átlagát. Ha emlékszik a bevezetőből, az egyszerű mozgóátlaggal ellentétben a kumulatív mozgóátlag az összes előző értéket figyelembe veszi az átlag kiszámításakor.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Az idősoros adatokat az idő függvényében ábrázoljuk, ezért egyesítsük a dátum és az idő oszlopot és alakítsuk át datetime objektummá. Ehhez használjuk a python datetime modulját (Forrás: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Változtassuk meg a temperature adatkeret indexét datetime-ra.
df_T.index = df.DateTimeMost ábrázoljuk az aktuális hőmérsékletet és a kumulatív mozgóátlagot az idő függvényében.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponenciális mozgóátlag
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | ||
|---|---|---|---|---|
| DateTime | ||||
| 2004…03-10 18:00:00 | 13.6 | NaN | 13.600000 | |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 | |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 | |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>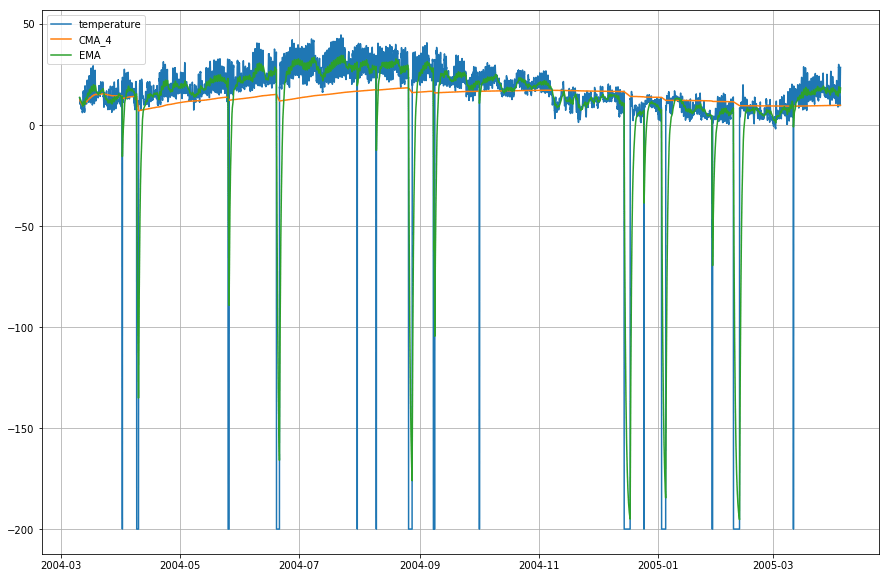
Wow! A fenti grafikonon tehát megfigyelhetjük, hogy a Exponential Moving Average (EMA) kiválóan érzékeli az adatok mintázatát, míg a Cumulative Moving Average (CMA) jelentős mértékben elmarad tőle.
Gyerünk tovább!
Gratulálunk a bemutató befejezéséhez.
Ez a bemutató jó kiindulópont volt ahhoz, hogyan lehet kiszámítani az adatok mozgóátlagait és értelmet adni nekik.
Kipróbálja megírni a kumulatív és exponenciális mozgóátlag python kódját a pandas könyvtár használata nélkül. Így sokkal mélyebb ismereteket szerezhetsz arról, hogyan számítják ki őket, és miben különböznek egymástól.
Még mindig van mit kísérletezni. Próbálja meg kiszámítani a részleges autokorrelációt a bemeneti adatok és a mozgóátlag között, és próbáljon meg valamilyen kapcsolatot találni a kettő között.
Ha többet szeretne megtudni a pandas DataFrames-ről, vegyen részt a DataCamp pandas Foundations interaktív kurzusán.
Még többet szeretne megtudni a pandas DataFrames-ről a pandasban?