De-Multiplexer je kombinační obvod, který provádí opačnou operaci Multiplexeru. Má jeden vstup, ‚n‘ selekčních linek a maximálně 2n výstupů. Vstup bude připojen k jednomu z těchto výstupů na základě hodnot výběrových řádků.

Protože existuje ‚n‘ výběrových řádků, bude existovat 2n možných kombinací nul a jedniček. Každá kombinace tedy může vybrat pouze jeden výstup. De-Multiplexer se také nazývá De-Mux.

1×4 De-Multiplexer

1×4 De-Multiplexer má jeden vstup I, dvě selekční linky, s1 & s0 a čtyři výstupy Y3, Y2, Y1 &Y0. Blokové schéma 1×4 De-Multiplexeru je znázorněno na následujícím obrázku.

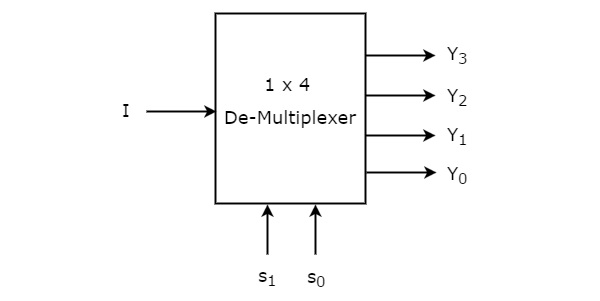
Jediný vstup „I“ bude připojen k jednomu ze čtyř výstupů, Y3 až Y0, na základě hodnot selekčních linek s1 & s0. Pravdivostní tabulka 1×4 De-Multiplexeru je uvedena níže.

Výběrové vstupy		Výstupy
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	I
0	1	0	0	I	0
1	0	0	I	0	0
1	1	I	0	0	0	0

Z výše uvedené pravdivostní tabulky, můžeme přímo zapsat logické funkce pro každý výstup jako

$$Y_{3}=s_{1}s_{0}I$$

$$Y_{2}=s_{1}{s_{0}}’I$$

$$Y_{1}={s_{1}}’s_{0}I$

$$Y_{0}={s_1}'{s_{0}}’I$$

Tyto logické funkce můžeme implementovat pomocí invertorů & 3-vstupních hradel AND. Schéma zapojení 1×4 De-Multiplexeru je znázorněno na následujícím obrázku.

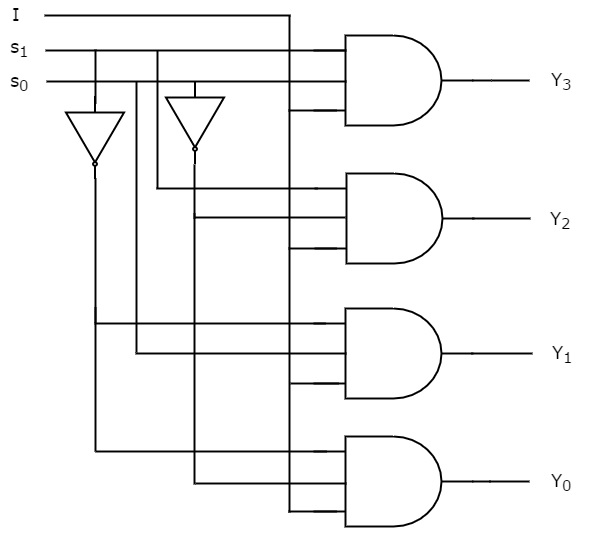
Snadno pochopíme činnost výše uvedeného obvodu. Podobně lze stejným postupem realizovat De-Multiplexer 1×8 a De-Multiplexer 1×16.

Implementace De-Multiplexerů vyššího řádu

Nyní realizujme následující dva De-Multiplexery vyššího řádu pomocí De-Multiplexerů nižšího řádu.

• 1×8 De-Multiplexer
• 1×16 De-Multiplexer

1×8 De-Multiplexer

V této části implementujme 1×8 De-Multiplexer pomocí 1×4 De-Multiplexerů a 1×2 De-Multiplexerů. Víme, že 1×4 De-Multiplexer má jeden vstup, dvě selekční linky a čtyři výstupy. Zatímco 1×8 De-Multiplexer má jeden vstup, tři selekční linky a osm výstupů.

V druhém stupni tedy potřebujeme dva 1×4 De-Multiplexery, abychom získali konečných osm výstupů. Protože počet vstupů ve druhém stupni je dva, potřebujeme v prvním stupni 1×2 DeMultiplexer, aby výstupy prvního stupně byly vstupy druhého stupně. Vstup tohoto 1×2 De-Multiplexeru bude celkovým vstupem 1×8 De-Multiplexeru.

Nechť má 1×8 De-Multiplexer jeden vstup I, tři selekční linky s2, s1 & s0 a výstupy Y7 až Y0. Pravdivostní tabulka 1×8 De-Multiplexeru je uvedena níže.

.

Výběrové vstupy			Výstupy
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

Můžeme implementovat 1×8 De-Multiplexer pomocí multiplexorů nižších řádů snadno s ohledem na výše uvedenou pravdivostní tabulku. Blokové schéma 1×8 De-Multiplexeru je znázorněno na následujícím obrázku.

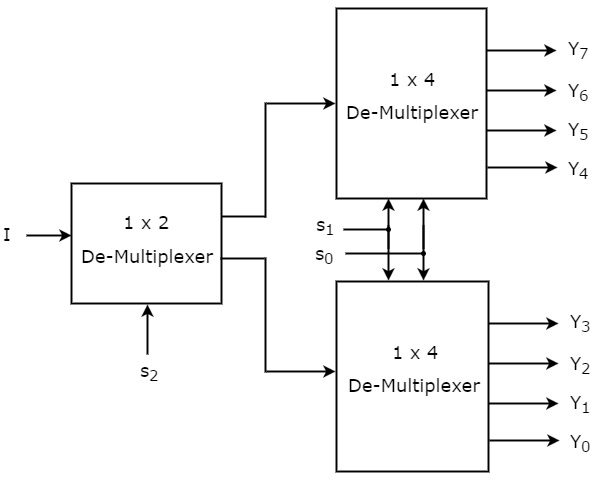
Společné selekční linky, s1 & s0 jsou aplikovány na oba 1×4 De-Multiplexery. Výstupy horního 1×4 De-Multiplexeru jsou Y7 až Y4 a výstupy dolního 1×4 De-Multiplexeru jsou Y3 až Y0.

Druhá selekční linka, s2 je aplikována na 1×2 De-Multiplexer. Je-li s2 nulová, pak jeden ze čtyř výstupů dolního 1×4 De-Multiplexeru bude roven vstupu, I na základě hodnot selekčních řádků s1 & s0. Podobně, je-li s2 rovna jedné, pak jeden ze čtyř výstupů horního 1×4 DeMultiplexeru bude roven vstupu, I na základě hodnot selekčních řádků s1 & s0.

1×16 De-Multiplexer

V této části implementujeme 1×16 De-Multiplexer pomocí 1×8 De-Multiplexerů a 1×2 De-Multiplexerů. Víme, že 1×8 De-Multiplexer má jeden vstup, tři selekční linky a osm výstupů. Zatímco 1×16 De-Multiplexer má jeden vstup, čtyři selekční linky a šestnáct výstupů.

V druhém stupni tedy potřebujeme dva 1×8 De-Multiplexery, abychom získali konečných šestnáct výstupů. Protože počet vstupů ve druhém stupni je dva, potřebujeme v prvním stupni 1×2 DeMultiplexer, aby výstupy prvního stupně byly vstupy druhého stupně. Vstup tohoto 1×2 De-Multiplexeru bude celkovým vstupem 1×16 De-Multiplexeru.

Nechť má 1×16 De-Multiplexer jeden vstup I, čtyři selekční linky s3, s2, s1 & s0 a výstupy Y15 až Y0. Blokové schéma 1×16 De-Multiplexeru s použitím Multiplexerů nižšího řádu je znázorněno na následujícím obrázku.

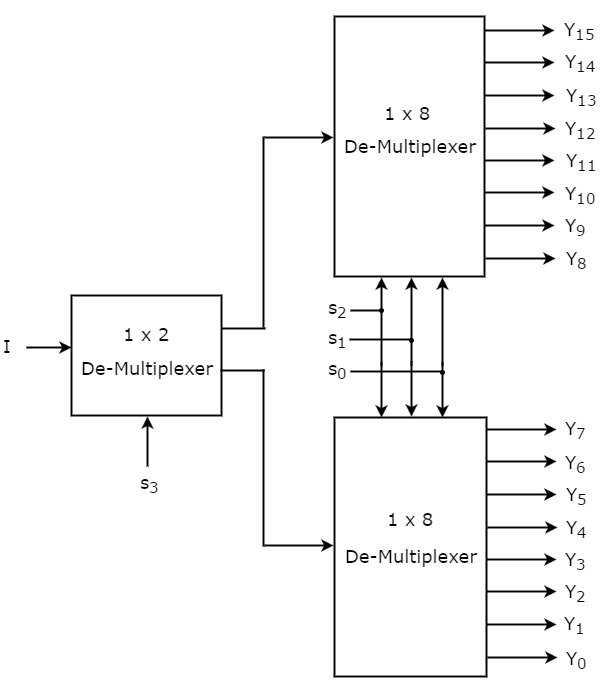
Společné selekční linky s2, s1 & s0 jsou aplikovány na oba 1×8 De-Multiplexery. Výstupy horního 1×8 De-Multiplexeru jsou Y15 až Y8 a výstupy dolního 1×8 DeMultiplexeru jsou Y7 až Y0.

Druhá selekční linka, s3, je přivedena na 1×2 De-Multiplexer. Je-li s3 nulová, pak jeden z osmi výstupů dolního 1×8 De-Multiplexeru bude roven vstupu, I na základě hodnot selekčních řádků s2, s1 & s0. Podobně, je-li s3 rovna jedné, pak jeden z osmi výstupů horního 1×8 De-Multiplexeru bude roven vstupu, I na základě hodnot selekčních řádků s2, s1 & s0.

.