Glidande medelvärden i pandas

Introduktion
Ett glidande medelvärde, även kallat rullande eller löpande medelvärde, används för att analysera tidsseriedata genom att beräkna medelvärden av olika delmängder av hela datasetet. Eftersom det handlar om att ta genomsnittet av datasetet över tiden kallas det också för rörligt medelvärde (MM) eller rullande medelvärde.
Det finns olika sätt att beräkna det rullande medelvärdet, men ett sådant sätt är att ta en fast delmängd från en komplett nummerserie. Det första glidande medelvärdet beräknas genom att medelvärdet av den första fasta delmängden av tal, och sedan ändras delmängden genom att gå framåt till nästa fasta delmängd (inkludera det framtida värdet i delmängden samtidigt som det föregående talet utesluts från serien).
Det glidande medelvärdet används oftast med tidsseriedata för att fånga upp kortsiktiga fluktuationer samtidigt som man fokuserar på längre trender.
Några exempel på tidsseriedata kan vara aktiekurser, väderleksrapporter, luftkvalitet, bruttonationalprodukt, sysselsättning etc.
I allmänhet jämnar det glidande medelvärdet ut data.
Det rörliga medelvärdet är en ryggrad i många algoritmer, och en sådan algoritm är Autoregressive Integrated Moving Average Model (ARIMA), som använder rörliga medelvärden för att göra förutsägelser om tidsseriedata.
Det finns olika typer av rörliga medelvärden:
-
Simple Moving Average (SMA): Simple Moving Average (SMA) använder ett glidande fönster för att ta genomsnittet över ett visst antal tidsperioder. Det är ett jämnt viktat medelvärde av de föregående n uppgifterna.
För att förstå SMA ytterligare, låt oss ta ett exempel, en sekvens av n värden:

då kommer det jämnt vägda rullande medelvärdet för n datapunkter i huvudsak att vara medelvärdet av de föregående M datapunkterna, där M är storleken på det glidande fönstret:

För beräkning av efterföljande rullande medelvärden kommer ett nytt värde att läggas till i summan, och värdet för föregående tidsperiod kommer att utelämnas, eftersom du har medelvärdet av tidigare tidsperioder så fullständig summering varje gång är inte nödvändig:

- Cumulative Moving Average (CMA): Till skillnad från det enkla glidande medelvärdet som släpper den äldsta observationen när den nya läggs till, tar det kumulativa glidande medelvärdet hänsyn till alla tidigare observationer. CMA är inte en särskilt bra teknik för att analysera trender och jämna ut data. Anledningen är att den tar ut medelvärdet av alla tidigare data fram till den aktuella datapunkten, alltså ett lika viktat medelvärde av sekvensen av n värden:




- Exponential Moving Average (EMA): Till skillnad från SMA och CMA ger exponentiellt glidande medelvärde mer vikt åt de senaste priserna och som ett resultat av detta kan det vara en bättre modell eller bättre fånga trendens rörelse på ett snabbare sätt. EMA:s reaktion är direkt proportionell mot datamönstret.
Då EMA ger en högre vikt åt nyare data än åt äldre data, reagerar de mer på de senaste prisförändringarna jämfört med SMA, vilket gör att resultaten från EMA är mer tidsenliga och därmed är EMA mer att föredra framför andra tekniker.
Tillräckligt med teori, eller hur? Låt oss hoppa till den praktiska implementeringen av det glidande medelvärdet.
Implementering av glidande medelvärde på tidsseriedata
Simple Moving Average (SMA)
Först ska vi skapa dummy tidsseriedata och prova att implementera SMA med hjälp av bara Python.
Antag att det finns en efterfrågan på en produkt och den observeras under 12 månader (1 år), och du behöver hitta glidande medelvärden för 3 och 4 månaders fönsterperioder.
Import module
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| månad | efterfrågan | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Låt oss beräkna SMA för en fönsterstorlek på 3, vilket innebär att du kommer att ta hänsyn till tre värden varje gång du beräknar det glidande medelvärdet, och för varje nytt värde kommer det äldsta värdet att ignoreras.
För att genomföra detta kommer du att använda pandas iloc-funktionen, eftersom demand-kolumnen är det du behöver kommer du att fastställa positionen för den i iloc-funktionen medan raden kommer att vara en variabel i som du kommer att fortsätta att iterera tills du når slutet av dataframeet.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| månad | efterfrågan | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
För en sanitetskontroll kan vi också använda den pandas inbyggda rolling-funktionen och se om den matchar vårt anpassade pythonbaserade enkla glidande medelvärde.
df = df.iloc.rolling(window=3).mean()df.head()| månad | efterfrågan | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.33333333 |
Cool, så som du kan se matchar de anpassade och pandas glidande medelvärdena exakt, vilket innebär att din implementering av SMA var korrekt.
Låt oss också snabbt beräkna det enkla glidande medelvärdet för ett window_size på 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| månad | efterfrågan | SMA_3 | pandas_SMA_3 | SMA_4 | ||
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | |
| 1 | 2 | 260 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.33333333 | NaN | |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| månad | efterfrågan | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.33333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.33333333 | 289.5 | 289.5 |
Nu ska du plotta data för de glidande medelvärdena som du beräknat.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>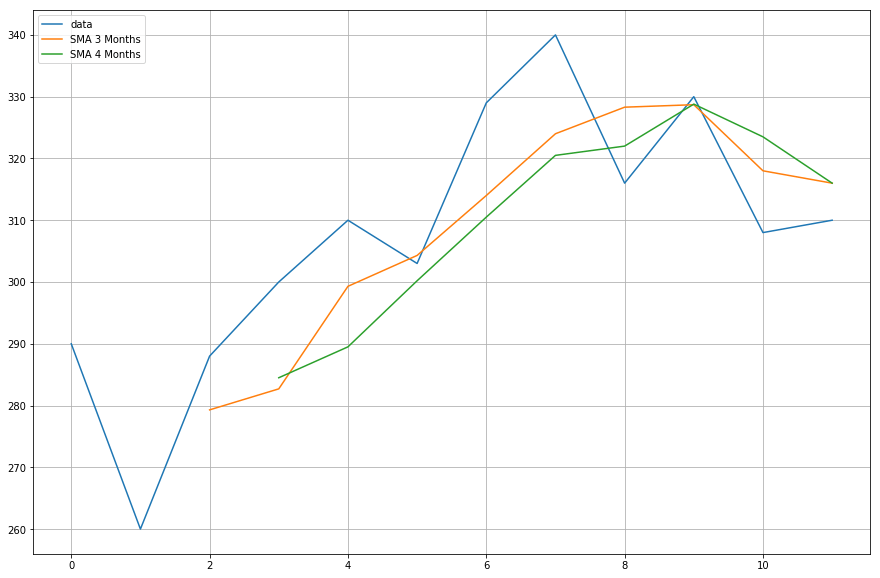
Kumulativt glidande medelvärde
Jag tror att vi nu är redo att gå över till ett riktigt dataset.
För kumulativt glidande medelvärde använder vi en air quality dataset som kan laddas ner från denna länk.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Förbehandling är ett viktigt steg när du arbetar med data. För numeriska data är ett av de vanligaste förbehandlingsstegen att kontrollera NaN (Null)-värden. Om det finns NaN-värden kan du ersätta dem med antingen 0 eller medelvärde eller föregående eller efterföljande värden eller till och med ta bort dem. Även om det normalt sett är bättre att ersätta än att släppa dem, eftersom det här datasetet har få NULL-värden, kommer det inte att påverka seriens kontinuitet att släppa dem.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Från ovanstående utdata kan du observera att det finns omkring 114 NaN-värden i alla kolumner, men du kommer att förstå att de alla ligger i slutet av tidsserien, så låt oss snabbt släppa dem.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Du kommer att tillämpa kumulativt glidande medelvärde på Temperature column (T), så låt oss snabbt separera den kolumnen från de fullständiga uppgifterna.
df_T = pd.DataFrame(df.iloc)df_T.head()
Nu, ska du använda pandas expanding-metoden för att hitta det kumulativa genomsnittet för ovanstående data. Om du minns från inledningen tar det kumulativa glidande medelvärdet, till skillnad från det enkla glidande medelvärdet, hänsyn till alla föregående värden när medelvärdet beräknas.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Tidsseriedata plottas med avseende på tiden, så låt oss kombinera kolumnen för datum och tid och omvandla den till ett datumtidsobjekt. För att uppnå detta använder du datetime-modulen från python (Källa: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Låt oss ändra indexet i temperature dataframe med datetime.
df_T.index = df.DateTimeLåt oss nu plotta den faktiska temperaturen och det kumulativa glidande medelvärdet i förhållande till tiden.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponentiellt glidande medelvärde
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | ||
|---|---|---|---|---|
| DateTime | ||||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 | |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 | |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 | |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>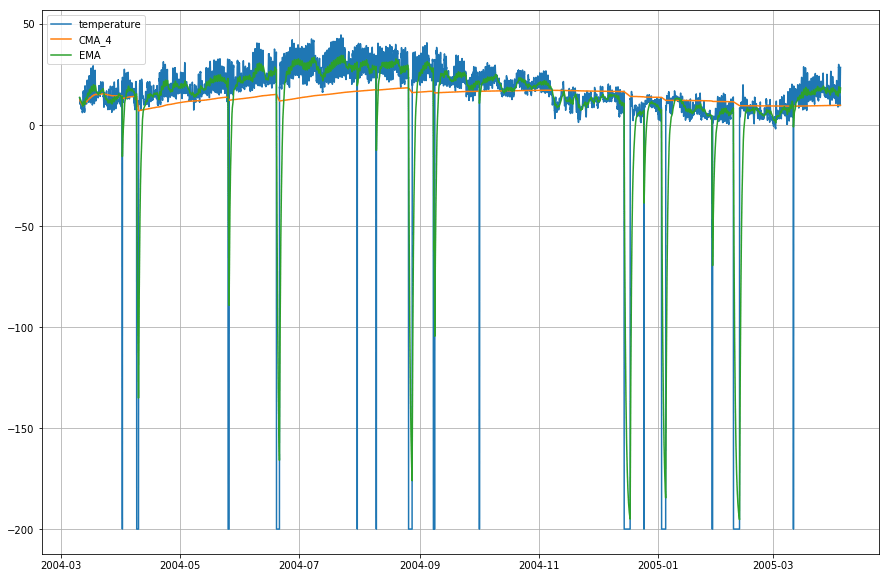
Wow! Så som du kan se i grafen ovan, gör Exponential Moving Average (EMA) ett utmärkt jobb när det gäller att fånga datamönstret, medan Cumulative Moving Average (CMA) saknar det med en avsevärd marginal.
Gå vidare!
Gratulerar dig till att du har avslutat handledningen.
Denna handledning var en bra utgångspunkt för hur du kan beräkna glidande medelvärden för dina data och göra det begripligt.
Try write the cumulative and exponential moving average python code without using the pandas library. Det kommer att ge dig mycket mer djupgående kunskap om hur de beräknas och på vilka sätt de skiljer sig från varandra.
Det finns fortfarande mycket att experimentera. Prova att beräkna den partiella autokorrelationen mellan indata och det glidande medelvärdet och försök att hitta något samband mellan de två.
Om du vill lära dig mer om DataFrames i pandas kan du gå DataCamps interaktiva kurs pandas Foundations.