Digitala kretsar – De-Multiplexer
De-Multiplexer är en kombinatorisk krets som utför den omvända operationen av Multiplexer. Den har en enda ingång, ”n” urvalsledningar och högst 2n utgångar. Ingången kopplas till en av dessa utgångar baserat på värdena på urvalslinjerna.
Eftersom det finns ”n” urvalslinjer kommer det att finnas 2n möjliga kombinationer av nollor och ettor. Så varje kombination kan bara välja en utgång. De-Multiplexer kallas också för De-Mux.
1×4 De-Multiplexer
1×4 De-Multiplexer har en ingång I, två urvalsledningar, s1 & s0 och fyra utgångar Y3, Y2, Y1 &Y0. Blockdiagrammet för 1×4 De-Multiplexer visas i följande figur.
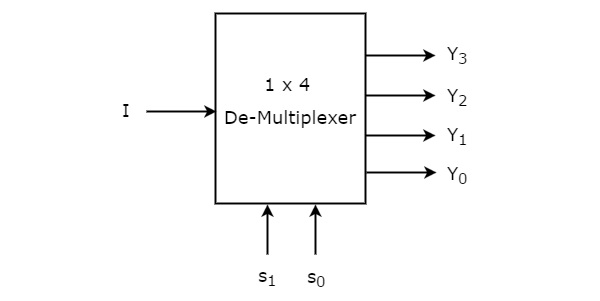
Den enda ingången ”I” kommer att anslutas till en av de fyra utgångarna, Y3 till Y0, baserat på värdena på urvalsledningarna s1 & s0. Sanningstabellen för 1×4 De-Multiplexer visas nedan.
| Väljningsingångar | Utgångar | |||||
|---|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I | |
| 0 | 1 | 0 | 0 | I | 0 | |
| 1 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 | |
Från sanningstabellen ovan, kan vi direkt skriva de booleska funktionerna för varje utgång som
$$Y_{3}=s_{1}s_{0}I$$
$$Y_{2}=s_{1}{s_{0}}’I$$
$$Y_{1}={s_{1}}}’s_{0}I$$$
$$Y_{0}={s_1}'{s_{0}}’I$$
Vi kan implementera dessa booleska funktioner med hjälp av inverterare & 3-ingångs- och AND-portar. Kretsschemat för 1×4 De-Multiplexer visas i följande figur.
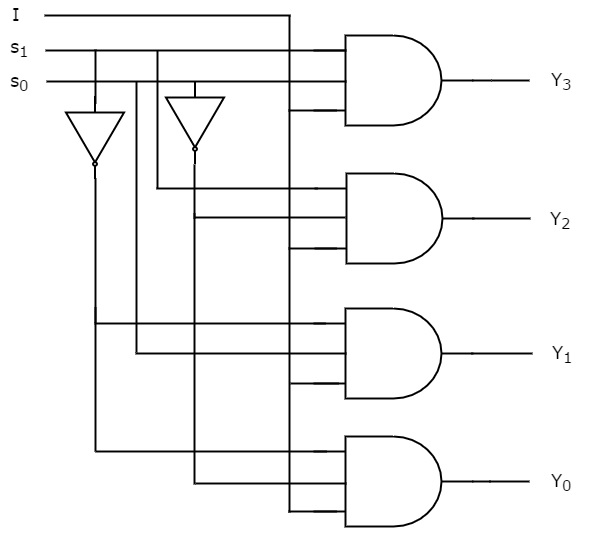
Vi kan lätt förstå hur ovanstående krets fungerar. På samma sätt kan du implementera 1×8 De-Multiplexer och 1×16 De-Multiplexer genom att följa samma procedur.
Implementering av De-Multiplexer av högre ordning
Nu ska vi implementera följande två De-Multiplexer av högre ordning med hjälp av De-Multiplexer av lägre ordning.
- 1×8 De-Multiplexer
- 1×16 De-Multiplexer
1×8 De-Multiplexer
I det här avsnittet ska vi implementera 1×8 De-Multiplexer med hjälp av 1×4 De-Multiplexer och 1×2 De-Multiplexer. Vi vet att 1×4 De-Multiplexer har en enda ingång, två urvalsledningar och fyra utgångar. Medan 1×8 De-Multiplexer har en enda ingång, tre urvalsledningar och åtta utgångar.
Så vi behöver två 1×4 De-Multiplexer i det andra steget för att få de slutliga åtta utgångarna. Eftersom antalet ingångar i det andra steget är två, behöver vi en 1×2 DeMultiplexer i det första steget så att utgångarna i det första steget blir ingångarna i det andra steget. Ingången till denna 1×2 De-Multiplexer kommer att vara den totala ingången till 1×8 De-Multiplexer.
Låt 1×8 De-Multiplexer ha en ingång I, tre urvalsledningar s2, s1 & s0 och utgångarna Y7 till Y0. Sanningstabellen för 1×8 De-Multiplexer visas nedan.
| Selektionsingångar | Utgångar | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Vi kan genomföra 1×8 De-Multiplexer med hjälp av multiplexer av lägre ordning enkelt genom att ta hänsyn till ovanstående sanningstabell. Blockdiagrammet för 1×8 De-Multiplexer visas i följande figur.
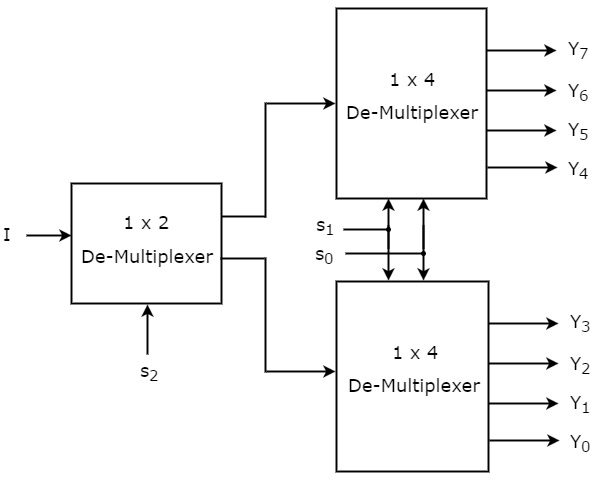
De gemensamma vallinjerna, s1 & s0 tillämpas på båda 1×4 De-Multiplexers. Utgångarna i den övre 1×4 De-Multiplexern är Y7 till Y4 och utgångarna i den nedre 1×4 De-Multiplexern är Y3 till Y0.
Den andra vallinjen, s2 tillämpas på 1×2 De-Multiplexern. Om s2 är noll kommer en av de fyra utgångarna i den nedre 1×4 De-Multiplexern att vara lika med ingången, I baserat på värdena för vallinjerna s1 & s0. På samma sätt, om s2 är ett, kommer en av de fyra utgångarna i den övre 1×4 DeMultiplexern att vara lika med ingången, I baserat på värdena för urvalslinjerna s1 & s0.
1×16 De-Multiplexer
I det här avsnittet ska vi implementera 1×16 De-Multiplexer med hjälp av 1×8 De-Multiplexer och 1×2 De-Multiplexer. Vi vet att 1×8 De-Multiplexer har en enda ingång, tre urvalsledningar och åtta utgångar. Medan 1×16 De-Multiplexer har en enda ingång, fyra urvalsledningar och sexton utgångar.
Så vi behöver två 1×8 De-Multiplexer i det andra steget för att få de slutliga sexton utgångarna. Eftersom antalet ingångar i det andra steget är två, behöver vi en 1×2 DeMultiplexer i det första steget så att utgångarna i det första steget blir ingångarna i det andra steget. Ingången till denna 1×2 De-Multiplexer kommer att vara den totala ingången till 1×16 De-Multiplexer.
Låt 1×16 De-Multiplexer ha en ingång I, fyra urvalsledningar s3, s2, s1 & s0 och utgångarna Y15 till Y0. Blockdiagrammet för 1×16 De-Multiplexer med hjälp av multiplexer av lägre ordning visas i följande figur.
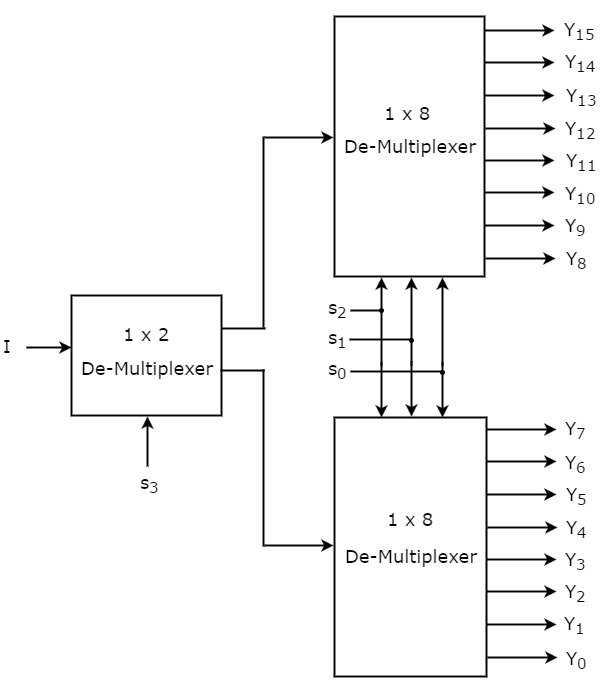
De gemensamma urvalslinjerna s2, s1 & s0 tillämpas på båda 1×8 De-Multiplexers. Utgångarna från den övre 1×8-demultiplexern är Y15 till Y8 och utgångarna från den nedre 1×8-demultiplexern är Y7 till Y0.
Den andra vallinjen, s3, används för 1×2 De-Multiplexer. Om s3 är noll kommer en av de åtta utgångarna i den nedre 1×8 De-Multiplexern att vara lika med ingången, I baserat på värdena för vallinjerna s2, s1 & s0. På samma sätt, om s3 är ett, kommer en av de åtta utgångarna i den övre 1×8 De-Multiplexern att vara lika med ingången, I baserat på värdena för urvalsledningarna s2, s1 & s0.