Denna artikel publicerades ursprungligen på Cadence’s webbplats. Den återges här med tillstånd från Cadence.

Konvolutionella neurala nätverk (CNN) används i stor utsträckning vid problem med mönster- och bildigenkänning eftersom de har ett antal fördelar jämfört med andra tekniker. Det här vitboken behandlar grunderna för CNNs, inklusive en beskrivning av de olika lager som används. Med hjälp av ett exempel på identifiering av trafikskyltar diskuterar vi utmaningarna med det allmänna problemet och presenterar algoritmer och implementeringsmjukvara som utvecklats av Cadence och som kan kompensera för beräkningsbörda och energi för en blygsam försämring av antalet identifierade skyltar. Vi beskriver utmaningarna med att använda CNN i inbyggda system och presenterar de viktigaste egenskaperna hos Cadence® Tensilica® Vision P5 digital signalprocessor (DSP) for Imaging and Computer Vision och mjukvara som gör den så lämplig för CNN-tillämpningar i många bildbehandlingsuppgifter och relaterade igenkänningsuppgifter.

Vad är ett CNN?

Ett neuralt nätverk är ett system av sammankopplade artificiella ”neuroner” som utbyter meddelanden mellan varandra. Förbindelserna har numeriska vikter som justeras under träningsprocessen, så att ett korrekt tränat nätverk reagerar korrekt när det får en bild eller ett mönster att känna igen. Nätverket består av flera lager av ”neuroner” som upptäcker egenskaper. Varje lager har många neuroner som reagerar på olika kombinationer av inmatningar från de föregående lagren. Som framgår av figur 1 är lagren uppbyggda så att det första lagret upptäcker en uppsättning primitiva mönster i inmatningen, det andra lagret upptäcker mönster av mönster, det tredje lagret upptäcker mönster av dessa mönster och så vidare. Typiska CNN använder 5 till 25 olika lager för mönsterigenkänning.

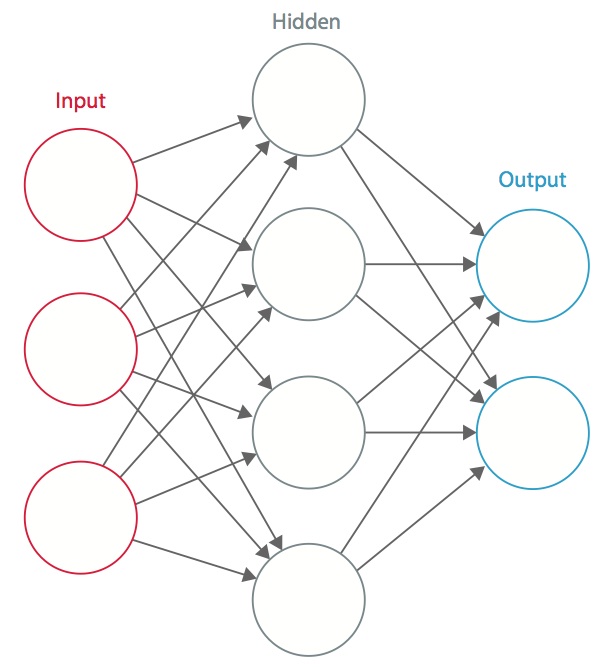
Figur 1: Ett artificiellt neuralt nätverk

Träning utförs med hjälp av en ”märkt” datamängd av inmatningar i ett brett sortiment av representativa inmatningsmönster som är märkta med deras avsedda utgångssvar. Vid träningen används allmänna metoder för att iterativt bestämma vikterna för mellanliggande och slutliga funktionsneuroner. Figur 2 visar träningsprocessen på blocknivå.

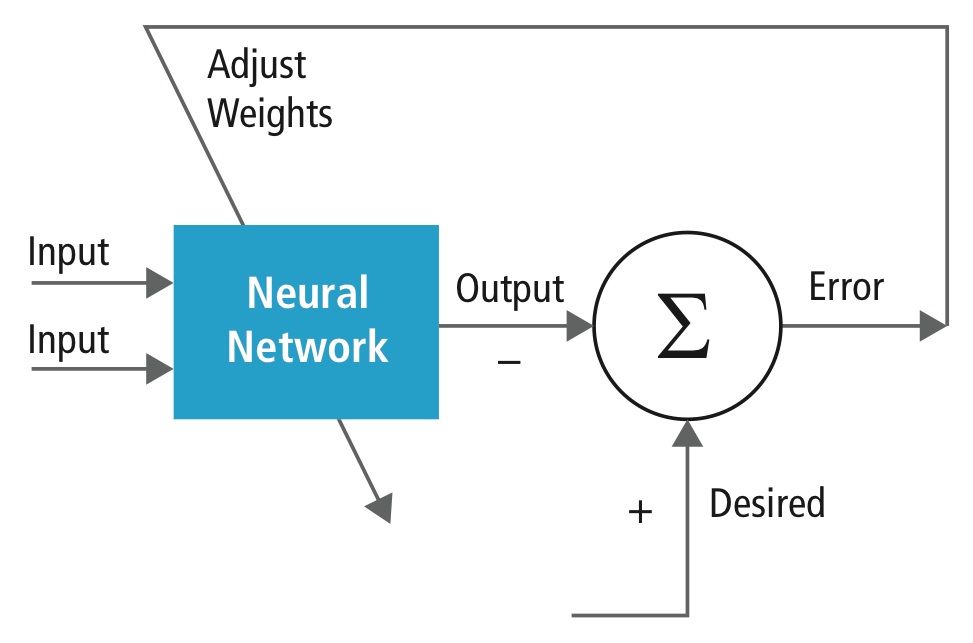
Figur 2: Träning av neurala nätverk

Neurala nätverk är inspirerade av biologiska neurala system. Den grundläggande beräkningsenheten i hjärnan är en neuron och de är sammankopplade med synapser. I figur 3 jämförs en biologisk neuron med en grundläggande matematisk modell .

Figur 3: Illustration av en biologisk neuron (överst) och dess matematiska modell (nederst)

I ett verkligt djuriskt nervsystem uppfattas en neuron som att den tar emot inmatningssignaler från sina dendriter och producerar utmatningssignaler längs sin axon. Axonet förgrenar sig och ansluter sig via synapser till andra neuroners dendriter. När kombinationen av ingångssignaler når ett visst tröskeltillstånd bland dess ingångsdendriter utlöses neuronen och dess aktivering kommuniceras till efterföljande neuroner.

I beräkningsmodellen för det neurala nätverket interagerar signalerna som färdas längs axonerna (t.ex. x0) multiplikativt (t.ex. w0x0) med den andra neuronens dendriter baserat på den synaptiska styrkan vid den synapsen (t.ex. w0). Synaptiska vikter är inlärningsbara och styr inflytandet från en neuron till en annan. Dendriterna bär signalen till cellkroppen, där alla signaler summeras. Om den slutliga summan ligger över ett visst tröskelvärde utlöses neuronen och skickar en spik längs sin axon. I beräkningsmodellen antas det att den exakta tidpunkten för avfyrningen inte spelar någon roll och att det endast är avfyrningsfrekvensen som förmedlar information. Med utgångspunkt i tolkningen av frekvenskoden modelleras neuronens avfyrningsfrekvens med en aktiveringsfunktion ƒ som representerar frekvensen av spikar längs axonet. Ett vanligt val av aktiveringsfunktion är sigmoid. Sammanfattningsvis beräknar varje neuron punktprodukten av ingångar och vikter, lägger till bias och tillämpar icke-linjäritet som en aktiveringsfunktion (t.ex. enligt en sigmoid responsfunktion).

Ett CNN är ett specialfall av det neurala nätverk som beskrivs ovan. Ett CNN består av ett eller flera konvolutionella lager, ofta med ett lager för subsampling, som följs av ett eller flera fullt sammankopplade lager som i ett vanligt neuralt nätverk.

Designen av ett CNN motiveras av upptäckten av en visuell mekanism, den visuella cortexen, i hjärnan. Den visuella cortexen innehåller en mängd celler som ansvarar för att upptäcka ljus i små, överlappande delområden av synfältet, som kallas receptiva fält. Dessa celler fungerar som lokala filter över det inkommande rummet, och de mer komplexa cellerna har större receptiva fält. Konvolutionslagret i en CNN utför den funktion som utförs av cellerna i den visuella cortexen .

En typisk CNN för att känna igen trafikskyltar visas i figur 4. Varje funktion i ett lager tar emot indata från en uppsättning funktioner som ligger i ett litet grannskap i det föregående lagret som kallas ett lokalt receptivt fält. Med lokala receptiva fält kan funktionerna extrahera elementära visuella funktioner, t.ex. orienterade kanter, ändpunkter, hörn osv. som sedan kombineras av de högre lagren.

I den traditionella modellen för mönster- och bildigenkänning samlar en handdesignad funktionsextraherare in relevant information från inmatningen och eliminerar irrelevanta variabiliteter. Extraktorn följs av en träningsbar klassificerare, ett standard neuralt nätverk som klassificerar funktionsvektorer i klasser.

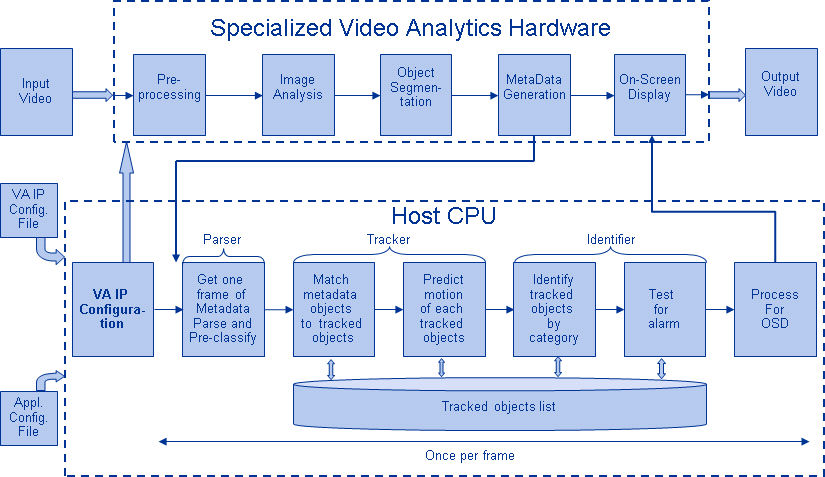
I ett CNN spelar konvolutionslagren rollen som funktionsextraktor. Men de är inte utformade för hand. Vikter för konvolutionsfiltrets kärnor bestäms som en del av träningsprocessen. Konvolutionslagren kan extrahera de lokala egenskaperna eftersom de begränsar de dolda lagrens receptiva fält till att vara lokala.

Figur 4: Typiskt blockdiagram för en CNN

CNN används inom en mängd olika områden, bland annat bild- och mönsterigenkänning, taligenkänning, behandling av naturliga språk och videoanalys. Det finns ett antal anledningar till att konvolutionella neurala nätverk blir viktiga. I traditionella modeller för mönsterigenkänning utformas funktionsextraktorer för hand. I CNN:er bestäms vikterna för det konvolutionella lagret som används för extraktion av funktioner och för det fullt anslutna lagret som används för klassificering under träningsprocessen. CNN:s förbättrade nätverksstrukturer leder till besparingar i fråga om minneskrav och krav på beräkningskomplexitet och ger samtidigt bättre prestanda för tillämpningar där indata har lokal korrelation (t.ex. bild och tal).

De stora kraven på beräkningsresurser för träning och utvärdering av CNN:s tillgodoses ibland av grafikprocessorer (GPU:er), DSP:er eller andra kiselarkitekturer som är optimerade för hög genomströmning och låg energiförbrukning när de idiosynkratiska mönstren för CNN-beräkningar utförs. Faktum är att avancerade processorer som Tensilica Vision P5 DSP for Imaging and Computer Vision från Cadence har en nästan idealisk uppsättning beräknings- och minnesresurser som krävs för att köra CNN med hög effektivitet.

I tillämpningar för mönster- och bildigenkänning har bästa möjliga korrekta detektionsfrekvens (CDR) uppnåtts med hjälp av CNN. CNN har till exempel uppnått en CDR på 99,77 % med MNIST-databasen med handskrivna siffror , en CDR på 97,47 % med NORB-databasen med 3D-objekt och en CDR på 97,6 % på ~5600 bilder med mer än 10 objekt . CNN ger inte bara den bästa prestandan jämfört med andra detekteringsalgoritmer, de överträffar till och med människor i fall som klassificering av objekt i finkorniga kategorier, t.ex. en viss hundras eller fågelart .

Figur 5 visar en typisk pipeline för en visionsalgoritm, som består av fyra steg: förbearbetning av bilden, detektering av intressanta regioner (ROI) som innehåller sannolika objekt, objektigenkänning och beslutsfattande i visionen. Förbehandlingssteget är vanligtvis beroende av detaljerna i inmatningen, särskilt kamerasystemet, och implementeras ofta i en fast ansluten enhet utanför visionssubsystemet. Beslutsfattandet i slutet av pipelinen arbetar vanligtvis med erkända objekt-Det kan fatta komplexa beslut, men det arbetar med mycket mindre data, så dessa beslut är vanligtvis inte beräkningsmässigt svåra eller minneskrävande problem. Den stora utmaningen ligger i skedena för objektsdetektering och igenkänning, där CNNs nu får ett stort genomslag.

Figur 5: Pipeline för visionsalgoritmer

Lager av CNNs

Då flera och olika lager staplas på varandra i en CNN, byggs komplexa arkitekturer för klassificeringsproblem. Fyra typer av lager är vanligast: konvolutionslager, pooling/subsamplinglager, icke-linjära lager och fullt anslutna lager.

Konvolutionslager

Konvolutionen extraherar olika egenskaper hos indata. Det första konvolutionslagret extraherar egenskaper på låg nivå som kanter, linjer och hörn. Lager på högre nivå extraherar funktioner på högre nivå. Figur 6 illustrerar processen för 3D-falsning som används i CNN:er. Inmatningen har storleken N x N x D och konvolveras med H kärnor, var och en med storleken k x k x D separat. Konvolution av en indata med en kärna ger en utgångsfunktion, och med H kärnor oberoende av varandra ger H funktioner. Med utgångspunkt från det övre vänstra hörnet av inmatningen flyttas varje kärna från vänster till höger, ett element i taget. När det övre högra hörnet har nåtts flyttas kärnan ett element nedåt, och återigen flyttas kärnan från vänster till höger, ett element i taget. Denna process upprepas tills
kärnan når det nedre högra hörnet. För fallet när N = 32 och k = 5 finns det 28 unika positioner från vänster till höger och 28 unika positioner från uppåt till nedåt som kärnan kan ta. Varje funktion i resultatet kommer att innehålla 28×28 (dvs. (N-k+1) x (N-k+1)) element som motsvarar dessa positioner. För varje position för kärnan i en process med glidande fönster multipliceras och ackumuleras k x k x D-element av indata och k x k x D-element av kärnan element för element. Så för att skapa ett element av en utgångsfunktion krävs k x k x D multiplikations- och ackumuleringsoperationer.

Figur 6: Bildlig representation av konvolutionsprocessen

Pooling/subsamplingskikt

Pooling/subsamplingskiktet minskar upplösningen av funktionerna. Det gör funktionerna robusta mot brus och förvrängning. Det finns två sätt att göra pooling: max pooling och average pooling. I båda fallen delas inmatningen in i icke överlappande tvådimensionella utrymmen. I figur 4 är till exempel lager 2 poolningslagret. Varje inmatningsfunktion är 28×28 och delas upp i 14×14 områden av storleken 2×2. För genomsnittlig pooling beräknas genomsnittet av de fyra värdena i regionen. För max pooling väljs det högsta värdet av de fyra värdena.

Figur 7 beskriver poolingprocessen ytterligare. Inmatningen är av storleken 4×4. För 2×2 subsampling delas en 4×4 bild upp i fyra icke överlappande matriser av storleken 2×2. Vid max pooling är det högsta värdet av de fyra värdena i matrisen 2×2 utgångsvärdet. Vid average pooling är genomsnittet av de fyra värdena utgångsvärdet. Observera att för utdata med index (2,2) är resultatet av medelvärdesbildningen en bråkdel som har avrundats till närmaste heltal.

Figur 7: Pictorial representation of max pooling and average pooling

Non-lineära lager

Neurala nätverk i allmänhet och CNN:s i synnerhet förlitar sig på en icke-linjär ”trigger”-funktion för att signalera distinkt identifiering av sannolika funktioner på varje dolt lager. CNN:er kan använda en mängd olika specifika funktioner – t.ex. rektifierade linjära enheter (ReLU) och kontinuerliga utlösande (icke-linjära) funktioner – för att effektivt implementera denna icke-linjära utlösande funktion.

ReLU

En ReLU implementerar funktionen y = max(x,0), så ingångs- och utgångsstorlekarna för detta skikt är desamma. Det ökar de icke-linjära egenskaperna hos beslutsfunktionen och det övergripande nätverket utan att påverka de receptiva fälten hos konvolutionslagret. Jämfört med andra icke-linjära funktioner som används i CNN (t.ex. hyperbolisk tangent, absolut hyperbolisk tangent och sigmoid) är fördelen med ReLU att nätverket tränas många gånger snabbare. ReLU-funktionen illustreras i figur 8, med dess överföringsfunktion plottad ovanför pilen.

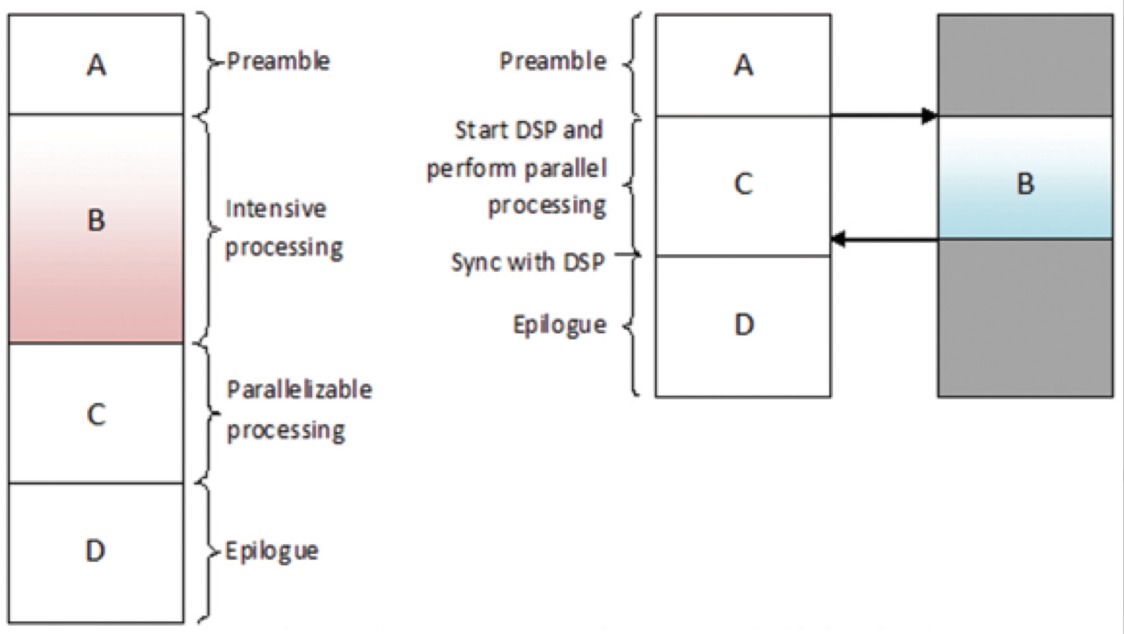
Figur 8: Bildlig representation av ReLU-funktionen

Kontinuerlig utlösande (icke-linjär) funktion

Det icke-linjära skiktet arbetar element för element i varje funktion. En kontinuerlig utlösande funktion kan vara hyperbolisk tangent (figur 9), absolut av hyperbolisk tangent (figur 10) eller sigmoid (figur 11). Figur 12 visar hur icke-linjäritet tillämpas element för element.

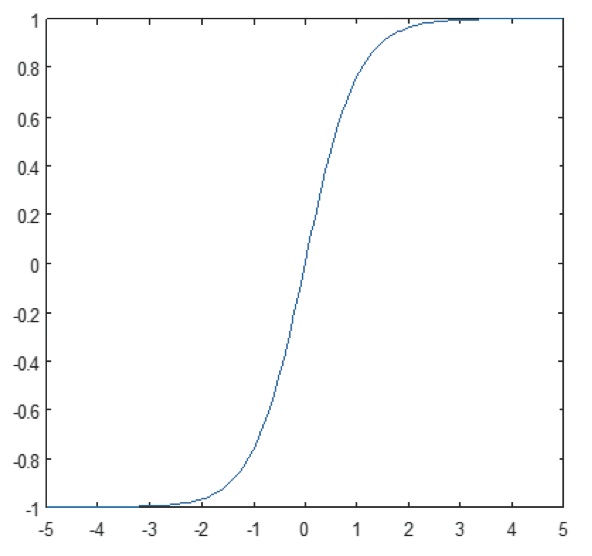
Figur 9: Plot av hyperbolisk tangentfunktion

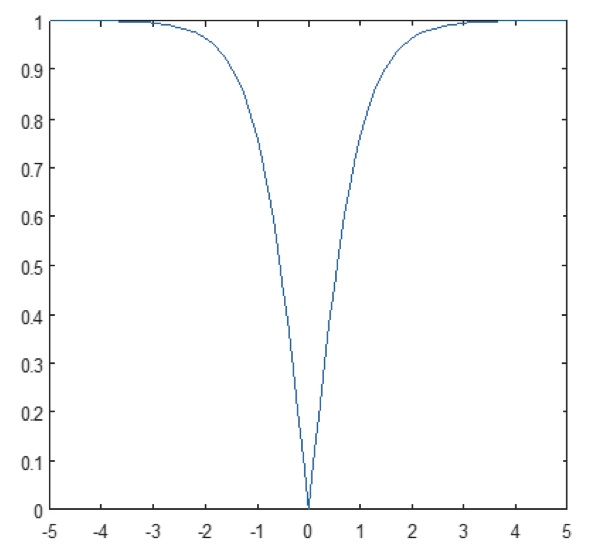
Figur 10: Plot av absolut av hyperbolisk tangentfunktion

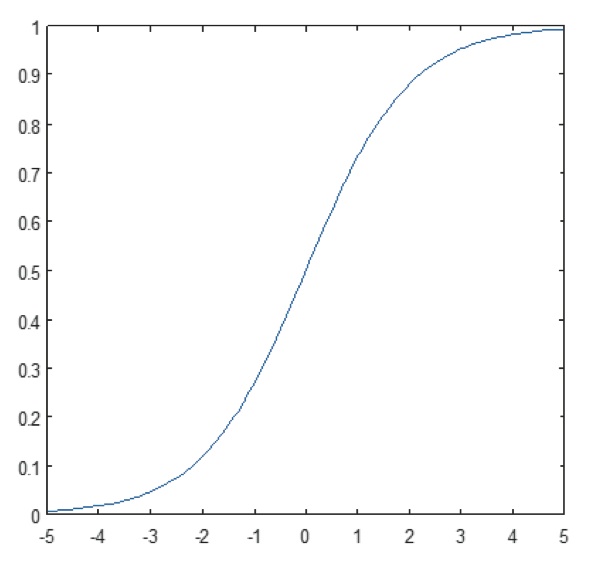
Figur 11: Plot av sigmoidfunktion

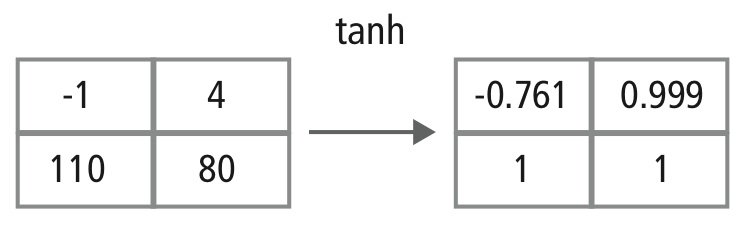
Figur 12: Bildlig representation av tanh-bearbetning

Fullt anslutna lager

Fullt anslutna lager används ofta som de sista lagren i en CNN. Dessa lager summerar matematiskt en viktning av det föregående lagrets funktioner, vilket anger den exakta blandningen av ”ingredienser” för att bestämma ett specifikt målresultat. När det gäller ett fullt sammankopplat lager används alla element från alla funktioner i det föregående lagret vid beräkningen av varje element i varje utgångsfunktion.

Figur 13 förklarar det fullt sammankopplade lagret L. Lager L-1 har två funktioner, som var och en är 2×2, dvs. har fyra element. Lager L har två funktioner som var och en har ett enda element.

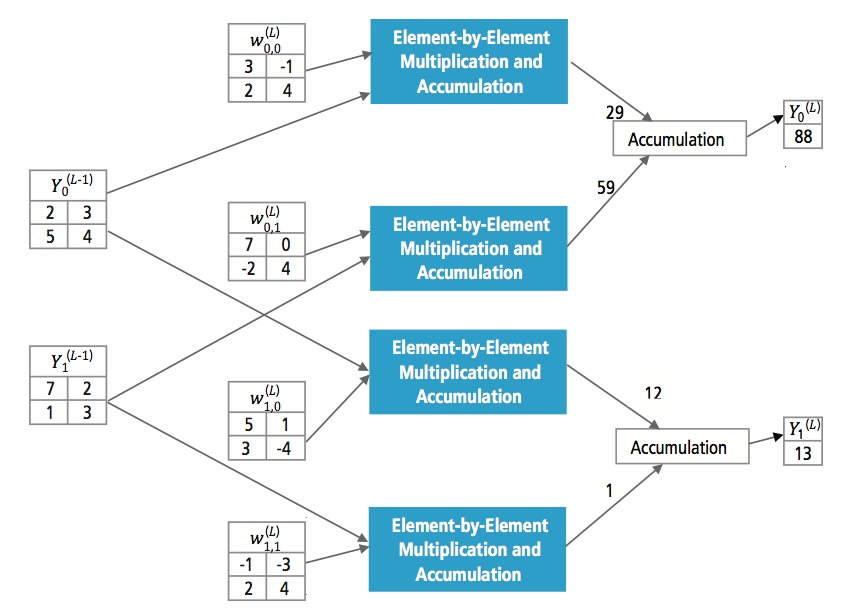
Figur 13: Bearbetning av ett fullt anslutet lager

Varför CNN?

Men även om neurala nätverk och andra metoder för mönsterdetektering har funnits under de senaste 50 åren har det skett en betydande utveckling inom området för konvolutionella neurala nätverk under senare tid. I det här avsnittet behandlas fördelarna med att använda CNN för bildigenkänning.

Ruggighet mot förskjutningar och förvrängningar i bilden

Detektering med hjälp av CNN är robust mot förvrängningar, t.ex. formförändringar på grund av kameralinsen, olika belysningsförhållanden, olika poser, förekomst av partiell ocklusion, horisontella och vertikala förskjutningar osv. CNN:er är dock oföränderliga eftersom samma viktkonfiguration används i hela rummet. Teoretiskt sett kan vi också uppnå skiftinvarians genom att använda fullt anslutna lager. Men resultatet av träningen blir i detta fall flera enheter med identiska viktmönster på olika ställen i inmatningen. För att lära sig dessa viktkonfigurationer skulle det krävas ett stort antal träningsinstanser för att täcka utrymmet av möjliga variationer.

Mindre minneskrav

I samma hypotetiska fall där vi använder ett fullt anslutet lager för att extrahera funktionerna, kommer en inmatningsbild i storleken 32×32 och ett dolt lager med 1 000 funktioner att kräva en storleksordning på 106 koefficienter, vilket är ett enormt minneskrav. I det konvolutionella lagret används samma koefficienter på olika platser i utrymmet, så minneskravet minskar drastiskt.

Enklare och bättre träning

Och om man använder det vanliga neurala nätverket som skulle motsvara ett CNN, eftersom antalet param- etrar skulle vara mycket högre, skulle träningstiden också öka proportionerligt. I ett CNN, eftersom antalet parametrar är drastiskt reducerat, minskar utbildningstiden proportionellt. Om vi antar att träningen är perfekt kan vi också konstruera ett standardneuralt nätverk vars prestanda skulle vara densamma som ett CNN. Men vid praktisk träning skulle
ett neuralt standardnätverk som motsvarar CNN ha fler parametrar, vilket skulle leda till att mer brus läggs till under träningsprocessen. Därför kommer prestandan hos ett neuralt standardnätverk som är likvärdigt med ett CNN alltid att vara sämre.

Algoritm för igenkänning av GTSRB-dataset

The German Traffic Sign Recognition Benchmark (GTSRB) var en utmaning för klassificering av flera klasser och en enda bild som hölls vid International Joint Conference on Neural Networks (IJCNN) 2011, med följande krav:

• 51 840 bilder av tyska vägskyltar i 43 klasser (figur 14 och 15)
• Bildernas storlek varierar från 15×15 till 222×193
• Bilderna är grupperade per klass och spår med minst 30 bilder per spår
• Bilderna finns tillgängliga som färgbilder (RGB), HOG-funktioner, Haar-funktioner och färghistogram
• Tävlingen gäller endast klassificeringsalgoritmen; Algoritm för att hitta intressanta områden i bilden krävs inte
• Temporal information för testsekvenserna delas inte, så den temporala dimensionen kan inte användas i klassificeringsalgoritmen

Figur 14: GTSRB idealiska trafikskyltar

Figur 15: GTSRB trafikskyltar med försämringar

Cadence algoritm för igenkänning av trafikskyltar i GTSRB-dataset

Cadence har utvecklat olika algoritmer i MATLAB för igenkänning av trafikskyltar med hjälp av GTSRB-datasetet, och har börjat med en grundkonfiguration som bygger på en välkänd artikel om igenkänning av skyltar . Den korrekta upptäcktsfrekvensen på 99,24 % och beräkningsinsatsen på nästan >50 miljoner multiplicerade adderingar per skylt visas som en tjock grön punkt i figur 16. Cadence har uppnått betydligt bättre resultat med hjälp av vår nya egenutvecklade hierarkiska CNN-metod. I denna algoritm har 43 trafikskyltar delats in i fem familjer. Totalt implementerar vi sex mindre CNN:er. Den första CNN:n avgör vilken familj den mottagna trafikskylten tillhör. När skyltens familj är känd körs den CNN (en av de återstående fem) som motsvarar den upptäckta familjen för att avgöra vilken trafikskylt som ingår i den familjen. Med hjälp av denna algoritm har Cadence uppnått en korrekt detektionsgrad på 99,58 %, vilket är den bästa CDR som hittills uppnåtts på GTSRB.

Algoritm för avvägning mellan prestanda och komplexitet

För att kontrollera komplexiteten hos CNN:er i inbäddade tillämpningar har Cadence också utvecklat en egenutvecklad algoritm med hjälp av egenvärdedekomposition som reducerar en tränad CNN till sin kanoniska dimension. Med hjälp av denna algoritm har vi kunnat minska CNN:s komplexitet drastiskt utan någon försämrad prestanda, eller med en liten kontrollerad CDR-reduktion. Figur 16 visar de uppnådda resultaten:

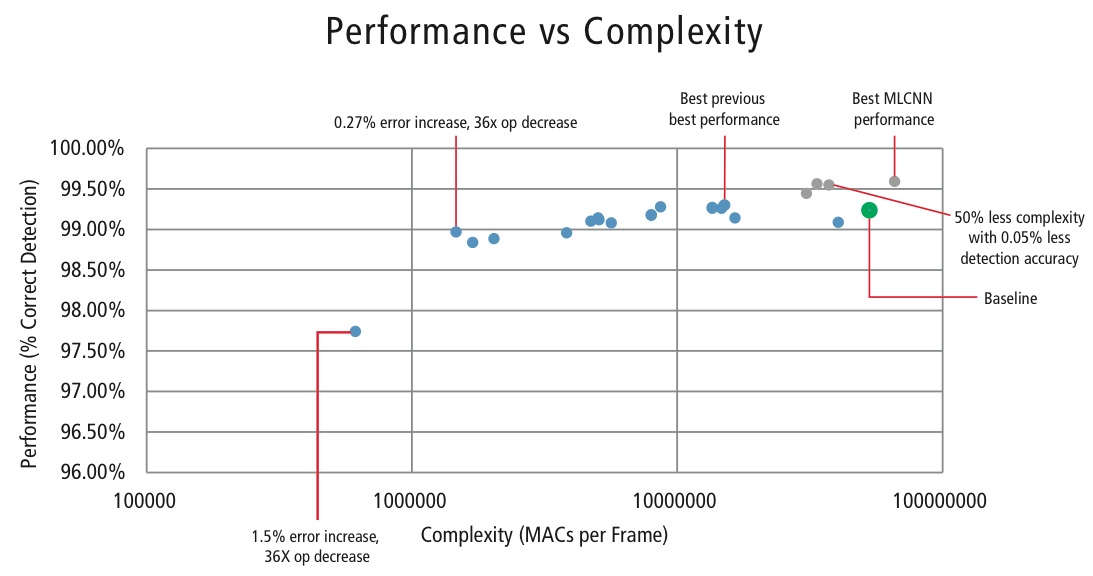
Figur 16: Diagram över prestanda kontra komplexitet för olika CNN-konfigurationer för att upptäcka trafikskyltar i GTSRB-dataset

Den gröna punkten i figur 16 är baskonfigurationen. Denna konfiguration ligger ganska nära den konfiguration som föreslås i referens . Den kräver 53 MMACs per ram för en felprocent på 0,76 %.

• Den andra punkten från vänster kräver 1,47 miljoner MACs per ram för en felprocent på 1,03 %, dvs, för en ökning av felprocenten med 0,27 % har MAC-kravet minskat med en faktor 36,14.
• Punkten längst till vänster kräver 0,61 MMACs per bild för att uppnå en felprocent på 2,26 %, dvs. antalet MACs har minskats med en faktor 86,4 gånger.
• Punkterna i blått gäller för en CNN med en enda nivå, medan punkterna i rött gäller för en hierarkisk CNN. Den hierarkiska CNN:n ger i bästa fall en prestanda på 99,58 %.

CNN:er i inbyggda system

Som framgår av figur 5 kräver ett delsystem för vision en hel del bildbehandling utöver en CNN. För att kunna köra CNN:er på ett inbäddat system med begränsad strömförsörjning som stöder bildbehandling bör det uppfylla följande krav:

• Tillgänglighet till hög beräkningsprestanda: För en typisk CNN-implementering krävs miljarder MACs per sekund.
• Större bandbredd för belastning/lagring: När det gäller ett fullt anslutet lager som används för klassificering används varje koefficient endast en gång vid multiplikation. Så kravet på bandbredd för lastning och lagring är större än antalet MACs som utförs av processorn.
• Lågt dynamiskt effektbehov: Systemet bör förbruka mindre ström. För att lösa denna fråga krävs en fastpunktsimplementering, vilket innebär att prestandakraven måste uppfyllas med minsta möjliga antal bitar.
• Flexibilitet: För att uppfylla prestandakraven måste man använda ett så litet antal bitar som möjligt: Det bör vara möjligt att enkelt uppgradera den befintliga konstruktionen till en ny konstruktion med bättre prestanda.

Med tanke på att beräkningsresurser alltid är en begränsning i inbäddade system, om användningsfallet tillåter en liten försämring av prestandan, är det bra att ha en algoritm som kan uppnå enorma besparingar i beräkningskomplexitet på bekostnad av en kontrollerad liten försämring av prestandan. Så Cadences arbete med en algoritm för att uppnå en kompromiss mellan komplexitet och prestanda, som förklaras i föregående avsnitt, har stor relevans för implementering av CNN:er i inbyggda system.

CNN:er på Tensilica-processorer

Tensilica Vision P5 DSP är en högpresterande DSP med låg effekt som är särskilt utformad för bild- och datorsynsbehandling. DSP:n har en VLIW-arkitektur med SIMD-stöd. Den har fem emissionslägen i ett instruktionsord på upp till 96 bitar och kan ladda upp till 1024-bitars ord från minnet varje cykel. Interna register och operationsenheter sträcker sig från 512 bitar till 1536 bitar, där data representeras som 16, 32 eller 64 skivor av 8b, 16b, 24b, 32b eller 48b pixeldata.

DSP:n tar itu med alla utmaningar för att implementera CNN:er i inbäddade system som diskuterades i föregående avsnitt.

• Tillgänglighet till hög beräkningsprestanda: Förutom det avancerade stödet för genomförande av bildsignalbehandling har DSP:n instruktionsstöd för alla CNN-steg. För konvolutionsoperationer har den en mycket rik instruktionsuppsättning med stöd för multiplicera/multiplicera-ackumulera-operationer med stöd för 8b x 8b, 8b x 16b och 16b x 16b operationer för signerade/icke-signerade data. Den kan utföra upp till 64 8b x 16b och 8b x 8b multiplicera/multiplicera-ackumulera operationer i en cykel och 32 16b x 16b multiplicera/multiplicera-ackumulera operationer i en cykel. För maximal pooling och ReLU-funktionalitet har DSP:n instruktioner för att göra 64 8-bitars jämförelser i en cykel. För att genomföra icke-linjära funktioner med ändliga intervall, t.ex. tanh och signum, finns det instruktioner för att genomföra en uppslagstabell för 64 7-bitarsvärden i en cykel. I de flesta fall schemaläggs instruktionerna för jämförelse och uppslagstabell parallellt med instruktionerna för multiplikation/multiplikation/ackumulering och tar inte några extra cykler i anspråk.
• Större bandbredd för lastning/lagring: DSP:n kan utföra upp till två 512-bitars lastnings-/lagringsoperationer per cykel.
• Lågt dynamiskt effektbehov: DSP är en fastpunktsmaskin. På grund av den flexibla hanteringen av en mängd olika datatyper kan full prestanda och energifördel för blandade 16b- och 8b-beräkningar uppnås med minimal förlust av noggrannhet.
• Flexibilitet: Eftersom DSP:n är en programmerbar processor kan systemet uppgraderas till en ny version bara genom att utföra en uppgradering av den fasta programvaran.
• Floating Point: För algoritmer som kräver ett utökat dynamiskt område för sina data och/eller koefficienter har DSP:n en valfri vektor-flytandepunktsenhet.

Vision P5 DSP:n levereras med en komplett uppsättning programvaruverktyg som inkluderar en högpresterande C/C++-kompilator med automatisk vektorisering och schemaläggning för att stödja SIMD- och VLIW-arkitekturen utan att behöva skriva assemblerspråk. Den här omfattande verktygslådan innehåller också länkar, assembler, debugger, profilerare och grafiska visualiseringsverktyg. En omfattande instruktionsuppsättningssimulator (ISS) gör det möjligt för konstruktören att snabbt simulera och utvärdera prestanda. När man arbetar med stora system eller långa testvektorer uppnår det snabba, funktionella simulatoralternativet TurboXim hastigheter som är 40X till 80X snabbare än ISS för effektiv mjukvaruutveckling och funktionell verifiering.

Cadence har implementerat en CNN-arkitektur med ett enda lager på DSP:en för tysk trafikskyltigenkänning. Cadence har uppnått en CDR på 99,403 % med 16-bitars kvantisering för dataprover och 8-bitars kvantisering för koefficienter i alla lager för denna arkitektur. Den har två konvolutionslager, tre fullt anslutna lager, fyra ReLU-lager, tre max pooling-lager och ett tanh icke-linjärt lager. Cadence har uppnått en genomsnittlig prestanda på 38,58 MACs/cykel för hela nätverket, inklusive cyklerna för alla max pooling-, tanh- och ReLU-skikt. Cadence har i bästa fall uppnått en prestanda på 58,43 MAC per cykel för det tredje lagret, inklusive cyklerna för tanh- och ReLU-funktionerna. Denna DSP som körs på 600 MHz kan bearbeta mer än 850 trafikskyltar på en sekund.

Framtiden för CNN

En av de lovande områdena inom forskningen om neurala nätverk är återkommande neurala nätverk (RNN) som använder sig av långa korttidsminnen (LSTM). Dessa områden ger det nuvarande tekniska utvecklingsläget när det gäller tidsserierekognition, t.ex. taligenkänning och handskriftsigenkänning. RNN/autoenkoder kan också generera handskrift/tal/bilder med en viss känd fördelning ,,,,.

Deep belief networks, en annan lovande typ av nätverk som använder restricted Boltzman machines (RMBs)/autoenkoder, kan tränas girigt, ett lager i taget, och kan därför lättare tränas för mycket djupa nätverk ,.

Slutsats

CNNs ger de bästa resultaten vid problem med mönster-/bildigenkänning och överträffar till och med människor i vissa fall. Cadence har uppnått de bästa resultaten i branschen genom att använda egna algoritmer och arkitekturer med CNNs. Vi har utvecklat hierarkiska CNNs för att känna igen trafikskyltar i GTSRB och har uppnått den bästa prestandan någonsin på denna datamängd. Vi har utvecklat en annan algoritm för avvägningen mellan prestanda och komplexitet och har lyckats uppnå en minskning av komplexiteten med en faktor 86 för en försämring av CDR på mindre än 2 %. Tensilica Vision P5 DSP för bildbehandling och datorseende från Cadence har alla de funktioner som krävs för att implementera CNN:er utöver de funktioner som krävs för bildsignalbehandling. Mer än 850 igenkänningar av trafikskyltar kan utföras när DSP:n körs på 600 MHz. Tensilica Vision P5 DSP från Cadence har en nästan idealisk uppsättning funktioner för att köra CNNs.

”Artificial neural network”. Wikipedia. https://en.wikipedia.org/wiki/Artificial_neural_network

Karpathy, Andrej. 2015. ”Neurala nätverk, del 1: Upprättande av arkitekturen”. Notes for CS231n Convolutional Neural Networks for Visual Recognition, Stanford University. http://cs231n.github.io/neural-networks-1/

”Convolutional neural network”. Wikipedia. https://en.wikipedia.org/wiki/Convolutional_neural_network

Sermanet, Pierre och Yann LeCun. 2011. ”Traffic Sign Recognition with Multi Scale Networks”. Courant Institute of Mathematical Sciences, New York University. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6033589

Ciresan, Dan, Ueli Meier och Jürgen Schmidhuber. 2012. ”Multi-column deep neural networks for image classi- fication”. 2012 IEEE Conference on Computer Vision and Pattern Recognition (New York, NY: Institute of Electrical and Electronics Engineers (IEEE)). http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6248110

Ciresan, Dan, Ueli Meier, Jonathan Masci, Luca M. Gambardella och Jurgen Schmidhuber. 2011. ”Flexibla, högpresterande konvolutionella neurala nätverk för bildklassificering”. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence-Volume Two: 1237-1242. Hämtad den 17 november 2013. http://people.idsia.ch/~juergen/ijcai2011.pdf

Lawrence, Steve, C. Lee Giles, Ah Chung Tsoi och Andrew D. Back. 1997. ”Face Recognition (ansiktsigenkänning): A Convolutional Neural Network Approach. IEEE Transactions on Neural Networks, volym 8, nummer 1. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=554195

Russakovsky, O. et al. 2014. ”ImageNet Large Scale Visual Recognition Challenge”. International Journal of Computer Vision. http://link.springer.com/article/10.1007/s11263-015-0816-y#

Ovtcharov, Kalin, Olatunji Ruwarse, Joo-Young Kim et al. 22 februari 2015. ”Accelerating Deep Convolutional Networks Using Specialized Hardware”. Microsoft Research. http://research-srv.microsoft.com/pubs/240715/CNN%20Whitepaper.pdf

Stallkamp, J., M. Schlipsing, J. Salmen och C. Igel. ”Man Vs. Computer: Benchmarking Machine Learning Algorithms For Traffic Sign Application”. IJCNN 2011. http://www.sciencedirect.com/science/article/pii/S0893608012000457

Hochreiter, Sepp och Jürgen Schmidhuber. 1997. ”Long Short-Term Memory”. Neural Computation, 9(8):1735-1780. ftp://ftp.idsia.ch/pub/juergen/lstm.pdf

Graves, Alex. 2014. ”Generating Sequences With Recurrent Neural Networks”. http://arxiv.org/abs/1308.0850

Schmidhuber, Jurgen. 2015. ”Recurrent Neural Networks.” http://people.idsia.ch/~juergen/rnn.html

Olshausen, Bruno A. och David J. Field. 1996. ”Emergence of simple-cell receptive field properties by learning a sparse code for natural images”. Nature 381.6583: 607-609. http://www.nature.com/nature/journal/v381/n6583/abs/381607a0.html

Hinton, G. E. och Salakhutdinov, R. R. 2006. ”Reducing the dimensionality of data with neural networks”. Science vol. 313 no. 5786 pp. 504-507. http://www.sciencemag.org/content/suppl/2006/08/04/313.5786.504.DC1.

Hinton, Geoffrey E. 2009. ”Deep belief networks”. Scholarpedia, 4(5):5947.
http://www.scholarpedia.org/article/Deep_belief_networks