De-Multiplexer er et kombinationskredsløb, der udfører den omvendte operation af Multiplexer. Det har en enkelt indgang, “n” valglinjer og højst 2n udgange. Indgangen forbindes med en af disse udgange på grundlag af værdierne på valglinjerne.

Da der er “n” valglinjer, vil der være 2n mulige kombinationer af nuller og ettaller. Så hver kombination kan kun vælge én udgang. De-Multiplexer kaldes også De-Mux.

1×4 De-Multiplexer

1×4 De-Multiplexer har én indgang I, to valglinjer, s1 & s0 og fire udgange Y3, Y2, Y1 &Y0. Blokdiagrammet for 1×4 De-Multiplexer er vist i følgende figur.

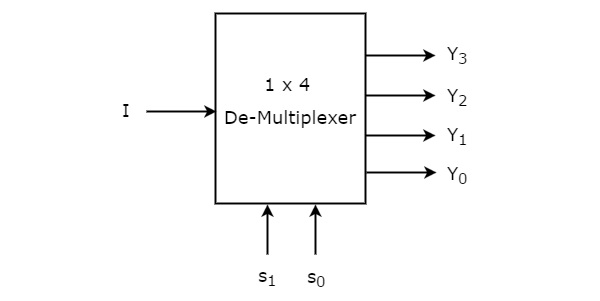
Den enkelte indgang “I” vil blive forbundet til en af de fire udgange, Y3 til Y0, baseret på værdierne af valglinjerne s1 & s0. Sandhedstabellen for 1×4 De-Multiplexer er vist nedenfor.

Selektionsindgange		Udgange
S1	S0	Y3	Y3	Y2	Y1	Y0
0	0	0	0	0	0	I
0	1	0	0	I	0
1	0	0	0	I	0	0	0
1	1	I	0	0	0	0

Fra ovenstående sandhedstabel, kan vi direkte skrive de boolske funktioner for hvert output som

$$$Y_{3}=s_{1}s_{0}I$$$

$$$Y_{2}=s_{1}{s_{0}}}’I$$$

$$$Y_{1}={s_{1}}}’s_{0}}I$$$

$$$Y_{0}={s_1}'{s_{0}}}’I$$

Vi kan implementere disse boolske funktioner ved hjælp af invertere & 3-input AND gates. Kredsløbsdiagrammet for 1×4 De-Multiplexer er vist i følgende figur.

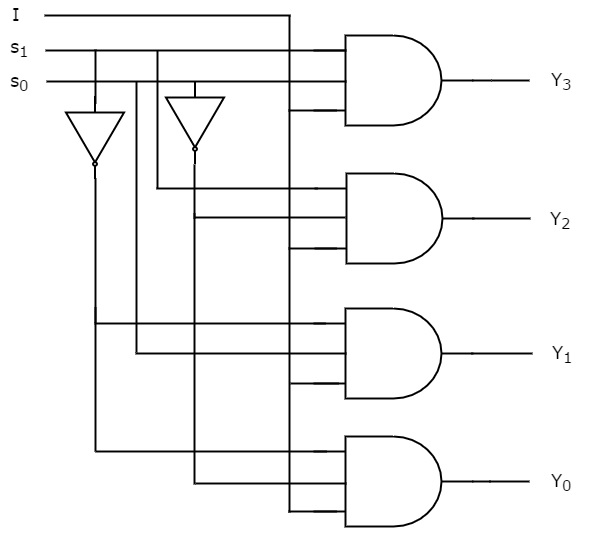
Vi kan let forstå driften af ovenstående kredsløb. På samme måde kan du implementere 1×8 De-Multiplexer og 1×16 De-Multiplexer ved at følge den samme procedure.

Implementering af højere ordens De-Multiplexere

Nu skal vi implementere følgende to højere ordens De-Multiplexere ved hjælp af lavere ordens De-Multiplexere.

• 1×8 De-Multiplexer
• 1×16 De-Multiplexer

1×8 De-Multiplexer

I dette afsnit skal vi implementere 1×8 De-Multiplexer ved hjælp af 1×4 De-Multiplexer og 1×2 De-Multiplexer. Vi ved, at 1×4 De-Multiplexer har en enkelt indgang, to valglinjer og fire udgange. Mens 1×8 De-Multiplexer har en enkelt indgang, tre udvælgelseslinjer og otte udgange.

Så vi har brug for to 1×4 De-Multiplexere i andet trin for at få de endelige otte udgange. Da antallet af indgange i andet trin er to, har vi brug for en 1×2 DeMultiplexer i første trin, så udgangene fra første trin bliver indgangene i andet trin. Indgangen fra denne 1×2 De-Multiplexer vil være den samlede indgang til 1×8 De-Multiplexer.

Lad 1×8 De-Multiplexeren have en indgang I, tre valglinjer s2, s1 & s0 og udgangene Y7 til Y0. Sandhedstabellen for 1×8 De-Multiplexeren er vist nedenfor.

Selektionsindgange			Udgange
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0	0

Vi kan gennemføre 1×8 De-Multiplexer ved hjælp af multiplexere af lavere orden nemt ved at tage ovenstående sandhedstabel i betragtning. Blokdiagrammet for 1×8 De-Multiplexeren er vist i følgende figur.

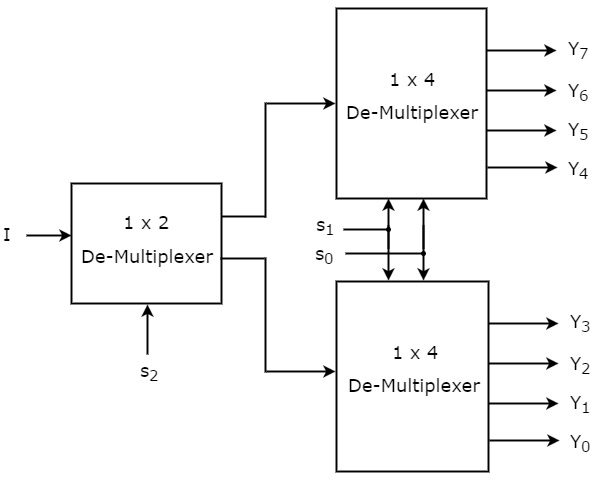
De fælles valglinjer, s1 & s0 anvendes på begge 1×4 De-Multiplexere. Udgangene fra den øverste 1×4 De-Multiplexer er Y7 til Y4 og udgangene fra den nederste 1×4 De-Multiplexer er Y3 til Y0.

Den anden valglinje, s2, anvendes til 1×2 De-Multiplexer. Hvis s2 er nul, vil en af de fire udgange i den nederste 1×4 De-Multiplexer være lig med input, I baseret på værdierne af valglinjerne s1 & s0. Tilsvarende, hvis s2 er et, vil en af de fire udgange af den øverste 1×4 DeMultiplexer være lig med input, I baseret på værdierne af valglinjerne s1 & s0.

1×16 De-Multiplexer

I dette afsnit skal vi implementere 1×16 De-Multiplexer ved hjælp af 1×8 De-Multiplexere og 1×2 De-Multiplexer. Vi ved, at 1×8 De-Multiplexer har en enkelt indgang, tre valglinjer og otte udgange. Mens 1×16 De-Multiplexer har en enkelt indgang, fire valglinjer og seksten udgange.

Så vi har brug for to 1×8 De-Multiplexere i andet trin for at få de endelige seksten udgange. Da antallet af indgange i andet trin er to, skal vi bruge 1×2 DeMultiplexer i første trin, således at udgangene fra første trin bliver indgangene i andet trin. Indgangen fra denne 1×2 De-Multiplexer vil være den samlede indgang til 1×16 De-Multiplexer.

Lad 1×16 De-Multiplexeren have en indgang I, fire valglinjer s3, s2, s1 & s0 og udgange Y15 til Y0. Blokdiagrammet for 1×16 De-Multiplexer ved hjælp af multiplexere af lavere orden er vist i følgende figur.

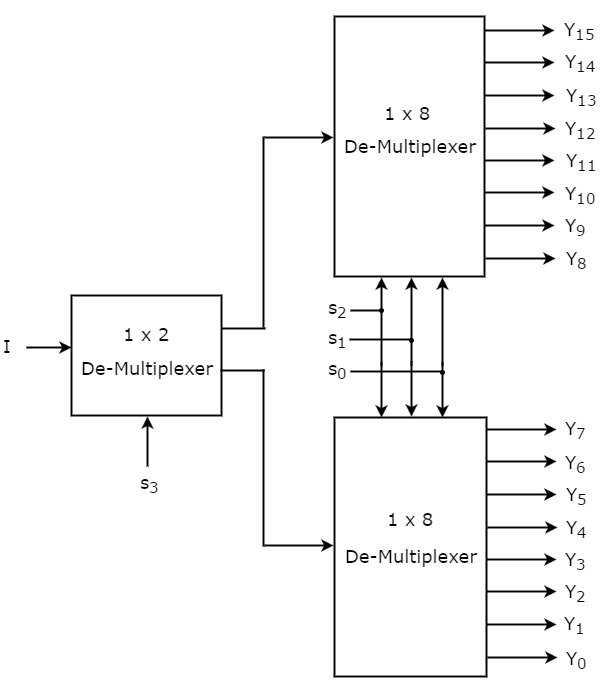
De fælles udvælgelseslinjer s2, s1 & s0 anvendes til begge 1×8 De-Multiplexere. Udgangene fra den øverste 1×8 De-Multiplexer er Y15 til Y8 og udgangene fra den nederste 1×8 DeMultiplexer er Y7 til Y0.

Den anden valglinje, s3, anvendes til 1×2 De-Multiplexeren. Hvis s3 er nul, vil en af de otte udgange i den nederste 1×8 De-Multiplexer være lig med input, I baseret på værdierne af valglinjerne s2, s1 & s0. Tilsvarende, hvis s3 er et, vil en af de otte udgange i den øverste 1×8 De-Multiplexer være lig med input, I baseret på værdierne af valglinjerne s2, s1 & s0.