Tento článek byl původně publikován na webových stránkách společnosti Cadence. Zde je přetištěn se souhlasem společnosti Cadence.

Konvoluční neuronové sítě (CNN) jsou široce používány v problémech rozpoznávání vzorů a obrazů, protože mají ve srovnání s jinými technikami řadu výhod. Tato bílá kniha se zabývá základy CNN včetně popisu jednotlivých používaných vrstev. Na příkladu rozpoznávání dopravních značek diskutujeme o výzvách tohoto obecného problému a představujeme algoritmy a implementační software vyvinutý společností Cadence, který dokáže vyměnit výpočetní zátěž a energii za mírné zhoršení míry rozpoznávání značek. Nastíníme výzvy spojené s použitím CNN ve vestavěných systémech a představíme klíčové vlastnosti digitálního signálového procesoru (DSP) Cadence® Tensilica® Vision P5 pro zobrazování a počítačové vidění a softwaru, díky nimž je tak vhodný pro aplikace CNN v mnoha zobrazovacích a souvisejících rozpoznávacích úlohách.

Co je CNN?

Nervová síť je systém vzájemně propojených umělých „neuronů“, které si mezi sebou vyměňují zprávy. Spojení mají číselné váhy, které jsou během procesu trénování vyladěny tak, aby správně natrénovaná síť správně reagovala, když je jí předložen obraz nebo vzor k rozpoznání. Síť se skládá z několika vrstev „neuronů“ detekujících příznaky. Každá vrstva má mnoho neuronů, které reagují na různé kombinace vstupů z předchozích vrstev. Jak ukazuje obrázek 1, vrstvy jsou sestaveny tak, že první vrstva detekuje sadu primitivních vzorů na vstupu, druhá vrstva detekuje vzory vzorů, třetí vrstva detekuje vzory těchto vzorů atd. Typické CNN používají 5 až 25 různých vrstev pro rozpoznávání vzorů.

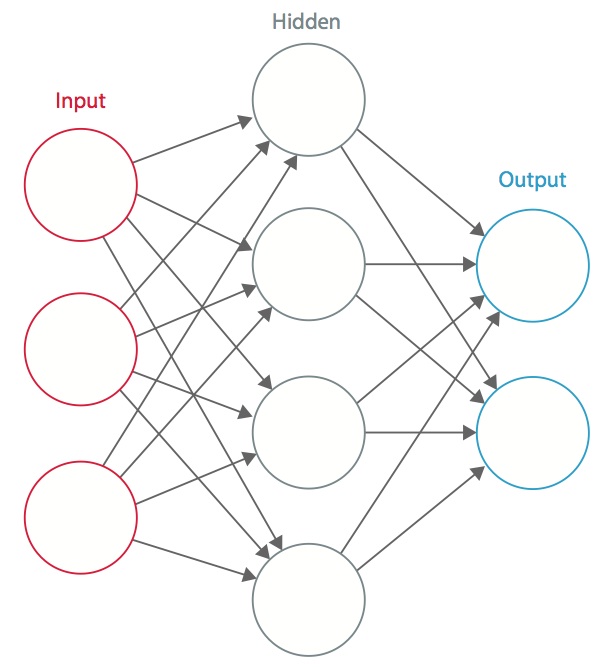
Obrázek 1: Umělá neuronová síť

Trénování se provádí pomocí „označené“ sady vstupních dat v širokém sortimentu reprezentativních vstupních vzorů, které jsou označeny jejich zamýšlenou výstupní odezvou. Při trénování se používají metody pro obecné použití, které iterativně určují váhy pro mezilehlé a konečné funkční neurony. Obrázek 2 ukazuje proces trénování na úrovni bloků.

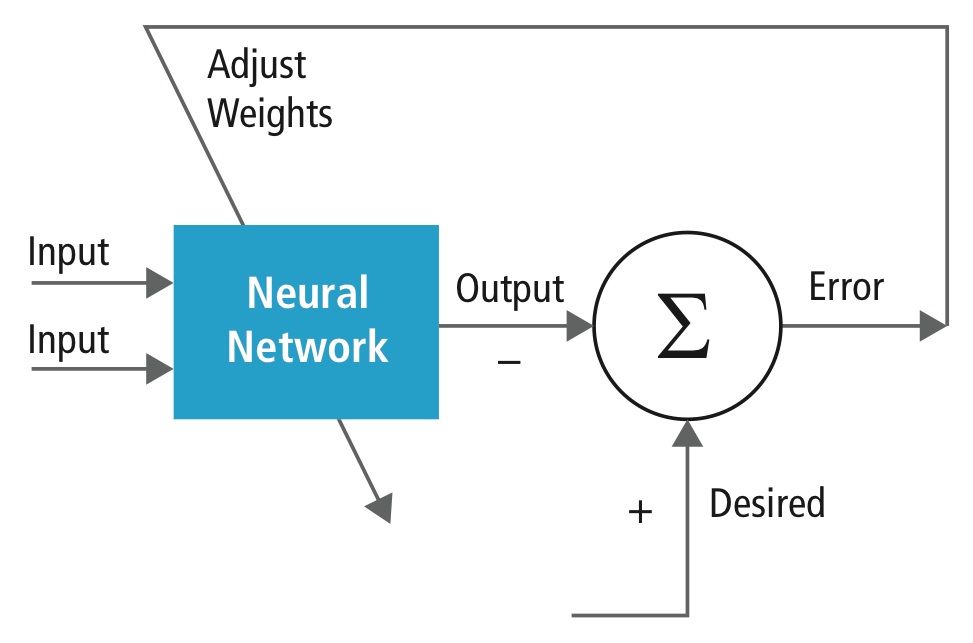
Obrázek 2: Trénování neuronových sítí

Neuronové sítě jsou inspirovány biologickými neuronovými systémy. Základní výpočetní jednotkou mozku je neuron a ty jsou propojeny synapsemi. Obrázek 3 porovnává biologický neuron se základním matematickým modelem .

Obrázek 3: Ilustrace biologického neuronu (nahoře) a jeho matematického modelu (dole)

V reálném živočišném neuronovém systému je neuron vnímán tak, že přijímá vstupní signály ze svých dendritů a produkuje výstupní signály po svém axonu. Axon se větví a prostřednictvím synapsí se připojuje k dendritům jiných neuronů. Když kombinace vstupních signálů dosáhne určité prahové podmínky mezi jeho vstupními dendrity, neuron je aktivován a jeho aktivace je sdělena nástupnickým neuronům.

Ve výpočetním modelu neuronové sítě signály, které putují podél axonů (např. x0), interagují multiplicitně (např. w0x0) s dendrity jiného neuronu na základě synaptické síly na dané synapsy (např. w0). Synaptické váhy se dají naučit a řídí vliv jednoho nebo druhého neuronu. Dendrity přenášejí signál do těla buňky, kde se všechny sečtou. Pokud je konečný součet vyšší než určitý práh, neuron vystřelí a vyšle po svém axonu hrot. Ve výpočetním modelu se předpokládá, že na přesném načasování vypálení nezáleží a informaci sděluje pouze frekvence vypálení. Na základě interpretace rychlostního kódu je rychlost vypalování neuronu modelována aktivační funkcí ƒ, která představuje frekvenci výboje podél axonu. Běžnou volbou aktivační funkce je sigmoida. Stručně řečeno, každý neuron vypočítá bodový součin vstupů a vah, přičte zkreslení a použije nelinearitu jako aktivační funkci (například podle sigmoidní funkce odezvy).

Koncentrovaná síť je speciálním případem výše popsané neuronové sítě. CNN se skládá z jedné nebo více konvolučních vrstev, často se subsamplovací vrstvou, za nimiž následuje jedna nebo více plně propojených vrstev jako ve standardní neuronové síti.

Návrh CNN je motivován objevem vizuálního mechanismu, zrakové kůry, v mozku. Zraková kůra obsahuje množství buněk, které jsou zodpovědné za detekci světla v malých, překrývajících se podoblastech zorného pole, které se nazývají receptivní pole. Tyto buňky fungují jako lokální filtry nad vstupním prostorem a složitější buňky mají větší receptivní pole. Konvoluční vrstva v CNN vykonává funkci, kterou vykonávají buňky ve zrakové kůře .

Typická CNN pro rozpoznávání dopravních značek je znázorněna na obrázku 4. Každá funkce vrstvy přijímá vstupy ze sady funkcí nacházejících se v malém okolí v předchozí vrstvě, které se nazývá lokální receptivní pole. Pomocí lokálních receptivních polí mohou funkce extrahovat elementární vizuální rysy, jako jsou orientované hrany, koncové body, rohy atd. a ty jsou pak kombinovány vyššími vrstvami.

V tradičním modelu rozpoznávání vzorů/obrazů shromažďuje ručně navržený extraktor rysů relevantní infor- mace ze vstupu a eliminuje irelevantní proměnné. Po extraktoru následuje trénovatelný klasifikátor, standardní neuronová síť, která klasifikuje vektory příznaků do tříd.

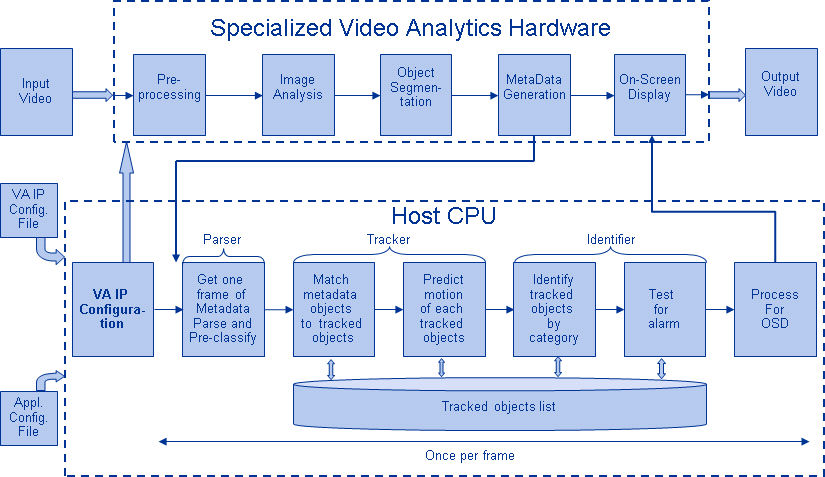
V CNN hrají roli extraktoru příznaků konvoluční vrstvy. Nejsou však navrženy ručně. O vahách jádra konvolučního filtru se rozhoduje v rámci procesu trénování. Konvoluční vrstvy jsou schopny extrahovat lokální rysy, protože omezují receptivní pole skrytých vrstev na lokální.

Obrázek 4: Typické blokové schéma CNN

CNN se používají v různých oblastech, včetně rozpoznávání obrazu a vzorů, rozpoznávání řeči, zpracování přirozeného jazyka a analýzy videa. Existuje řada důvodů, proč konvoluční neuronové sítě nabývají na významu. V tradičních modelech pro rozpoznávání vzorů jsou extraktory příznaků navrhovány ručně. V CNN jsou váhy konvoluční vrstvy používané pro extrakci příznaků i plně propojené vrstvy používané pro klasifikaci určeny během procesu učení. Vylepšená síťová struktura CNN vede k úsporám paměťových nároků a požadavků na výpočetní složitost a zároveň poskytuje lepší výkon pro aplikace, kde vstup má lokální korelaci (např. obraz a řeč).

Velké požadavky na výpočetní zdroje pro trénování a vyhodnocování CNN někdy splňují grafické procesory (GPU), DSP nebo jiné křemíkové architektury optimalizované pro vysokou propustnost a nízkou spotřebu energie při provádění idiosynkratických vzorců výpočtu CNN. Ve skutečnosti mají pokročilé procesory, jako je Tensilica Vision P5 DSP for Imaging and Computer Vision od společnosti Cadence, téměř ideální sadu výpočetních a paměťových zdrojů potřebných pro provoz CNN s vysokou účinností.

V aplikacích rozpoznávání vzorů a obrazů bylo pomocí CNN dosaženo nejlepší možné míry správné detekce (CDR). CNN například dosáhly CDR 99,77 % při použití databáze ručně psaných číslic MNIST , CDR 97,47 % u datové sady 3D objektů NORB a CDR 97,6 % u ~ 5600 obrázků s více než 10 objekty. CNN nejenže podávají nejlepší výkon ve srovnání s ostatními detekčními algoritmy, ale dokonce překonávají člověka v případech, jako je klasifikace objektů do jemných kategorií, jako je konkrétní plemeno psa nebo druh ptáka .

Obrázek 5 ukazuje typický průběh algoritmu vidění, který se skládá ze čtyř fází: předběžné zpracování obrazu, detekce oblastí zájmu (ROI), které obsahují pravděpodobné objekty, rozpoznávání objektů a rozhodování o vidění. Krok předzpracování je obvykle závislý na detailech vstupu, zejména na kamerovém systému, a často je implementován v pevně zapojené jednotce mimo subsystém vidění. Rozhodování na konci pipeline obvykle pracuje s rozpoznanými objekty – může činit složitá rozhodnutí, ale pracuje s mnohem menším množstvím dat, takže tato rozhodnutí obvykle nejsou výpočetně náročné nebo paměťově náročné problémy. Velkou výzvou jsou fáze detekce a rozpoznávání objektů, kde mají nyní CNN široký dopad.

Obrázek 5: Pipeline zrakových algoritmů

Vrstvy CNN

Skládáním více a různých vrstev v CNN se vytvářejí složité architektury pro klasifikační problémy. Nejčastěji se používají čtyři typy vrstev: konvoluční vrstvy, vrstvy se sdružováním/podvzorkováním, nelineární vrstvy a plně propojené vrstvy.

Konvoluční vrstvy

Operace konvoluce extrahuje různé vlastnosti vstupu. První konvoluční vrstva extrahuje funkce nízké úrovně, jako jsou hrany, čáry a rohy. Vrstvy vyšší úrovně extrahují rysy vyšší úrovně. Obrázek 6 znázorňuje proces 3D konvoluce používaný v CNN. Vstup má velikost N x N x D a je konvolvován s H jádry, každé o velikosti
k x k x D zvlášť. Konvoluce vstupu s jedním jádrem vytváří jednu výstupní funkci a s H jádry nezávisle na sobě vytváří H funkcí. Počínaje levým horním rohem vstupu se každé jádro posouvá zleva doprava, vždy po jednom prvku. Po dosažení pravého horního rohu se jádro přesune o jeden prvek směrem dolů a opět se jádro přesune zleva doprava, vždy o jeden prvek. Tento postup se opakuje, dokud
jádro nedosáhne pravého dolního rohu. Pro případ, kdy N = 32 a k = 5 , existuje 28 jedinečných pozic zleva doprava a 28 jedinečných pozic shora dolů, které může jádro zaujmout. V souladu s těmito pozicemi bude každý prvek ve výstupu obsahovat 28×28 (tj. (N-k+1) x (N-k+1)) prvků. Pro každou pozici jádra v procesu posuvného okna se k x k x D prvků vstupu a k x k x D prvků jádra násobí prvek po prvku a kumulují. K vytvoření jednoho prvku jedné výstupní funkce je tedy zapotřebí k x k x D operací násobení-akumulace.

Obrázek 6: Obrázkové znázornění procesu konvoluce

Vrstvy sdružování/podvzorkování

Vrstva sdružování/podvzorkování snižuje rozlišení funkcí. Díky ní jsou rysy odolné proti šumu a zkreslení. Existují dva způsoby sdružování: maximální sdružování a průměrné sdružování. V obou případech je vstup rozdělen do nepřekrývajících se dvourozměrných prostorů. Například na obrázku 4 je vrstva 2 vrstvou sdružování. Každý vstupní prvek má rozměry 28×28 a je rozdělen do 14×14 oblastí o velikosti 2×2. Pro průměrné sdružování se vypočítá průměr čtyř hodnot v oblasti. Pro max pooling se vybere maximální hodnota ze čtyř hodnot.

Obrázek 7 dále rozvádí proces poolingu. Vstup má velikost 4×4. Při podvzorkování 2×2 je obraz 4×4 rozdělen na čtyři nepřekrývající se matice o velikosti 2×2. V případě podvzorkování 2×2 je obraz 4×4 rozdělen na čtyři matice o velikosti 2×2. V případě maximálního sdružování je výstupem maximální hodnota čtyř hodnot v matici 2×2. V případě průměrného sdružování je výstupem průměr čtyř hodnot. Upozorňujeme, že v případě výstupu s indexem (2,2) je výsledkem průměrování zlomek, který byl zaokrouhlen na nejbližší celé číslo.

Obrázek 7: Obrázkové znázornění maximálního sdružování a průměrného sdružování

Nelineární vrstvy

Neuronové sítě obecně a CNN zvláště spoléhají na nelineární „spouštěcí“ funkci, která signalizuje odlišnou identifikaci pravděpodobných rysů na každé skryté vrstvě. CNN mohou používat různé specifické funkce – například rektifikované lineární jednotky (ReLU) a spojité spouštěcí (nelineární) funkce – k efektivní implementaci tohoto nelineárního spouštění.

ReLU

ReLU implementuje funkci y = max(x,0), takže velikost vstupu a výstupu této vrstvy je stejná. Zvyšuje nelineární vlastnosti rozhodovací funkce a celé sítě, aniž by ovlivnila receptivní pole konvoluční vrstvy. Ve srovnání s ostatními nelineárními funkcemi používanými v CNN (např. hyperbolický tangens, absolutní hyperbolický tangens a sigmoida) je výhodou ReLU to, že se síť trénuje mnohonásobně rychleji. Funkčnost ReLU je znázorněna na obrázku 8, přičemž její přenosová funkce je vynesena nad šipkou.

Obrázek 8: Obrázkové znázornění funkčnosti ReLU

Kontinuální spouštěcí (nelineární) funkce

Nelineární vrstva pracuje prvek po prvku v každé funkci. Spojitá spouštěcí funkce může být hyperbolický tangens (obrázek 9), absolutní hodnota hyperbolického tangens (obrázek 10) nebo sigmoida (obrázek 11). Obrázek 12 ukazuje, jak se nelinearita uplatňuje prvek po prvku.

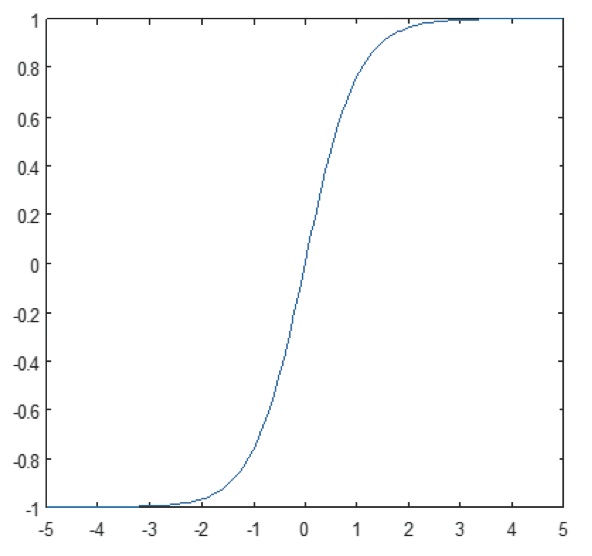
Obrázek 9: Graf hyperbolické tečné funkce

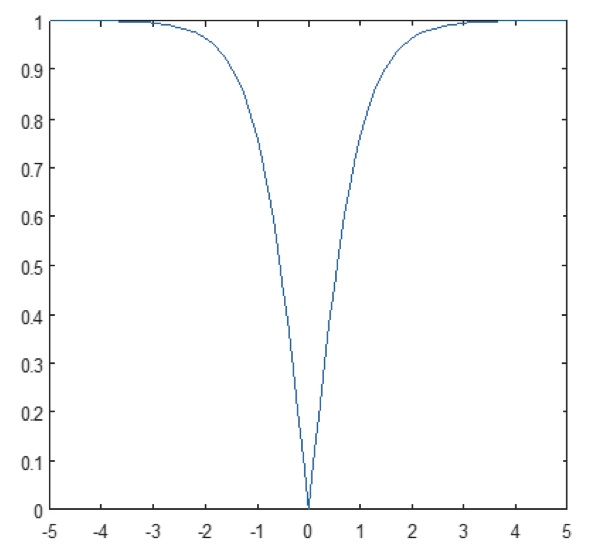
Obrázek 10: Graf absolutní hyperbolické tečné funkce

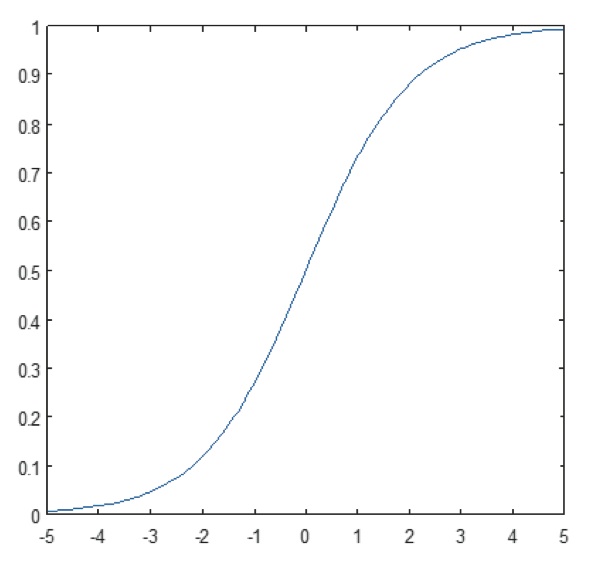
Obrázek 11: Graf sigmoidní funkce

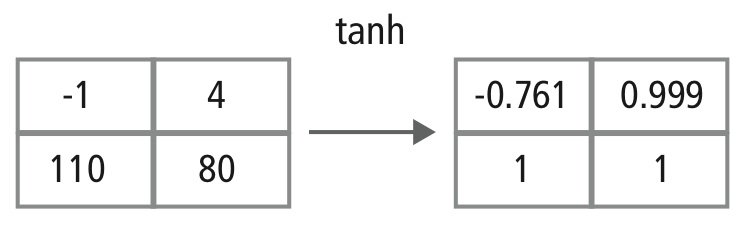
Obr. 12: Obrázkové znázornění zpracování tanh

Plně propojené vrstvy

Plně propojené vrstvy se často používají jako poslední vrstvy CNN. Tyto vrstvy matematicky sčítají váhy funkcí předchozí vrstvy a udávají přesnou kombinaci „přísad“ pro určení konkrétního cílového výstupního výsledku. V případě plně propojené vrstvy se při výpočtu každého prvku každé výstupní funkce použijí všechny prvky všech funkcí předchozí vrstvy.

Obrázek 13 vysvětluje plně propojenou vrstvu L. Vrstva L-1 má dvě funkce, z nichž každá je 2×2, tj. má čtyři prvky. Vrstva L má dvě funkce, z nichž každá má jeden prvek.

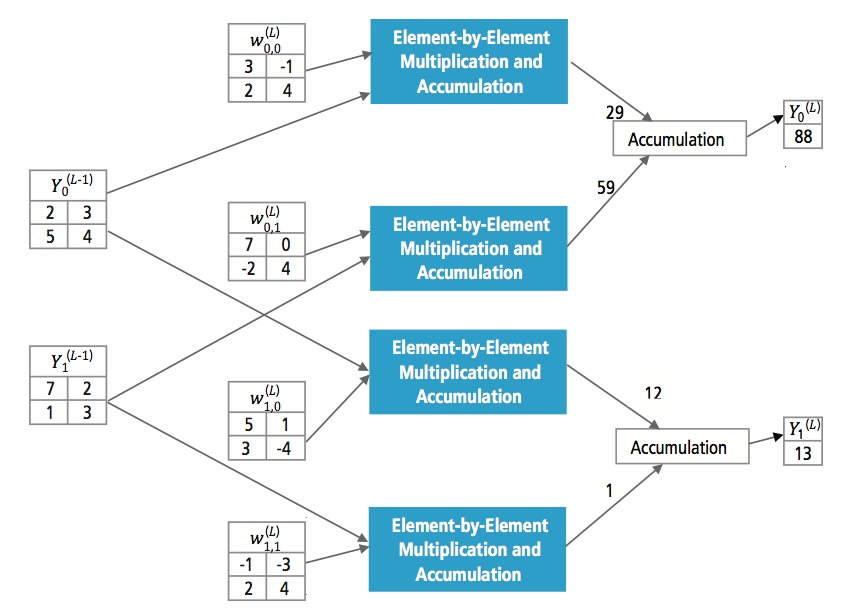
Obrázek 13: Zpracování plně propojené vrstvy

Proč CNN?

Ačkoli neuronové sítě a další metody detekce vzorů existují již 50 let, v oblasti konvolučních neuronových sítí došlo v nedávné minulosti k významnému rozvoji. Tato část se zabývá výhodami použití CNN pro rozpoznávání obrazu.

Odolnost vůči posunům a zkreslení obrazu

Detekce pomocí CNN je odolná vůči zkreslením, jako je změna tvaru způsobená objektivem fotoaparátu, různé světelné podmínky, různé pózy, přítomnost částečných zákrytů, horizontální a vertikální posuny atd. CNN jsou však posunově invariantní, protože se v celém prostoru používá stejná konfigurace vah. Teoreticky můžeme dosáhnout posunové invariantnosti také pomocí plně propojených vrstev. Výsledkem tréninku je však v tomto případě více jednotek s identickými váhovými vzorci na různých místech vstupu. K naučení těchto konfigurací vah by bylo zapotřebí velkého počtu trénovacích instancí, aby byl pokryt prostor možných variant.

Menší paměťové nároky

V tomtéž hypotetickém případě, kdy k extrakci rysů použijeme plně propojenou vrstvu, bude vstupní obraz o velikosti 32×32 a skrytá vrstva obsahující 1000 rysů vyžadovat řádově 106 koeficientů, což je obrovský paměťový požadavek. V konvoluční vrstvě se používají stejné koeficienty na různých místech v prostoru, takže paměťová náročnost se drasticky sníží.

Snadnější a lepší trénování

Při použití standardní neuronové sítě, která by odpovídala CNN, by se vzhledem k mnohem vyššímu počtu paramerů úměrně zvýšila i doba trénování. U CNN, protože počet parametrů je drasticky snížen, se doba trénování úměrně zkrátí. Také za předpokladu dokonalého trénování můžeme navrhnout standardní neuronovou síť, jejíž výkon by byl stejný jako u CNN. Ale při praktickém trénování,
standardní neuronová síť ekvivalentní CNN by měla více parametrů, což by vedlo k většímu přídavku šumu během procesu trénování. Proto bude výkon standardní neuronové sítě ekvivalentní CNN vždy nižší.

Rozpoznávací algoritmus pro datovou sadu GTSRB

Německý srovnávací test rozpoznávání dopravních značek (German Traffic Sign Recognition Benchmark, GTSRB) byl úkol pro klasifikaci více tříd a jednoho snímku, který se konal na mezinárodní konferenci International Joint Conference on Neural Networks (IJCNN) 2011 a měl následující požadavky:

• 51 840 obrázků německých dopravních značek ve 43 třídách (obrázky 14 a 15)
• Velikost obrázků se pohybuje od 15×15 do 222×193
• Obrázky jsou seskupeny podle tříd a stop s nejméně 30 obrázky na stopu
• Obrázky jsou k dispozici jako barevné obrázky (RGB), funkce HOG, funkce Haar a barevné histogramy
• Soutěží se pouze pro klasifikační algoritmus; algoritmus pro nalezení oblasti zájmu na snímku není vyžadován
• Časové informace testovacích sekvencí nejsou sdíleny, takže časovou dimenzi nelze v klasifikačním algoritmu použít

Obrázek 14: Ideální dopravní značky GTSRB

Obrázek 15: Dopravní značky GTSRB se znehodnocením

Algoritmus Kadence pro rozpoznávání dopravních značek v datové sadě GTSRB

Kadence vyvinul v prostředí MATLAB různé algoritmy pro rozpoznávání dopravních značek pomocí datové sady GTSRB, přičemž začal se základní konfigurací založenou na známé práci o rozpoznávání značek . Míra správné detekce 99,24 % a výpočetní náročnost téměř >50 milionů násobků na značku je na obrázku 16 znázorněna jako tlustý zelený bod. Společnost Cadence dosáhla významně lepších výsledků pomocí našeho nového vlastního přístupu Hierarchical CNN. V tomto algoritmu bylo 43 dopravních značek rozděleno do pěti rodin. Celkem jsme implementovali šest menších CNN. První CNN rozhoduje, do které rodiny přijatá dopravní značka patří. Jakmile je rodina značky známa, spustí se CNN (jedna ze zbývajících pěti) odpovídající zjištěné rodině, která rozhodne o dopravní značce v rámci této rodiny. Pomocí tohoto algoritmu dosáhla společnost Cadence správné míry detekce 99,58 %, což je dosud nejlepší dosažená míra CDR na GTSRB.

Algoritmus pro kompromis mezi výkonem a složitostí

Pro kontrolu složitosti CNN ve vestavěných aplikacích vyvinula společnost Cadence také vlastní algoritmus využívající rozklad vlastních čísel, který redukuje natrénovanou CNN na její kanonický rozměr. Pomocí tohoto algoritmu se nám podařilo drasticky snížit složitost CNN bez degradace výkonu nebo s malým řízeným snížením CDR. Obrázek 16 ukazuje dosažené výsledky:

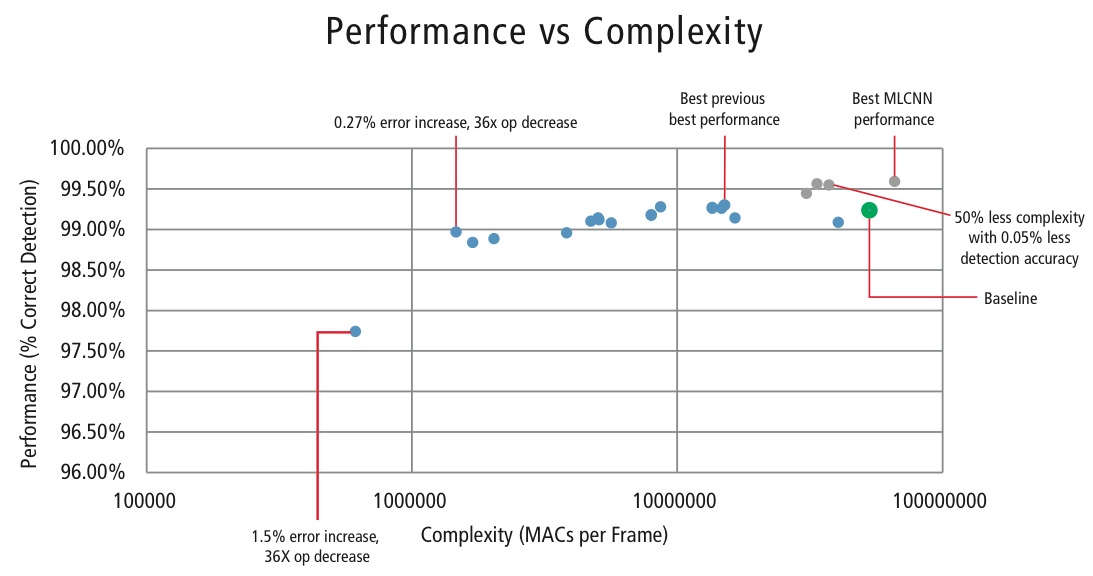
Obrázek 16: Graf závislosti výkonu na složitosti pro různé konfigurace CNN k detekci dopravních značek v datové sadě GTSRB

Zelený bod na obrázku 16 je základní konfigurace. Tato konfigurace je poměrně blízká konfiguraci navržené v Reference . Vyžaduje 53 MMAC na snímek pro chybovost 0,76 %.

• Druhý bod zleva vyžaduje 1,47 milionu MAC na snímek pro chybovost 1,03 %, tj, při zvýšení chybovosti o 0,27 % se požadavek na MAC snížil 36,14krát.
• Konec bodu zleva vyžaduje 0,61 MMAC na snímek pro dosažení chybovosti 2,26 %, tj. počet MAC se snížil 86,4krát.
• Body vyznačené modře jsou pro jednoúrovňovou CNN, zatímco body vyznačené červeně jsou pro hierarchickou CNN. Nejlepšího výkonu 99,58 % dosahuje hierarchická CNN.

CNN ve vestavných systémech

Jak je vidět na obrázku 5, subsystém vidění vyžaduje kromě CNN také velké množství zpracování obrazu. Aby bylo možné provozovat CNN na vestavném systému s omezeným příkonem, který podporuje zpracování obrazu, měl by splňovat následující požadavky:

• Dostupnost vysokého výpočetního výkonu:
• Větší šířka pásma pro načítání/ukládání: V případě plně propojené vrstvy používané pro účely klasifikace se každý koeficient použije při násobení pouze jednou. Požadavek na šířku pásma pro načítání a ukládání je tedy větší než počet MAC prováděných procesorem.
• Nízké požadavky na dynamický výkon: Systém by měl spotřebovávat méně energie. Pro řešení tohoto problému je nutná implementace s pevnou řádovou čárkou, která klade požadavek na splnění požadavků na výkon s použitím minimálního možného konečného počtu bitů.
• Pružnost:

Protože výpočetní zdroje jsou ve vestavných systémech vždy omezením, pokud případ použití umožňuje malé zhoršení výkonu, je užitečné mít algoritmus, který může dosáhnout obrovské úspory výpočetní složitosti za cenu řízeného malého zhoršení výkonu. Práce společnosti Cadence na algoritmu pro dosažení kompromisu mezi složitostí a výkonem, jak je vysvětleno v předchozí části, má tedy velký význam pro implementaci CNN ve vestavěných systémech.

CNN na procesorech Tensilica

Procesor Tensilica Vision P5 DSP je vysoce výkonný DSP s nízkou spotřebou speciálně navržený pro zpracování obrazu a počítačového vidění. DSP má architekturu VLIW s podporou SIMD. Má pět emisních slotů v instrukčním slově o délce až 96 bitů a každý cyklus může z paměti načíst až 1024bitová slova. Vnitřní registry a operační jednotky mají rozsah od 512 bitů do 1536 bitů, přičemž data jsou reprezentována jako 16, 32 nebo 64 řezů 8b, 16b, 24b, 32b nebo 48b pixelových dat.

DSP řeší všechny výzvy pro implementaci CNN ve vestavěných systémech, jak bylo uvedeno v předchozí části.

• Dostupnost vysokého výpočetního výkonu: Kromě pokročilé podpory pro implementaci zpracování obrazového signálu má DSP podporu instrukcí pro všechny fáze CNN. Pro operace konvoluce má velmi bohatou instrukční sadu podporující operace násobení/násobení-akumulace s podporou operací 8b x 8b, 8b x 16b a 16b x 16b pro data se znaménkem/bez znaménka. Dokáže provést až 64 operací násobení/násobení a akumulace 8b x 16b a 8b x 8b v jednom cyklu a 32 operací násobení/násobení a akumulace 16b x 16b v jednom cyklu. Pro funkce maximálního sdružování a ReLU má DSP instrukce pro provedení 64 8bitových porovnání v jednom cyklu. Pro implementaci nelineárních funkcí s konečným rozsahem, jako je tanh a signum, má instrukce pro implementaci vyhledávací tabulky pro 64 7bitových hodnot v jednom cyklu. Ve většině případů se instrukce pro porovnávání a vyhledávací tabulku plánují paralelně s instrukcemi násobení/násobení-akumulace a nezabírají žádné cykly navíc.
• Větší šířka pásma pro načítání/ukládání: DSP může provádět až dvě 512bitové operace načítání/ukládání za cyklus.
• Nízká potřeba dynamického výkonu: DSP je stroj s pevnou řádovou čárkou. Díky flexibilnímu zpracování různých typů dat lze dosáhnout plného výkonu a energetické výhody smíšených 16b a 8b výpočtů při minimální ztrátě přesnosti.
• Flexibilita: Vzhledem k tomu, že DSP je programovatelný procesor, lze systém upgradovat na novou verzi pouhým provedením upgradu firmwaru.
• Floating Point:

Procesor Vision P5 DSP se dodává s kompletní sadou softwarových nástrojů, která zahrnuje vysoce výkonný kompilátor jazyka C/C++ s automatickou vektorizací a plánováním pro podporu architektury SIMD a VLIW bez nutnosti psát jazyk assembleru. Tato komplexní sada nástrojů zahrnuje také linker, assembler, debugger, profiler a grafické vizualizační nástroje. Komplexní simulátor instrukční sady (ISS) umožňuje návrháři rychle simulovat a vyhodnocovat výkon. Při práci s rozsáhlými systémy nebo dlouhými testovacími vektory dosahuje volitelný rychlý funkční simulátor TurboXim rychlostí 40x až 80x vyšších než ISS pro efektivní vývoj softwaru a ověření funkčnosti.

Cadence implementoval na DSP jednovrstvou architekturu CNN pro rozpoznávání německých dopravních značek. Společnost Cadence dosáhla u této architektury CDR 99,403 % s 16bitovou kvantizací pro datové vzorky a 8bitovou kvantizací pro koeficienty ve všech vrstvách. Má dvě konvoluční vrstvy, tři plně propojené vrstvy, čtyři vrstvy ReLU, tři vrstvy max pooling a jednu nelineární vrstvu tanh. Společnost Cadence dosáhla průměrného výkonu 38,58 MACs/cyklus pro celou síť včetně cyklů pro všechny vrstvy max pooling, tanh a ReLU. Společnost Cadence dosáhla nejlepšího výkonu 58,43 MACs/cyklus pro třetí vrstvu včetně cyklů pro funkce tanh a ReLU. Tento DSP běžící na 600 MHz dokáže zpracovat více než 850 dopravních značek za jednu sekundu.

Budoucnost CNN

Mezi slibné oblasti výzkumu neuronových sítí patří rekurentní neuronové sítě (RNN) využívající dlouhou krátkodobou paměť (LSTM). Tyto oblasti přinášejí současný stav techniky v úlohách rozpoznávání časových řad, jako je rozpoznávání řeči a rozpoznávání rukopisu. RNN/autoenkodéry jsou také schopny generovat rukopis/řeč/obrázky s určitým známým rozložením ,,,,.

Hluboké sítě víry, další slibný typ sítě využívající omezené Boltzmanovy stroje (RMB)/autokodéry, je možné trénovat chamtivě, po jedné vrstvě, a proto jsou snadněji trénovatelné pro velmi hluboké sítě ,.

Závěr

CNN podávají nejlepší výkon v problémech rozpoznávání vzorů/obrazů a v některých případech dokonce předčí člověka. Společnost Cadence dosáhla pomocí vlastních algoritmů a architektur s CNN nejlepších výsledků v oboru. Vyvinuli jsme hierarchické CNN pro rozpoznávání dopravních značek v GTSRB a dosáhli jsme nejlepšího výkonu, jaký kdy byl na této datové sadě dosažen. Vyvinuli jsme další algoritmus pro kompromis mezi výkonem a složitostí a podařilo se nám dosáhnout 86násobného snížení složitosti při zhoršení CDR o méně než 2 %. DSP Tensilica Vision P5 pro zobrazování a počítačové vidění od společnosti Cadence má kromě funkcí potřebných pro zpracování obrazového signálu také všechny funkce potřebné k implementaci CNN. Při běhu DSP na frekvenci 600 MHz lze provést více než 850 rozpoznávání dopravních značek. DSP Tensilica Vision P5 od společnosti Cadence má téměř ideální sadu funkcí pro provoz CNN.

„Umělá neuronová síť“. Wikipedie. https://en.wikipedia.org/wiki/Artificial_neural_network

Karpathy, Andrej. 2015. „Neuronové sítě, část 1: Nastavení architektury“. Poznámky pro CS231n Convolutional Neural Networks for Visual Recognition, Stanford University. http://cs231n.github.io/neural-networks-1/

„Konvoluční neuronová síť“. Wikipedia. https://en.wikipedia.org/wiki/Convolutional_neural_network

Sermanet, Pierre a Yann LeCun. 2011. „Rozpoznávání dopravních značek pomocí sítí s více měřítky“. Courant Institute of Mathematical Sciences, New York University. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6033589

Ciresan, Dan, Ueli Meier a Jürgen Schmidhuber. 2012. „Vícesloupcové hluboké neuronové sítě pro klasifikaci obrazu“. 2012 IEEE Conference on Computer Vision and Pattern Recognition (New York, NY: Institute of Electrical and Electronics Engineers (IEEE)). http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6248110

Ciresan, Dan, Ueli Meier, Jonathan Masci, Luca M. Gambardella a Jurgen Schmidhuber. 2011. „Flexibilní, vysoce výkonné konvoluční neuronové sítě pro klasifikaci obrazu“. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence-Volume Two: 1237-1242. Získáno 17. listopadu 2013. http://people.idsia.ch/~juergen/ijcai2011.pdf

Lawrence, Steve, C. Lee Giles, Ah Chung Tsoi a Andrew D. Back. 1997. „Rozpoznávání tváří: A Convolutional Neural Network Approach“. IEEE Transactions on Neural Networks, svazek 8; vydání 1. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=554195

Russakovsky, O. et al. 2014. „ImageNet Large Scale Visual Recognition Challenge“. International Journal of Computer Vision. http://link.springer.com/article/10.1007/s11263-015-0816-y#

Ovtcharov, Kalin, Olatunji Ruwarse, Joo-Young Kim et al. 22. února 2015. „Akcelerace hlubokých konvolučních sítí pomocí specializovaného hardwaru“. Microsoft Research. http://research-srv.microsoft.com/pubs/240715/CNN%20Whitepaper.pdf

Stallkamp, J., M. Schlipsing, J. Salmen a C. Igel. „Člověk versus počítač: Benchmarking Machine Learning Algorithms For Traffic Sign Application“. IJCNN 2011. http://www.sciencedirect.com/science/article/pii/S0893608012000457

Hochreiter, Sepp a Jürgen Schmidhuber. 1997. „Dlouhodobá krátkodobá paměť.“ Neural Computation, 9(8):1735-1780. ftp://ftp.idsia.ch/pub/juergen/lstm.pdf

Graves, Alex. 2014. „Generování sekvencí pomocí rekurentních neuronových sítí“. http://arxiv.org/abs/1308.0850

Schmidhuber, Jurgen. 2015. „Rekurentní neuronové sítě.“ http://people.idsia.ch/~juergen/rnn.html

Olshausen, Bruno A. a David J. Field. 1996. „Vznik vlastností receptivního pole jednoduchých buněk učením řídkého kódu pro přirozené obrazy“. Nature 381.6583: 607-609. http://www.nature.com/nature/journal/v381/n6583/abs/381607a0.html

Hinton, G. E. a Salakhutdinov, R. R. 2006. „Snižování dimenzionality dat pomocí neuronových sítí“. Science vol. 313 no. 5786 pp. 504-507. http://www.sciencemag.org/content/suppl/2006/08/04/313.5786.504.DC1.

Hinton, Geoffrey E. 2009. „Deep belief networks“ (Hluboké sítě víry). Scholarpedia, 4(5):5947.
http://www.scholarpedia.org/article/Deep_belief_networks