Klouzavé průměry v programu pandas

Úvod
Klouzavý průměr, nazývaný také klouzavý nebo průběžný průměr, se používá k analýze dat časových řad pomocí výpočtu průměrů různých podmnožin kompletního souboru dat. Protože jde o výpočet průměru souboru dat v čase, nazývá se také klouzavý průměr (MM) nebo klouzavý průměr.
Klouzavý průměr lze vypočítat různými způsoby, ale jedním z těchto způsobů je vzít pevnou podmnožinu z úplné řady čísel. První klouzavý průměr se vypočítá zprůměrováním první pevné podmnožiny čísel a poté se tato podmnožina změní posunem vpřed k další pevné podmnožině (zahrnutím budoucí hodnoty do podskupiny a zároveň vyloučením předchozího čísla z řady).
Klouzavý průměr se většinou používá u dat časových řad, aby zachytil krátkodobé výkyvy a zároveň se zaměřil na dlouhodobější trendy.
Několika příklady dat časových řad mohou být ceny akcií, zprávy o počasí, kvalita ovzduší, hrubý domácí produkt, zaměstnanost atd.
Obecně klouzavý průměr vyhlazuje data.
Klouzavý průměr je základem mnoha algoritmů a jedním z takových algoritmů je model ARIMA (Autoregressive Integrated Moving Average Model), který využívá klouzavé průměry k předpovědím dat časových řad.
Existují různé typy klouzavých průměrů:
-
Jednoduchý klouzavý průměr (SMA): Jednoduchý klouzavý průměr (SMA) používá klouzavé okno pro průměr za stanovený počet časových období. Jedná se o rovnoměrně vážený průměr z předchozích n údajů.
Pro bližší pochopení SMA si uveďme příklad, posloupnost n hodnot:

tedy rovnoměrně vážený klouzavý průměr pro n datových bodů bude v podstatě průměrem předchozích M datových bodů, kde M je velikost klouzavého okna:

Podobně pro výpočet následujících hodnot klouzavého průměru bude do součtu přidána nová hodnota a hodnota předchozího časového období bude vypuštěna, protože máte průměr předchozích časových období, takže není nutné pokaždé provádět úplný součet:

- Kumulativní klouzavý průměr (CMA): Na rozdíl od jednoduchého klouzavého průměru, který při přidání nového pozorování vyřadí nejstarší pozorování, kumulativní klouzavý průměr bere v úvahu všechna předchozí pozorování. CMA není příliš dobrou technikou pro analýzu trendů a vyhlazování dat. Důvodem je, že průměruje všechna předchozí data až do aktuálního datového bodu, tedy rovnoměrně vážený průměr posloupnosti n hodnot:



- Exponenciální klouzavý průměr (EMA): Na rozdíl od SMA a CMA dává exponenciální klouzavý průměr větší váhu nedávným cenám, v důsledku čehož může být lepším modelem nebo lépe a rychleji zachycovat pohyb trendu. Reakce EMA je přímo úměrná struktuře dat.
Protože EMA dává větší váhu nedávným datům než starším, reaguje na nejnovější změny cen ve srovnání s SMA, díky čemuž jsou výsledky z EMA aktuálnější, a proto je EMA upřednostňován před ostatními technikami.
Dost teorie, že? Přejděme k praktické implementaci klouzavého průměru.
Implementace klouzavého průměru na datech časové řady
Jednoduchý klouzavý průměr (SMA)
Nejprve vytvoříme fiktivní data časové řady a zkusíme implementovat SMA pouze pomocí Pythonu.
Předpokládejme, že existuje poptávka po produktu a je sledována po dobu 12 měsíců (1 rok) a je třeba najít klouzavé průměry pro 3 a 4 měsíční okenní období.
Import modulu
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| měsíc | poptávka | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Vypočítáme SMA pro velikost okna 3, což znamená, že při výpočtu klouzavého průměru budete pokaždé uvažovat tři hodnoty a pro každou novou hodnotu bude nejstarší hodnota ignorována.
Pro realizaci použijete funkci pandas iloc, protože potřebujete sloupec demand, zafixujete jeho pozici ve funkci iloc, zatímco řádek bude proměnná i, kterou budete iterovat, dokud nedosáhnete konce datového rámce.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| měsíc | poptávka | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Pro kontrolu příčetnosti použijeme také pandas vestavěnou funkci rolling a zjistíme, zda se shoduje s naším vlastním jednoduchým klouzavým průměrem založeným na pythonu.
df = df.iloc.rolling(window=3).mean()df.head()| měsíc | poptávka | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, takže jak vidíte, vlastní a pandí klouzavé průměry se přesně shodují, což znamená, že vaše implementace SMA byla správná.
Nechte si také rychle vypočítat jednoduchý klouzavý průměr pro window_size4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| měsíc | poptávka | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| měs. | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN | |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN | |
| 3 | 4 | 300 | 282,7 | 282.666667 | 284.5 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299,333333 | 289,5 | 289,5 |
Nyní vykreslíte data klouzavých průměrů, která jste vypočítali.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>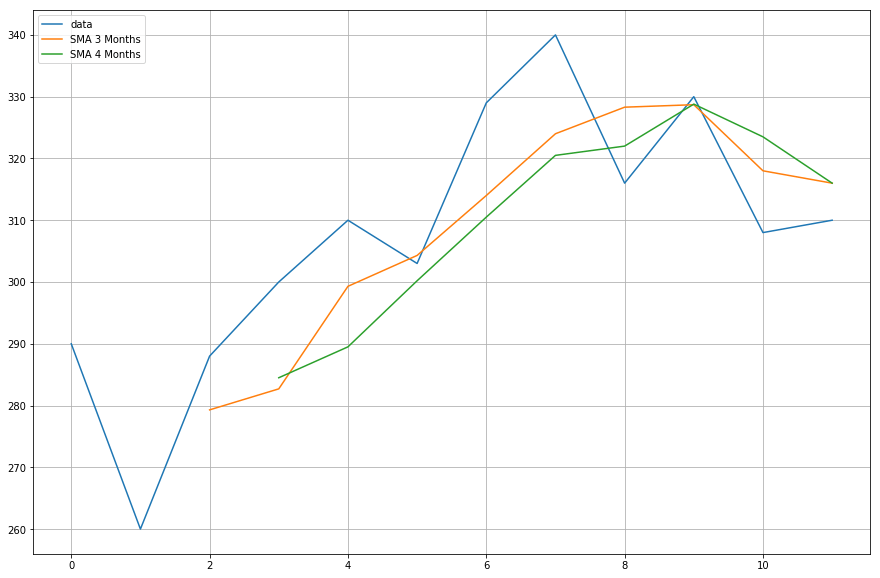
Kumulativní klouzavý průměr
Myslím, že nyní jsme připraveni přejít k reálné sadě dat.
Pro kumulativní klouzavý průměr použijeme air quality dataset, který si můžete stáhnout z tohoto odkazu.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Předběžné zpracování je nezbytným krokem vždy, když pracujete s daty. U číselných dat je jedním z nejběžnějších kroků předzpracování kontrola hodnot NaN (Null). Pokud existují nějaké hodnoty NaN, můžete je nahradit buď 0, nebo průměrem, nebo předchozími či následujícími hodnotami, nebo je dokonce vypustit. Ačkoli nahrazení je obvykle lepší volbou než jejich vypuštění, vzhledem k tomu, že tato datová sada má málo NULL hodnot, jejich vypuštění nebude mít vliv na kontinuitu řady.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Z výše uvedeného výstupu můžete pozorovat, že ve všech sloupcích je asi 114 hodnot NaN, nicméně zjistíte, že všechny jsou na konci časové řady, takže je rychle vypustíme.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Na Temperature column (T) budete aplikovat kumulativní klouzavý průměr, proto tento sloupec rychle oddělme od kompletních dat.
df_T = pd.DataFrame(df.iloc)df_T.head()
Nyní, použijete metodu pandas expanding pro zjištění kumulativního průměru výše uvedených dat. Pokud si vzpomínáte z úvodu, na rozdíl od prostého klouzavého průměru bere kumulativní klouzavý průměr při výpočtu průměru v úvahu všechny předcházející hodnoty.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13. Pokud si vzpomínáte z úvodu, kumulativní klouzavý průměr bere v úvahu všechny předcházející hodnoty.6 | NaN |
| 1 | 13,3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11,0 | 12,450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Časové řady dat se vykreslují s ohledem na čas, proto sloupec data a času spojíme a převedeme na objekt datetime. K tomu použijeme modul datetime z Pythonu (Zdroj: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Změníme index datového rámce temperature s datetime.
df_T.index = df.DateTimeVyneseme nyní do grafu aktuální teplotu a kumulativní klouzavý průměr wrt. čas.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponenciální klouzavý průměr
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DateTime | |||
| 2004-.03-10 18:00:00 | 13.6 | NaN | 13.600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>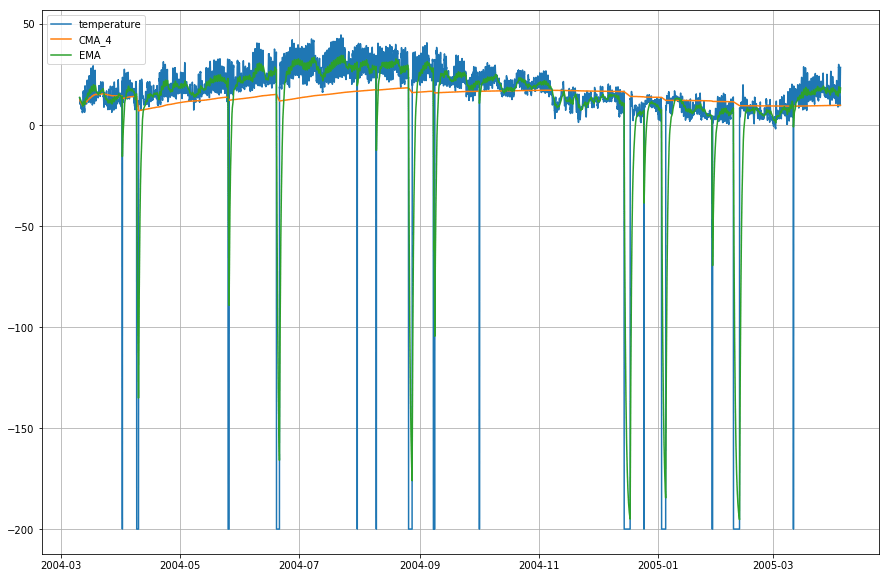
Wow! Jak tedy můžete z výše uvedeného grafu vypozorovat, Exponential Moving Average (EMA) odvádí vynikající práci při zachycení vzoru dat, zatímco Cumulative Moving Average (CMA) chybí značná rezerva.
Jděte dál!
Gratuluji k dokončení výuky.
Tento tutoriál byl dobrým výchozím bodem, jak můžete vypočítat klouzavé průměry z dat a dát jim smysl.
Zkuste napsat kód kumulativního a exponenciálního klouzavého průměru v Pythonu bez použití knihovny pandas. Získáte tak mnohem hlubší znalosti o tom, jak se počítají a v čem se od sebe liší.
Stále je s čím experimentovat. Zkuste spočítat částečnou autokorelaci mezi vstupními daty a klouzavým průměrem a pokuste se mezi nimi najít nějaký vztah.
Pokud se chcete o DataFrame v knihovně pandas dozvědět více, zúčastněte se interaktivního kurzu DataCamp pandas Foundations.
.