Dieser Artikel wurde ursprünglich auf der Website von Cadence veröffentlicht. Er wird hier mit der Erlaubnis von Cadence nachgedruckt.

Convolutional Neural Networks (CNNs) werden häufig bei Problemen der Muster- und Bilderkennung eingesetzt, da sie im Vergleich zu anderen Techniken eine Reihe von Vorteilen haben. In diesem Whitepaper werden die Grundlagen von CNNs behandelt, einschließlich einer Beschreibung der verschiedenen verwendeten Schichten. Am Beispiel der Erkennung von Verkehrsschildern werden die Herausforderungen des allgemeinen Problems erörtert und von Cadence entwickelte Algorithmen und Implementierungssoftware vorgestellt, die einen Kompromiss zwischen Rechenaufwand und Energiebedarf und einer geringfügigen Verschlechterung der Erkennungsraten für Verkehrsschilder ermöglichen. Wir skizzieren die Herausforderungen beim Einsatz von CNNs in eingebetteten Systemen und stellen die Schlüsseleigenschaften des Cadence® Tensilica® Vision P5 Digitalen Signalprozessors (DSP) für Imaging und Computer Vision und die Software vor, die ihn für CNN-Anwendungen in vielen Bereichen der Bildgebung und verwandten Erkennungsaufgaben so geeignet machen.

Was ist ein CNN?

Ein neuronales Netzwerk ist ein System von miteinander verbundenen künstlichen „Neuronen“, die untereinander Nachrichten austauschen. Die Verbindungen haben numerische Gewichte, die während des Trainingsprozesses eingestellt werden, so dass ein richtig trainiertes Netzwerk korrekt reagiert, wenn es ein Bild oder Muster erkennt. Das Netzwerk besteht aus mehreren Schichten von merkmalserkennenden „Neuronen“. Jede Schicht hat viele Neuronen, die auf verschiedene Kombinationen von Eingaben aus den vorherigen Schichten reagieren. Wie in Abbildung 1 dargestellt, sind die Schichten so aufgebaut, dass die erste Schicht eine Reihe von primitiven Mustern in der Eingabe erkennt, die zweite Schicht Muster von Mustern, die dritte Schicht Muster dieser Muster und so weiter. Typische CNNs verwenden 5 bis 25 verschiedene Schichten zur Mustererkennung.

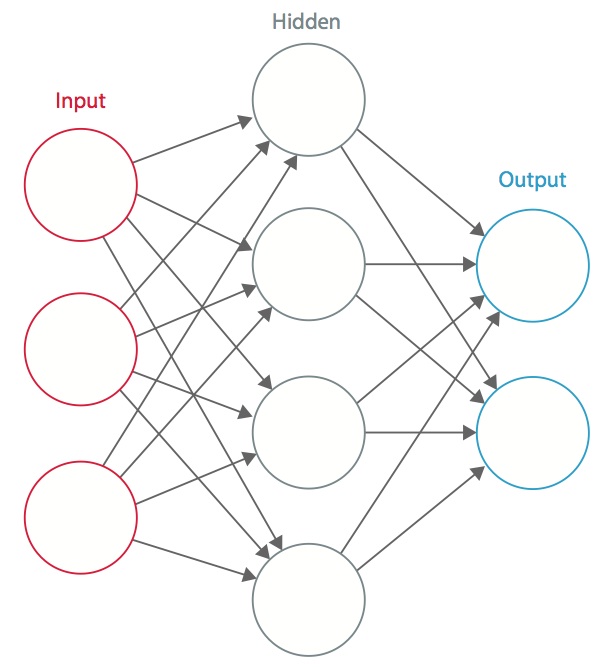
Abbildung 1: Ein künstliches neuronales Netz

Das Training erfolgt anhand eines „markierten“ Datensatzes von Eingaben in einem breiten Sortiment von repräsentativen Eingabemustern, die mit ihrer beabsichtigten Ausgabereaktion gekennzeichnet sind. Beim Training werden allgemeine Methoden verwendet, um iterativ die Gewichte für Zwischen- und Endneuronen zu bestimmen. Abbildung 2 zeigt den Trainingsprozess auf Blockebene.

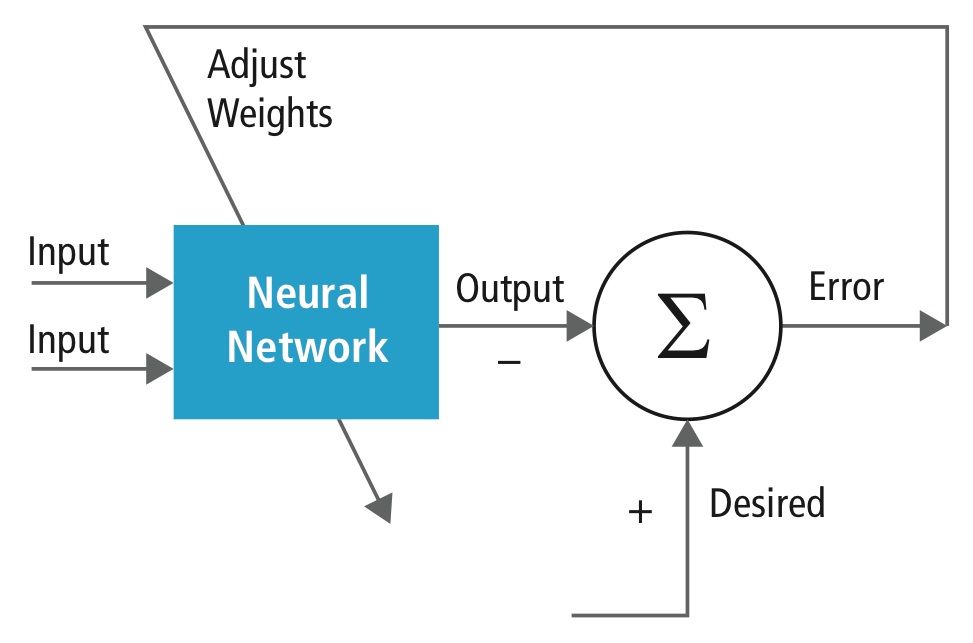
Abbildung 2: Training von neuronalen Netzen

Neuronale Netze sind von biologischen neuronalen Systemen inspiriert. Die grundlegende Recheneinheit des Gehirns ist ein Neuron, und sie sind mit Synapsen verbunden. Abbildung 3 vergleicht ein biologisches Neuron mit einem grundlegenden mathematischen Modell.

Abbildung 3: Darstellung eines biologischen Neurons (oben) und seines mathematischen Modells (unten)

In einem realen tierischen neuronalen System empfängt ein Neuron Eingangssignale von seinen Dendriten und produziert Ausgangssignale entlang seines Axons. Das Axon verzweigt sich und verbindet sich über Synapsen mit Dendriten anderer Neuronen. Wenn die Kombination von Eingangssignalen eine bestimmte Schwellenbedingung unter seinen Eingangsdendriten erreicht, wird das Neuron ausgelöst und seine Aktivierung wird an die Nachfolge-Neuronen weitergegeben.

Im Rechenmodell des neuronalen Netzes interagieren die Signale, die entlang der Axone wandern (z.B. x0), multiplikativ (z.B. w0x0) mit den Dendriten des anderen Neurons auf der Grundlage der synaptischen Stärke an dieser Synapse (z.B. w0). Die synaptischen Gewichte sind lernbar und steuern den Einfluss des einen oder anderen Neurons. Die Dendriten leiten das Signal an den Zellkörper weiter, wo sie alle summiert werden. Wenn die Endsumme über einem bestimmten Schwellenwert liegt, feuert das Neuron und sendet einen Spike entlang seines Axons. In dem Rechenmodell wird davon ausgegangen, dass der genaue Zeitpunkt des Feuerns keine Rolle spielt und nur die Frequenz des Feuerns Informationen übermittelt. Auf der Grundlage der Interpretation des Ratencodes wird die Feuerungsrate des Neurons mit einer Aktivierungsfunktion ƒ modelliert, die die Frequenz der Spikes entlang des Axons darstellt. Eine übliche Wahl der Aktivierungsfunktion ist sigmoidal. Zusammenfassend lässt sich sagen, dass jedes Neuron das Punktprodukt von Eingaben und Gewichten berechnet, die Vorspannung addiert und Nichtlinearität als Auslösefunktion anwendet (z. B. nach einer sigmoiden Antwortfunktion).

Ein CNN ist ein Spezialfall des oben beschriebenen neuronalen Netzes. Ein CNN besteht aus einer oder mehreren Faltungsschichten, oft mit einer Unterabtastungsschicht, auf die eine oder mehrere vollständig verbundene Schichten wie in einem normalen neuronalen Netz folgen.

Der Entwurf eines CNN ist durch die Entdeckung eines visuellen Mechanismus, des visuellen Cortex, im Gehirn motiviert. Der visuelle Kortex enthält viele Zellen, die für die Erkennung von Licht in kleinen, sich überlappenden Teilbereichen des Gesichtsfeldes, den so genannten rezeptiven Feldern, verantwortlich sind. Diese Zellen fungieren als lokale Filter für den Eingaberaum, und die komplexeren Zellen haben größere rezeptive Felder. Die Faltungsschicht in einem CNN führt die Funktion aus, die von den Zellen im visuellen Kortex ausgeführt wird.

Ein typisches CNN zur Erkennung von Verkehrszeichen ist in Abbildung 4 dargestellt. Jedes Merkmal einer Schicht erhält Eingaben von einer Reihe von Merkmalen, die sich in einer kleinen Nachbarschaft in der vorherigen Schicht befinden, die als lokales rezeptives Feld bezeichnet wird. Mit lokalen rezeptiven Feldern können Merkmale elementare visuelle Merkmale extrahieren, wie z. B. orientierte Kanten, Endpunkte, Ecken usw., die dann von den höheren Schichten kombiniert werden.

Im traditionellen Modell der Muster-/Bilderkennung sammelt ein von Hand entworfener Merkmalsextraktor relevante Informationen aus der Eingabe und eliminiert irrelevante Variabilitäten. Auf den Extraktor folgt ein trainierbarer Klassifikator, ein neuronales Standardnetzwerk, das die Merkmalsvektoren in Klassen einteilt.

In einem CNN spielen Faltungsschichten die Rolle des Merkmalsextraktors. Sie werden jedoch nicht von Hand entworfen. Die Gewichte des Faltungsfilterkerns werden im Rahmen des Trainingsprozesses festgelegt. Faltungsschichten sind in der Lage, lokale Merkmale zu extrahieren, weil sie die rezeptiven Felder der verborgenen Schichten auf lokale Merkmale beschränken.

Abbildung 4: Typisches Blockdiagramm eines CNN

CNNs werden in einer Vielzahl von Bereichen eingesetzt, darunter Bild- und Mustererkennung, Spracherkennung, Verarbeitung natürlicher Sprache und Videoanalyse. Es gibt eine Reihe von Gründen, warum Faltungsneuronale Netze immer wichtiger werden. Bei herkömmlichen Modellen zur Mustererkennung werden die Merkmalsextraktoren von Hand entworfen. Bei CNNs werden die Gewichte der Faltungsschicht, die für die Merkmalsextraktion verwendet wird, sowie der vollständig verbundenen Schicht, die für die Klassifizierung verwendet wird, während des Trainingsprozesses bestimmt. Die verbesserten Netzwerkstrukturen von CNNs führen zu Einsparungen beim Speicherbedarf und bei den Anforderungen an die Rechenkomplexität und bieten gleichzeitig eine bessere Leistung für Anwendungen, bei denen die Eingabe eine lokale Korrelation aufweist (z. B. Bild und Sprache).

Der hohe Bedarf an Rechenressourcen für das Training und die Auswertung von CNNs wird manchmal durch Grafikprozessoren (GPUs), DSPs oder andere Siliziumarchitekturen gedeckt, die für einen hohen Durchsatz und einen geringen Energieverbrauch bei der Ausführung der idiosynkratischen Muster der CNN-Berechnungen optimiert sind. Moderne Prozessoren wie der Tensilica Vision P5 DSP for Imaging and Computer Vision von Cadence verfügen über eine nahezu ideale Kombination von Rechen- und Speicherressourcen, die für die Ausführung von CNNs mit hoher Effizienz erforderlich sind.

In Anwendungen der Muster- und Bilderkennung wurden mit CNNs die bestmöglichen Erkennungsraten (CDRs) erzielt. So haben CNNs beispielsweise eine Erkennungsrate von 99,77 % mit der MNIST-Datenbank für handgeschriebene Ziffern, eine Erkennungsrate von 97,47 % mit dem NORB-Datensatz für 3D-Objekte und eine Erkennungsrate von 97,6 % bei ~5600 Bildern mit mehr als 10 Objekten erzielt. CNNs erbringen nicht nur die beste Leistung im Vergleich zu anderen Erkennungsalgorithmen, sondern übertreffen den Menschen sogar in Fällen wie der Klassifizierung von Objekten in feinkörnige Kategorien wie eine bestimmte Hunderasse oder Vogelart.

Abbildung 5 zeigt eine typische Bildverarbeitungsalgorithmus-Pipeline, die aus vier Stufen besteht: Vorverarbeitung des Bildes, Erkennung von Regionen von Interesse (ROI), die wahrscheinliche Objekte enthalten, Objekterkennung und Bildverarbeitungsentscheidung. Der Vorverarbeitungsschritt hängt in der Regel von den Details der Eingabe ab, insbesondere vom Kamerasystem, und wird oft in einer fest verdrahteten Einheit außerhalb des Bildverarbeitungssubsystems implementiert. Die Entscheidungsfindung am Ende der Pipeline bezieht sich in der Regel auf erkannte Objekte. Sie kann zwar komplexe Entscheidungen treffen, doch werden dabei viel weniger Daten verarbeitet, so dass diese Entscheidungen in der Regel keine rechenintensiven oder speicherintensiven Probleme darstellen. Die große Herausforderung liegt in den Stadien der Objekterkennung und -erkennung, wo CNNs jetzt einen großen Einfluss haben.

Abbildung 5: Bildverarbeitungsalgorithmus-Pipeline

Schichten von CNNs

Durch das Stapeln mehrerer und unterschiedlicher Schichten in einem CNN werden komplexe Architekturen für Klassifizierungsprobleme aufgebaut. Vier Arten von Schichten sind am gebräuchlichsten: Faltungsschichten, Pooling/Subsampling-Schichten, nicht-lineare Schichten und vollständig verbundene Schichten.

Faltungsschichten

Die Faltungsoperation extrahiert verschiedene Merkmale der Eingabe. Die erste Faltungsschicht extrahiert Low-Level-Merkmale wie Kanten, Linien und Ecken. Höhere Schichten extrahieren Merkmale auf höherer Ebene. Abbildung 6 veranschaulicht den Prozess der 3D-Faltung, der in CNNs verwendet wird. Die Eingabe hat die Größe N x N x D und wird mit H Kerneln gefaltet, die jeweils eine Größe von k x k x D haben. Die Faltung einer Eingabe mit einem Kernel ergibt ein Ausgangsmerkmal, und mit H Kerneln werden unabhängig voneinander H Merkmale erzeugt. Ausgehend von der linken oberen Ecke der Eingabe, wird jeder Kernel von links nach rechts, ein Element nach dem anderen, verschoben. Sobald die obere rechte Ecke erreicht ist, wird der Kernel um ein Element nach unten verschoben, und wieder wird der Kernel von links nach rechts verschoben, jeweils um ein Element. Dieser Vorgang wird so lange wiederholt, bis der Kernel die rechte untere Ecke erreicht hat. Für den Fall, dass N = 32 und k = 5 ist, gibt es 28 einzigartige Positionen von links nach rechts und 28 einzigartige Positionen von oben nach unten, die der Kernel einnehmen kann. Entsprechend diesen Positionen enthält jedes Merkmal in der Ausgabe 28×28 (d. h. (N-k+1) x (N-k+1)) Elemente. Für jede Position des Kernels in einem Gleitfensterprozess werden k x k x D Elemente der Eingabe und k x k x D Elemente des Kernels Element für Element multipliziert und akkumuliert. Um ein Element eines Ausgangsmerkmals zu erzeugen, sind also k x k x D Multiplikations-Akkumulations-Operationen erforderlich.

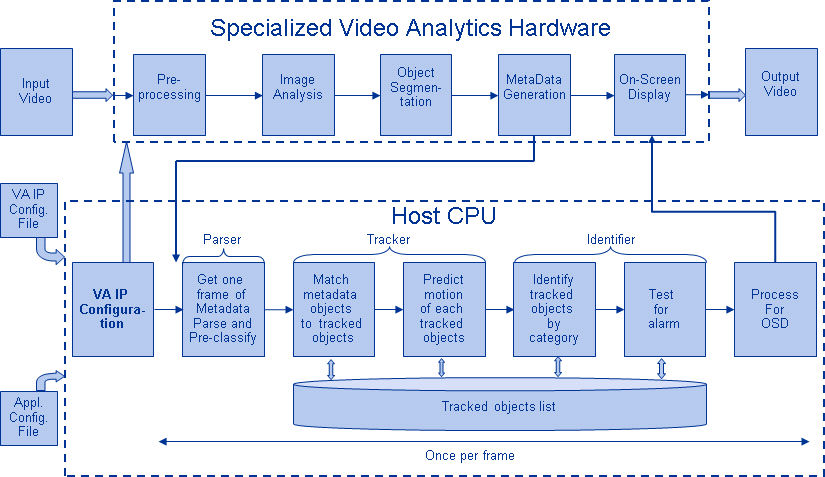
Abbildung 6: Bildliche Darstellung des Faltungsprozesses

Pooling/Subsampling-Schichten

Die Pooling/Subsampling-Schicht reduziert die Auflösung der Merkmale. Sie macht die Merkmale robust gegen Rauschen und Verzerrungen. Es gibt zwei Möglichkeiten des Pooling: Max-Pooling und Average-Pooling. In beiden Fällen wird die Eingabe in nicht überlappende zweidimensionale Räume unterteilt. In Abbildung 4 zum Beispiel ist Schicht 2 die Pooling-Schicht. Jedes Eingangsmerkmal ist 28×28 groß und wird in 14×14 Regionen der Größe 2×2 unterteilt. Beim Average-Pooling wird der Durchschnitt der vier Werte in der Region berechnet. Für das Max-Pooling wird der Maximalwert der vier Werte ausgewählt.

Abbildung 7 erläutert den Pooling-Prozess näher. Die Eingabe hat die Größe 4×4. Beim 2×2 Subsampling wird ein 4×4-Bild in vier nicht überlappende Matrizen der Größe 2×2 unterteilt. Beim Max-Pooling ist der Maximalwert der vier Werte in der 2×2-Matrix die Ausgabe. Beim Average-Pooling wird der Durchschnitt der vier Werte ausgegeben. Bitte beachten Sie, dass bei der Ausgabe mit dem Index (2,2) das Ergebnis der Mittelwertbildung ein Bruch ist, der auf die nächste ganze Zahl gerundet wurde.

Abbildung 7: Bildliche Darstellung von Max-Pooling und Average-Pooling

Nichtlineare Schichten

Neuronale Netze im Allgemeinen und CNNs im Besonderen stützen sich auf eine nichtlineare „Trigger“-Funktion, um die eindeutige Identifizierung wahrscheinlicher Merkmale auf jeder versteckten Schicht zu signalisieren. CNNs können eine Vielzahl spezifischer Funktionen verwenden – wie gleichgerichtete lineare Einheiten (ReLUs) und kontinuierliche (nichtlineare) Triggerfunktionen – um diese nichtlineare Triggerung effizient zu implementieren.

ReLU

Eine ReLU implementiert die Funktion y = max(x,0), so dass die Eingangs- und Ausgangsgrößen dieser Schicht gleich sind. Sie erhöht die nichtlinearen Eigenschaften der Entscheidungsfunktion und des gesamten Netzes, ohne die rezeptiven Felder der Faltungsschicht zu beeinträchtigen. Im Vergleich zu den anderen nichtlinearen Funktionen, die in CNNs verwendet werden (z. B. hyperbolischer Tangens, Absolutwert des hyperbolischen Tangens und Sigmoid), besteht der Vorteil einer ReLU darin, dass das Netz um ein Vielfaches schneller trainiert. Die ReLU-Funktionalität ist in Abbildung 8 dargestellt, wobei die Übertragungsfunktion oberhalb des Pfeils eingezeichnet ist.

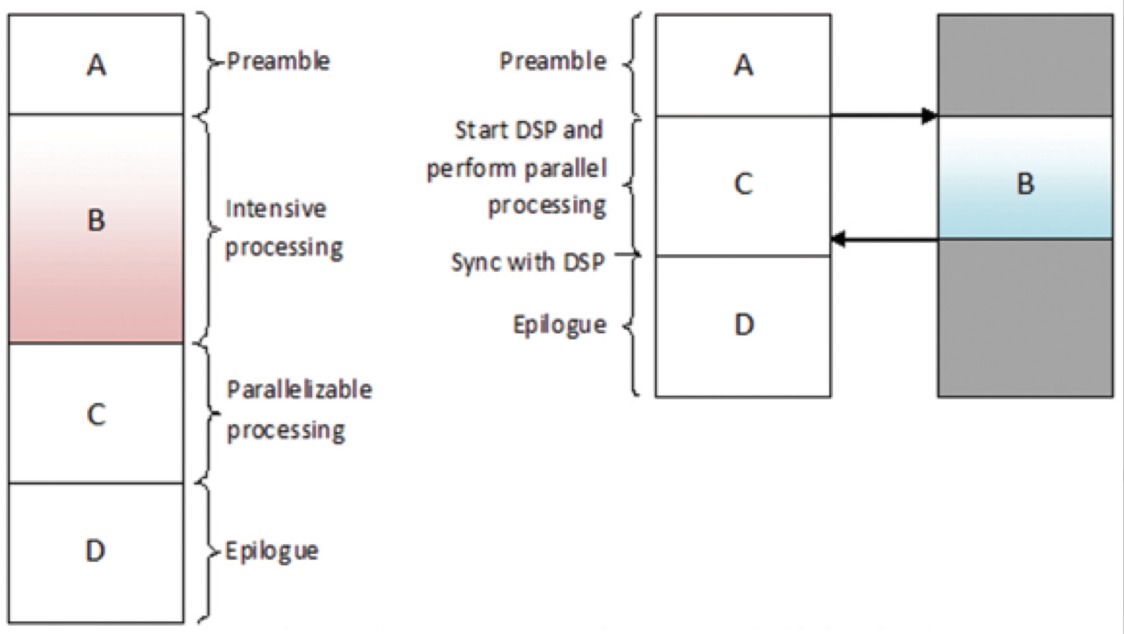
Abbildung 8: Bildliche Darstellung der ReLU-Funktionalität

Kontinuierliche (nichtlineare) Triggerfunktion

Die nichtlineare Schicht arbeitet Element für Element in jedem Merkmal. Eine kontinuierliche Triggerfunktion kann ein hyperbolischer Tangens (Abbildung 9), ein Absolutwert des hyperbolischen Tangens (Abbildung 10) oder ein Sigmoid (Abbildung 11) sein. Abbildung 12 zeigt, wie die Nichtlinearität Element für Element angewendet wird.

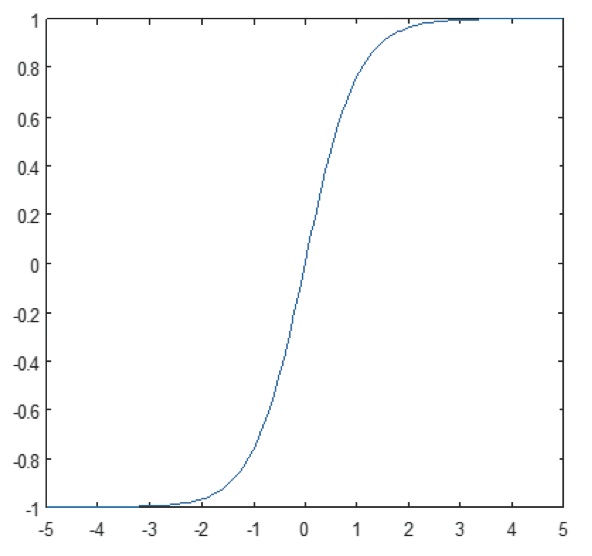
Abbildung 9: Plot der hyperbolischen Tangensfunktion

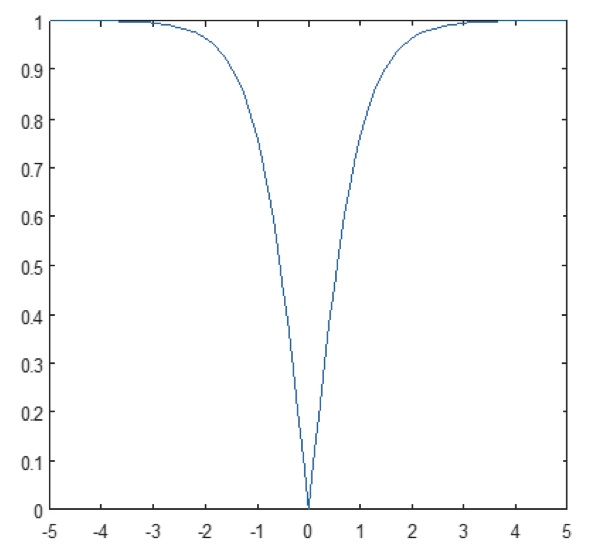
Abbildung 10: Plot der absoluten hyperbolischen Tangensfunktion

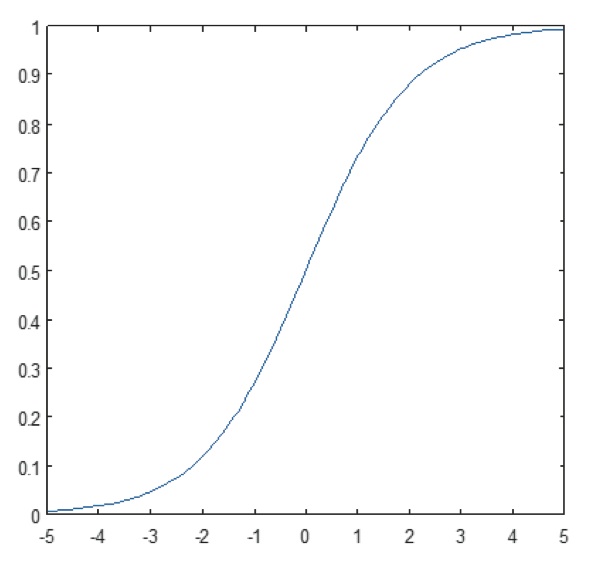
Abbildung 11: Plot der Sigmoidfunktion

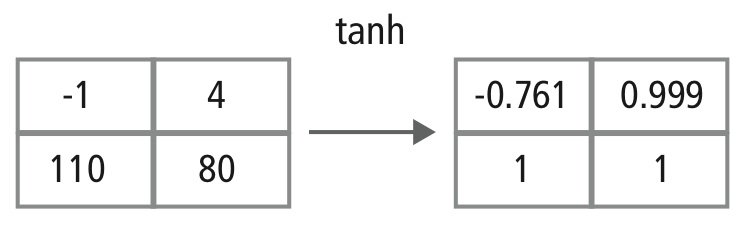
Abbildung 12: Bildliche Darstellung der tanh-Verarbeitung

Vollständig verbundene Schichten

Vollständig verbundene Schichten werden oft als letzte Schichten eines CNN verwendet. Diese Schichten addieren mathematisch eine Gewichtung der vorherigen Schicht von Merkmalen und geben die genaue Mischung der „Zutaten“ an, um ein bestimmtes Zielergebnis zu bestimmen. Im Falle einer vollständig verknüpften Schicht werden alle Elemente aller Merkmale der vorhergehenden Schicht bei der Berechnung jedes Elements jedes Ausgangsmerkmals verwendet.

Abbildung 13 erklärt die vollständig verknüpfte Schicht L. Schicht L-1 hat zwei Merkmale, von denen jedes 2×2 ist, d. h. vier Elemente hat. Schicht L hat zwei Merkmale mit jeweils einem Element.

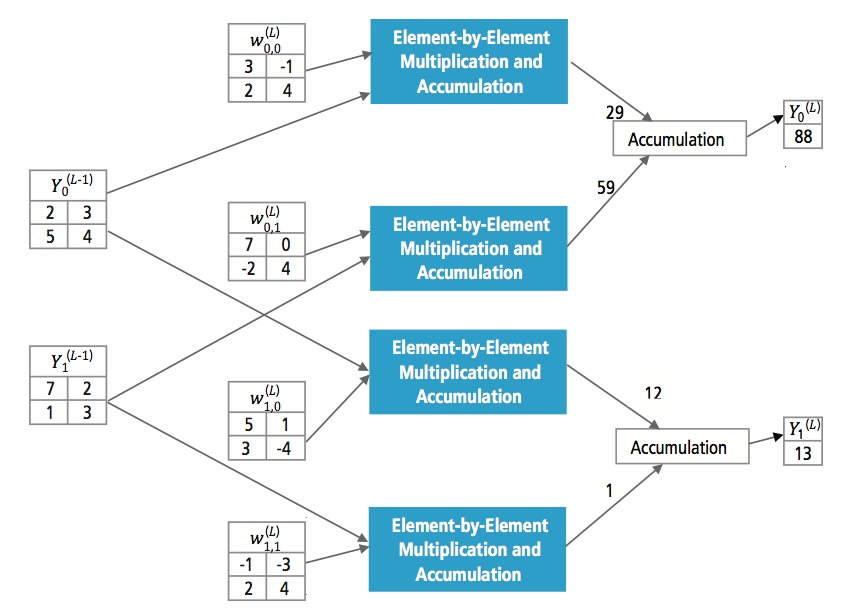
Abbildung 13: Verarbeitung einer vollverknüpften Schicht

Warum CNN?

Neuronale Netze und andere Methoden zur Mustererkennung gibt es zwar schon seit 50 Jahren, aber in jüngster Zeit hat sich das Gebiet der Faltungsneuronalen Netze erheblich weiterentwickelt. In diesem Abschnitt werden die Vorteile des Einsatzes von CNN für die Bilderkennung behandelt.

Robustheit gegenüber Verschiebungen und Verzerrungen im Bild

Die Erkennung mit CNN ist robust gegenüber Verzerrungen wie Formveränderungen durch die Kameralinse, unterschiedliche Beleuchtungsbedingungen, unterschiedliche Posen, Vorhandensein von Teilverdeckungen, horizontale und vertikale Verschiebungen usw. CNNs sind jedoch verschiebungsinvariant, da im gesamten Raum die gleiche Gewichtskonfiguration verwendet wird. Theoretisch können wir die Verschiebungsinvarianz auch mit vollständig verbundenen Schichten erreichen. Das Ergebnis des Trainings sind in diesem Fall jedoch mehrere Einheiten mit identischen Gewichtungsmustern an verschiedenen Stellen der Eingabe. Um diese Gewichtskonfigurationen zu erlernen, wäre eine große Anzahl von Trainingsinstanzen erforderlich, um den Raum möglicher Variationen abzudecken.

geringerer Speicherbedarf

In demselben hypothetischen Fall, in dem wir eine voll verknüpfte Schicht verwenden, um die Merkmale zu extrahieren, würde das Eingangsbild der Größe 32×32 und eine verborgene Schicht mit 1000 Merkmalen eine Größenordnung von 106 Koeffizienten erfordern, ein enormer Speicherbedarf. In der Faltungsschicht werden dieselben Koeffizienten an verschiedenen Stellen im Raum verwendet, so dass der Speicherbedarf drastisch reduziert wird.

Einfacheres und besseres Training

Bei der Verwendung eines normalen neuronalen Netzes, das einem CNN entsprechen würde, würde die Trainingszeit ebenfalls proportional ansteigen, da die Anzahl der Parameter viel höher wäre. Da bei einem CNN die Anzahl der Parameter drastisch reduziert wird, verringert sich die Trainingszeit entsprechend. Unter der Annahme eines perfekten Trainings können wir auch ein normales neuronales Netz entwerfen, dessen Leistung mit der eines CNN vergleichbar wäre. In der Praxis würde jedoch ein Standard-Neuronalnetz, das einem CNN entspricht, mehr Parameter haben, was zu mehr Rauschen während des Trainingsprozesses führen würde. Daher wird die Leistung eines neuronalen Standardnetzes, das einem CNN entspricht, immer schlechter sein.

Erkennungsalgorithmus für den GTSRB-Datensatz

Der German Traffic Sign Recognition Benchmark (GTSRB) war ein Mehrklassen-Einzelbild-Klassifikationswettbewerb auf der International Joint Conference on Neural Networks (IJCNN) 2011 mit folgenden Anforderungen:

• 51.840 Bilder von deutschen Verkehrsschildern in 43 Klassen (Abbildungen 14 und 15)
• Die Größe der Bilder variiert von 15×15 bis 222×193
• Die Bilder sind nach Klasse und Spur gruppiert, mit mindestens 30 Bildern pro Spur
• Die Bilder liegen als Farbbilder (RGB), HOG-Merkmale, Haar-Merkmale und Farbhistogramme vor
• Der Wettbewerb bezieht sich nur auf den Klassifikationsalgorithmus; Algorithmus zum Auffinden der interessierenden Region im Bild ist nicht erforderlich
• Die zeitlichen Informationen der Testsequenzen werden nicht gemeinsam genutzt, daher kann die zeitliche Dimension nicht im Klassifizierungsalgorithmus verwendet werden

Abbildung 14: Ideale GTSRB-Verkehrszeichen

Abbildung 15: GTSRB-Verkehrszeichen mit Beeinträchtigungen

Cadence-Algorithmus zur Verkehrszeichenerkennung im GTSRB-Datensatz

Cadence hat in MATLAB verschiedene Algorithmen zur Verkehrszeichenerkennung mit dem GTSRB-Datensatz entwickelt, beginnend mit einer Basiskonfiguration, die auf einer bekannten Arbeit zur Verkehrszeichenerkennung basiert. Die korrekte Erkennungsrate von 99,24 % und der Rechenaufwand von fast >50 Millionen Multiplikationsadditionen pro Schild sind in Abbildung 16 als dicker grüner Punkt dargestellt. Deutlich bessere Ergebnisse hat Cadence mit seinem neuen proprietären Hierarchical CNN-Ansatz erzielt. Bei diesem Algorithmus wurden 43 Verkehrszeichen in fünf Familien unterteilt. Insgesamt implementieren wir sechs kleinere CNNs. Das erste CNN entscheidet, zu welcher Familie das empfangene Verkehrszeichen gehört. Sobald die Familie des Zeichens bekannt ist, wird das CNN (eines der übrigen fünf), das der erkannten Familie entspricht, ausgeführt, um das Verkehrszeichen innerhalb dieser Familie zu bestimmen. Mit diesem Algorithmus hat Cadence eine korrekte Erkennungsrate von 99,58% erreicht, die beste CDR, die bisher auf GTSRB erreicht wurde.

Algorithmus für den Kompromiss zwischen Leistung und Komplexität

Um die Komplexität von CNNs in eingebetteten Anwendungen zu kontrollieren, hat Cadence auch einen proprietären Algorithmus entwickelt, der Eigenwert-Zerlegung verwendet und ein trainiertes CNN auf seine kanonische Dimension reduziert. Mit diesem Algorithmus konnten wir die Komplexität des CNN ohne Leistungseinbußen oder mit einer kleinen kontrollierten CDR-Reduktion drastisch reduzieren. Abbildung 16 zeigt die erzielten Ergebnisse:

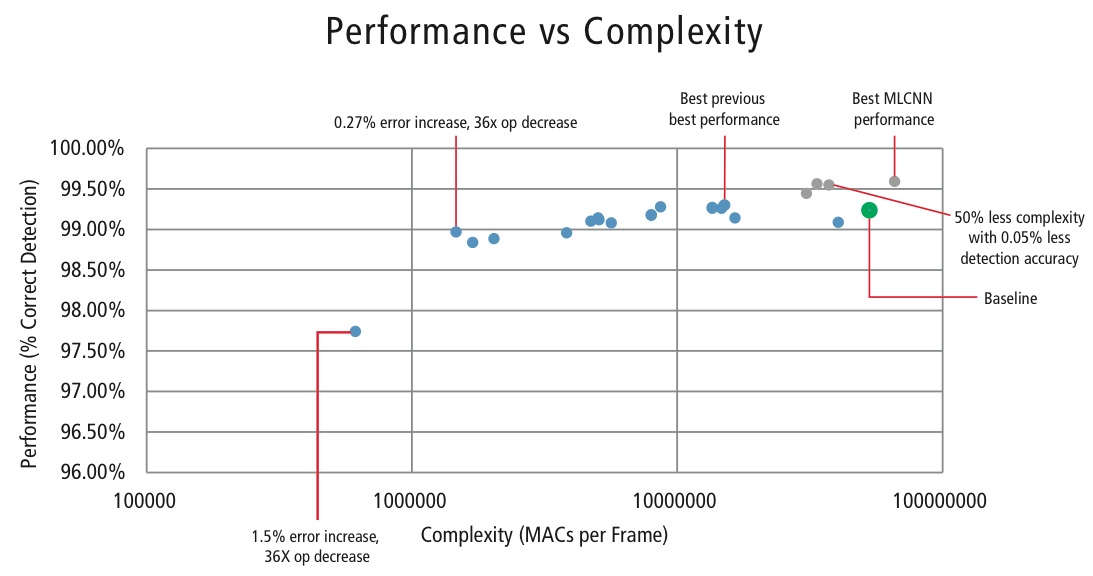
Abbildung 16: Leistung vs. Komplexität für verschiedene CNN-Konfigurationen zur Erkennung von Verkehrszeichen im GTSRB-Datensatz

Der grüne Punkt in Abbildung 16 ist die Basiskonfiguration. Diese Konfiguration kommt der in Referenz vorgeschlagenen Konfiguration recht nahe. Sie erfordert 53 MMACs pro Frame für eine Fehlerrate von 0,76%.

• Der zweite Punkt von links erfordert 1,47 Millionen MACs pro Frame für eine Fehlerrate von 1,03%, d.h., bei einer Erhöhung der Fehlerrate um 0,27 % verringert sich der MAC-Bedarf um den Faktor 36,14.
• Der Punkt ganz links benötigt 0,61 MMACs pro Frame, um eine Fehlerrate von 2,26 % zu erreichen, d. h. die Anzahl der MACs verringert sich um den Faktor 86,4.
• Die Punkte in blau gelten für ein einstufiges CNN, während die Punkte in rot für ein hierarchisches CNN gelten. Im besten Fall erreicht das hierarchische CNN eine Leistung von 99,58 %.

CNNs in eingebetteten Systemen

Wie aus Abbildung 5 hervorgeht, erfordert ein Bildverarbeitungs-Subsystem zusätzlich zu einem CNN eine Menge an Bildverarbeitung. Um CNNs auf einem eingebetteten System mit eingeschränktem Stromverbrauch zu betreiben, das die Bildverarbeitung unterstützt, sollte es die folgenden Anforderungen erfüllen:

• Verfügbarkeit einer hohen Rechenleistung: Für eine typische CNN-Implementierung sind Milliarden von MACs pro Sekunde erforderlich.
• Große Lade-/Speicher-Bandbreite: Im Falle einer vollständig verbundenen Schicht, die für Klassifizierungszwecke verwendet wird, wird jeder Koeffizient nur einmal bei der Multiplikation verwendet. Daher ist die erforderliche Load-Store-Bandbreite größer als die Anzahl der vom Prozessor durchgeführten MACs.
• geringer dynamischer Leistungsbedarf: Das System sollte weniger Strom verbrauchen. Um dieses Problem zu lösen, ist eine Festkomma-Implementierung erforderlich, bei der die Leistungsanforderungen mit einer möglichst geringen endlichen Anzahl von Bits erfüllt werden müssen.
• Flexibilität: Es sollte möglich sein, das bestehende Design leicht auf ein neues, leistungsfähigeres Design aufzurüsten.

Da Rechenressourcen in eingebetteten Systemen immer eine Einschränkung darstellen, ist es hilfreich, einen Algorithmus zu haben, der enorme Einsparungen bei der Rechenkomplexität auf Kosten einer kontrollierten, geringen Leistungsverschlechterung erzielen kann, wenn der Anwendungsfall eine kleine Leistungsverschlechterung erlaubt. Die Arbeit von Cadence an einem Algorithmus zur Erzielung eines Kompromisses zwischen Komplexität und Leistung, wie im vorherigen Abschnitt erläutert, ist daher von großer Bedeutung für die Implementierung von CNNs auf eingebetteten Systemen.

CNNs auf Tensilica-Prozessoren

Der Tensilica Vision P5 DSP ist ein hochleistungsfähiger DSP mit geringem Stromverbrauch, der speziell für die Bild- und Computer-Vision-Verarbeitung entwickelt wurde. Der DSP hat eine VLIW-Architektur mit SIMD-Unterstützung. Er verfügt über fünf Ausgabeslots in einem Befehlswort von bis zu 96 Bit und kann pro Zyklus bis zu 1024-Bit-Wörter aus dem Speicher laden. Interne Register und Operationseinheiten reichen von 512 Bits bis 1536 Bits, wobei die Daten als 16, 32 oder 64 Slices von 8b, 16b, 24b, 32b oder 48b Pixeldaten dargestellt werden.

Der DSP geht auf alle Herausforderungen bei der Implementierung von CNNs in eingebetteten Systemen ein, die im vorherigen Abschnitt erörtert wurden.

• Verfügbarkeit einer hohen Rechenleistung: Zusätzlich zur erweiterten Unterstützung für die Implementierung der Bildsignalverarbeitung verfügt der DSP über Befehlsunterstützung für alle Stufen von CNNs. Für Faltungsoperationen verfügt er über einen sehr umfangreichen Befehlssatz, der Multiplikations-/Multiplikations-/Akkumulationsoperationen mit 8b x 8b, 8b x 16b und 16b x 16b für Daten mit und ohne Vorzeichen unterstützt. Er kann bis zu 64 8b x 16b und 8b x 8b Multiplikations-/Multiplikations-/Akkumulationsoperationen in einem Zyklus und 32 16b x 16b Multiplikations-/Multiplikations-/Akkumulationsoperationen in einem Zyklus durchführen. Für die Max-Pooling- und ReLU-Funktionalität verfügt der DSP über Befehle zur Durchführung von 64 8-Bit-Vergleichen in einem Zyklus. Für die Implementierung nichtlinearer Funktionen mit endlichen Bereichen wie tanh und signum verfügt er über Anweisungen zur Implementierung einer Look-up-Tabelle für 64 7-Bit-Werte in einem Zyklus. In den meisten Fällen werden die Befehle für den Vergleich und die Nachschlagetabelle parallel zu den Multiplikations-/Multiplikations-/Akkumulationsbefehlen eingeplant und benötigen keine zusätzlichen Zyklen.
• Größere Lade-/Speicher-Bandbreite: Der DSP kann bis zu zwei 512-Bit-Lade-/Speicheroperationen pro Zyklus durchführen.
• Niedriger dynamischer Leistungsbedarf: Der DSP ist eine Festkomma-Maschine. Aufgrund der flexiblen Handhabung einer Vielzahl von Datentypen kann die volle Leistung und der Energievorteil einer gemischten 16b- und 8b-Berechnung bei minimalem Genauigkeitsverlust erreicht werden.
• Flexibilität: Da der DSP ein programmierbarer Prozessor ist, kann das System einfach durch ein Firmware-Upgrade auf eine neue Version aufgerüstet werden.
• Floating Point: Für Algorithmen, die einen erweiterten Dynamikbereich für ihre Daten und/oder Koeffizienten benötigen, verfügt der DSP über eine optionale Vektor-Gleitkommaeinheit.

Der Vision P5 DSP wird mit einem kompletten Satz von Software-Tools geliefert, der einen leistungsstarken C/C++-Compiler mit automatischer Vektorisierung und Scheduling zur Unterstützung der SIMD- und VLIW-Architektur umfasst, ohne dass Assembler geschrieben werden muss. Zu diesem umfassenden Toolset gehören auch Linker, Assembler, Debugger, Profiler und grafische Visualisierungswerkzeuge. Ein umfassender Befehlssatzsimulator (ISS) ermöglicht es dem Entwickler, die Leistung schnell zu simulieren und zu bewerten. Bei der Arbeit mit großen Systemen oder langen Testvektoren erreicht die schnelle, funktionale TurboXim-Simulator-Option Geschwindigkeiten, die 40- bis 80-mal schneller sind als der ISS für eine effiziente Software-Entwicklung und funktionale Verifikation.

Cadence hat auf dem DSP eine Single-Layer-Architektur CNN für die deutsche Verkehrszeichenerkennung implementiert. Cadence hat für diese Architektur eine CDR von 99,403% mit 16-Bit-Quantisierung für Daten-Samples und 8-Bit-Quantisierung für Koeffizienten in allen Schichten erreicht. Sie verfügt über zwei Faltungsschichten, drei voll verknüpfte Schichten, vier ReLU-Schichten, drei Max-Pooling-Schichten und eine nichtlineare tanh-Schicht. Cadence hat eine durchschnittliche Leistung von 38,58 MACs/Zyklus für das gesamte Netzwerk erreicht, einschließlich der Zyklen für alle Max-Pooling-, Tanh- und ReLU-Schichten. Cadence hat eine Best-Case-Leistung von 58,43 MACs pro Zyklus für die dritte Schicht erreicht, einschließlich der Zyklen für tanh- und ReLU-Funktionalitäten. Dieser DSP, der mit 600 MHz läuft, kann mehr als 850 Verkehrszeichen in einer Sekunde verarbeiten.

Die Zukunft der CNNs

Zu den vielversprechenden Bereichen der Forschung im Bereich der neuronalen Netze gehören rekurrente neuronale Netze (RNNs), die einen langen Kurzzeitspeicher (LSTM) verwenden. Diese Bereiche stellen den derzeitigen Stand der Technik bei der Erkennung von Zeitreihen wie Sprach- und Handschrifterkennung dar. RNN/Autocodierer sind auch in der Lage, Handschrift/Sprache/Bilder mit einer bekannten Verteilung zu erzeugen ,,,,.

Deep Belief Networks, ein weiterer vielversprechender Netzwerktyp, der Restricted Boltzman Machines (RMBs)/Autocodierer verwendet, können gierig trainiert werden, eine Schicht nach der anderen, und sind daher leichter für sehr tiefe Netze trainierbar.

Schlussfolgerung

CNNs erbringen die beste Leistung bei Problemen der Muster-/Bilderkennung und übertreffen in bestimmten Fällen sogar den Menschen. Cadence hat mit eigenen Algorithmen und Architekturen mit CNNs die besten Ergebnisse in der Branche erzielt. Wir haben hierarchische CNNs für die Erkennung von Verkehrsschildern in der GTSRB entwickelt und dabei die beste Leistung erzielt, die je in diesem Datensatz erzielt wurde. Wir haben einen weiteren Algorithmus für den Kompromiss zwischen Leistung und Komplexität entwickelt und konnten eine Komplexitätsreduktion um den Faktor 86 bei einer CDR-Verschlechterung von weniger als 2 % erreichen. Der Tensilica Vision P5 DSP für Bildverarbeitung und Computer Vision von Cadence verfügt über alle Funktionen, die für die Implementierung von CNNs erforderlich sind, zusätzlich zu den Funktionen, die für die Bildsignalverarbeitung benötigt werden. Mehr als 850 Verkehrszeichenerkennungen können mit dem DSP bei 600MHz durchgeführt werden. Der Tensilica Vision P5 DSP von Cadence verfügt über einen nahezu idealen Satz von Funktionen, um CNNs auszuführen.

„Künstliches neuronales Netzwerk.“ Wikipedia. https://en.wikipedia.org/wiki/Artificial_neural_network

Karpathy, Andrej. 2015. „Neural Networks Part 1: Setting Up the Architecture“. Notes for CS231n Convolutional Neural Networks for Visual Recognition, Stanford University. http://cs231n.github.io/neural-networks-1/

„Convolutional neural network.“ Wikipedia. https://en.wikipedia.org/wiki/Convolutional_neural_network

Sermanet, Pierre, und Yann LeCun. 2011. „Traffic Sign Recognition with Multi Scale Networks“. Courant Institute of Mathematical Sciences, New York University. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6033589

Ciresan, Dan, Ueli Meier, and Jürgen Schmidhuber. 2012. „Multi-column deep neural networks for image classi- fication“. 2012 IEEE Conference on Computer Vision and Pattern Recognition (New York, NY: Institute of Electrical and Electronics Engineers (IEEE)). http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6248110

Ciresan, Dan, Ueli Meier, Jonathan Masci, Luca M. Gambardella, and Jurgen Schmidhuber. 2011. „Flexible, High Performance Convolutional Neural Networks for Image Classification“. Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence-Volume Two: 1237-1242. Retrieved 17 November 2013. http://people.idsia.ch/~juergen/ijcai2011.pdf

Lawrence, Steve, C. Lee Giles, Ah Chung Tsoi, and Andrew D. Back. 1997. „Face Recognition: A Convolutional Neural Network Approach.“ IEEE Transactions on Neural Networks, Volume 8; Issue 1. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=554195

Russakovsky, O. et al. 2014. „ImageNet Large Scale Visual Recognition Challenge.“ International Journal of Computer Vision. http://link.springer.com/article/10.1007/s11263-015-0816-y#

Ovtcharov, Kalin, Olatunji Ruwarse, Joo-Young Kim et al. Feb 22, 2015. „Accelerating Deep Convolutional Networks Using Specialized Hardware“. Microsoft Research. http://research-srv.microsoft.com/pubs/240715/CNN%20Whitepaper.pdf

Stallkamp, J., M. Schlipsing, J. Salmen, and C. Igel. „Man Vs. Computer: Benchmarking Machine Learning Algorithms For Traffic Sign Application.“ IJCNN 2011. http://www.sciencedirect.com/science/article/pii/S0893608012000457

Hochreiter, Sepp, und Jürgen Schmidhuber. 1997. „Long Short-Term Memory.“ Neural Computation, 9(8):1735-1780. ftp://ftp.idsia.ch/pub/juergen/lstm.pdf

Graves, Alex. 2014. „Generating Sequences With Recurrent Neural Networks.“ http://arxiv.org/abs/1308.0850

Schmidhuber, Jurgen. 2015. „Recurrent Neural Networks.“ http://people.idsia.ch/~juergen/rnn.html

Olshausen, Bruno A., und David J. Field. 1996. „Emergenz von Eigenschaften des rezeptiven Feldes einfacher Zellen durch Lernen eines spärlichen Codes für natürliche Bilder“. Nature 381.6583: 607-609. http://www.nature.com/nature/journal/v381/n6583/abs/381607a0.html

Hinton, G. E. und Salakhutdinov, R. R. 2006. „Reducing the dimensionality of data with neural networks“. Science vol. 313 no. 5786 pp. 504-507. http://www.sciencemag.org/content/suppl/2006/08/04/313.5786.504.DC1.

Hinton, Geoffrey E. 2009. „Deep belief networks.“ Scholarpedia, 4(5):5947.
http://www.scholarpedia.org/article/Deep_belief_networks