Mediile mobile în pandas

Introducere
O medie mobilă, numită și medie mobilă sau medie de rulare, este utilizată pentru a analiza datele din seriile de timp prin calcularea mediilor diferitelor subseturi ale setului complet de date. Deoarece implică luarea mediei setului de date de-a lungul timpului, se mai numește și medie mobilă (MM) sau medie mobilă.
Există diverse moduri în care poate fi calculată media mobilă, dar unul dintre acestea este de a lua un subset fix dintr-o serie completă de numere. Prima medie mobilă este calculată prin calcularea mediei primului subset fix de numere, iar apoi subsetul este modificat prin trecerea la următorul subset fix (incluzând valoarea viitoare în subgrup, excluzând în același timp numărul anterior din serie).
Media mobilă este utilizată în principal cu date din serii de timp pentru a surprinde fluctuațiile pe termen scurt, concentrându-se în același timp pe tendințele mai lungi.
Câteva exemple de date din serii temporale pot fi prețurile acțiunilor, rapoartele meteo, calitatea aerului, produsul intern brut, ocuparea forței de muncă etc.
În general, media mobilă netezește datele.
Media mobilă este coloana vertebrală a multor algoritmi, iar un astfel de algoritm este Autoregressive Integrated Moving Average Model (ARIMA), care folosește mediile mobile pentru a face predicții ale datelor din seriile de timp.
Există diferite tipuri de medii mobile:
Simple Moving Average (SMA): Media mobilă simplă (SMA) utilizează o fereastră glisantă pentru a lua media pe un număr stabilit de perioade de timp. Este o medie cu pondere egală a celor n date anterioare.
Pentru a înțelege mai bine SMA, să luăm un exemplu, o secvență de n valori:

atunci media mobilă egal ponderată pentru n puncte de date va fi, în esență, media celor M puncte de date anterioare, unde M este dimensiunea ferestrei glisante:

În mod similar, pentru calcularea valorilor medii mobile succesive, o nouă valoare va fi adăugată la sumă, iar valoarea perioadei de timp anterioare va fi eliminată, deoarece aveți media perioadelor de timp anterioare, astfel încât nu este necesară o însumare completă de fiecare dată:

- Cumulative Moving Average (CMA): Spre deosebire de media mobilă simplă, care elimină cea mai veche observație pe măsură ce se adaugă una nouă, media mobilă cumulativă ia în considerare toate observațiile anterioare. CMA nu este o tehnică foarte bună pentru analiza tendințelor și pentru netezirea datelor. Motivul este că face o medie a tuturor datelor anterioare până la punctul de date curent, deci o medie cu pondere egală a secvenței de n valori:



- Exponential Moving Average (EMA): Spre deosebire de SMA și CMA, media mobilă exponențială acordă o pondere mai mare prețurilor recente și, ca urmare, poate fi un model mai bun sau poate surprinde mai bine mișcarea tendinței într-un mod mai rapid. Reacția EMA este direct proporțională cu modelul datelor.
Din moment ce EMA acordă o pondere mai mare datelor recente decât datelor mai vechi, ele sunt mai receptive la cele mai recente schimbări de preț în comparație cu SMA, ceea ce face ca rezultatele obținute de EMA să fie mai oportune și, prin urmare, EMA este mai preferată decât alte tehnici.
Suficient cu teoria, nu? Să trecem la implementarea practică a mediei mobile.
Implementarea mediei mobile pe date din serii de timp
Simple Moving Average (SMA)
În primul rând, haideți să creăm date fictive din serii de timp și să încercăm să implementăm SMA folosind doar Python.
Să presupunem că există o cerere pentru un produs și că aceasta este observată timp de 12 luni (1 an) și că trebuie să găsiți medii mobile pentru perioadele de fereastră de 3 și 4 luni.
Modul de import
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| lună | demanda | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Să calculăm SMA pentru o dimensiune a ferestrei de 3, ceea ce înseamnă că veți lua în considerare de fiecare dată trei valori pentru a calcula media mobilă, iar pentru fiecare valoare nouă, cea mai veche valoare va fi ignorată.
Pentru a implementa acest lucru, veți folosi funcția pandas iloc, deoarece coloana demand este cea de care aveți nevoie, veți fixa poziția acesteia în funcția iloc, în timp ce rândul va fi o variabilă i pe care o veți continua să o iterați până când veți ajunge la sfârșitul cadrului de date.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| lună | demand | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Pentru o verificare a corectitudinii, să folosim, de asemenea, funcția pandas încorporată rolling și să vedem dacă aceasta se potrivește cu media mobilă simplă personalizată bazată pe python.
df = df.iloc.rolling(window=3).mean()df.head()| lună | demanda | SMA_3 | pandas_SMA_3 | ||
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | |
| 3 | 4 | 300 | 282.7 | 282.666667 | |
| 4 | 5 | 310 | 299.3 | 299.33333333 |
Cool, deci, după cum puteți vedea, mediile mobile personalizate și pandas se potrivesc exact, ceea ce înseamnă că implementarea SMA a fost corectă.
Să calculăm rapid și media mobilă simplă pentru un window_size de 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| lună | demanda | SMA_3 | pandas_SMA_3 | SMA_4 | ||
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | |
| 1 | 2 | 260 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| lună | demandă | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | ||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.33333333 | NaN | NaN | |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.33333333 | 289.5 | 289.5 |
Acum, veți reprezenta grafic datele mediilor mobile pe care le-ați calculat.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>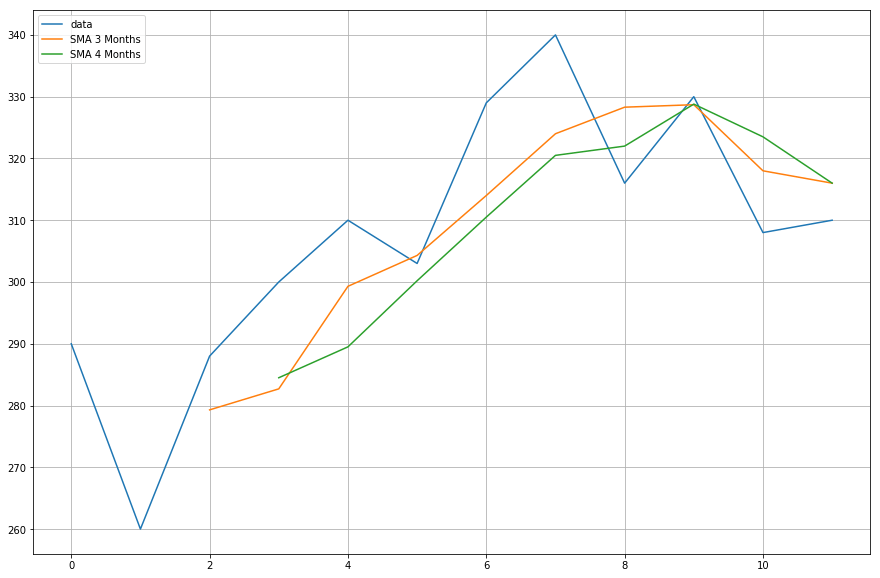
Media mobilă cumulativă
Cred că acum suntem pregătiți să trecem la un set de date reale.
Pentru media mobilă cumulativă, să folosim un air quality dataset care poate fi descărcat de la acest link.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Prelucrarea este un pas esențial ori de câte ori se lucrează cu date. Pentru datele numerice, una dintre cele mai frecvente etape de preprocesare este verificarea valorilor NaN (Null). Dacă există valori NaN, le puteți înlocui fie cu 0, fie cu valori medii, fie cu valori precedente sau succesive, fie chiar le puteți elimina. Deși înlocuirea este în mod normal o alegere mai bună decât renunțarea la ele, deoarece acest set de date are puține valori NULL, renunțarea la ele nu va afecta continuitatea seriei.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Din rezultatul de mai sus, puteți observa că există în jur de 114 valori NaN pe toate coloanele, însă vă veți da seama că toate se află la sfârșitul seriei de timp, așa că haideți să le renunțăm rapid.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Vă veți aplica media mobilă cumulativă pe Temperature column (T), așa că haideți să separăm rapid această coloană din datele complete.
df_T = pd.DataFrame(df.iloc)df_T.head()
Acum, veți utiliza metoda pandas expanding pentru a găsi media cumulată a datelor de mai sus. Dacă vă amintiți din introducere, spre deosebire de media mobilă simplă, media mobilă cumulativă ia în considerare toate valorile precedente atunci când calculează media.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Datele din seriile temporale sunt reprezentate grafic în funcție de timp, așa că haideți să combinăm coloana de dată și oră și să o convertim într-un obiect datetime. Pentru a realiza acest lucru, veți utiliza modulul datetime din python (Sursa: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Să schimbăm indicele din dataframe-ul temperature cu datatime.
df_T.index = df.DateTimeSă reprezentăm acum temperatura reală și media mobilă cumulativă în raport cu timpul.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Media mobilă exponențială
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |||
|---|---|---|---|---|---|
| DateTime | |||||
| 2004…03-10 18:00:00 | 13.6 | NaN | 13.600000 | ||
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 | ||
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.585366 | ||
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 | ||
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | ||
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>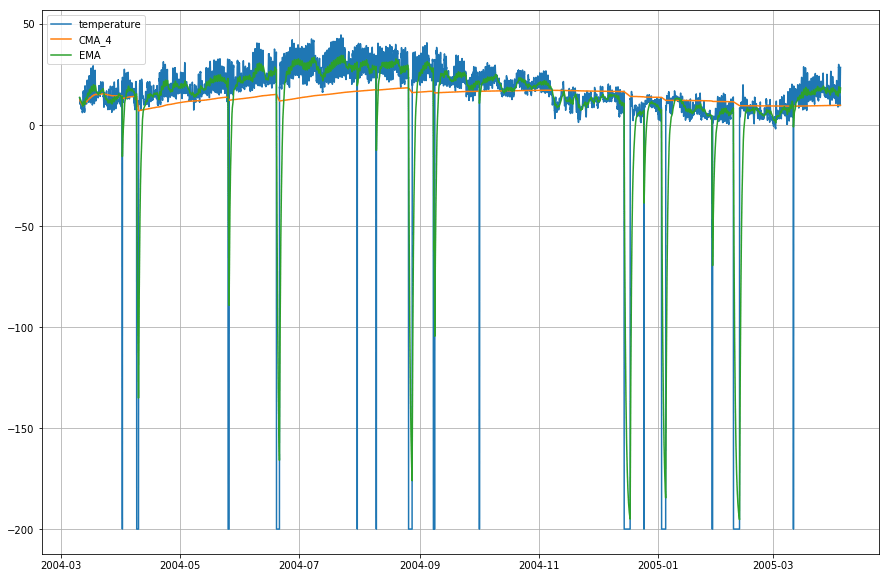
Wow! Deci, după cum puteți observa din graficul de mai sus, că Exponential Moving Average (EMA) face o treabă superbă în captarea modelului de date, în timp ce Cumulative Moving Average (CMA) lipsește cu o marjă considerabilă.
Vă mai departe!
Felicitări pentru terminarea tutorialului.
Acest tutorial a fost un bun punct de plecare în ceea ce privește modul în care puteți calcula mediile mobile ale datelor dvs. și să le dați un sens.
Încercați să scrieți codul python al mediilor mobile cumulative și exponențiale fără a utiliza biblioteca pandas. Acest lucru vă va oferi cunoștințe mult mai aprofundate despre modul în care sunt calculate și în ce fel sunt ele diferite una de cealaltă.
Există încă multe de experimentat. Încercați să calculați autocorelația parțială între datele de intrare și media mobilă și încercați să găsiți o relație între cele două.
Dacă doriți să aflați mai multe despre DataFrames în pandas, urmați cursul interactiv Pandas Foundations de la DataCamp.
.