De-Multiplexorul este un circuit combinațional care realizează operația inversă a Multiplexorului. Acesta are o singură intrare, „n” linii de selecție și maximum 2n ieșiri. Intrarea va fi conectată la una dintre aceste ieșiri în funcție de valorile liniilor de selecție.

Din moment ce există „n” linii de selecție, vor exista 2n combinații posibile de zerouri și unu. Deci, fiecare combinație poate selecta doar o singură ieșire. De-Multiplexorul se mai numește și De-Mux.

1×4 De-Multiplexor

1×4 De-Multiplexor are o intrare I, două linii de selecție, s1 & s0 și patru ieșiri Y3, Y2, Y1 &Y0. Schema bloc a De-Multiplexorului 1×4 este prezentată în figura următoare.

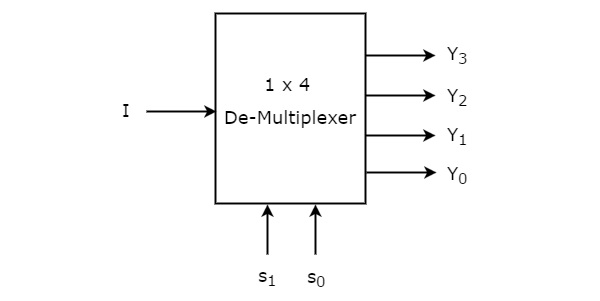
Una singură intrare „I” va fi conectată la una dintre cele patru ieșiri, Y3 până la Y0, pe baza valorilor liniilor de selecție s1 & s0. Tabelul de adevăr al de-multiplexorului 1×4 este prezentat mai jos.

.

.

.

Intrare de selecție		Salite
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	I
0	0	1	0	0	I	0
1	0	0	0	I	0	0	I	0	0
1	1	I	0	0	0	0	0

Din tabelul de adevăr de mai sus, putem scrie direct funcțiile booleene pentru fiecare ieșire sub forma

$$Y_{3}=s_{1}s_{0}I$$$

$Y_{2}=s_{1}{s_{0}}’I$$

$$Y_{1}={s_{1}}’s_{0}I$$

$Y_{0}={s_1}'{s_{0}}’I$

Potem implementa aceste funcții booleene folosind invertoarele & 3-porți AND de intrare. Schema de circuit a De-Multiplexorului 1×4 este prezentată în figura următoare.

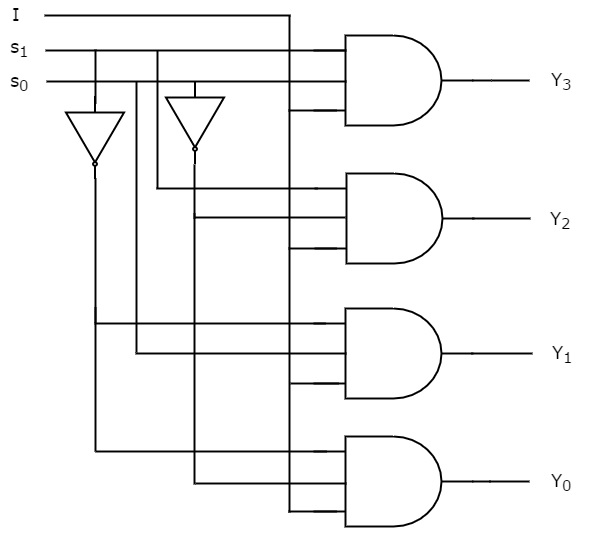
Potem înțelege cu ușurință funcționarea circuitului de mai sus. În mod similar, puteți implementa De-Multiplexorul 1×8 și De-Multiplexorul 1×16 urmând aceeași procedură.

Implementarea De-Multiplexoarelor de ordin superior

Acum, să implementăm următoarele două De-Multiplexoare de ordin superior folosind De-Multiplexoare de ordin inferior.

• 1×8 De-Multiplexor
• 1×16 De-Multiplexor

1×8 De-Multiplexor

În această secțiune, să implementăm 1×8 De-Multiplexor folosind 1×4 De-Multiplexor și 1×2 De-Multiplexor. Știm că 1×4 De-Multiplexor are o singură intrare, două linii de selecție și patru ieșiri. În timp ce De-Multiplexorul 1×8 are o singură intrare, trei linii de selecție și opt ieșiri.

Prin urmare, avem nevoie de două De-Multiplexoare 1×4 în a doua etapă pentru a obține cele opt ieșiri finale. Deoarece numărul de intrări în a doua etapă este de două, avem nevoie de un DeMultiplexor 1×2 în prima etapă, astfel încât ieșirile din prima etapă să fie intrările din a doua etapă. Intrarea acestui De-Multiplexor 1×2 va fi intrarea totală a De-Multiplexorului 1×8.

După ce De-Multiplexorul 1×8 are o intrare I, trei linii de selecție s2, s1 & s0 și ieșirile de la Y7 la Y0. Tabelul de adevăr al De-Multiplexorului 1×8 este prezentat mai jos.

.

.

.

Intrare de selecție			Salite
s2	s1	s0	Y7	Y6	Y5	Y4	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0	0

Putem implementa 1×8 De-Multiplexor folosind Multiplexoare de ordin inferior cu ușurință luând în considerare tabelul de adevăr de mai sus. Schema bloc a De-Multiplexorului 1×8 este prezentată în figura următoare.

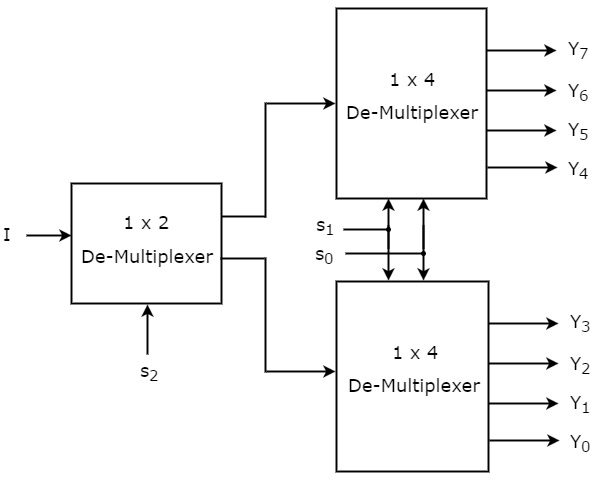
Liniile de selecție comune, s1 & s0 sunt aplicate la ambele De-Multiplexoare 1×4. Ieșirile De-Multiplexorului 1×4 superior sunt de la Y7 la Y4, iar ieșirile De-Multiplexorului 1×4 inferior sunt de la Y3 la Y0.

Celealaltă linie de selecție, s2 este aplicată De-Multiplexorului 1×2. Dacă s2 este zero, atunci una dintre cele patru ieșiri ale De-Multiplexorului 1×4 inferior va fi egală cu intrarea, I, pe baza valorilor liniilor de selecție s1 & s0. În mod similar, dacă s2 este unu, atunci una dintre cele patru ieșiri ale DeMultiplexorului 1×4 superior va fi egală cu intrarea I, pe baza valorilor liniilor de selecție s1 & s0.

De-Multiplexor 1×16

În această secțiune, să implementăm De-Multiplexorul 1×16 folosind De-Multiplexoare 1×8 și De-Multiplexorul 1×2. Știm că 1×8 De-Multiplexor are o singură intrare, trei linii de selecție și opt ieșiri. În timp ce 1×16 De-Multiplexor are o singură intrare, patru linii de selecție și șaisprezece ieșiri.

Deci, avem nevoie de două De-Multiplexoare 1×8 în a doua etapă pentru a obține șaisprezece ieșiri finale. Deoarece numărul de intrări în a doua etapă este de două, avem nevoie de un DeMultiplexor 1×2 în prima etapă, astfel încât ieșirile din prima etapă să fie intrările din a doua etapă. Intrarea acestui De-Multiplexor 1×2 va fi intrarea totală a De-Multiplexorului 1×16.

După ce De-Multiplexorul 1×16 are o intrare I, patru linii de selecție s3, s2, s1 & s0 și ieșirile Y15 până la Y0. Schema bloc a De-Multiplexorului 1×16 folosind Multiplexoare de ordin inferior este prezentată în figura următoare.

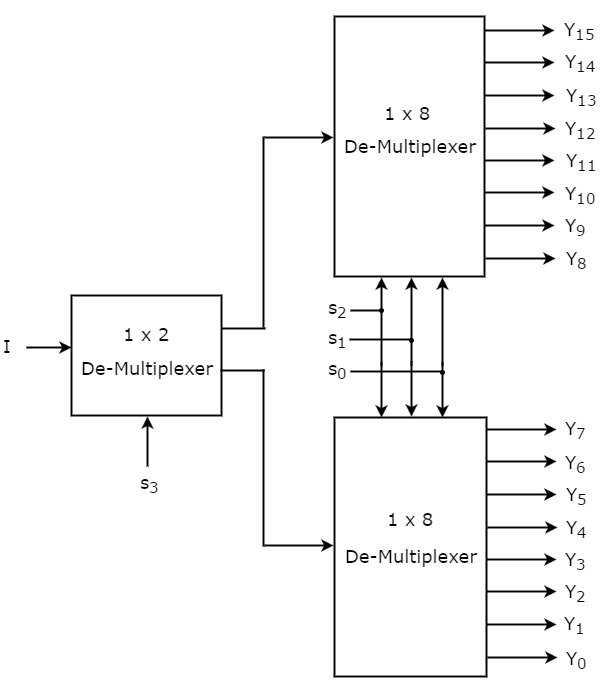
Liniile de selecție comune s2, s1 & s0 sunt aplicate la ambele De-Multiplexoare 1×8. Ieșirile De-Multiplexorului 1×8 superior sunt de la Y15 la Y8, iar ieșirile DeMultiplexorului 1×8 inferior sunt de la Y7 la Y0.

Celealaltă linie de selecție, s3, este aplicată la De-Multiplexorul 1×2. Dacă s3 este zero, atunci una dintre cele opt ieșiri ale De-Multiplexorului 1×8 inferior va fi egală cu intrarea, I pe baza valorilor liniilor de selecție s2, s1 & s0. În mod similar, dacă s3 este unu, atunci una dintre cele 8 ieșiri ale De-Multiplexorului 1×8 superior va fi egală cu intrarea, I pe baza valorilor liniilor de selecție s2, s1 & s0.

.