De-Multiplekser jest układem kombinacyjnym, który wykonuje operację odwrotną do multipleksera. Posiada pojedyncze wejście, 'n’ linii wyboru i maksymalnie 2n wyjść. Wejście zostanie podłączone do jednego z tych wyjść na podstawie wartości linii wyboru.

Ponieważ istnieje 'n’ linii wyboru, będzie 2n możliwych kombinacji zer i jedynek. Tak więc, każda kombinacja może wybrać tylko jedno wyjście. De-Multiplekser jest również nazywany De-Mux.

1×4 De-Multiplexer

1×4 De-Multiplexer ma jedno wejście I, dwie linie wyboru, s1 & s0 i cztery wyjścia Y3, Y2, Y1 &Y0. Schemat blokowy 1×4 De-Multipleksera jest pokazany na poniższym rysunku.

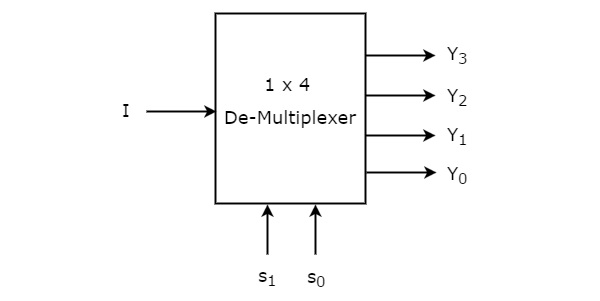
Pojedyncze wejście 'I’ będzie połączone z jednym z czterech wyjść, Y3 do Y0 na podstawie wartości linii wyboru s1 & s0. Tablica prawdy dla 1×4 De-Multiplexer jest pokazana poniżej.

.

.

.

Wejścia selekcji		Wyjścia
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	I
0	0	1	0	0	I	0
1	0	0	I	0	0	0
1	1	I	0	0	0

Z powyższej tabeli prawd, możemy bezpośrednio zapisać funkcje Boole’a dla każdego wyjścia jako

$$Y_{3}=s_{1}s_{0}I$$

$$Y_{2}=s_{1}{s_{0}}’I$$

$$Y_{1}={s_{1}}’s_{0}I$$

$$Y_{0}={s_{1}'{s_{0}}’I$$

Powyższe funkcje boolowskie możemy zaimplementować za pomocą inwerterów & 3-.3-wejściowych bramek AND. Schemat obwodu 1×4 De-Multiplexer jest pokazany na poniższym rysunku.

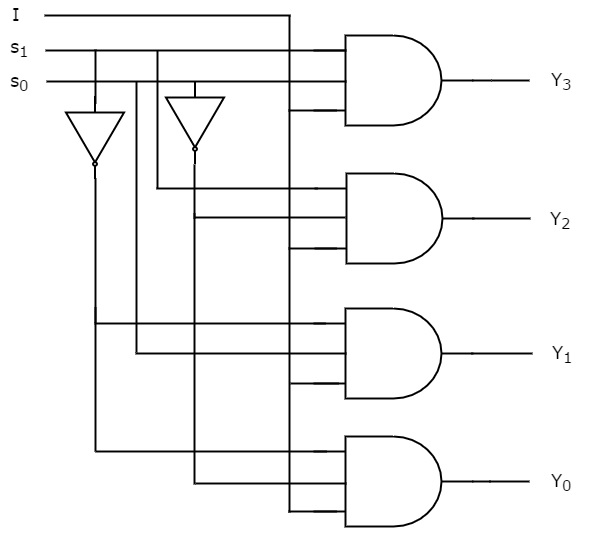
Możemy łatwo zrozumieć działanie powyższego obwodu. Podobnie, można zaimplementować De-Multiplekser 1×8 i De-Multiplekser 1×16 postępując według tej samej procedury.

Implementacja De-Multiplekserów wyższego rzędu

Zaimplementujmy teraz następujące dwa De-Multipleksery wyższego rzędu używając De-Multiplekserów niższego rzędu.

• 1×8 De-Multiplexer
• 1×16 De-Multiplexer

1×8 De-Multiplexer

W tej sekcji zaimplementujmy 1×8 De-Multiplexer używając 1×4 De-Multiplexer i 1×2 De-Multiplexer. Wiemy, że 1×4 De-Multiplexer ma jedno wejście, dwie linie wyboru i cztery wyjścia. Natomiast 1×8 De-Multiplexer ma pojedyncze wejście, trzy linie wyboru i osiem wyjść.

Więc potrzebujemy dwóch 1×4 De-Multiplexerów w drugim etapie, aby uzyskać końcowe osiem wyjść. Ponieważ liczba wejść w drugim stopniu wynosi dwa, potrzebujemy DeMultipleksera 1×2 w pierwszym stopniu, tak aby wyjścia pierwszego stopnia były wejściami drugiego stopnia. Wejście tego 1×2 De-Multiplexer będzie całkowitym wejściem 1×8 De-Multiplexer.

Let the 1×8 De-Multiplexer has one input I, three selection lines s2, s1 & s0 and outputs Y7 to Y0. Tabela prawdy dla 1×8 De-Multipleksera jest pokazana poniżej.

.

.

Wejścia selekcyjne			Wyjścia
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

Możemy zaimplementować 1×8 De-Multiplekser wykorzystujący Multipleksery niższego rzędu możemy łatwo zaimplementować biorąc pod uwagę powyższą tabelę prawdy. Schemat blokowy 1×8 De-Multipleksera jest pokazany na poniższym rysunku.

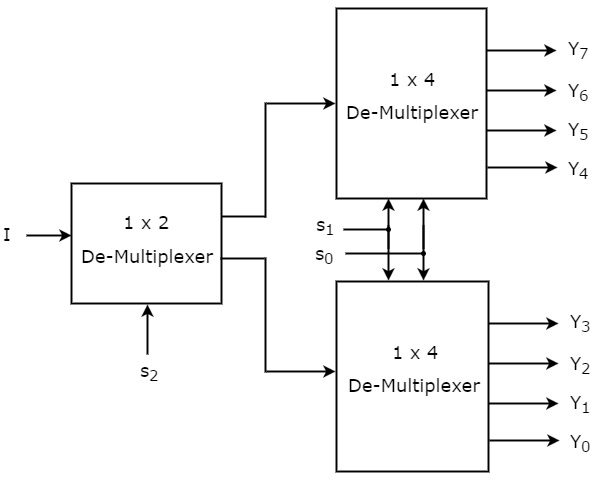
Wspólne linie wyboru, s1 & s0 są stosowane do obu 1×4 De-Multiplekserów. Wyjścia górnego multipleksera 1×4 to Y7 do Y4, a wyjścia dolnego multipleksera 1×4 to Y3 do Y0.

Inna linia wyboru, s2 jest stosowana do multipleksera 1×2. Jeśli s2 jest zerem, to jedno z czterech wyjść dolnego 1×4 De-Multiplexer będzie równe wejściu, I w oparciu o wartości linii selekcyjnych s1 & s0. Podobnie, jeśli s2 jest jeden, to jedno z czterech wyjść górnego 1×4 DeMultiplexer będzie równe wejściu, I na podstawie wartości linii wyboru s1 & s0.

1×16 De-Multiplexer

W tym rozdziale zaimplementujmy 1×16 De-Multiplexer używając 1×8 De-Multiplexers i 1×2 De-Multiplexer. Wiemy, że 1×8 De-Multiplexer ma jedno wejście, trzy linie wyboru i osiem wyjść. Natomiast 1×16 De-Multiplexer ma pojedyncze wejście, cztery linie wyboru i szesnaście wyjść.

Więc potrzebujemy dwóch 1×8 De-Multiplexerów w drugim etapie, aby uzyskać końcowe szesnaście wyjść. Ponieważ liczba wejść w drugim stopniu wynosi dwa, potrzebujemy DeMultipleksera 1×2 w pierwszym stopniu, tak aby wyjścia z pierwszego stopnia były wejściami drugiego stopnia. Wejście tego 1×2 De-Multiplexer będzie ogólnym wejściem 1×16 De-Multiplexer.

Let the 1×16 De-Multiplexer has one input I, four selection lines s3, s2, s1 & s0 and outputs Y15 to Y0. Schemat blokowy 1×16 De-Multiplexera wykorzystującego Multipleksery niższego rzędu jest pokazany na poniższym rysunku.

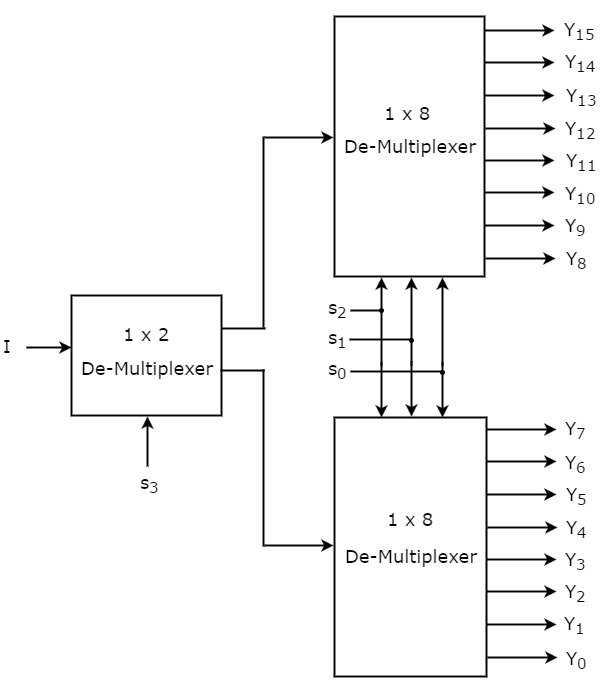
Wspólne linie selekcji s2, s1 & s0 są zastosowane do obu 1×8 De-Multiplexerów. Wyjścia górnego 1×8 demultipleksera to Y15 do Y8, a wyjścia dolnego 1×8 demultipleksera to Y7 do Y0.

Inna linia wyboru, s3 jest stosowana do 1×2 De-Multipleksera. Jeśli s3 jest zerem, to jedno z ośmiu wyjść niższego 1×8 De-Multipleksera będzie równe wejściu, I na podstawie wartości linii wyboru s2, s1 & s0. Podobnie, jeśli s3 jest jedynką, to jedno z 8 wyjść górnego 1×8 De-Multiplexera będzie równe wejściu, I na podstawie wartości linii wyboru s2, s1 & s0.

.