Średnie ruchome w pandach

Wprowadzenie
Średnia ruchoma, zwana również średnią kroczącą lub bieżącą, jest używana do analizy danych szeregu czasowego przez obliczanie średnich z różnych podzbiorów kompletnego zbioru danych. Ponieważ obejmuje to biorąc średnią zbioru danych w czasie, jest również nazywany średnią ruchomą (MM) lub rolling mean.
Są różne sposoby, w jaki średnia krocząca może być obliczona, ale jeden taki sposób jest wziąć stały podzbiór z pełnej serii liczb. Pierwsza średnia krocząca jest obliczana przez uśrednienie pierwszego ustalonego podzbioru liczb, a następnie podzbiór jest zmieniany przez przejście do następnego ustalonego podzbioru (włączając przyszłą wartość do podgrupy przy jednoczesnym wykluczeniu poprzedniej liczby z serii).
Średnia krocząca jest najczęściej używana z danymi szeregów czasowych w celu uchwycenia krótkoterminowych wahań przy jednoczesnym skupieniu się na dłuższych trendach.
Kilka przykładów danych szeregów czasowych mogą być ceny akcji, raporty pogodowe, jakość powietrza, produkt krajowy brutto, zatrudnienie, itp.
Ogólnie, średnia ruchoma wygładza dane.
Średnia ruchoma jest podstawą wielu algorytmów, a jednym z takich algorytmów jest Autoregressive Integrated Moving Average Model (ARIMA), który wykorzystuje średnie ruchome do prognozowania danych szeregów czasowych.
Są różne rodzaje średnich ruchomych:
-
Simple Moving Average (SMA): Simple Moving Average (SMA) wykorzystuje przesuwane okno, aby wziąć średnią z ustalonej liczby okresów czasu. Jest to równo ważona średnia z poprzednich n danych.
Aby zrozumieć SMA dalej, weźmy przykład, sekwencję n wartości:

to równo ważona średnia krocząca dla n punktów danych będzie zasadniczo średnią poprzednich M punktów danych, gdzie M jest rozmiarem okna przesuwnego:

Podobnie, przy obliczaniu kolejnych wartości średniej kroczącej, nowa wartość zostanie dodana do sumy, a wartość z poprzedniego okresu czasu zostanie pominięta, ponieważ mamy średnią z poprzednich okresów czasu, więc pełne sumowanie za każdym razem nie jest wymagane:

- Skumulowana średnia krocząca (CMA): W przeciwieństwie do prostej średniej kroczącej, która porzuca najstarszą obserwację w miarę dodawania nowej, kumulatywna średnia krocząca uwzględnia wszystkie wcześniejsze obserwacje. CMA nie jest bardzo dobrą techniką do analizy trendów i wygładzania danych. Powodem jest to, że uśrednia ona wszystkie poprzednie dane aż do bieżącego punktu danych, a więc równo ważoną średnią z ciągu n wartości:



- Wykładnicza średnia krocząca (EMA): W przeciwieństwie do SMA i CMA, wykładnicza średnia krocząca daje większą wagę do ostatnich cen, w wyniku czego może być lepszym modelem lub lepiej uchwycić ruch trendu w szybszy sposób. Reakcja EMA jest wprost proporcjonalna do wzorca danych.
Ponieważ EMA nadają większą wagę ostatnim danym niż starszym, są one bardziej wrażliwe na najnowsze zmiany cen w porównaniu do SMA, co sprawia, że wyniki z EMA są bardziej na czasie i dlatego EMA jest bardziej preferowana niż inne techniki.
Dość teorii, prawda? Przejdźmy do praktycznej implementacji średniej kroczącej.
Implementing Moving Average on Time Series Data
Simple Moving Average (SMA)
Po pierwsze, stwórzmy fikcyjne dane szeregu czasowego i spróbujmy zaimplementować SMA używając tylko Pythona.
Załóżmy, że istnieje popyt na produkt i jest on obserwowany przez 12 miesięcy (1 rok), i trzeba znaleźć średnie kroczące dla 3 i 4 miesięcznych okresów okna.
Moduł importu
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| miesiąc | demand | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Obliczmy SMA dla okna o rozmiarze 3, co oznacza, że za każdym razem do obliczenia średniej kroczącej będą brane pod uwagę trzy wartości, a dla każdej nowej wartości najstarsza wartość będzie ignorowana.
Aby to zaimplementować, użyjesz funkcji pandas iloc, ponieważ kolumna demand jest tym, czego potrzebujesz, ustalisz jej pozycję w funkcji iloc, podczas gdy wiersz będzie zmienną i, którą będziesz iterował, dopóki nie osiągniesz końca ramki danych.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| month | demand | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Dla sprawdzenia poprawności, użyjmy również pandas wbudowanej rolling funkcji i zobaczmy, czy pasuje ona do naszej niestandardowej prostej średniej kroczącej opartej na Pythonie.
df = df.iloc.rolling(window=3).mean()df.head()| month | demand | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, więc jak widzisz, niestandardowe i pandasowe średnie kroczące pasują dokładnie, co oznacza, że twoja implementacja SMA była poprawna.
Obliczmy też szybko prostą średnią kroczącą dla window_size równej 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| miesiąc | popyt | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| miesiąc | popyt | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299,333333 | 289,5 | 289,5 |
Teraz wykreślisz dane obliczonych średnich ruchomych.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>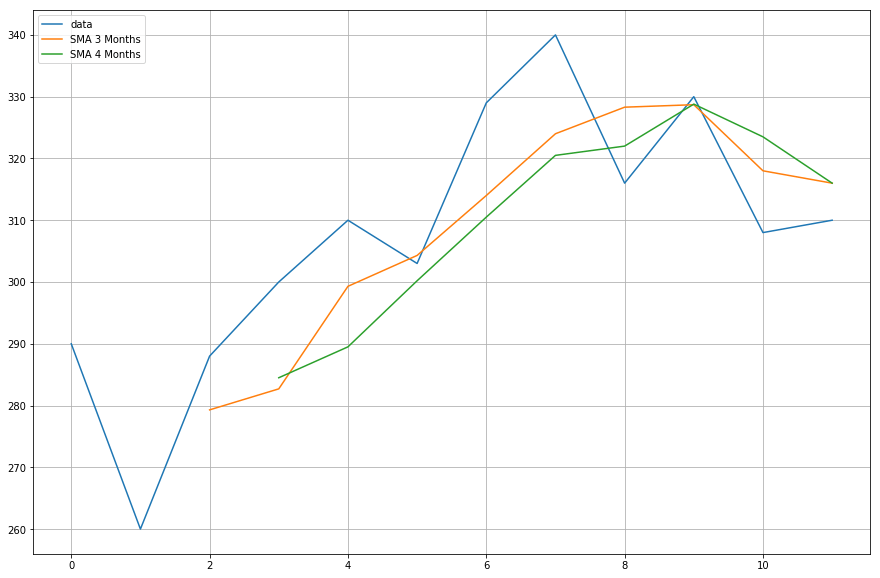
Skumulowana średnia krocząca
Sądzę, że teraz jesteśmy gotowi, aby przejść do prawdziwego zbioru danych.
Dla skumulowanej średniej kroczącej użyjmy modelu air quality dataset, który można pobrać z tego linku.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Data | Czas | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Preprocessing jest niezbędnym krokiem podczas pracy z danymi. W przypadku danych liczbowych jednym z najczęstszych kroków przetwarzania wstępnego jest sprawdzenie, czy nie występują wartości NaN (Null). Jeśli są jakieś NaN wartości, możesz zastąpić je albo 0 lub średnią lub poprzedzającymi lub następującymi wartościami lub nawet je porzucić. Chociaż zastąpienie jest zwykle lepszym wyborem niż upuszczenie ich, ponieważ ten zbiór danych ma niewiele wartości NULL, upuszczenie ich nie wpłynie na ciągłość serii.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Z powyższego wyjścia można zauważyć, że istnieje około 114 wartości NaN we wszystkich kolumnach, jednak dowiesz się, że wszystkie są na końcu serii czasowej, więc szybko je upuśćmy.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Będziesz stosować skumulowaną średnią kroczącą na Temperature column (T), więc szybko oddzielmy tę kolumnę od pełnych danych.
df_T = pd.DataFrame(df.iloc)df_T.head()
Teraz, użyjemy metody pandas expanding do znalezienia średniej skumulowanej z powyższych danych. Jeśli pamiętasz ze wstępu, w przeciwieństwie do prostej średniej ruchomej, skumulowana średnia ruchoma uwzględnia wszystkie poprzednie wartości podczas obliczania średniej.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Dane szeregu czasowego są wykreślane względem czasu, dlatego połączmy kolumnę daty i czasu i przekształćmy je w obiekt datetime. Aby to osiągnąć, użyjemy modułu datetime z pythona (Źródło: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Zmieńmy indeks ramki danych temperature z datetime.
df_T.index = df.DateTimeWykreślmy teraz temperaturę rzeczywistą i skumulowaną średnią ruchomą wrt. czasu.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponential Moving Average
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DateTime | |||
| 2004-.03-10 18:00:00 | 13.6 | NaN | 13.600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>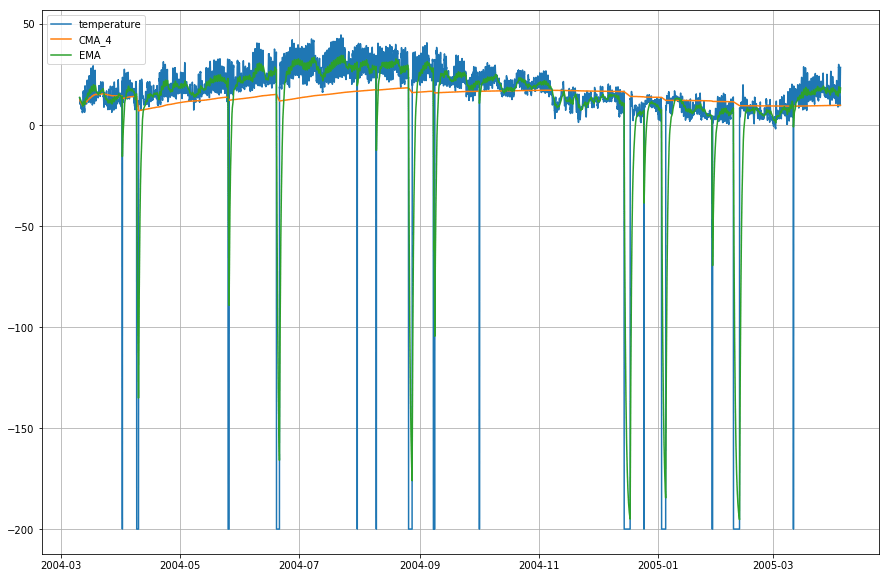
Wow! Jak więc można zauważyć na powyższym wykresie, Exponential Moving Average (EMA) wykonuje doskonałą pracę w przechwytywaniu wzorca danych, podczas gdy Cumulative Moving Average (CMA) brakuje mu znacznego marginesu.
Dalej!
Gratuluję ukończenia samouczka.
Ten samouczek był dobrym punktem wyjścia do tego, jak możesz obliczyć średnie ruchome dla swoich danych i nadać im sens.
Spróbuj napisać kod pythona kumulatywnej i wykładniczej średniej ruchomej bez użycia biblioteki pandas. To da ci znacznie bardziej dogłębną wiedzę o tym, jak są one obliczane i w jaki sposób różnią się od siebie.
Wciąż jest wiele do eksperymentowania. Spróbuj obliczyć częściową autokorelację między danymi wejściowymi a średnią ruchomą i spróbuj znaleźć jakąś zależność między nimi.
Jeśli chciałbyś dowiedzieć się więcej o DataFrames w pandas, weź udział w interaktywnym kursie DataCamp’s pandas Foundations.
.