Voortschrijdende gemiddelden in pandas

Inleiding
Een voortschrijdend gemiddelde, ook wel voortschrijdend of lopend gemiddelde genoemd, wordt gebruikt om de tijdreeksgegevens te analyseren door gemiddelden te berekenen van verschillende deelverzamelingen van de volledige gegevensreeks. Aangezien het gaat om het nemen van het gemiddelde van de dataset in de tijd, wordt het ook wel een voortschrijdend gemiddelde (MM) of voortschrijdend gemiddelde genoemd.
Er zijn verschillende manieren waarop het voortschrijdend gemiddelde kan worden berekend, maar één zo’n manier is om een vaste deelverzameling te nemen uit een complete reeks getallen. Het eerste voortschrijdend gemiddelde wordt berekend door het gemiddelde te nemen van de eerste vaste deelverzameling van getallen, en vervolgens wordt de deelverzameling gewijzigd door vooruit te gaan naar de volgende vaste deelverzameling (waarbij de toekomstige waarde in de deelverzameling wordt opgenomen, terwijl het vorige getal uit de reeks wordt uitgesloten).
Het voortschrijdend gemiddelde wordt meestal gebruikt bij tijdreeksgegevens om de kortetermijnfluctuaties vast te leggen, terwijl de aandacht wordt gericht op langere trends.
Een paar voorbeelden van tijdreeksgegevens zijn aandelenkoersen, weerberichten, luchtkwaliteit, bruto binnenlands product, werkgelegenheid, enz.
In het algemeen strijkt het voortschrijdend gemiddelde de gegevens glad.
Het voortschrijdend gemiddelde is de ruggengraat van veel algoritmen, en een van die algoritmen is het Autoregressief Geïntegreerd Voortschrijdend Gemiddelde Model (ARIMA), dat voortschrijdende gemiddelden gebruikt om voorspellingen te doen over tijdreeksgegevens.
Er zijn verschillende soorten voortschrijdende gemiddelden:
-
Simpel Voortschrijdend Gemiddelde (SMA): Simple Moving Average (SMA) maakt gebruik van een glijdend venster om het gemiddelde te nemen over een vastgesteld aantal tijdsperioden. Het is een gelijk gewogen gemiddelde van de voorgaande n gegevens.
Om SMA verder te begrijpen, nemen we een voorbeeld, een reeks van n waarden:

dan zal het gelijk gewogen voortschrijdend gemiddelde voor n datapunten in wezen het gemiddelde zijn van de vorige M datapunten, waarbij M de grootte is van het glijdend venster:

Ook voor de berekening van de opeenvolgende voortschrijdende gemiddelden wordt een nieuwe waarde aan de som toegevoegd en wordt de waarde van de vorige periode weggelaten, aangezien u het gemiddelde van de vorige perioden hebt en volledige optelling dus niet telkens vereist is:

- Cumulatief voortschrijdend gemiddelde (CMA): In tegenstelling tot het eenvoudig voortschrijdend gemiddelde, dat de oudste waarneming laat vallen wanneer de nieuwe wordt toegevoegd, houdt het cumulatief voortschrijdend gemiddelde rekening met alle vroegere waarnemingen. CMA is geen erg goede techniek om trends te analyseren en de gegevens af te vlakken. De reden hiervoor is dat het gemiddelde wordt genomen van alle eerdere gegevens tot aan het huidige gegevenspunt, dus een gelijk gewogen gemiddelde van de reeks van n waarden:



- Exponentieel bewegend gemiddelde (EMA): In tegenstelling tot SMA en CMA, geeft exponentieel voortschrijdend gemiddelde meer gewicht aan de recente prijzen en als gevolg daarvan kan het een beter model zijn of beter de beweging van de trend op een snellere manier vastleggen. De reactie van EMA is recht evenredig met het patroon van de gegevens.
Omdat EMA’s een groter gewicht toekennen aan recente gegevens dan aan oudere gegevens, reageren ze beter op de laatste prijsveranderingen dan SMA’s, waardoor de resultaten van EMA’s actueler zijn en EMA’s dus de voorkeur genieten boven andere technieken.
Genoeg theorie, niet? Laten we naar de praktische implementatie van het voortschrijdend gemiddelde springen.
Implementeren van voortschrijdend gemiddelde op tijdreeksgegevens
Simple Moving Average (SMA)
Laten we eerst dummy tijdreeksgegevens maken en proberen SMA te implementeren met alleen Python.
Veronderstel dat er een vraag naar een product is en dat deze gedurende 12 maanden (1 jaar) wordt waargenomen, en u moet voortschrijdende gemiddelden vinden voor vensterperioden van 3 en 4 maanden.
Import module
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| maand | vraag | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Laten we SMA berekenen voor een venstergrootte van 3, wat betekent dat u telkens drie waarden in aanmerking neemt om het voortschrijdend gemiddelde te berekenen, en dat voor elke nieuwe waarde, de oudste waarde wordt genegeerd.
Om dit te implementeren, zult u pandas iloc functie gebruiken, aangezien de demand kolom is wat u nodig hebt, zult u de positie van dat in de iloc functie vastzetten terwijl de rij een variabele i zal zijn die u zult blijven itereren tot u het einde van het dataframe bereikt.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| maand | vraag | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Laten we voor een sanity check ook de pandas ingebouwde rolling functie gebruiken en kijken of deze overeenkomt met ons aangepaste, op python gebaseerde, eenvoudig voortschrijdend gemiddelde.
df = df.iloc.rolling(window=3).mean()df.head()| maand | demand | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, dus zoals u kunt zien, komen de aangepaste en pandas voortschrijdende gemiddelden precies overeen, wat betekent dat uw implementatie van SMA correct was.
Laten we ook snel het eenvoudig voortschrijdend gemiddelde berekenen voor een window_size van 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| maand | vraag | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| maand | vraag | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.3333 | 289.5 | 289.5 |
Nu ga je de gegevens plotten van de voortschrijdende gemiddelden die je hebt berekend.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>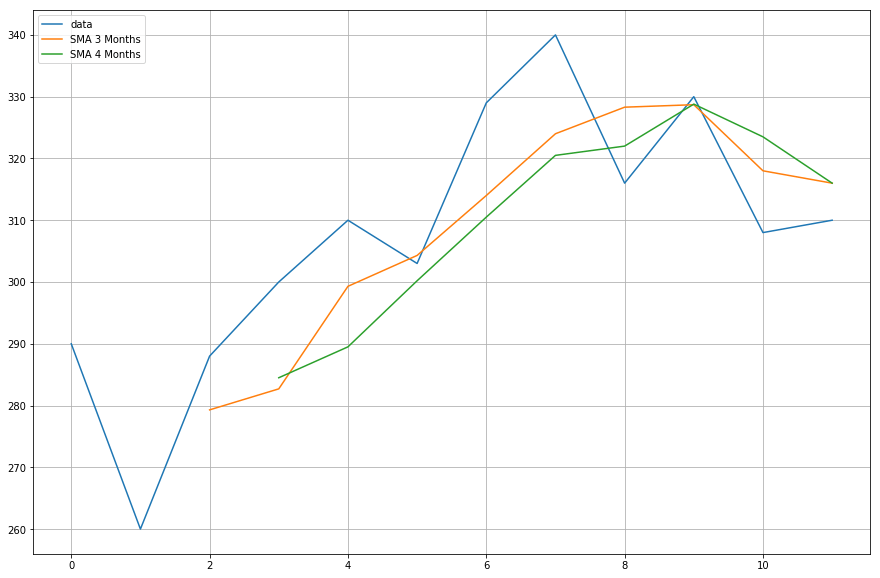
Cumulatief voortschrijdend gemiddelde
Ik denk dat we nu klaar zijn om over te gaan naar een echte dataset.
Voor het cumulatief voortschrijdend gemiddelde gebruiken we een air quality dataset die u kunt downloaden van deze link.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Datum | Tijd | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Het voorbewerken van gegevens is een essentiële stap wanneer u met gegevens werkt. Voor numerieke gegevens is een van de meest voorkomende voorbewerkingsstappen het controleren op NaN (Null)-waarden. Als er NaN-waarden zijn, kunt u ze vervangen door 0 of gemiddelde of voorgaande of volgende waarden, of ze zelfs weglaten. Hoewel vervangen normaliter een betere keuze is dan ze te laten vallen, aangezien deze dataset weinig NULL-waarden heeft, zal het laten vallen ervan de continuïteit van de reeks niet beïnvloeden.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64U kunt uit de bovenstaande uitvoer opmaken dat er ongeveer 114 NaN-waarden in alle kolommen zijn, maar u zult zien dat ze allemaal aan het einde van de tijdreeks staan, dus laten we ze snel laten vallen.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64U gaat een cumulatief voortschrijdend gemiddelde toepassen op de Temperature column (T), dus laten we die kolom snel scheiden van de volledige gegevens.
df_T = pd.DataFrame(df.iloc)df_T.head()
Nu, zul je de pandas expanding methode gebruiken om het cumulatieve gemiddelde van de bovenstaande gegevens te vinden. Als u zich herinnert uit de inleiding, neemt het cumulatief voortschrijdend gemiddelde, in tegenstelling tot het eenvoudig voortschrijdend gemiddelde, alle voorgaande waarden in aanmerking bij de berekening van het gemiddelde.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Gegevens uit tijdreeksen worden uitgezet ten opzichte van de tijd, dus laten we de datum- en tijdkolom combineren en omzetten in een datetime object. Om dit te bereiken gebruikt u de datetime module van python (Bron: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Laten we de index van het temperature dataframe veranderen in datetime.
df_T.index = df.DateTimeLaten we nu de actuele temperatuur en het cumulatief voortschrijdend gemiddelde plotten ten opzichte van de tijd.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponentieel voortschrijdend gemiddelde
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DatumTijd | |||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>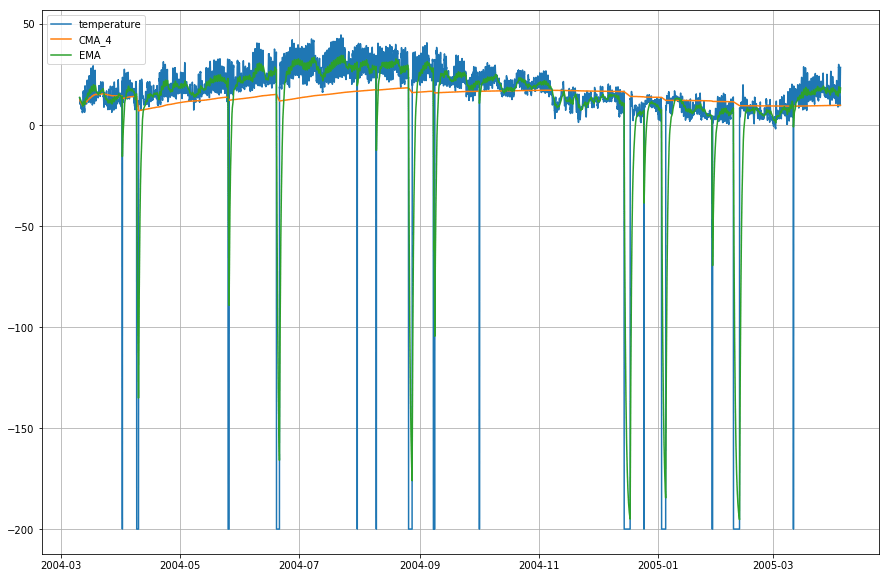
Wow! Uit bovenstaande grafiek kunt u opmaken dat de Exponential Moving Average (EMA) het patroon van de gegevens uitstekend vastlegt, terwijl de Cumulative Moving Average (CMA) daar ver bij achterblijft.
Ga verder!
Gefeliciteerd met het afronden van de tutorial.
Deze tutorial was een goed startpunt over hoe je de voortschrijdende gemiddelden van je gegevens kunt berekenen en er iets zinnigs mee kunt doen.
Probeer de cumulatieve en exponentieel voortschrijdend gemiddelde python code te schrijven zonder gebruik te maken van de pandas library. Dat zal je veel meer diepgaande kennis geven over hoe ze berekend worden en op welke manieren ze van elkaar verschillen.
Er valt nog veel te experimenteren. Probeer de gedeeltelijke autocorrelatie tussen de invoergegevens en het voortschrijdend gemiddelde te berekenen, en probeer een verband tussen die twee te vinden.
Als je meer wilt leren over DataFrames in pandas, volg dan de interactieve cursus pandas Foundations van DataCamp.