De-Multiplexer is een combinatorische schakeling die de omgekeerde werking van Multiplexer uitvoert. Zij heeft één ingang, ‘n’ selectielijnen en maximaal 2n uitgangen. De ingang wordt verbonden met een van deze uitgangen op basis van de waarden van de selectielijnen.

Omdat er ‘n’ selectielijnen zijn, zullen er 2n mogelijke combinaties van nullen en enen zijn. Elke combinatie kan dus slechts één uitgang selecteren. De-Multiplexer wordt ook wel De-Mux genoemd.

1×4 De-Multiplexer

1×4 De-Multiplexer heeft een ingang I, twee selectielijnen, s1 & s0 en vier uitgangen Y3, Y2, Y1 &Y0. Het blokschema van 1×4 De-Multiplexer is weergegeven in de volgende figuur.

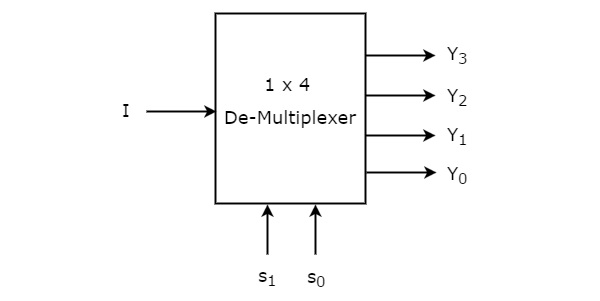
De enkele ingang “I” wordt verbonden met een van de vier uitgangen, Y3 tot Y0 op basis van de waarden van de selectielijnen s1 & s0. De waarheidstabel van de 1×4 De-Multiplexer is hieronder weergegeven.

Selectie-ingangen		Uitgangen
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	I
0	1	0	0	I	0
1	0	0	I	0	0
1	I	0	0	0

Vanuit de bovenstaande waarheidstabel, kunnen we de Booleaanse functies voor elke uitgang direct schrijven als

$Y_{3}=s_{1}s_{0}I$$

$$Y_{2}=s_{1}{s_{0}}’I$$

$Y_{1}={s_{1}}’s_{0}I$

$Y_{0}={s_1}'{s_{0}}’I$

We kunnen deze Booleaanse functies implementeren met behulp van Inverters & 3-input AND poorten. Het schakelschema van 1×4 De-Multiplexer is weergegeven in de volgende figuur.

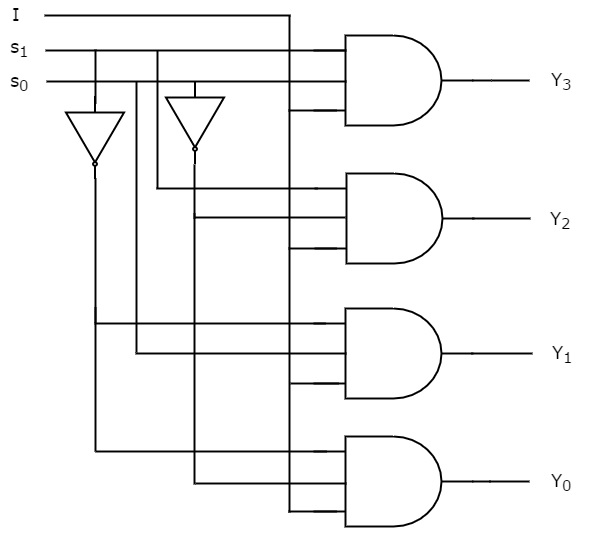
We kunnen de werking van het bovenstaande circuit gemakkelijk begrijpen. Op dezelfde manier kunt u een 1×8 De-Multiplexer en een 1×16 De-Multiplexer implementeren door dezelfde procedure te volgen.

Implementatie van hogere-orde De-Multiplexers

Nu gaan we de volgende twee hogere-orde De-Multiplexers implementeren met behulp van lagere-orde De-Multiplexers.

• 1×8 De-Multiplexer
• 1×16 De-Multiplexer

1×8 De-Multiplexer

In deze sectie, laat ons 1×8 De-Multiplexer implementeren met behulp van 1×4 De-Multiplexers en 1×2 De-Multiplexer. We weten dat de 1×4 De-Multiplexer één ingang, twee selectielijnen en vier uitgangen heeft. Terwijl de 1×8 De-Multiplexer één ingang, drie selectielijnen en acht uitgangen heeft.

We hebben dus twee 1×4 De-Multiplexers nodig in de tweede trap om de uiteindelijke acht uitgangen te krijgen. Aangezien het aantal ingangen in de tweede trap twee is, hebben we in de eerste trap een 1×2 De-Multiplexer nodig, zodat de uitgangen van de eerste trap de ingangen van de tweede trap worden. De ingang van deze 1×2 De-Multiplexer zal de totale ingang zijn van de 1×8 De-Multiplexer.

Laat de 1×8 De-Multiplexer één ingang I hebben, drie selectielijnen s2, s1 & s0 en de uitgangen Y7 tot Y0. De waarheidstabel van de 1×8 De-Multiplexer is hieronder weergegeven.

Selectie ingangen			Uitgangen
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

We kunnen 1×8 De-Multiplexer met behulp van lagere orde Multiplexers eenvoudig implementeren door de bovenstaande waarheidstabel te beschouwen. Het blokschema van 1×8 De-Multiplexer is weergegeven in de volgende figuur.

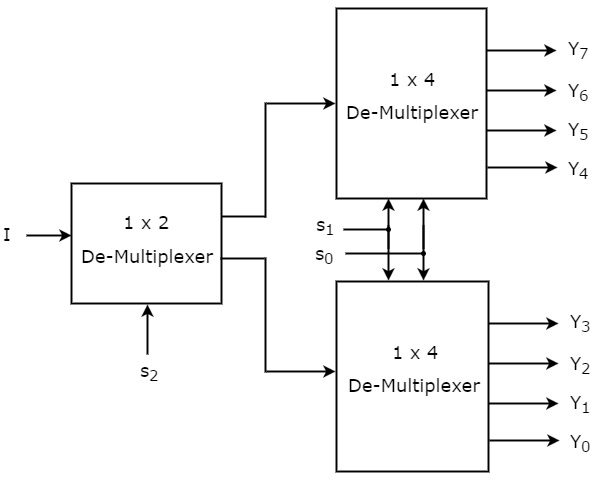
De gemeenschappelijke selectielijnen, s1 & s0 worden toegepast op beide 1×4 De-Multiplexers. De uitgangen van de bovenste 1×4 De-Multiplexer zijn Y7 tot Y4 en de uitgangen van de onderste 1×4 De-Multiplexer zijn Y3 tot Y0.

De andere selectielijn, s2 wordt toegepast op de 1×2 De-Multiplexer. Als s2 nul is, dan zal een van de vier uitgangen van de onderste 1×4 De-Multiplexer gelijk zijn aan ingang, I gebaseerd op de waarden van selectielijnen s1 & s0. Evenzo, als s2 één is, dan zal één van de vier uitgangen van de bovenste 1×4 De-Multiplexer gelijk zijn aan ingang, I op basis van de waarden van selectielijnen s1 & s0.

1×16 De-Multiplexer

In deze sectie, laten we 1×16 De-Multiplexer implementeren met behulp van 1×8 De-Multiplexers en 1×2 De-Multiplexer. We weten dat de 1×8 De-Multiplexer één ingang, drie selectielijnen en acht uitgangen heeft. Terwijl de 1×16 De-Multiplexer één ingang, vier selectielijnen en zestien uitgangen heeft.

We hebben dus twee 1×8 De-Multiplexers nodig in de tweede trap om de uiteindelijke zestien uitgangen te krijgen. Omdat het aantal ingangen in de tweede trap twee is, hebben we in de eerste trap een 1×2 De-Multiplexer nodig, zodat de uitgangen van de eerste trap de ingangen van de tweede trap worden. De ingang van deze 1×2 De-Multiplexer zal de totale ingang zijn van de 1×16 De-Multiplexer.

Stel dat de 1×16 De-Multiplexer één ingang I heeft, vier selectielijnen s3, s2, s1 & s0 en de uitgangen Y15 tot Y0. Het blokschema van 1×16 De-Multiplexer met behulp van Multiplexers van lagere orde is weergegeven in de volgende figuur.

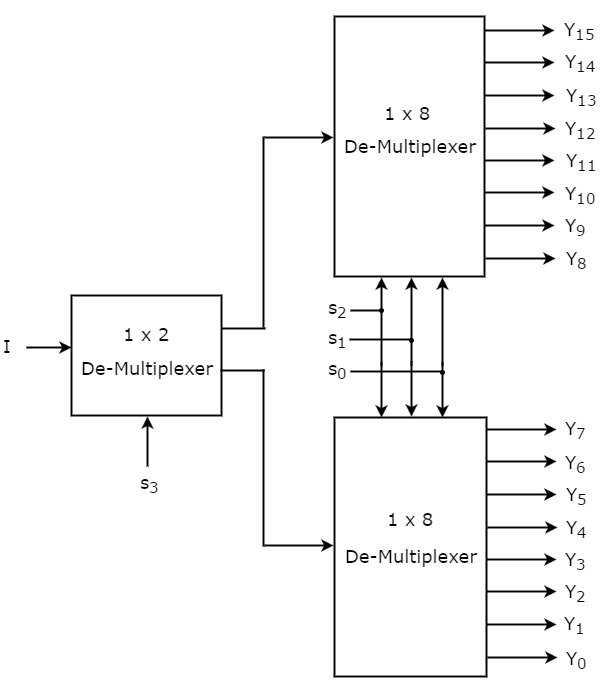
De gemeenschappelijke selectielijnen s2, s1 & s0 worden toegepast op beide 1×8 De-Multiplexers. De uitgangen van de bovenste 1×8 De-Multiplexer zijn Y15 tot Y8 en de uitgangen van de onderste 1×8 De-Multiplexer zijn Y7 tot Y0.

De andere selectielijn, s3, wordt toegepast op de 1×2 De-Multiplexer. Als s3 nul is, dan zal een van de acht uitgangen van de 1×8 De-Multiplexer gelijk zijn aan ingang I, gebaseerd op de waarden van de selectielijnen s2, s1 & s0. Evenzo, als s3 één is, dan zal één van de 8 uitgangen van de bovenste 1×8 De-Multiplexer gelijk zijn aan ingang, I gebaseerd op de waarden van selectielijnen s2, s1 & s0.