Een paar weken geleden heb ik onze afdrukbare alfabetpuzzels gedeeld en die waren een groot succes bij ons thuis. Dus, nadat ik een paar verzoeken had gekregen voor getallenpuzzels, heb ik een aantal afdrukbare getallenpuzzels gemaakt voor de getallen 1-10.

Tallen kunnen op verschillende manieren worden weergegeven, zoals foto’s, getallenwoorden, basistienblokken of telmerken {om er maar een paar te noemen}. En aangezien dit een belangrijke vaardigheid is voor jonge kinderen om te leren, dacht ik dat getallenpuzzels een leuke manier zouden zijn om dit leerdoel te bereiken.

Note: Gratis download te vinden aan het EINDE van dit bericht.

*Dit bericht bevat links naar andere sites.

Afdrukbare getallenpuzzels {voor de getallen 1-10}

Om de getallenpuzzels te maken, hoef je alleen maar de puzzels die je wilt hebben op karton af te drukken {gewoon papier is misschien te dun} en de puzzelstukjes uit te knippen. Je kunt ze ook lamineren, maar zorg ervoor dat je het laminaat een beetje bijsnijdt, anders passen de puzzelstukjes niet goed.

Op elk stukje van de getallenpuzzel staat een manier waarop het getal kan worden weergegeven, perfect voor peuters of kleuters. U vindt

• dobbelsteenpunt patronen,
• basis tien blokken,
• telmerken,
• tien frames,
• getal woorden,
• tel vingers,
• en een beetje optellen, ook.

U kunt uw kind/leerling uitdagen de puzzel zonder hulp te proberen,

maar er zijn getallenmatten die als basis of sjabloon kunnen dienen die de activiteit wat gemakkelijker maken.

De puzzel is zelfcontrolerend als hij af is, omdat hij het juiste getal vormt, maar u kunt de getallen ook op de achterkant schrijven, als u dat wilt.

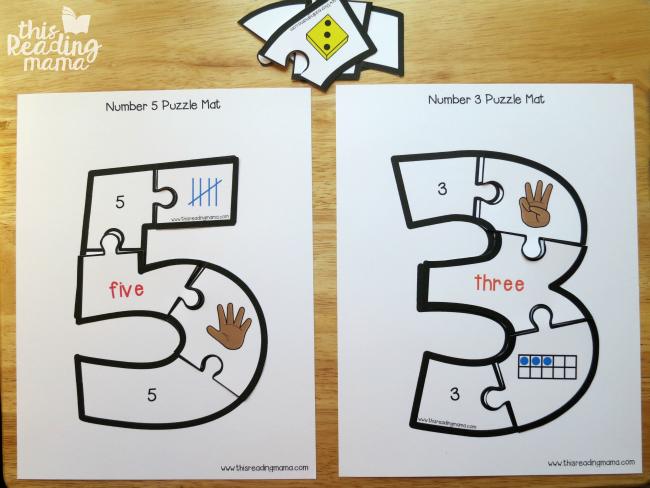
Een ander leuk idee voor een kind dat toe is aan een grotere uitdaging is om twee getalpuzzels te nemen en de stukjes door elkaar te halen. Het kind/ de leerling moet de stukjes sorteren om uit te zoeken bij welke cijferpuzzel de stukjes horen. Probeer het met de getallenmatten {zoals hierboven afgebeeld} of zonder ze voor een extra uitdaging.

Natuurlijk wil je dat het kind bij elke bewerkte puzzel in staat is om elk van de visuele voorstellingen van het getal te herkennen. Dit gebeurt tijdens het maken van de puzzel, maar kan ook achteraf nog eens worden gedaan.