pandasの移動平均

はじめに
移動平均は、転がし平均または走行平均とも呼ばれ、完全なデータセットの異なるサブセットの平均を計算して、時系列データを分析するために使用されるものです。 時間の経過とともにデータセットの平均を取ることを含むので、移動平均(MM)またはローリング平均とも呼ばれます。
ローリング平均を計算できる方法はさまざまですが、その1つは完全な一連の数値から一定の部分集合を取ることです。 最初の移動平均は、最初の固定された部分集合の数値を平均することによって計算され、その後、次の固定された部分集合に進むことによって部分集合が変更されます(前の数値を系列から除外しながら、将来の数値を部分集合に含める)
移動平均は主に時系列データで使われ、長い傾向に注目しながら短期の変動をとらえられます。
時系列データの例としては、株価、天気予報、大気質、国内総生産、雇用などがあります。
一般に、移動平均はデータを平滑化させます。
移動平均は多くのアルゴリズムのバックボーンであり、そのようなアルゴリズムの 1 つが自己回帰統合移動平均モデル (ARIMA) で、移動平均を使用して時系列データの予測を行います。
移動平均にはさまざまなタイプがあります:
-
単純移動平均 (SMA): 単純移動平均(SMA)は、スライディングウィンドウを使用して、設定された期間の平均を取ります。 これは、前のn個のデータの均等な重み付けされた平均です。
SMA をさらに理解するために、n 個の値のシーケンスを例に挙げます。

すると、n 個のデータ ポイントの等加重移動平均は、基本的に以前の M 個のデータ ポイント(M はスライド ウィンドウのサイズ)の平均となります。

同様に、連続する移動平均値を計算する場合、新しい値が合計に追加され、前の期間の値は削除されます。 新しいものが追加されると最も古い観測値を削除する単純移動平均とは異なり、累積移動平均は、すべての以前の観測値を考慮します。 CMAは、トレンドを分析し、データを平滑化するための非常に良い手法ではありません。 なぜなら、現在のデータポイントまでの過去のデータをすべて平均化するので、一連のn個の値の等加重平均になるからです。



- 指数移動平均 (EMA)です。 SMAやCMAとは異なり、指数移動平均は直近の価格に重きを置き、その結果、より良いモデルとして、あるいはより速くトレンドの動きを捉えることができるのです。 EMAの反応は、データのパターンに正比例します。
EMAは古いデータよりも最近のデータに高い重みを与えるので、SMAと比較して最新の価格変動に反応しやすく、EMAからの結果はよりタイムリーになり、したがってEMAは他の手法よりも好まれます。
理論は十分ですよね?
Implementing Moving Average on Time Series Data
Simple Moving Average (SMA)
まず、ダミー時系列データを作成して、PythonだけでSMAを実装してみましょう。
ある製品の需要があり、12ヶ月(1年)観測されていると仮定し、ウィンドウ期間3ヶ月と4ヶ月間の移動平均を見つける必要があるとしましょう。
インポートモジュール
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| month | 需要 | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | |
| 260 | ||
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
ウィンドウサイズ3でのSMAを計算してみます。 つまり、移動平均を計算するために毎回3つの値を考慮し、新しい値ごとに、最も古い値は無視されることになります。
これを実装するには、pandasのiloc関数を使います。demand列が必要なので、iloc関数でその位置を固定し、行は変数iにして、データフレームの最後に達するまで繰り返し実行します。
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| month | demand | SMA_3 | |||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | ||||
| 1 | 2 | 260 | NaN | ||||
| 2 | 3 | 288 | 279.1 | NaN> | Nb> | Nb> | 260 |
| 3 | 4 | 300 | 282.7 | ||||
| 4 | 5 | 310 | 299.3 |
健全性をチェックするために、pandas 内蔵の rolling 関数も使用して、私たちのカスタム Python ベース単純移動平均と一致するかどうかを確認しましょう。
df = df.iloc.rolling(window=3).mean()df.head()| 月 | 需要 | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | |
| 1 | 2 | 260 | NaN | |
| 2 | 3 | 288 | 279。3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, so you can see, the custom and pandas moving averages match exactly, which means your implementation of SMA was correct.
Simple moving average for a window_size of 4も早速計算してみましょう。
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| 月 | 需要 | SMA_3 | pandas_SMA_3 | SMA_4 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | ||||||
| 1 | 2 | 260NaN | ||||||||
| 2 | 3 | 288 | 279.K | NaN | NaN | NaN | NaN | NaN4253 | 279.3333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.7 | 282.666667 | 284.5 | ||||
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| month | demand | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 | 290 | NaN | NaN | ||||||||||
| 1 | 2 | NaN425 | 260 | NaN | NaN | ||||||||
| 2 | 3 | 288 | 279.1 | NaN | NaN | Nb> | NaN | NaN | Nb>NaN | Nb>NaN4253 | 279.333333 | NaN | |
| 3 | 4 | 300 | 282.7 | 282.3 | 28325> | NaN | NaN | NaN> | 282.4 | 282.6 | 284.5 | 284.5 | |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
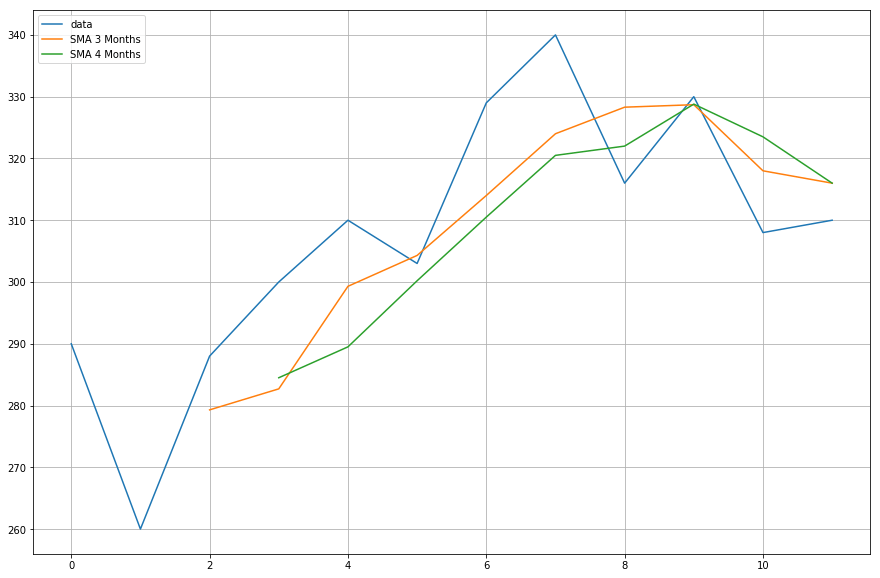
では、計算した移動平均のデータをプロットしてみましょう。
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>
Cumulative Moving Average
これで実際のデータセットに移行できると思います。
累積移動平均は、このリンクからダウンロードできるair quality datasetを使ってみましょう。
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S3(NMHC) | NOx(PT) | T08.S4(NO2) | PT08.S3(NO2)S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 | |||
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 | |||
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 | |||
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 | |||
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
前処理はデータを扱うときに必ず行うべきステップである。 数値データの場合、最も一般的な前処理の1つはNaN (Null)値があるかどうかをチェックすることです。 もしNaN値があれば、それを0や平均値、前後の値で置き換えたり、削除したりすることができます。 通常は置換する方が削除するより良い選択ですが、このデータセットにはNULL値がほとんどないので、削除しても系列の連続性には影響しません。
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64上の出力から、すべての列で約114個のNaN値があることがわかりますが、それらはすべて時系列の最後にあることがわかりますので、すばやく削除してみましょう。
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64 Temperature column (T)には累積移動平均をかけるので、この列を全データから分離してみましょう。
df_T = pd.DataFrame(df.iloc)df_T.head()さて、次は。 は、pandas expanding メソッドを使って、上記のデータの累積平均を求めます。
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |||||
|---|---|---|---|---|---|---|
| 0 | 13.XXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX6 | NaN | ||||
| 1 | 13.3 | NaN | ||||
| 2 | 11.1 | 13.3 | 13.4 | |||
| 180089 | NaN | |||||
| 3 | 11.0 | 12.450000 | ||||
| 4 | 11.3 | 11.0 | 11.4 | 12.0 | 12.0 | 12.200000 |
| 5 | 11.2 | 12.033333 | ||||
| 6 | 11.3 | 11.928571 | ||||
| 7 | 10.7 | 11.775000 | ||||
| 8 | 10.7 | 11.655556 | ||||
| 9 | 10.3 | 11.520000 |
時系列データは時間を基準にプロットするので、日付と時間の列をまとめて、datetimeオブジェクトに変換してみましょう。 これを実現するために、pythonのdatetimeモジュールを使います(出典:Time Series Tutorial)。
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))temperatureデータフレームのインデックスをdatetimeに変更しましょう。
df_T.index = df.DateTime次に、実際の温度と累積移動平均を時間に対してプロットしてみましょう。
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>

指数移動平均
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | ||||||
|---|---|---|---|---|---|---|---|---|
| DateTime | ||||||||
| 2004-> | 200403-10 18:00:00 | 13.6 | NaN | 13.600000 | ||||
| 2004-03-10 19:00:00 | 13.600000 | 13.3 | NaN | 13.585366 | ||||
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.0 | 13.585366 | NaN | 13.0 | 13.0 | NaN |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 | |||||
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>
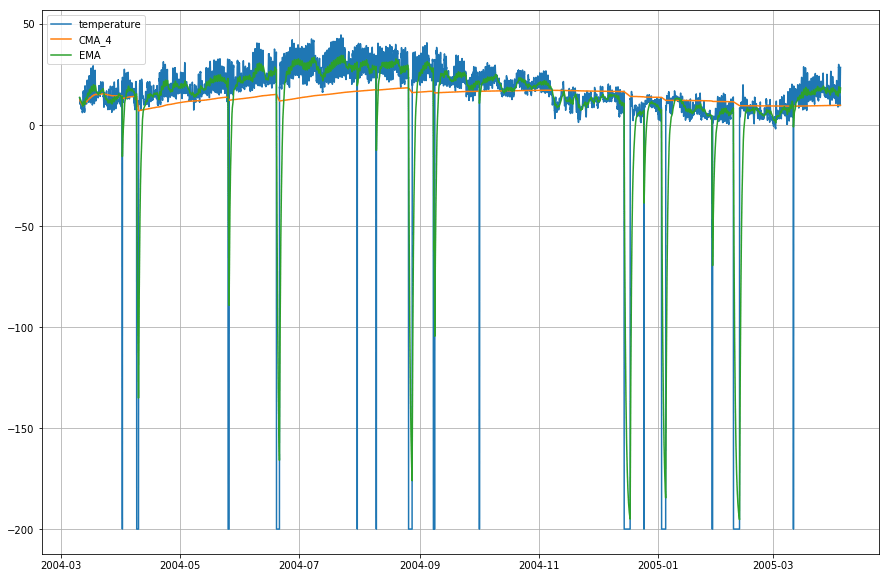
Wow! 上のグラフからわかるように、Exponential Moving Average (EMA) はデータのパターンを捉えるのに素晴らしい仕事をしているのに対し、Cumulative Moving Average (CMA) はかなりの差で欠けています。
Go Further!
このチュートリアルは、データの移動平均を計算し、それを理解する方法についての良い出発点でした。
pandasライブラリを使用せずに累積および指数移動平均のpythonコードを書いてみてください。 そうすれば、それらがどのように計算され、どのような点で互いに異なっているのかについて、より深い知識を得ることができます。 入力データと移動平均の部分自己相関を計算してみて、両者の間に何らかの関係があるかどうか試してみてください。
pandas の DataFrames についてもっと学びたい場合は、DataCamp の pandas Foundations インタラクティブコースに参加してみてください。