Questo articolo è stato originariamente pubblicato sul sito di Cadence. Viene qui ristampato con il permesso di Cadence.

Le reti neurali convoluzionali (CNN) sono ampiamente utilizzate nei problemi di riconoscimento di modelli e immagini in quanto hanno una serie di vantaggi rispetto ad altre tecniche. Questo white paper copre le basi delle CNN, compresa una descrizione dei vari strati utilizzati. Usando il riconoscimento della segnaletica stradale come esempio, discutiamo le sfide del problema generale ed introduciamo gli algoritmi ed il software di implementazione sviluppati da Cadence che possono barattare il carico computazionale e l’energia per una degradazione modesta nei tassi di riconoscimento del segno. Delineiamo le sfide dell’uso delle CNN nei sistemi embedded e introduciamo le caratteristiche chiave del processore di segnale digitale (DSP) Cadence® Tensilica® Vision P5 per Imaging e Computer Vision e del software che lo rendono così adatto alle applicazioni CNN in molti compiti di imaging e riconoscimento correlati.

Cos’è una CNN?

Una rete neurale è un sistema di “neuroni” artificiali interconnessi che scambiano messaggi tra loro. Le connessioni hanno pesi numerici che sono sintonizzati durante il processo di formazione, in modo che una rete correttamente addestrata risponda correttamente quando le viene presentata un’immagine o un modello da riconoscere. La rete consiste di strati multipli di “neuroni” che rilevano le caratteristiche. Ogni strato ha molti neuroni che rispondono a diverse combinazioni di input dagli strati precedenti. Come mostrato nella Figura 1, gli strati sono costruiti in modo che il primo strato rilevi un insieme di modelli primitivi nell’input, il secondo strato rileva modelli di modelli, il terzo strato rileva modelli di quei modelli, e così via. Le CNN tipiche usano da 5 a 25 strati distinti di riconoscimento dei modelli.

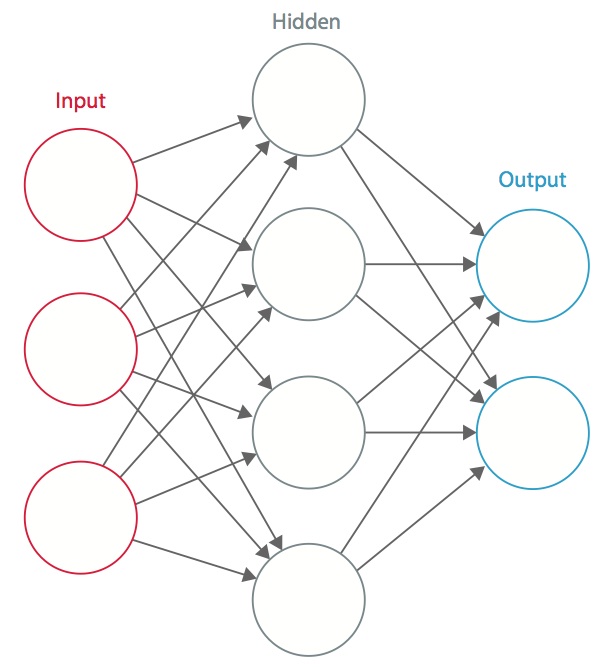
Figura 1: Una rete neurale artificiale

L’addestramento viene eseguito usando un set di dati “etichettati” di input in un vasto assortimento di modelli di input rappresentativi che sono etichettati con la loro risposta di output prevista. L’addestramento utilizza metodi generici per determinare iterativamente i pesi per i neuroni intermedi e finali delle caratteristiche. La figura 2 dimostra il processo di addestramento a livello di blocco.

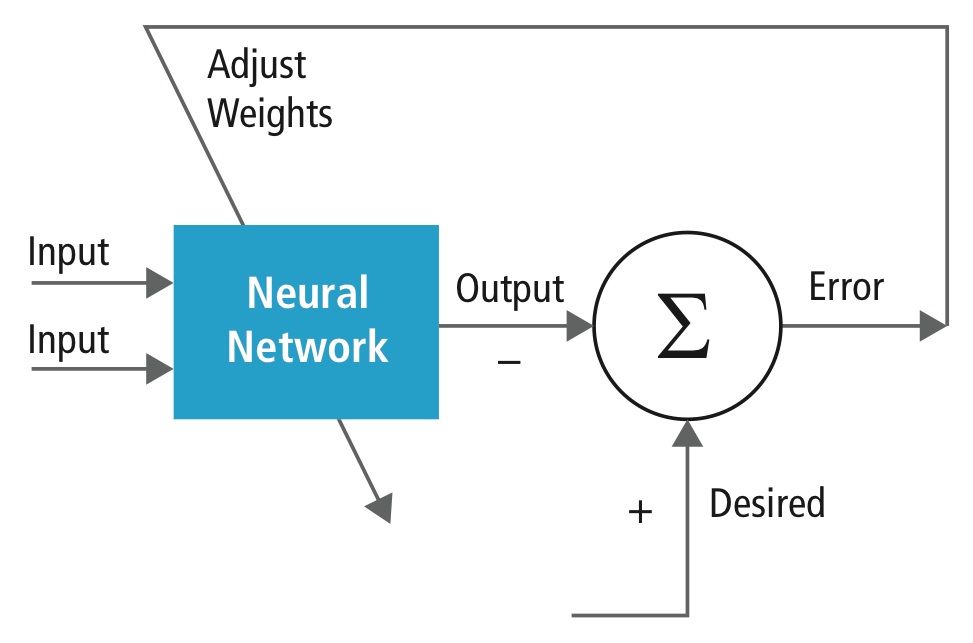
Figura 2: Addestramento delle reti neurali

Le reti neurali sono ispirate ai sistemi neurali biologici. L’unità computazionale di base del cervello è un neurone e sono collegati con sinapsi. La figura 3 confronta un neurone biologico con un modello matematico di base.

Figura 3: Illustrazione di un neurone biologico (in alto) e il suo modello matematico (in basso)

In un sistema neurale animale reale, un neurone riceve segnali in ingresso dai suoi dendriti e produce segnali in uscita lungo il suo assone. L’assone si ramifica e si collega tramite sinapsi ai dendriti di altri neuroni. Quando la combinazione dei segnali di ingresso raggiunge una condizione di soglia tra i suoi dendriti di ingresso, il neurone viene attivato e la sua attivazione viene comunicata ai neuroni successivi.

Nel modello computazionale della rete neurale, i segnali che viaggiano lungo gli assoni (ad esempio, x0) interagiscono in modo moltiplicativo (ad esempio, w0x0) con i dendriti dell’altro neurone in base alla forza sinaptica a quella sinapsi (ad esempio, w0). I pesi sinaptici sono apprendibili e controllano l’influenza di un neurone o di un altro. I dendriti portano il segnale al corpo cellulare, dove sono tutti sommati. Se la somma finale è superiore a una soglia specificata, il neurone scatta, inviando uno spike lungo il suo assone. Nel modello computazionale, si assume che i tempi precisi degli spari non abbiano importanza e che solo la frequenza degli spari comunichi informazioni. Sulla base dell’interpretazione del rate code, il tasso di accensione del neurone è modellato con una funzione di attivazione ƒ che rappresenta la frequenza degli spike lungo l’assone. Una scelta comune di funzione di attivazione è sigmoide. In sintesi, ogni neurone calcola il prodotto di punti degli ingressi e dei pesi, aggiunge il bias, e applica la non linearità come funzione di attivazione (per esempio, seguendo una funzione di risposta sigmoidea).

Una CNN è un caso speciale della rete neurale descritta sopra. Una CNN consiste in uno o più strati convoluzionali, spesso con uno strato di sottocampionamento, che sono seguiti da uno o più strati completamente connessi come in una rete neurale standard.

La progettazione di una CNN è motivata dalla scoperta di un meccanismo visivo, la corteccia visiva, nel cervello. La corteccia visiva contiene molte cellule che sono responsabili della rilevazione della luce in piccole sottoregioni sovrapposte del campo visivo, chiamate campi recettivi. Queste cellule agiscono come filtri locali sullo spazio di input, e le cellule più complesse hanno campi recettivi più grandi. Lo strato di convoluzione in una CNN svolge la funzione che viene eseguita dalle cellule della corteccia visiva.

Una tipica CNN per il riconoscimento dei segnali stradali è mostrata nella Figura 4. Ogni caratteristica di uno strato riceve input da un insieme di caratteristiche situate in un piccolo quartiere nello strato precedente chiamato campo recettivo locale. Con i campi recettivi locali, le caratteristiche possono estrarre caratteristiche visive elementari, come bordi orientati, punti finali, angoli, ecc. che vengono poi combinati dagli strati superiori.

Nel modello tradizionale di riconoscimento di pattern/immagini, un estrattore di caratteristiche progettato a mano raccoglie informazioni rilevanti dall’input ed elimina le variabili irrilevanti. L’estrattore è seguito da un classificatore addestrabile, una rete neurale standard che classifica i vettori di caratteristiche in classi.

In una CNN, gli strati di convoluzione svolgono il ruolo di estrattore di caratteristiche. Ma non sono progettati a mano. I pesi del kernel del filtro di convoluzione sono decisi come parte del processo di formazione. Gli strati di convoluzione sono in grado di estrarre le caratteristiche locali perché limitano i campi recettivi degli strati nascosti ad essere locali.

Figura 4: Schema a blocchi tipico di una CNN

Le CNN sono usate in diverse aree, incluso il riconoscimento di immagini e modelli, il riconoscimento del parlato, l’elaborazione del linguaggio naturale e l’analisi video. Ci sono diverse ragioni per cui le reti neurali convoluzionali stanno diventando importanti. Nei modelli tradizionali per il riconoscimento dei modelli, gli estrattori di caratteristiche sono progettati a mano. Nelle CNN, i pesi dello strato convoluzionale usato per l’estrazione delle caratteristiche e lo strato completamente connesso usato per la classificazione sono determinati durante il processo di formazione. Le strutture di rete migliorate delle CNN portano a un risparmio nei requisiti di memoria e di complessità di calcolo e, allo stesso tempo, danno migliori prestazioni per applicazioni in cui l’input ha una correlazione locale (per esempio, immagine e discorso).

Grandi requisiti di risorse computazionali per l’addestramento e la valutazione delle CNN sono talvolta soddisfatti da unità di elaborazione grafica (GPU), DSP, o altre architetture di silicio ottimizzate per un alto rendimento e bassa energia quando si eseguono i modelli idiosincratici del calcolo delle CNN. Infatti, processori avanzati come il Tensilica Vision P5 DSP for Imaging and Computer Vision di Cadence hanno un insieme quasi ideale di risorse di calcolo e di memoria necessarie per eseguire le CNN ad alta efficienza.

Nelle applicazioni di riconoscimento di modelli e immagini, i migliori tassi di rilevamento corretto (CDR) possibili sono stati ottenuti usando le CNN. Per esempio, le CNN hanno raggiunto un CDR del 99,77% usando il database MNIST di cifre scritte a mano, un CDR del 97,47% con il dataset NORB di oggetti 3D e un CDR del 97,6% su ~5600 immagini di più di 10 oggetti. Le CNN non solo danno le migliori prestazioni rispetto ad altri algoritmi di rilevamento, ma superano anche gli esseri umani in casi come la classificazione di oggetti in categorie a grana fine come la particolare razza di cane o la specie di uccello .

La figura 5 mostra una tipica pipeline di algoritmi di visione, che consiste di quattro fasi: pre-elaborazione dell’immagine, rilevamento delle regioni di interesse (ROI) che contengono oggetti probabili, riconoscimento degli oggetti e processo decisionale della visione. La fase di pre-elaborazione di solito dipende dai dettagli dell’input, specialmente dal sistema di telecamere, ed è spesso implementata in un’unità cablata al di fuori del sottosistema di visione. Il processo decisionale alla fine della pipeline opera tipicamente sugli oggetti riconosciuti – può prendere decisioni complesse, ma opera su molti meno dati, quindi queste decisioni non sono di solito problemi computazionalmente difficili o che richiedono molta memoria. La grande sfida è nelle fasi di rilevamento e riconoscimento degli oggetti, dove le CNN stanno avendo un ampio impatto.

Figura 5: Pipeline degli algoritmi di visione

Strati di CNN

Posizionando più e diversi strati in una CNN, vengono costruite architetture complesse per problemi di classificazione. Quattro tipi di strati sono i più comuni: strati di convoluzione, strati di pooling/sottocampionamento, strati non lineari e strati completamente connessi.

Strati di convoluzione

L’operazione di convoluzione estrae diverse caratteristiche dell’input. Il primo strato di convoluzione estrae caratteristiche di basso livello come bordi, linee e angoli. Gli strati di livello superiore estraggono caratteristiche di livello superiore. La figura 6 illustra il processo di convoluzione 3D usato nelle CNN. L’input è di dimensioni N x N x D e viene convoluto con H kernel, ognuno di
dimensioni k x k x D separatamente. La convoluzione di un input con un kernel produce una caratteristica di output, e con H kernel indipendentemente produce H caratteristiche. Partendo dall’angolo in alto a sinistra dell’input, ogni kernel viene spostato da sinistra a destra, un elemento alla volta. Una volta raggiunto l’angolo in alto a destra, il kernel viene spostato di un elemento verso il basso, e di nuovo il kernel viene spostato da sinistra a destra, un elemento alla volta. Questo processo viene ripetuto fino a quando
il kernel raggiunge l’angolo in basso a destra. Per il caso in cui N = 32 e k = 5, ci sono 28 posizioni uniche da sinistra a destra e 28 posizioni uniche dall’alto in basso che il kernel può prendere. Corrispondendo a queste posizioni, ogni caratteristica nell’output conterrà 28×28 (cioè, (N-k+1) x (N-k+1)) elementi. Per ogni posizione del kernel in un processo a finestra scorrevole, k x k x D elementi di input e k x k x D elementi del kernel sono moltiplicati elemento per elemento e accumulati. Così, per creare un elemento di una caratteristica di uscita, sono richieste k x k x D operazioni di moltiplicazione-accumulazione.

Figura 6: Rappresentazione pittorica del processo di convoluzione

Strati di pooling/sottocampionamento

Lo strato di pooling/sottocampionamento riduce la risoluzione delle caratteristiche. Rende le caratteristiche robuste contro il rumore e la distorsione. Ci sono due modi per fare il pooling: max pooling e average pooling. In entrambi i casi, l’input è diviso in spazi bidimensionali non sovrapposti. Per esempio, nella figura 4, lo strato 2 è lo strato di pooling. Ogni caratteristica di input è 28×28 ed è divisa in 14×14 regioni di dimensioni 2×2. Per il pooling medio, viene calcolata la media dei quattro valori nella regione. Per il max pooling, viene selezionato il valore massimo dei quattro valori.

La figura 7 elabora ulteriormente il processo di pooling. L’input è di dimensioni 4×4. Per il sottocampionamento 2×2, un’immagine 4×4 è divisa in quattro matrici non sovrapposte di dimensioni 2×2. Nel caso di max pooling, il valore massimo dei quattro valori nella matrice 2×2 è l’output. Nel caso del pooling medio, la media dei quattro valori è l’uscita. Notate che per l’uscita con indice (2,2), il risultato della media è una frazione che è stata arrotondata al numero intero più vicino.

Figura 7: Rappresentazione pittorica di max pooling e average pooling

Strati non lineari

Le reti neurali in generale e le CNN in particolare si basano su una funzione di “trigger” non lineare per segnalare l’identificazione distinta di caratteristiche probabili su ogni strato nascosto. Le CNN possono usare una varietà di funzioni specifiche – come le unità lineari rettificate (ReLU) e le funzioni di trigger continue (non lineari) – per implementare in modo efficiente questo trigger non lineare.

ReLU

Una ReLU implementa la funzione y = max(x,0), quindi le dimensioni di input e output di questo strato sono uguali. Aumenta le proprietà non lineari della funzione di decisione e dell’intera rete senza influenzare i campi recettivi dello strato di convoluzione. In confronto alle altre funzioni non lineari usate nelle CNN (per esempio, tangente iperbolica, assoluta di tangente iperbolica, e sigmoide), il vantaggio di una ReLU è che la rete si allena molte volte più velocemente. La funzionalità ReLU è illustrata nella Figura 8, con la sua funzione di trasferimento tracciata sopra la freccia.

Figura 8: Rappresentazione pittorica della funzionalità ReLU

Funzione di attivazione continua (non lineare)

Lo strato non lineare opera elemento per elemento in ogni caratteristica. Una funzione di attivazione continua può essere tangente iperbolica (Figura 9), assoluta di tangente iperbolica (Figura 10), o sigmoide (Figura 11). La Figura 12 dimostra come la non linearità viene applicata elemento per elemento.

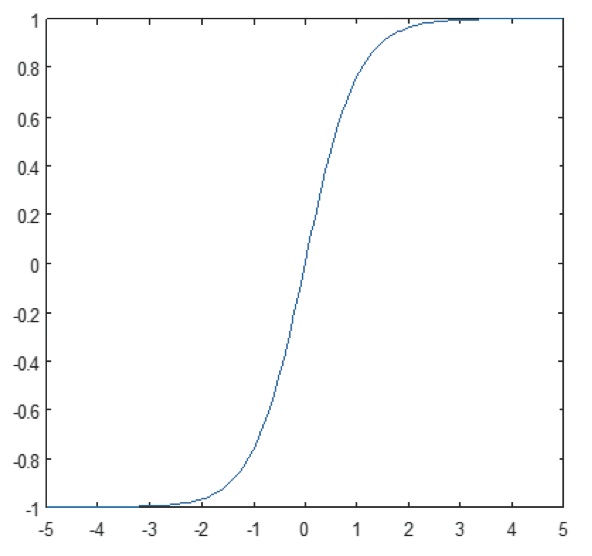
Figura 9: Grafico della funzione tangente iperbolica

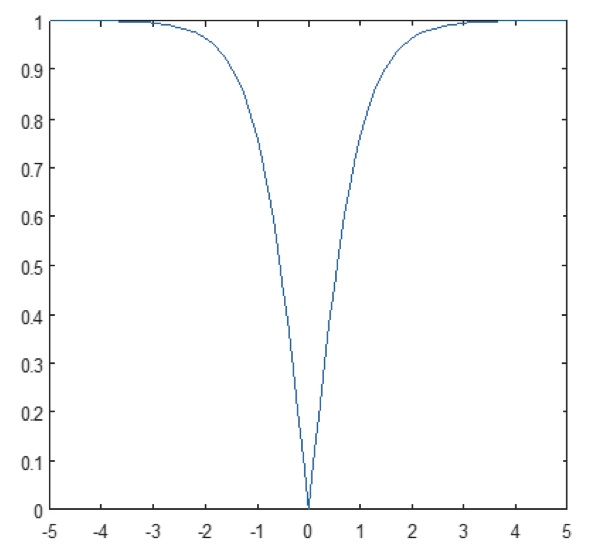
Figura 10: Grafico dell’assoluto della funzione tangente iperbolica

Figura 11: Grafico della funzione sigmoide

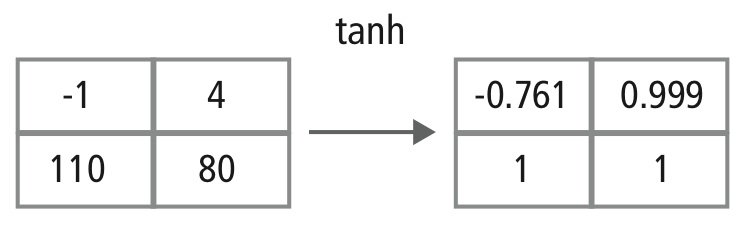
Figura 12: Rappresentazione pittorica dell’elaborazione di tanh

Strati completamente connessi

Gli strati completamente connessi sono spesso usati come gli strati finali di una CNN. Questi strati sommano matematicamente una ponderazione dello strato precedente di caratteristiche, indicando il mix preciso di “ingredienti” per determinare un risultato di output specifico. Nel caso di uno strato completamente connesso, tutti gli elementi di tutte le caratteristiche dello strato precedente vengono utilizzati nel calcolo di ogni elemento di ogni caratteristica di uscita.

La figura 13 spiega lo strato completamente connesso L. Lo strato L-1 ha due caratteristiche, ciascuna delle quali è 2×2, cioè ha quattro elementi. Lo strato L ha due caratteristiche, ognuna delle quali ha un singolo elemento.

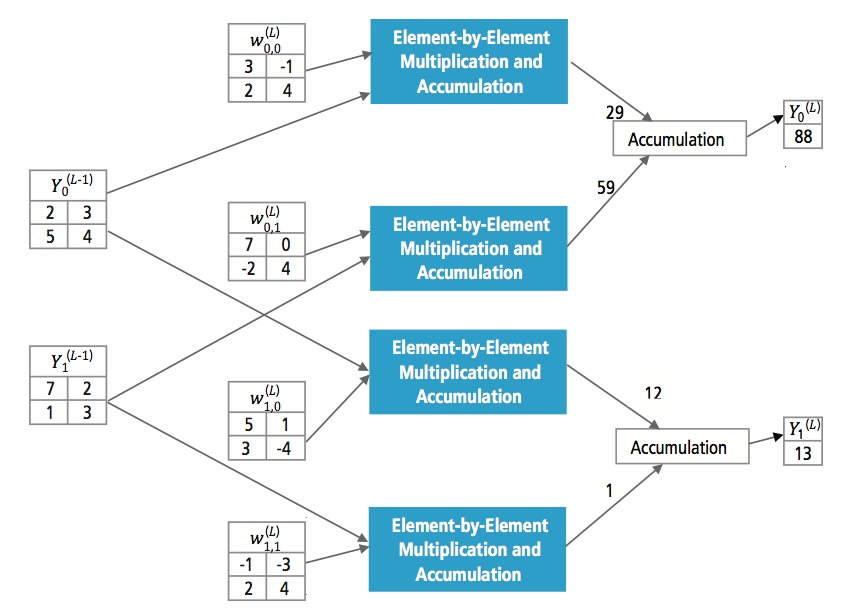
Figura 13: Elaborazione di uno strato completamente connesso

Perché CNN?

Mentre le reti neurali e altri metodi di rilevamento dei modelli esistono da 50 anni, nel recente passato c’è stato uno sviluppo significativo nel campo delle reti neurali convoluzionali. Questa sezione copre i vantaggi dell’uso di CNN per il riconoscimento delle immagini.

Resistenza a spostamenti e distorsioni nell’immagine

Il rilevamento tramite CNN è resistente a distorsioni come il cambiamento di forma dovuto all’obiettivo della fotocamera, diverse condizioni di illuminazione, diverse pose, presenza di occlusioni parziali, spostamenti orizzontali e verticali, ecc. Tuttavia, le CNN sono invarianti allo spostamento poiché la stessa configurazione dei pesi è usata in tutto lo spazio. In teoria, possiamo anche ottenere l’invarianza allo spostamento usando strati completamente connessi. Ma il risultato dell’addestramento in questo caso è costituito da più unità con modelli di peso identici in diverse posizioni dell’input. Per imparare queste configurazioni di peso, sarebbe necessario un gran numero di istanze di addestramento per coprire lo spazio delle possibili variazioni.

Meno requisiti di memoria

In questo stesso caso ipotetico in cui usiamo uno strato completamente connesso per estrarre le caratteristiche, l’immagine di ingresso di dimensioni 32×32 e uno strato nascosto con 1000 caratteristiche richiederà un ordine di 106 coefficienti, un enorme requisito di memoria. Nello strato convoluzionario, gli stessi coefficienti sono usati in diverse posizioni nello spazio, quindi il requisito di memoria è drasticamente ridotto.

Allenamento più facile e migliore

Anche usando la rete neurale standard che sarebbe equivalente a una CNN, poiché il numero di parametri sarebbe molto più alto, il tempo di allenamento aumenterebbe proporzionalmente. In una CNN, poiché il numero di parametri è drasticamente ridotto, il tempo di addestramento è proporzionalmente ridotto. Inoltre, assumendo un addestramento perfetto, possiamo progettare una rete neurale standard le cui prestazioni sarebbero le stesse di una CNN. Ma nell’addestramento pratico,
una rete neurale standard equivalente alla CNN avrebbe più parametri, il che porterebbe a una maggiore aggiunta di rumore durante il processo di addestramento. Quindi, le prestazioni di una rete neurale standard equivalente a una CNN saranno sempre più scarse.

Algoritmo di riconoscimento per il set di dati GTSRB

Il German Traffic Sign Recognition Benchmark (GTSRB) era una sfida di classificazione multiclasse e a immagine singola tenuta alla International Joint Conference on Neural Networks (IJCNN) 2011, con i seguenti requisiti:

• 51.840 immagini di segnali stradali tedeschi in 43 classi (Figure 14 e 15)
• Dimensione delle immagini varia da 15×15 a 222×193
• Le immagini sono raggruppate per classe e traccia con almeno 30 immagini per traccia
• Le immagini sono disponibili come immagini a colori (RGB), caratteristiche HOG, caratteristiche Haar, e istogrammi di colore
• La competizione è solo per l’algoritmo di classificazione; l’algoritmo per trovare la regione di interesse nel fotogramma non è richiesto
• Le informazioni temporali delle sequenze di test non sono condivise, quindi la dimensione temporale non può essere usata nell’algoritmo di classificazione

Figura 14: Segnali stradali ideali GTSRB

Figura 15: Segnali stradali GTSRB con problemi

Algoritmo Cadence per il riconoscimento dei segnali stradali nel dataset GTSRB

Cadence ha sviluppato vari algoritmi in MATLAB per il riconoscimento dei segnali stradali utilizzando il dataset GTSRB, partendo da una configurazione di base basata su un noto articolo sul riconoscimento dei segnali. Il tasso di rilevamento corretto del 99,24% e lo sforzo di calcolo di quasi >50 milioni di multipli-aggiunta per cartello è mostrato come un punto verde spesso nella Figura 16. Cadence ha raggiunto risultati significativamente migliori utilizzando il nostro nuovo approccio proprietario Hierarchical CNN. In questo algoritmo, 43 segnali stradali sono stati divisi in cinque famiglie. In totale, implementiamo sei CNN più piccole. La prima CNN decide a quale famiglia appartiene il segnale stradale ricevuto. Una volta che la famiglia del segnale è nota, la CNN (una delle cinque rimanenti) corrispondente alla famiglia individuata viene eseguita per decidere il segnale di traffico all’interno di quella famiglia. Utilizzando questo algoritmo, Cadence ha raggiunto un tasso di rilevamento corretto del 99,58%, il miglior CDR ottenuto su GTSRB fino ad oggi.

Algoritmo per il tradeoff tra prestazioni e complessità

Al fine di controllare la complessità delle CNN nelle applicazioni embedded, Cadence ha anche sviluppato un algoritmo proprietario utilizzando la decomposizione degli autovalori che riduce una CNN allenata alla sua dimensione canonica. Utilizzando questo algoritmo, siamo stati in grado di ridurre drasticamente la complessità della CNN senza alcuna degradazione delle prestazioni, o con una piccola riduzione controllata del CDR. La Figura 16 mostra i risultati ottenuti:

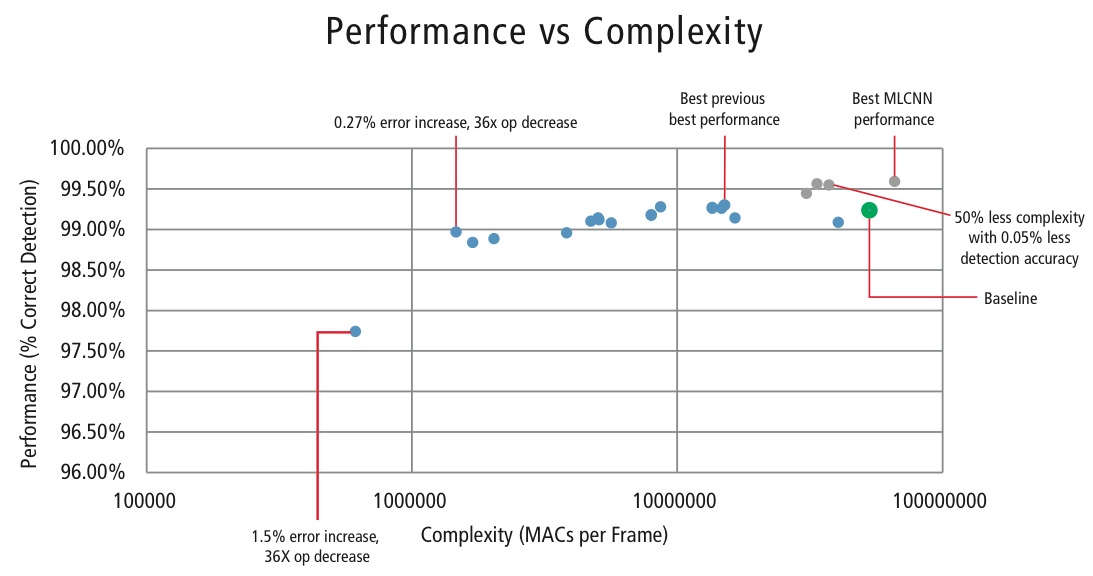
Figura 16: Grafico delle prestazioni vs. complessità per varie configurazioni CNN per rilevare i segnali stradali nel dataset GTSRB

Il punto verde nella Figura 16 è la configurazione di base. Questa configurazione è abbastanza vicina a quella suggerita in Reference . Richiede 53 MMACs per frame per un tasso di errore dello 0,76%.

• Il secondo punto da sinistra richiede 1,47 milioni di MACs per frame per un tasso di errore dell’1,03%, cioè, per un aumento del tasso di errore dello 0,27%, il requisito MAC è stato ridotto di un fattore di 36,14.
• Il punto più a sinistra richiede 0,61 MMAC per frame per ottenere un tasso di errore del 2,26%, cioè, il numero di MAC è ridotto di un fattore di 86,4 volte.
• I punti in blu sono per una CNN a livello singolo, mentre i punti in rosso sono per una CNN gerarchica. Una performance migliore del 99,58% è raggiunta dalla CNN gerarchica.

CNNs in Embedded Systems

Come mostrato nella Figura 5, un sottosistema di visione richiede un sacco di elaborazione delle immagini oltre a una CNN. Al fine di eseguire CNN su un sistema embedded a potenza limitata che supporta l’elaborazione delle immagini, dovrebbe soddisfare i seguenti requisiti:

• Disponibilità di alte prestazioni computazionali: Per una tipica implementazione CNN, miliardi di MAC al secondo è il requisito.
• Maggiore larghezza di banda load/store: nel caso di uno strato completamente connesso usato per la classificazione, ogni coefficiente viene usato nella moltiplicazione solo una volta. Quindi, il requisito di larghezza di banda load-store è maggiore del numero di MAC eseguiti dal processore.
• Richiesta di bassa potenza dinamica: Il sistema dovrebbe consumare meno energia. Per affrontare questo problema, è necessaria un’implementazione a virgola fissa, che impone il requisito di soddisfare i requisiti di prestazione usando il numero finito di bit minimo possibile.
• Flessibilità: Dovrebbe essere possibile aggiornare facilmente il progetto esistente a un nuovo progetto più performante.

Siccome le risorse computazionali sono sempre un vincolo nei sistemi embedded, se il caso d’uso permette una piccola degradazione delle prestazioni, è utile avere un algoritmo che possa ottenere un enorme risparmio nella complessità computazionale al costo di una piccola degradazione controllata delle prestazioni. Quindi, il lavoro di Cadence su un algoritmo per ottenere un compromesso tra complessità e prestazioni, come spiegato nella sezione precedente, ha grande rilevanza per l’implementazione di CNN su sistemi embedded.

CNN su processori Tensilica

Il DSP Tensilica Vision P5 è un DSP ad alte prestazioni e bassa potenza progettato specificamente per l’elaborazione di immagini e visione artificiale. Il DSP ha un’architettura VLIW con supporto SIMD. Ha cinque slot di emissione in una parola di istruzione fino a 96 bit e può caricare fino a 1024 bit di parole dalla memoria ogni ciclo. I registri interni e le unità operative vanno da 512 bit a 1536 bit, dove i dati sono rappresentati come 16, 32, o 64 fette di 8b, 16b, 24b, 32b, o 48b pixel.

Il DSP affronta tutte le sfide per implementare le CNN nei sistemi embedded come discusso nella sezione precedente.

• Disponibilità di alte prestazioni computazionali: Oltre al supporto avanzato per l’implementazione dell’elaborazione del segnale di immagine, il DSP ha il supporto delle istruzioni per tutte le fasi delle CNN. Per le operazioni di convoluzione, ha un set di istruzioni molto ricco che supporta operazioni di moltiplicazione/moltiplicazione-accumulazione che supportano operazioni 8b x 8b, 8b x 16b e 16b x 16b per dati firmati/non firmati. Può eseguire fino a 64 operazioni di moltiplicazione/moltiplicazione-accumulazione 8b x 16b e 8b x 8b in un ciclo e 32 operazioni di moltiplicazione/moltiplicazione-accumulazione 16b x 16b in un ciclo. Per il max pooling e la funzionalità ReLU, il DSP ha istruzioni per fare 64 confronti a 8 bit in un ciclo. Per implementare funzioni non lineari con intervalli finiti come tanh e signum, ha istruzioni per implementare una tabella di look-up per 64 valori a 7 bit in un ciclo. Nella maggior parte dei casi, le istruzioni per il confronto e la tabella di look-up sono programmate in parallelo con le istruzioni di moltiplicazione/moltiplicazione-accumulazione e non richiedono alcun ciclo extra.
• Banda passante più ampia: il DSP può eseguire fino a due operazioni di load/store a 512 bit per ciclo.
• Basso requisito di potenza dinamica: Il DSP è una macchina a punto fisso. Grazie alla gestione flessibile di una varietà di tipi di dati, la piena prestazione e il vantaggio energetico del calcolo misto a 16b e 8b possono essere raggiunti con una minima perdita di precisione.
• Flessibilità: Poiché il DSP è un processore programmabile, il sistema può essere aggiornato a una nuova versione semplicemente eseguendo un aggiornamento del firmware.
• Floating Point: Per gli algoritmi che richiedono una gamma dinamica estesa per i loro dati e/o coefficienti, il DSP ha un’unità opzionale in virgola mobile vettoriale.

Il DSP Vision P5 viene fornito con un set completo di strumenti software che comprende un compilatore C/C++ ad alte prestazioni con vettorizzazione e programmazione automatica per supportare l’architettura SIMD e VLIW senza la necessità di scrivere il linguaggio assembly. Questo set di strumenti completo include anche il linker, l’assemblatore, il debugger, il profiler e gli strumenti di visualizzazione grafica. Un completo simulatore di set di istruzioni (ISS) permette al progettista di simulare e valutare rapidamente le prestazioni. Quando si lavora con sistemi di grandi dimensioni o vettori di prova lunghi, l’opzione del simulatore TurboXim, veloce e funzionale, raggiunge velocità da 40 a 80 volte superiori a quelle dell’ISS per un efficiente sviluppo del software e una verifica funzionale.

Cadence ha implementato un’architettura CNN a strato singolo sul DSP per il riconoscimento dei segnali stradali tedeschi. Cadence ha raggiunto un CDR del 99,403% con quantizzazione a 16 bit per i campioni di dati e quantizzazione a 8 bit per i coefficienti in tutti gli strati per questa architettura. Ha due strati di convoluzione, tre strati completamente connessi, quattro strati ReLU, tre strati di max pooling e uno strato non lineare tanh. Cadence ha raggiunto una performance di 38,58 MAC/ciclo in media per la rete completa, compresi i cicli per tutti gli strati max pooling, tanh e ReLU. Cadence ha raggiunto le prestazioni del caso migliore di 58,43 MAC per ciclo per il terzo strato, compresi i cicli per le funzionalità tanh e ReLU. Questo DSP che gira a 600MHz può elaborare più di 850 segnali stradali in un secondo.

Il futuro delle CNN

Tra le aree promettenti della ricerca sulle reti neurali ci sono le reti neurali ricorrenti (RNN) che utilizzano la memoria a lungo termine (LSTM). Queste aree stanno fornendo l’attuale stato dell’arte nei compiti di riconoscimento delle serie temporali come il riconoscimento del parlato e della scrittura. RNN/autocodificatori sono anche in grado di generare scrittura a mano/parlato/immagini con alcune distribuzioni note ,,,,.

Le reti di credenza profonde, un altro promettente tipo di rete che utilizza macchine di Boltzman ristrette (RMB)/autocodificatori, sono in grado di essere addestrate avidamente, uno strato alla volta, e quindi sono più facilmente addestrabili per reti molto profonde,.

Conclusione

Le CNN danno le migliori prestazioni nei problemi di riconoscimento di pattern/immagini e superano persino gli umani in alcuni casi. Cadence ha ottenuto i migliori risultati del settore utilizzando algoritmi e architetture proprietarie con le CNN. Abbiamo sviluppato CNN gerarchiche per il riconoscimento dei segnali stradali nel GTSRB, ottenendo le migliori prestazioni di sempre su questo set di dati. Abbiamo sviluppato un altro algoritmo per il tradeoff performance-versus-complexity e siamo stati in grado di ottenere una riduzione della complessità di un fattore 86 per una degradazione del CDR inferiore al 2%. Il DSP Tensilica Vision P5 per l’imaging e la computer vision di Cadence ha tutte le caratteristiche necessarie per implementare le CNN oltre a quelle necessarie per l’elaborazione dei segnali di immagine. Più di 850 riconoscimenti di segnali stradali possono essere eseguiti eseguendo il DSP a 600MHz. Il DSP Tensilica Vision P5 di Cadence ha un set di caratteristiche quasi ideale per eseguire CNN.

“Rete neurale artificiale”. Wikipedia. https://en.wikipedia.org/wiki/Artificial_neural_network

Karpathy, Andrej. 2015. “Reti neurali parte 1: impostazione dell’architettura”. Appunti per CS231n Convolutional Neural Networks for Visual Recognition, Stanford University. http://cs231n.github.io/neural-networks-1/

“Rete neurale convoluzionale.” Wikipedia. https://en.wikipedia.org/wiki/Convolutional_neural_network

Sermanet, Pierre, e Yann LeCun. 2011. “Riconoscimento della segnaletica stradale con reti multi-scala”. Courant Institute of Mathematical Sciences, New York University. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6033589

Ciresan, Dan, Ueli Meier, e Jürgen Schmidhuber. 2012. “Reti neurali profonde a più colonne per la classificazione delle immagini. 2012 IEEE Conference on Computer Vision and Pattern Recognition (New York, NY: Institute of Electrical and Electronics Engineers (IEEE)). http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6248110

Ciresan, Dan, Ueli Meier, Jonathan Masci, Luca M. Gambardella, e Jurgen Schmidhuber. 2011. “Reti neurali convoluzionali flessibili e ad alte prestazioni per la classificazione delle immagini”. Atti della Ventiduesima Conferenza Internazionale Congiunta sull’Intelligenza Artificiale-Volume Due: 1237-1242. Recuperato il 17 novembre 2013. http://people.idsia.ch/~juergen/ijcai2011.pdf

Lawrence, Steve, C. Lee Giles, Ah Chung Tsoi, e Andrew D. Back. 1997. “Riconoscimento dei volti: A Convolutional Neural Network Approach”. IEEE Transactions on Neural Networks, Volume 8; Issue 1. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=554195

Russakovsky, O. et al. 2014. “ImageNet Large Scale Visual Recognition Challenge”. International Journal of Computer Vision. http://link.springer.com/article/10.1007/s11263-015-0816-y#

Ovtcharov, Kalin, Olatunji Ruwarse, Joo-Young Kim et al. 22 feb 2015. “Accelerare le reti convoluzionali profonde usando un hardware specializzato”. Microsoft Research. http://research-srv.microsoft.com/pubs/240715/CNN%20Whitepaper.pdf

Stallkamp, J., M. Schlipsing, J. Salmen, e C. Igel. “L’uomo contro il computer: Benchmarking Machine Learning Algorithms For Traffic Sign Application”. IJCNN 2011. http://www.sciencedirect.com/science/article/pii/S0893608012000457

Hochreiter, Sepp, e Jürgen Schmidhuber. 1997. “Memoria lunga a breve termine”. Neural Computation, 9(8):1735-1780. ftp://ftp.idsia.ch/pub/juergen/lstm.pdf

Graves, Alex. 2014. “Generazione di sequenze con reti neurali ricorrenti”. http://arxiv.org/abs/1308.0850

Schmidhuber, Jurgen. 2015. “Reti neurali ricorrenti”. http://people.idsia.ch/~juergen/rnn.html

Olshausen, Bruno A., e David J. Field. 1996. “Emergenza delle proprietà del campo recettivo delle cellule semplici con l’apprendimento di un codice sparso per le immagini naturali”. Nature 381.6583: 607-609. http://www.nature.com/nature/journal/v381/n6583/abs/381607a0.html

Hinton, G. E. e Salakhutdinov, R. R. 2006. “Ridurre la dimensionalità dei dati con le reti neurali”. Science vol. 313 no. 5786 pp. 504-507. http://www.sciencemag.org/content/suppl/2006/08/04/313.5786.504.DC1.

Hinton, Geoffrey E. 2009. “Reti di credenza profonde”. Scholarpedia, 4(5):5947.
http://www.scholarpedia.org/article/Deep_belief_networks