Medie mobili in pandas

Introduzione
Una media mobile, chiamata anche media mobile o corrente, è usata per analizzare i dati delle serie temporali calcolando le medie di diversi sottoinsiemi del set di dati completo. Poiché si tratta di prendere la media della serie di dati nel tempo, viene anche chiamata media mobile (MM) o media mobile.
Ci sono vari modi in cui la media mobile può essere calcolata, ma uno di questi modi è quello di prendere un sottoinsieme fisso da una serie completa di numeri. La prima media mobile viene calcolata facendo la media del primo sottoinsieme fisso di numeri, e poi il sottoinsieme viene cambiato passando al successivo sottoinsieme fisso (includendo il valore futuro nel sottogruppo mentre si esclude il numero precedente dalla serie).
La media mobile viene usata principalmente con dati di serie temporali per catturare le fluttuazioni a breve termine mentre ci si concentra sulle tendenze più lunghe.
Alcuni esempi di dati di serie temporali possono essere i prezzi delle azioni, i rapporti meteorologici, la qualità dell’aria, il prodotto interno lordo, l’occupazione, ecc.
In generale, la media mobile smussa i dati.
La media mobile è la spina dorsale di molti algoritmi, e uno di questi algoritmi è l’Autoregressive Integrated Moving Average Model (ARIMA), che usa le medie mobili per fare previsioni sui dati delle serie temporali.
Ci sono vari tipi di medie mobili:
-
Simple Moving Average (SMA): La media mobile semplice (SMA) usa una finestra scorrevole per prendere la media su un numero stabilito di periodi di tempo. È una media equamente ponderata degli n dati precedenti.
Per capire meglio la SMA, prendiamo un esempio, una sequenza di n valori:

allora la media mobile equamente pesata per n punti dati sarà essenzialmente la media dei precedenti M punti dati, dove M è la dimensione della finestra scorrevole:

Similmente, per calcolare i successivi valori di media mobile, un nuovo valore sarà aggiunto alla somma, e il valore del periodo di tempo precedente sarà eliminato, poiché si ha la media dei periodi di tempo precedenti, quindi non è richiesta la somma completa ogni volta:

- Media mobile cumulativa (CMA): A differenza della media mobile semplice che elimina l’osservazione più vecchia quando viene aggiunta quella nuova, la media mobile cumulativa considera tutte le osservazioni precedenti. La CMA non è una tecnica molto buona per analizzare le tendenze e smussare i dati. La ragione è che fa la media di tutti i dati precedenti fino al punto corrente, quindi una media equamente ponderata della sequenza di n valori:



- Media mobile esponenziale (EMA): A differenza di SMA e CMA, la media mobile esponenziale dà più peso ai prezzi recenti e di conseguenza, può essere un modello migliore o catturare meglio il movimento della tendenza in modo più veloce. La reazione dell’EMA è direttamente proporzionale al modello dei dati.
Siccome le EMA danno un peso maggiore ai dati recenti che a quelli più vecchi, sono più reattive alle ultime variazioni di prezzo rispetto alle SMA, il che rende i risultati delle EMA più tempestivi e quindi le EMA sono preferite ad altre tecniche.
Basta con la teoria, giusto? Saltiamo all’implementazione pratica della media mobile.
Implementazione della media mobile su dati di serie temporali
Media mobile semplice (SMA)
Prima di tutto, creiamo dei dati di serie temporali fittizi e proviamo ad implementare la SMA usando solo Python.
Assumiamo che ci sia una domanda per un prodotto e che sia osservata per 12 mesi (1 anno), e che tu abbia bisogno di trovare medie mobili per periodi di 3 e 4 mesi.
Modulo di importazione
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| mese | domanda | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Calcoliamo la SMA per una finestra di dimensioni 3, il che significa che si considereranno tre valori ogni volta per calcolare la media mobile, e per ogni nuovo valore, il valore più vecchio sarà ignorato.
Per implementare questo, userai la funzione pandas iloc, poiché la colonna demand è ciò di cui hai bisogno, fisserai la posizione di quella nella funzione iloc mentre la riga sarà una variabile i che continuerai a iterare fino a raggiungere la fine del dataframe.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| mese | domanda | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Per un controllo di sanità mentale, usiamo anche la funzione pandas incorporata rolling e vediamo se corrisponde alla nostra media mobile semplice basata su python.
df = df.iloc.rolling(window=3).mean()df.head()| mese | domanda | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Fico, quindi come puoi vedere, le medie mobili personalizzate e quelle di pandas corrispondono esattamente, il che significa che la tua implementazione della SMA era corretta.
Calcoliamo anche rapidamente la media mobile semplice per un window_size di 4.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| mese | domanda | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| mese | domanda | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 | 289.5 |
Ora, traccerai i dati delle medie mobili che hai calcolato.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>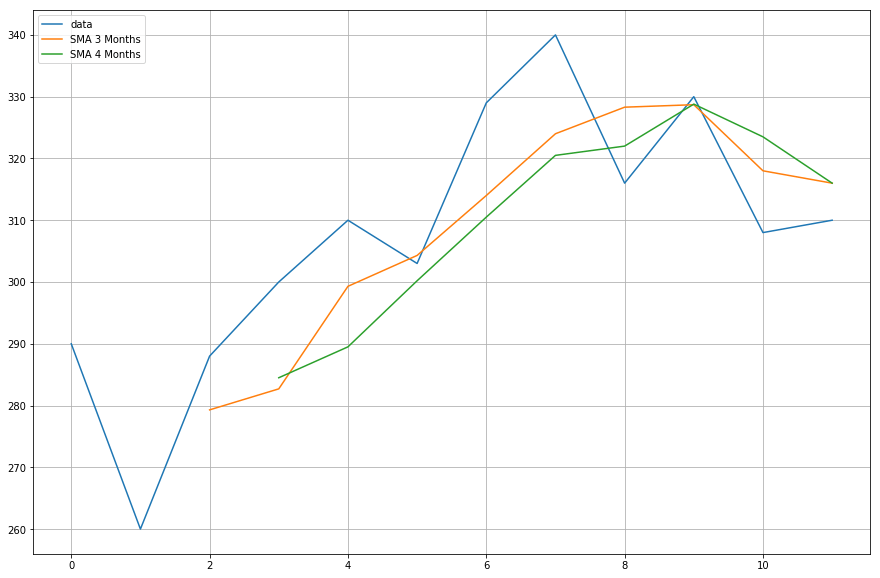
Media mobile cumulativa
Penso che ora siamo pronti per passare a un set di dati reale.
Per la media mobile cumulativa, usiamo un air quality dataset che può essere scaricato da questo link.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Date | Time | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
La pre-elaborazione è un passo essenziale quando si lavora con dati. Per i dati numerici uno dei passi di pre-elaborazione più comuni è quello di controllare i valori NaN (Null). Se ci sono dei valori NaN, potete sostituirli con 0 o con la media o con i valori precedenti o successivi o anche abbandonarli. Anche se la sostituzione è normalmente una scelta migliore rispetto all’eliminazione, dato che questo set di dati ha pochi valori NULL, l’eliminazione non influenzerà la continuità della serie.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Dall’output di cui sopra, si può osservare che ci sono circa 114 valori NaN in tutte le colonne, tuttavia si può capire che sono tutti alla fine della serie temporale, quindi eliminiamoli rapidamente.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Applicherete la media mobile cumulativa sulla Temperature column (T), quindi separiamo rapidamente quella colonna dai dati completi.
df_T = pd.DataFrame(df.iloc)df_T.head()
Ora, userete il metodo pandas expanding per trovare la media cumulativa dei dati di cui sopra. Se ricordate dall’introduzione, a differenza della media mobile semplice, la media mobile cumulativa considera tutti i valori precedenti quando calcola la media.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
I dati delle serie temporali vengono tracciati rispetto al tempo, quindi combiniamo la colonna della data e del tempo e convertiamoli in un oggetto datetime. Per ottenere questo, useremo il modulo datetime di python (Fonte: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Cambiamo l’indice del dataframe temperature con datetime.
df_T.index = df.DateTimeTracciamo ora la temperatura attuale e la media mobile cumulativa rispetto al tempo.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Media mobile esponenziale
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DateTime | |||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>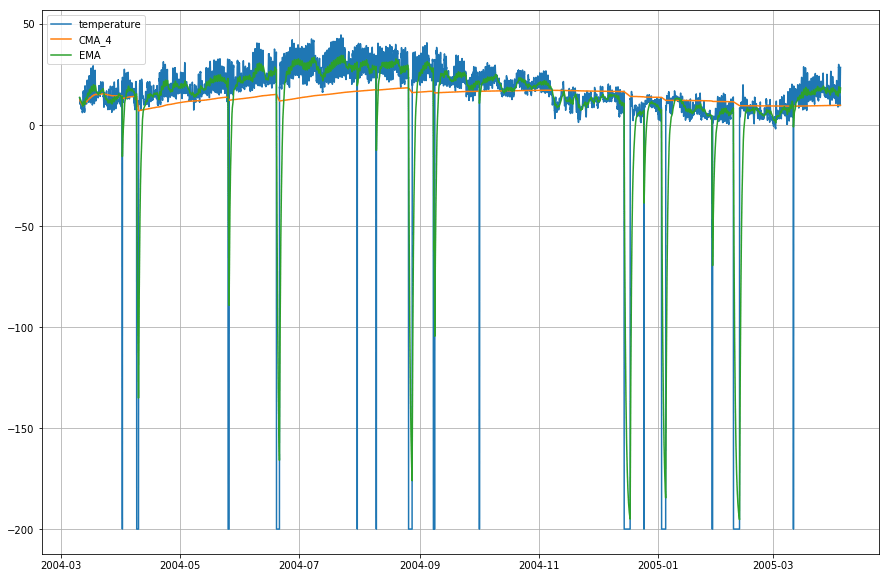
Wow! Quindi, come puoi osservare dal grafico qui sopra, che il Exponential Moving Average (EMA) fa un lavoro superbo nel catturare il modello dei dati mentre il Cumulative Moving Average (CMA) manca di un margine considerevole.
Vai oltre!
Congratulazioni per aver finito il tutorial.
Questo tutorial è stato un buon punto di partenza su come puoi calcolare le medie mobili dei tuoi dati e dargli un senso.
Prova a scrivere il codice python delle medie mobili cumulative ed esponenziali senza usare la libreria pandas. Questo vi darà una conoscenza molto più approfondita su come vengono calcolate e in quali modi sono diverse l’una dall’altra.
C’è ancora molto da sperimentare. Provate a calcolare l’autocorrelazione parziale tra i dati di input e la media mobile, e cercate di trovare qualche relazione tra i due.
Se volete saperne di più su DataFrames in pandas, seguite il corso interattivo pandas Foundations di DataCamp.