De-Multiplexer è un circuito combinazionale che esegue l’operazione inversa del Multiplexer. Ha un singolo ingresso, ‘n’ linee di selezione e un massimo di 2n uscite. L’ingresso sarà collegato a una di queste uscite in base ai valori delle linee di selezione.

Siccome ci sono ‘n’ linee di selezione, ci saranno 2n possibili combinazioni di zero e uno. Quindi, ogni combinazione può selezionare solo un’uscita. Il De-Multiplexer è anche chiamato De-Mux.

1×4 De-Multiplexer

1×4 De-Multiplexer ha un ingresso I, due linee di selezione, s1 & s0 e quattro uscite Y3, Y2, Y1 &Y0. Lo schema a blocchi del 1×4 De-Multiplexer è mostrato nella figura seguente.

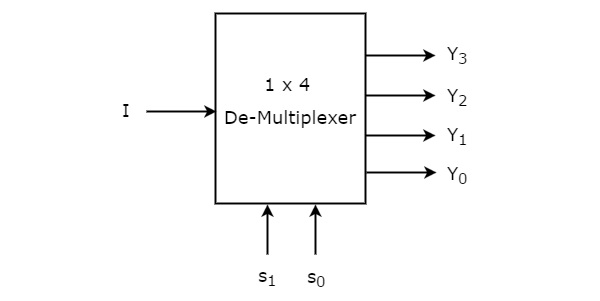
Il singolo ingresso ‘I’ sarà collegato a una delle quattro uscite, da Y3 a Y0 in base ai valori delle linee di selezione s1 & s0. La tabella della verità del De-Multiplexer 1×4 è mostrata qui sotto.

Ingressi di selezione		Uscite
S1	S0	Y3	Y2	Y1	Y0
0	0	0	0	0	I
0	1	0	0	I	0
1	0	0	I	0	0
1	1	I	0	0	0

Dalla precedente tabella della verità, possiamo scrivere direttamente le funzioni booleane per ogni uscita come

$Y_{3}=s_{1}s_{0}I$$

$Y_{2}=s_{1}{s_{0}}’I$$

$Y_{1}={s_{1}}’s_{0}I$$

$Y_{0}={s_1}'{s_{0}}’I$$

Possiamo implementare queste funzioni booleane usando Invertitori &3porte AND a 3 ingressi. Lo schema del circuito del De-Multiplexer 1×4 è mostrato nella figura seguente.

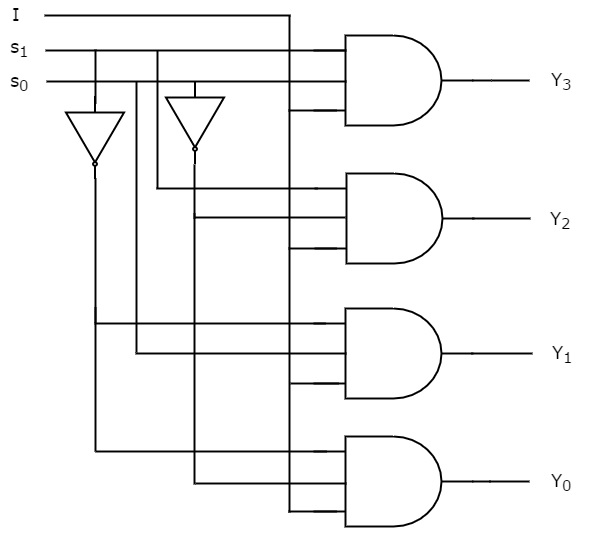
Possiamo facilmente capire il funzionamento del circuito di cui sopra. Allo stesso modo, è possibile implementare il De-Multiplexer 1×8 e il De-Multiplexer 1×16 seguendo la stessa procedura.

Implementazione di De-Multiplexer di ordine superiore

Ora, implementiamo i seguenti due De-Multiplexer di ordine superiore usando De-Multiplexer di ordine inferiore.

• 1×8 De-Multiplexer
• 1×16 De-Multiplexer

1×8 De-Multiplexer

In questa sezione, implementiamo 1×8 De-Multiplexer usando 1×4 De-Multiplexer e 1×2 De-Multiplexer. Sappiamo che il De-Multiplexer 1×4 ha un singolo ingresso, due linee di selezione e quattro uscite. Mentre, il De-Multiplexer 1×8 ha un singolo ingresso, tre linee di selezione e otto uscite.

Quindi, abbiamo bisogno di due De-Multiplexer 1×4 nel secondo stadio per ottenere le otto uscite finali. Poiché il numero di ingressi nel secondo stadio è due, abbiamo bisogno di 1×2 DeMultiplexer nel primo stadio in modo che le uscite del primo stadio siano gli ingressi del secondo stadio. L’ingresso di questo 1×2 De-Multiplexer sarà l’ingresso complessivo del 1×8 De-Multiplexer.

Lasciamo che il 1×8 De-Multiplexer abbia un ingresso I, tre linee di selezione s2, s1 & s0 e uscite Y7 a Y0. La tabella della verità del 1×8 De-Multiplexer è mostrata qui sotto.

ingressi di selezione			uscite
s2	s1	s0	Y7	Y6	Y5	Y4	Y3	Y2	Y1	Y0
0	0	0	0	0	0	0	0	0	0	0	I
0	0	1	0	0	0	0	0	0	I	0
0	1	0	0	0	0	0	0	I	0	0
0	1	1	0	0	0	0	I	0	0	0
1	0	0	0	0	0	I	0	0	0	0
1	0	1	0	0	I	0	0	0	0	0
1	1	0	0	I	0	0	0	0	0	0
1	1	1	I	0	0	0	0	0	0	0

Possiamo implementare 1×8 De-Multiplexer usando multiplexer di ordine inferiore facilmente considerando la tabella di verità di cui sopra. Lo schema a blocchi del 1×8 De-Multiplexer è mostrato nella figura seguente.

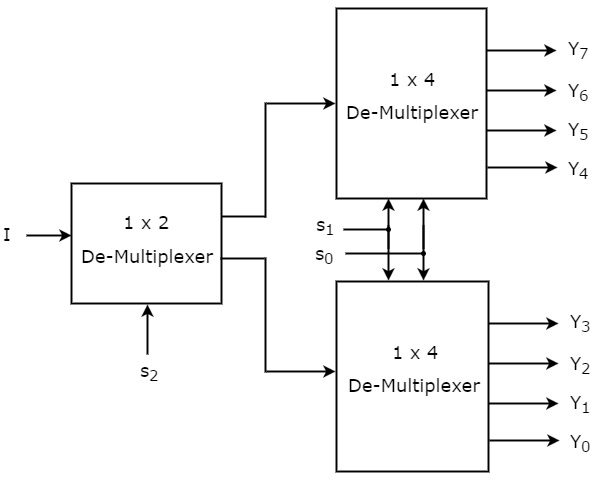
Le linee di selezione comuni, s1 & s0 sono applicate a entrambi i De-Multiplexer 1×4. Le uscite del De-Multiplexer 1×4 superiore sono da Y7 a Y4 e le uscite del De-Multiplexer 1×4 inferiore sono da Y3 a Y0.

L’altra linea di selezione, s2 è applicata al De-Multiplexer 1×2. Se s2 è zero, allora una delle quattro uscite del De-Multiplexer 1×4 inferiore sarà uguale all’ingresso, I basato sui valori delle linee di selezione s1 & s0. Allo stesso modo, se s2 è uno, allora una delle quattro uscite del De-Multiplexer 1×4 superiore sarà uguale all’ingresso, I in base ai valori delle linee di selezione s1 & s0.

1×16 De-Multiplexer

In questa sezione, implementiamo 1×16 De-Multiplexer usando 1×8 De-Multiplexer e 1×2 De-Multiplexer. Sappiamo che il 1×8 De-Multiplexer ha un singolo ingresso, tre linee di selezione e otto uscite. Mentre, il 1×16 De-Multiplexer ha un singolo ingresso, quattro linee di selezione e sedici uscite.

Quindi, abbiamo bisogno di due 1×8 De-Multiplexer nel secondo stadio per ottenere le sedici uscite finali. Poiché il numero di ingressi nel secondo stadio è due, abbiamo bisogno di 1×2 DeMultiplexer nel primo stadio in modo che le uscite del primo stadio siano gli ingressi del secondo stadio. L’ingresso di questo 1×2 De-Multiplexer sarà l’ingresso complessivo del 1×16 De-Multiplexer.

Il 1×16 De-Multiplexer ha un ingresso I, quattro linee di selezione s3, s2, s1 & s0 e uscite Y15 a Y0. Lo schema a blocchi del 1×16 De-Multiplexer usando multiplexer di ordine inferiore è mostrato nella figura seguente.

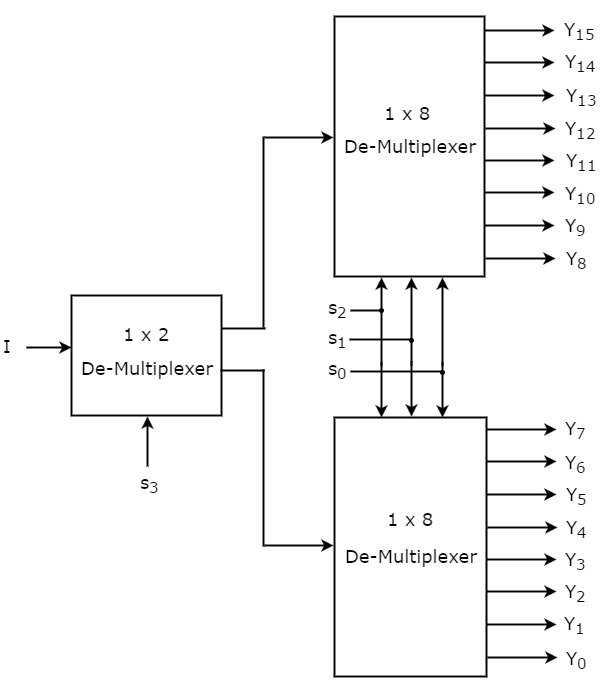
Le linee di selezione comuni s2, s1 & s0 sono applicate a entrambi i De-Multiplexer 1×8. Le uscite del De-Multiplexer 1×8 superiore sono da Y15 a Y8 e le uscite del DeMultiplexer 1×8 inferiore sono da Y7 a Y0.

L’altra linea di selezione, s3 è applicata al De-Multiplexer 1×2. Se s3 è zero, allora una delle otto uscite del De-Multiplexer 1×8 inferiore sarà uguale all’ingresso, I basato sui valori delle linee di selezione s2, s1 & s0. Allo stesso modo, se s3 è uno, allora una delle 8 uscite del De-Multiplexer 1×8 superiore sarà uguale all’ingresso, I in base ai valori delle linee di selezione s2, s1 & s0.