Gleitende Durchschnitte in Pandas

Einführung
Ein gleitender Durchschnitt, auch gleitender oder laufender Durchschnitt genannt, wird zur Analyse von Zeitreihendaten verwendet, indem Durchschnitte verschiedener Teilmengen des gesamten Datensatzes berechnet werden. Da es sich um den Durchschnitt des Datensatzes über die Zeit handelt, wird er auch als gleitender Mittelwert (MM) oder rollender Mittelwert bezeichnet.
Es gibt verschiedene Möglichkeiten, wie der gleitende Mittelwert berechnet werden kann, aber eine davon ist, eine feste Teilmenge aus einer vollständigen Zahlenreihe zu nehmen. Der erste gleitende Durchschnitt wird berechnet, indem die erste feste Teilmenge von Zahlen gemittelt wird, und dann wird die Teilmenge geändert, indem man zur nächsten festen Teilmenge übergeht (wobei der zukünftige Wert in die Teilgruppe aufgenommen wird, während die vorherige Zahl aus der Reihe ausgeschlossen wird).
Der gleitende Durchschnitt wird meist bei Zeitreihendaten verwendet, um die kurzfristigen Schwankungen zu erfassen, während man sich auf längere Trends konzentriert.
Ein paar Beispiele für Zeitreihendaten können Aktienkurse, Wetterberichte, Luftqualität, Bruttoinlandsprodukt, Beschäftigung usw. sein.
Im Allgemeinen glättet der gleitende Durchschnitt die Daten.
Der gleitende Durchschnitt ist das Rückgrat vieler Algorithmen, und einer dieser Algorithmen ist das Autoregressive Integrated Moving Average Model (ARIMA), das gleitende Durchschnitte verwendet, um Vorhersagen über Zeitreihendaten zu machen.
Es gibt verschiedene Arten von gleitenden Durchschnitten:
-
Simple Moving Average (SMA): Der einfache gleitende Durchschnitt (SMA) verwendet ein gleitendes Fenster, um den Durchschnitt über eine bestimmte Anzahl von Zeiträumen zu bilden. Er ist ein gleich gewichteter Mittelwert der letzten n Daten.
Um den SMA besser zu verstehen, nehmen wir ein Beispiel, eine Folge von n Werten:

Dann ist der gleich gewichtete gleitende Durchschnitt für n Datenpunkte im Wesentlichen der Mittelwert der vorherigen M Datenpunkte, wobei M die Größe des gleitenden Fensters ist:

Auch bei der Berechnung aufeinanderfolgender gleitender Durchschnittswerte wird ein neuer Wert zur Summe hinzugefügt und der Wert des vorherigen Zeitraums herausgenommen, da man den Durchschnitt der vorherigen Zeiträume hat, so dass nicht jedes Mal eine vollständige Summierung erforderlich ist:

- Kumulativer gleitender Durchschnitt (CMA): Im Gegensatz zum einfachen gleitenden Durchschnitt, der die älteste Beobachtung fallen lässt, wenn eine neue hinzukommt, berücksichtigt der kumulative gleitende Durchschnitt alle früheren Beobachtungen. Der kumulative gleitende Durchschnitt ist keine sehr gute Technik zur Analyse von Trends und zur Glättung der Daten. Der Grund dafür ist, dass alle früheren Daten bis zum aktuellen Datenpunkt gemittelt werden, also ein gleich gewichteter Durchschnitt der Folge von n Werten:



- Exponentieller gleitender Durchschnitt (EMA): Im Gegensatz zu SMA und CMA wird beim exponentiellen gleitenden Durchschnitt den jüngsten Kursen mehr Gewicht beigemessen, was dazu führt, dass er ein besseres Modell ist oder die Bewegung des Trends schneller erfasst. Die Reaktion des EMA ist direkt proportional zu dem Muster der Daten.
Da EMAs die jüngsten Daten stärker gewichten als ältere Daten, reagieren sie im Vergleich zu SMAs stärker auf die jüngsten Kursveränderungen, wodurch die Ergebnisse von EMAs zeitnaher sind und daher EMAs gegenüber anderen Techniken bevorzugt werden.
Genug der Theorie, oder? Kommen wir zur praktischen Implementierung des gleitenden Durchschnitts.
Implementierung des gleitenden Durchschnitts bei Zeitreihendaten
Einfacher gleitender Durchschnitt (SMA)
Zunächst erstellen wir Dummy-Zeitreihendaten und versuchen, den SMA nur mit Python zu implementieren.
Angenommen, es gibt eine Nachfrage nach einem Produkt, die über 12 Monate (1 Jahr) beobachtet wird, und Sie müssen gleitende Durchschnitte für Zeiträume von 3 und 4 Monaten finden.
Importmodul
import pandas as pdimport numpy as npproduct = {'month' : ,'demand':}df = pd.DataFrame(product)df.head()| Monat | Bedarf | |
|---|---|---|
| 0 | 1 | 290 |
| 1 | 2 | 260 |
| 2 | 3 | 288 |
| 3 | 4 | 300 |
| 4 | 5 | 310 |
Lassen Sie uns SMA für eine Fenstergröße von 3 berechnen, Das bedeutet, dass bei der Berechnung des gleitenden Durchschnitts jedes Mal drei Werte berücksichtigt werden, und bei jedem neuen Wert wird der älteste Wert ignoriert.
Um dies zu implementieren, verwenden Sie die Funktion iloc von Pandas, da die Spalte demand das ist, was Sie brauchen, legen Sie die Position dieser in der Funktion iloc fest, während die Zeile eine Variable i sein wird, die Sie solange iterieren, bis Sie das Ende des Datenrahmens erreichen.
for i in range(0,df.shape-2): df.loc,'SMA_3'] = np.round(((df.iloc+ df.iloc +df.iloc)/3),1)df.head()| Monat | Nachfrage | SMA_3 | |
|---|---|---|---|
| 0 | 1 | 290 | NaN |
| 1 | 2 | 260 | NaN |
| 2 | 3 | 288 | 279.3 |
| 3 | 4 | 300 | 282.7 |
| 4 | 5 | 310 | 299.3 |
Zur Überprüfung der Richtigkeit verwenden wir auch die pandas eingebaute rolling Funktion und sehen, ob sie mit unserem benutzerdefinierten, auf Python basierenden einfachen gleitenden Durchschnitt übereinstimmt.
df = df.iloc.rolling(window=3).mean()df.head()| Monat | Nachfrage | SMA_3 | pandas_SMA_3 | |
|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN |
| 1 | 2 | 2 | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 |
| 3 | 4 | 300 | 282.7 | 282.666667 |
| 4 | 5 | 310 | 299.3 | 299.333333 |
Cool, wie Sie sehen, stimmen die benutzerdefinierten und die gleitenden Durchschnitte von Pandas genau überein, was bedeutet, dass Ihre Implementierung des SMA korrekt war.
Lassen Sie uns auch schnell den einfachen gleitenden Durchschnitt für einen window_size von 4 berechnen.
for i in range(0,df.shape-3): df.loc,'SMA_4'] = np.round(((df.iloc+ df.iloc +df.iloc+df.iloc)/4),1)df.head()| Monat | Nachfrage | SMA_3 | pandas_SMA_3 | SMA_4 | |
|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 |
df = df.iloc.rolling(window=4).mean()df.head()| Monat | Nachfrage | SMA_3 | pandas_SMA_3 | SMA_4 | pandas_SMA_4 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 290 | NaN | NaN | NaN | NaN |
| 1 | 2 | 260 | NaN | NaN | NaN | NaN |
| 2 | 3 | 288 | 279.3 | 279.333333 | NaN | NaN |
| 3 | 4 | 300 | 282.7 | 282.666667 | 284.5 | 284.5 |
| 4 | 5 | 310 | 299.3 | 299.333333 | 289.5 | 289.5 |
Nun stellst du die Daten der von dir berechneten gleitenden Durchschnitte dar.
import matplotlib.pyplot as plt%matplotlib inlineplt.figure(figsize=)plt.grid(True)plt.plot(df,label='data')plt.plot(df,label='SMA 3 Months')plt.plot(df,label='SMA 4 Months')plt.legend(loc=2)<matplotlib.legend.Legend at 0x11fe15080>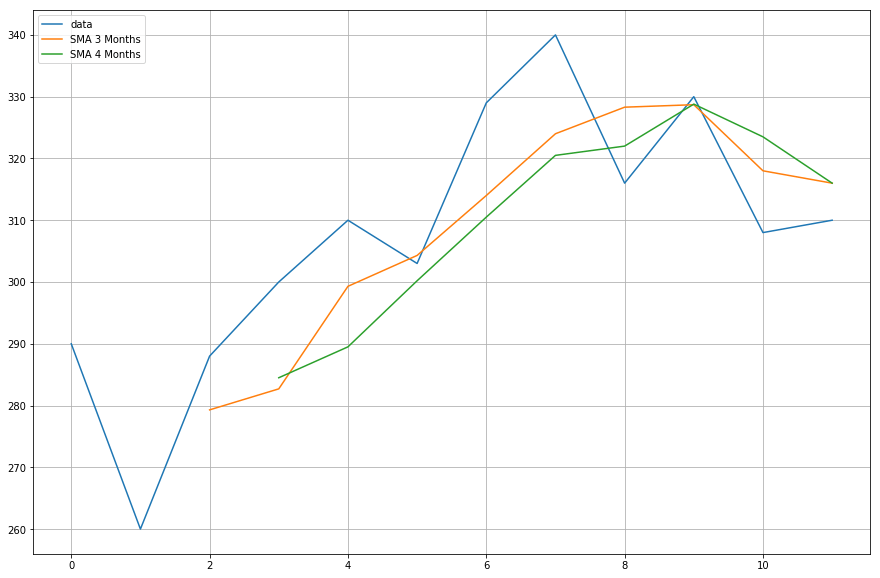
Kumulativer gleitender Durchschnitt
Ich denke, wir sind jetzt bereit, zu einem echten Datensatz überzugehen.
Für den kumulativen gleitenden Durchschnitt verwenden wir einen air quality dataset, der unter diesem Link heruntergeladen werden kann.
df = pd.read_csv("AirQualityUCI/AirQualityUCI.csv", sep = ";", decimal = ",")df = df.ilocdf.head()| Datum | Zeit | CO(GT) | PT08.S1(CO) | NMHC(GT) | C6H6(GT) | PT08.S2(NMHC) | NOx(GT) | PT08.S3(NOx) | NO2(GT) | PT08.S4(NO2) | PT08.S5(O3) | T | RH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10/03/2004 | 18.00.00 | 2.6 | 1360.0 | 150.0 | 11.9 | 1046.0 | 166.0 | 1056.0 | 113.0 | 1692.0 | 1268.0 | 13.6 | 48.9 |
| 1 | 10/03/2004 | 19.00.00 | 2.0 | 1292.0 | 112.0 | 9.4 | 955.0 | 103.0 | 1174.0 | 92.0 | 1559.0 | 972.0 | 13.3 | 47.7 |
| 2 | 10/03/2004 | 20.00.00 | 2.2 | 1402.0 | 88.0 | 9.0 | 939.0 | 131.0 | 1140.0 | 114.0 | 1555.0 | 1074.0 | 11.9 | 54.0 |
| 3 | 10/03/2004 | 21.00.00 | 2.2 | 1376.0 | 80.0 | 9.2 | 948.0 | 172.0 | 1092.0 | 122.0 | 1584.0 | 1203.0 | 11.0 | 60.0 |
| 4 | 10/03/2004 | 22.00.00 | 1.6 | 1272.0 | 51.0 | 6.5 | 836.0 | 131.0 | 1205.0 | 116.0 | 1490.0 | 1110.0 | 11.2 | 59.6 |
Die Vorverarbeitung ist ein wesentlicher Schritt, wenn man mit Daten arbeitet. Bei numerischen Daten besteht einer der häufigsten Vorverarbeitungsschritte darin, nach NaN (Null)-Werten zu suchen. Wenn es NaN-Werte gibt, können Sie diese entweder durch 0 oder den Durchschnitt oder vorhergehende oder nachfolgende Werte ersetzen oder sie sogar weglassen. Obwohl das Ersetzen normalerweise die bessere Wahl ist als das Weglassen, da dieser Datensatz nur wenige NULL-Werte hat, wird das Weglassen die Kontinuität der Reihe nicht beeinträchtigen.
df.isna().sum()Date 114Time 114CO(GT) 114PT08.S1(CO) 114NMHC(GT) 114C6H6(GT) 114PT08.S2(NMHC) 114NOx(GT) 114PT08.S3(NOx) 114NO2(GT) 114PT08.S4(NO2) 114PT08.S5(O3) 114T 114RH 114dtype: int64Aus der obigen Ausgabe können Sie ersehen, dass es etwa 114 NaN-Werte in allen Spalten gibt, Sie werden jedoch feststellen, dass sie alle am Ende der Zeitreihe stehen, also lassen wir sie schnell weg.
df.dropna(inplace=True)df.isna().sum()Date 0Time 0CO(GT) 0PT08.S1(CO) 0NMHC(GT) 0C6H6(GT) 0PT08.S2(NMHC) 0NOx(GT) 0PT08.S3(NOx) 0NO2(GT) 0PT08.S4(NO2) 0PT08.S5(O3) 0T 0RH 0dtype: int64Sie werden den kumulativen gleitenden Durchschnitt auf Temperature column (T) anwenden, also lassen Sie uns diese Spalte schnell von den gesamten Daten trennen.
df_T = pd.DataFrame(df.iloc)df_T.head()
Nun, werden Sie die Pandas expanding-Methode verwenden, um den kumulativen Durchschnitt der obigen Daten zu finden. Wenn Sie sich an die Einführung erinnern, berücksichtigt der kumulative gleitende Durchschnitt im Gegensatz zum einfachen gleitenden Durchschnitt alle vorhergehenden Werte bei der Berechnung des Durchschnitts.
df_T = df_T.expanding(min_periods=4).mean()df_T.head(10)| T | CMA_4 | |
|---|---|---|
| 0 | 13.6 | NaN |
| 1 | 13.3 | NaN |
| 2 | 11.9 | NaN |
| 3 | 11.0 | 12.450000 |
| 4 | 11.2 | 12.200000 |
| 5 | 11.2 | 12.033333 |
| 6 | 11.3 | 11.928571 |
| 7 | 10.7 | 11.775000 |
| 8 | 10.7 | 11.655556 |
| 9 | 10.3 | 11.520000 |
Zeitreihendaten werden in Bezug auf die Zeit gezeichnet, also kombinieren wir die Datums- und Zeitspalte und wandeln sie in ein datetime-Objekt um. Um dies zu erreichen, verwenden Sie das datetime Modul von Python (Quelle: Time Series Tutorial).
import datetimedf = (df.Date) + ' ' + (df.Time)df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))Lassen Sie uns den Index des temperature Datenrahmens mit datetime ändern.
df_T.index = df.DateTimeLassen Sie uns nun die aktuelle Temperatur und den kumulativen gleitenden Durchschnitt im Verhältnis zur Zeit darstellen.
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.legend(loc=2)<matplotlib.legend.Legend at 0x1210a2d30>
Exponentieller gleitender Durchschnitt
df_T = df_T.iloc.ewm(span=40,adjust=False).mean()df_T.head()| T | CMA_4 | EMA | |
|---|---|---|---|
| DateTime | |||
| 2004-03-10 18:00:00 | 13.6 | NaN | 13.600000 |
| 2004-03-10 19:00:00 | 13.3 | NaN | 13.585366 |
| 2004-03-10 20:00:00 | 11.9 | NaN | 13.503153 |
| 2004-03-10 21:00:00 | 11.0 | 12.45 | 13.381048 |
| 2004-03-10 22:00:00 | 11.2 | 12.20 | 13.274655 |
plt.figure(figsize=)plt.grid(True)plt.plot(df_T,label='temperature')plt.plot(df_T,label='CMA_4')plt.plot(df_T,label='EMA')plt.legend(loc=2)<matplotlib.legend.Legend at 0x14b2a41d0>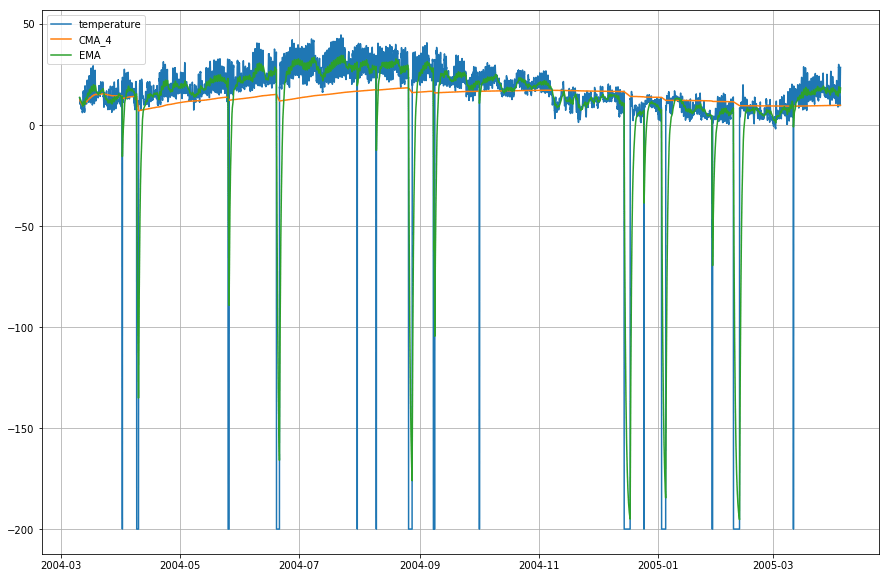
Wow! Wie du also aus dem obigen Diagramm ersehen kannst, leistet Exponential Moving Average (EMA) hervorragende Arbeit bei der Erfassung des Musters der Daten, während Cumulative Moving Average (CMA) bei weitem nicht so gut abschneidet.
Geh weiter!
Glückwunsch zum Abschluss des Tutorials.
Dieses Tutorial war ein guter Ausgangspunkt dafür, wie Sie die gleitenden Durchschnitte Ihrer Daten berechnen und sinnvoll nutzen können.
Versuchen Sie, den Python-Code für den kumulativen und exponentiellen gleitenden Durchschnitt zu schreiben, ohne die Pandas-Bibliothek zu verwenden. Das wird Ihnen ein viel tieferes Wissen darüber vermitteln, wie sie berechnet werden und worin sie sich voneinander unterscheiden.
Es gibt noch viel zu experimentieren. Versuchen Sie, die partielle Autokorrelation zwischen den Eingabedaten und dem gleitenden Durchschnitt zu berechnen, und versuchen Sie, eine Beziehung zwischen den beiden zu finden.
Wenn Sie mehr über DataFrames in pandas erfahren möchten, besuchen Sie den interaktiven Kurs pandas Foundations von DataCamp.